泰勒公式在求解比较大小选择题中的应用
李素馨 冯硕文
湖北大学数学与统计学学院
比较大小的选择题是近年高考的常见题型,一般情况下我们会构造函数模型代入数值进行比较和运算,但是对学生来说函数模型的选择是非常有难度的,因此在选择题中我们可以选择利用泰勒公式计算近似值的办法进行比较大小.
1 泰勒公式在教材中的体现
在人教A版必修一教材(2019年)中三角函数一章第256页“拓广探索”中新增以下第26题.
英国数学家泰勒发现了如下公式:
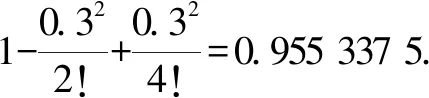
解:经计算得cos 0.3≈0.999 987 2,与由泰勒公式计算所得结果前三项误差不超过0.05.
由教材的例子可以看出,泰勒公式在求实际数值的时候很方便,并且项数比较少的时候就可以达到比较高的精确度.
《普通高中数学课程标准》中明确要求了学生应当在现实问题中,能利用函数模型解决问题.在实际问题中,利用一些重要常数,例如e,π的近似值,对无理数进行比较一直都是非常常见的一类问题.
2 泰勒公式的一般形式
如果函数f(x)在[a,b)上存在直至n阶连续导函数,在[a,b)内存在(n+1)阶导函数,则对于给定的x0,x0∈[a,b),至少存在ξ∈[a,b)使得
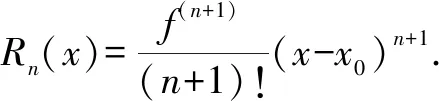
下面给出高中阶段常用的泰勒公式:
3 泰勒公式在求解高考试题中的应用
公式常用于计算近似值,因此对求解比较大小的试题可以简化运算,提高解题效率,现举例说明.
首先来看泰勒公式在求解高考题中的运用,这里只给出泰勒公式解法.
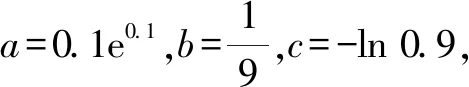
A.a C.c 解:使用泰勒公式 因为 所以c 故选:C. A.c>b>aB.b>a>c C.a>b>cD.a>c>b 解:由泰勒展开式(3),放缩可得 所以b>a.由泰勒展开式(2),放缩可得 综上,c>b>a. 故选:A. A.a C.b 解:由泰勒公式,可知 将x=0.01,x=0.02,x=0.04,分别相应代入估算,得a≈0.019 90,b≈0.019 802,c≈0.019 804. 由此可知b 故选:B 评析:通过以上示例可以看出,利用泰勒公式近似计算求解难度比较大的试题确实可以提高解题速度,但运用该法的难点是要利用数字特征构造对应的函数.其次,在比较大小的解答题中也可以利用泰勒公式,举例如下. 设f(x)=(2.1-2x)ex. ≈2.1+2.1x+1.05x2-2x-2x2-x3. 即f(x)≈2.1+x(0.1-0.95x-x2). 又a>c>1,b<1,则a>c>b.故b 评析:本例中在构造函数时注意尽量不要除式,而是用乘积构造函数,并且注意运用适当的放缩. (1)引入泰勒公式,进行估计 由以上例子可以观之,在高中实际教学中教师可以借助课后习题引入一些泰勒公式的知识,让学生了解一些估计与近似问题若用泰勒公式则会很方便,并且能够通过对一些函数计算具体值的方法进行研究和把握. (2)运用泰勒公式,简化计算 由以上例子也可以看出,泰勒公式在小范围内估值时会非常准确,因此在碰到此类问题时往往可以考虑泰勒公式. (3)深度思考,激发兴趣 教师可以利用“泰勒公式简化计算”这个例子激发学生对数学这门学科的深度思考,引起学生探索数学的兴趣.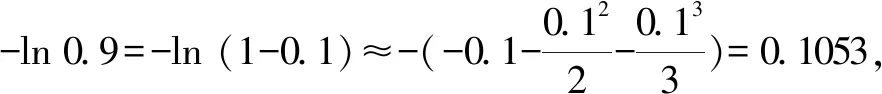
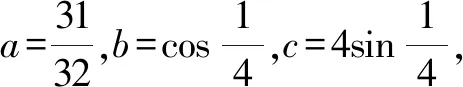
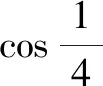
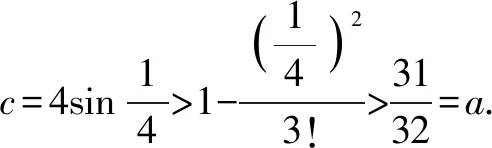
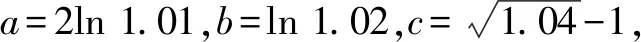

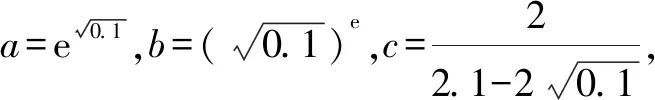
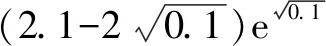


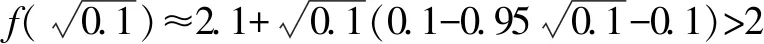
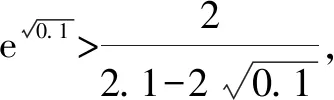
4 教学启示

