风电场理论发电量快速估算模型研究

施 晨，彭秀芳，项 雯，冯 浩，吴浙攀

(中国能源建设集团江苏省电力设计院有限公司，江苏 南京 211102)

0 引 言

“双碳”背景下，风电作为构建新型电力系统[1-3]所必不可缺的能源供给方式而前景光明。随着能源转型，传统能源建设单位涌入风电领域，行业竞争空前激烈，快速获取区域风电投资价值可让建设单位迅速做出投资决策，从而抢占先机。

作为计算投资收益率的关键输入参数，风电场发电量计算在传统风资源评估中依赖软件计算，如代元军等[4]提出了利用WAsP软件求解风力机发电量的方法；周强等[5]运用WT软件计算了华北某风电场区域内风能资源状况；王美琳[6]采用WindSim软件计算了某风电场尾流引起的发电量衰减；许昌等[7-9]基于制动盘理论采用CFD商业软件完成发电量计算基础。这些计算方法建立于成熟的数值模型，需处理测风数据等完整资料，在软件中进行模拟，得出理论发电量后扣除折减得到上网电量。完成全套流程需消耗大量计算资源及时间，且大部分集中在理论发电量计算环节。显然，以上方法在缺乏基础资料的快速决策阶段难以推广运用。

本文首先基于风电场威布尔分布形状和尺度参数，拟合计算测风年各风速段分布频率，将各风速段与优化后的简化功率曲线叠加之后求和，得到风电场理论发电量，形成风电场理论发电量快速估算模型，为风电场快速投资决策形成参考。

1 理论发电量估算模型

1.1 威布尔分布函数

研究表明[10-12]，风速具有统计特征，双参数威布尔分布曲线被认为是能准确描述风速特征的函数，并且威布尔分布概率模型已广泛应用在风电规划设计等环节。其概率密度函数为

(1)

式中，k为威布尔形状参数；c为威布尔尺度参数；w为风速。对式(1)取积分运算，得到威布尔概率分布函数

(2)

在式(2)的基础上，可得到风速段Δw对应的风速频率

(3)

式中，Δw=w2-w1。威布尔分布尺度与形状参数可参考周边风电场或通过公开网站获取。在此基础上可快速得到区域风速频率分布。

1.2 功率曲线模型

风电机组的功率曲线为风电机组输出功率随风速变化的曲线[13]，在风电场建设的前期，由于缺少运行数据，通常采用设备制造商在特定工况下测试得到的标准功率曲线[14]计算风电场发电量。典型风电机组标准功率曲线如图1所示。

图1 某机型标准功率曲线

在风电场快速投资决策阶段，通常缺乏机型功率曲线，因此可借助简化功率曲线模型来模拟风电机组输出功率。常见的简化输出功率模型主要包括线性模型、二次方模型、三次方模型等[15]，简化公式见式(4)～(6)。

(4)

(5)

(6)

式中，Pr为额定功率；Vc为切入风速；Vr为额定风速；Vt为切出风速；a1、b1、a2、b2、c2、a3、b3等系数可通过已知参数求取。

1.3 理论年上网电量模型

基于上述威布尔分布函数及功率曲线模型，得到风电场理论年上网电量Eth

(7)

式中，ρ为项目空气密度；ρ0为标准空气密度；H为测风年小时数；Δwi为第i个风速段。当风速段间隔为km/s时，风速段Δwi表示的风速区间为[wi-0.5k，wi+0.5k)。

2 功率曲线二次方模型优化

2.1 已有模型对比

为探究简化功率曲线的实用性，以图1中的标准功率曲线为基础，分别绘制线性模型、二次方模型、三次方模型曲线，如图2所示。

图2 某机型标准功率曲线与简化模型对比

由图2可知，简化模型在切入风速和切出风速之间的非线性区域，与标准模型相差较大。同时，国内风电场大部分发电量产自额定功率以下，因此切入风速与切出风速之间的非线性区域的准确性与理论发电量的计算关系密切。

以某苏北平原地区风电场为例，分别采用该机型3种简化功率曲线模型叠加威布尔分布进行理论发电量计算并与软件模拟结果对比，如表1所示。

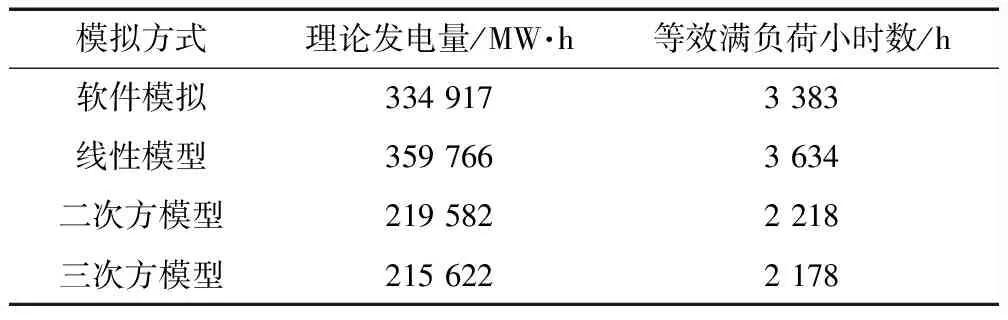
表1 软件模拟结果与简化方法估算发电量对比

可见，二次方模型与三次方模型估算得到的理论发电量均远低于数值模拟结果，而线性模型估算值与软件模拟结果接近且略高，相对偏差仍大于5%。在已知风电场平均风速约5.5 m/s的情况下，结合图2可知：二次方模型与三次方模型在风电机组非额定工况下出力线远低于标准工况，因此无法直接使用；线性模型在非额定功率区间内将功率曲线简化成与标准功率曲线有唯一交点的线段，由于其风速频率大部分处于交点以左的区间且该区间功率值均大于标准功率值，因此最终发电量略高于模拟值。

进一步分析可知，随着机组单机容量的变化，线性功率曲线与标准功率曲线的交点位置变化较大，引起发电量偏差的随机性，因此难以在发电量快速计算模型中应用；同时发现，通过更改二次方模型参数点的位置优化抛物线形状，可以达到应用于快速计算发电量的要求，因此本文针对二次方模型进行优化。

2.2 模型优化

基于上述模型分析，对二次方模型进行优化。结合式(5)可知，二次方模型在非额定功率曲线上的方程共需求解a2、b2、c2等3个参数值，根据二次方功率曲线特性，3个参数值可通过求解式(7)得到[15]

(8)

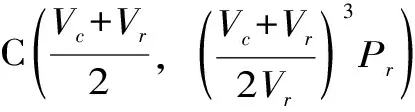
表2 代表性机型计算功率与标准功率对比

(9)

可得

(10)

式(10)给出了二次方功率曲线优化模型参数a2、b2、c2与Vc、Vr关系式，可根据式(10)求取二次方功率曲线模型关系式。

3 算例分析

3.1 计算过程及结果

以本文第二节中的风电场为例，采用威布尔分布叠加二次方功率曲线优化模型的方式，计算理论发电量。

根据风电场威布尔分布参数，结合式(3)，计算得到不同风速段的风速频率以及对应的风速小时数分布。结合风电场设计机型的各临界风速参数，采用优化后的二次方功率曲线模型，得到风电场功率曲线快速计算公式

(11)

计算得到风电场平均单台机组理论年发电量为10 925.90 MW·h，全场理论年发电量1 042 460.1 MW·h，等效满负荷小时数约为3 311 h。

针对单机容量分布在2.5～5.0 MW之间的5座典型风电场，采用上述计算流程计算各风电场理论年发电量等效满负荷小时数，见表3。

表3 典型风电场理论年发电量估算

3.2 误差分析

为验证快速计算模型可靠性，对计算结果进行误差分析。风电场在设计阶段计算收益率时，通常以数值计算软件模拟得到发电量作为输入参数。因此，本文采用数值模拟软件Meteodyn_WT模拟得到的理论发电量作为参照对象。

以表3中单机容量4.0 MW的风电场为例，采用数值软件计算理论发电量。该项目地形文件根据公开的SRTM地形图高程数据生成等高线，粗糙度文件根据天地图显示的地貌特征绘制粗糙度线并赋值。

计算绘图区域为风电场及外扩约5 km的范围，步长设置为50。最小水平与垂直分辨率分别设置为25和4，热稳定度为中性，扇区步长为22.5°。风机尾流模型为PARK模型，湍流模型采用完整的Frandsen模型。风电场区域140 m高度风功率密度模拟云图如图3所示。

图3 风电场140 m高度平均风功率密度云图

经过计算，软件模拟理论发电量等效满负荷小时数为4 048 h。采用上述方法计算表3所列7个风电场模拟理论发电量，并与快速估算方法计算的理论发电量进行对比，见表4。

根据表4，7座典型风电场快速估算理论发电量等效满负荷小时数与软件模拟值最大差值143 h，最小差值2 h；最大相对偏差4.35%，最小相对偏差0.06%；平均差值60.7 h，平均相对偏差1.89%。最大与平均相对偏差均在5%以内，相对偏差较小。在进一步计算上网电量时，通常需要考虑约5%～10%的尾流折减以及75%～80%的风电场年上网电量修正，叠加上述折减后得到的上网电量，平均差值可进一步下降至41.0～46.1 h，误差程度在快速决策阶段处于可接受范围内。

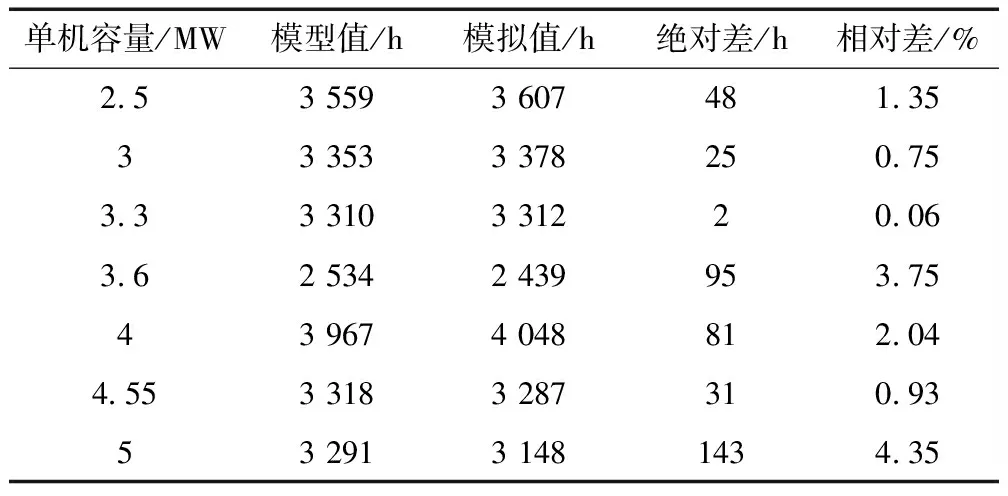
表4 计算值与模拟值对比

4 结 论

本文优化了二次方功率曲线模型，在此基础上结合威布尔分布函数建立风电场理论年发电量快速估算模型。进一步进行了模型验证与误差分析，结果表明：快速估算模型计算理论发电量与软件模拟结果相对偏差低于5%，在叠加修正后，偏差可进一步降低，表明该模型在快速决策阶段具有一定的可行性。