基于机器学习性能度量理论的保障资源指标综合权衡研究

甘娥忠，刘 焱，王海荣，王承光

（四川航天系统工程研究所，四川 成都 610100）

0 引 言

随着装备复杂程度日益增加，用户对通用质量特性要求也逐渐增多，各种指标之间存在不协调的情况时有发生。保障资源指标也面临相同问题，在进行保障资源指标论证时，指标制定过多、过少、过高或过低都会导致装备战斗力的丧失或保障资源的浪费。为了保证整个研制过程及保障过程按优化方向发展，需在装备论证阶段对保障资源指标进行择优和权衡。

虽然指标论证对综合权衡具有重要需求，但由于数据缺失及权衡方法的局限性，导致综合权衡得出的指标难以有效影响指标论证，造成目前装备的保障资源指标论证基本上依靠参考同类型产品的局面。

2009 年GJB 1909A［1］提出了用综合权衡的方法确定保障资源指标，给出了飞机、舰船等装备的备件利用率和备件满足率的定义及计算公式，其中备件利用率可以从经济效率的角度来衡量备件是否“物尽其用”，而备件满足率则可以从军事效益角度来衡量备件供应是否到位，进而评价战备完好性，备件利用率和备件满足率这一对参数有效地支撑了相关装备的指标论证。但针对备件满足率与备件利用率的相互制约特性，如何采取综合权衡的方法确定出科学合理的结果，成为工程实践的难题。

2015 年，应新雅等［2］结合随舰备件配置问题，建立了备件利用率的概率模型，揭示了备件利用率的内涵和实际工程意义，在此基础上，建立以系统备件满足率为约束、备件利用率为优化目标的配置方案优化模型；2016 年，李华等［3］针对保障概率这个目标优化问题，提出将备件利用率也作为评价指标，提出了备件利用率的评估方法；2022 年，王俊龙等［4］建立了通用件的备件满足率和备件利用率评估模型，通过算例分析了常用备件评估指标备件满足率和备件利用率之间的关系。上述几篇文章对备件利用率和备件满足率均开展了理论分析，但对综合权衡问题都是浅尝辄止，未介绍具体方法。如何确定合理的指标，既保证装备维修的需要又满足经济性原则，是本文研究的主要目标。

本文以现场可更换单元（line replaceable unit，LRU）的备件需求量预测模型为基础，通过理论分析和推导，提出典型条件下的备件满足率和备件利用率权衡模型，为基于备件需求量预测的指标权衡模型提供了一套快速简单且实用的理论方法。

1 模型假设

为了明确问题，特限定模型的适用范围，做出如下假设：① 考虑LRU种类单一的系统；② 考虑初始备件配置；③ LRU 分类为关键件、重要件及一般件；④ LRU 失效立即进行备件更换；⑤ 备件失效概率服从特定分布；⑥ 不考虑备件更换的时间及等待时间；⑦ 不考虑备件的失效和退化；⑧ 不考虑备件空间的约束。

2 备件利用率与备件满足率

在实际备件配置过程中，根据备件需求和配置情况的组合，备件可以划分为4 种类型，包括：需求且已配置（记为TP）、无需求而配置（记为FP）、需求而未配置（记为FN）及无需求且未配置（记为TN）。令TP、FP、FN、TN分别代表这4 种类型备件对应的个数，显然TP+FP=配置的备件数量，TP+FN=需求的备件数量［2］。分类结果可以借用机器学习领域的混淆矩阵方式进行呈现，见表1。

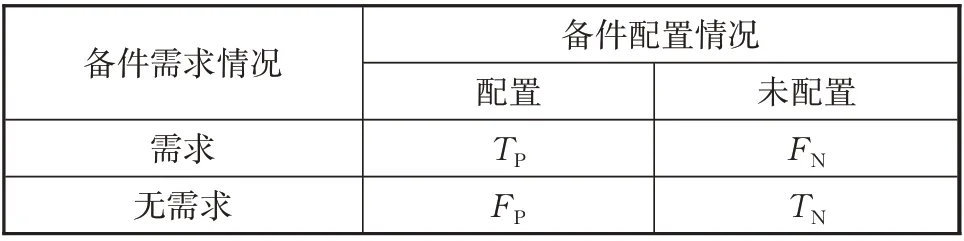
表1 备件分类混淆矩阵Tab.1 Spare parts classification confusion matrix

参考GJB 1909A—2009《装备可靠性维修性保障性要求论证》，备件利用率（标记为P）的定义为“实际用到的备件数量和配置的备件数量之比”，即

备件满足率（标记为R）的定义为“能提供的备件数量和需要的备件数量之比”，得出

考虑备件需求量和备件配置量是两个互不相关的离散型随机变量，可以将备件需求量标记为随机变量i，备件配置量标记为随机变量j，有i，j∈N。根据式（1）和（2）可知，P和R是和备件需求量i及备件配置量j相关的随机函数。我们定义Pij为备件需求量为i、备件配置量为j时的备件利用率，同理Rij为备件需求量为i、备件配置量为j时的备件满足率，结合表1提供的混淆矩阵进行分析，可得分段函数［5］

可以看出Pij≤1、Rij≤1，且当i=j时Pij=Rij=1。为了方便矩阵计算，根据式（3）和（4），备件利用率与备件满足率的随机函数可以用高阶混淆矩阵的方式来表示，见表2和表3。

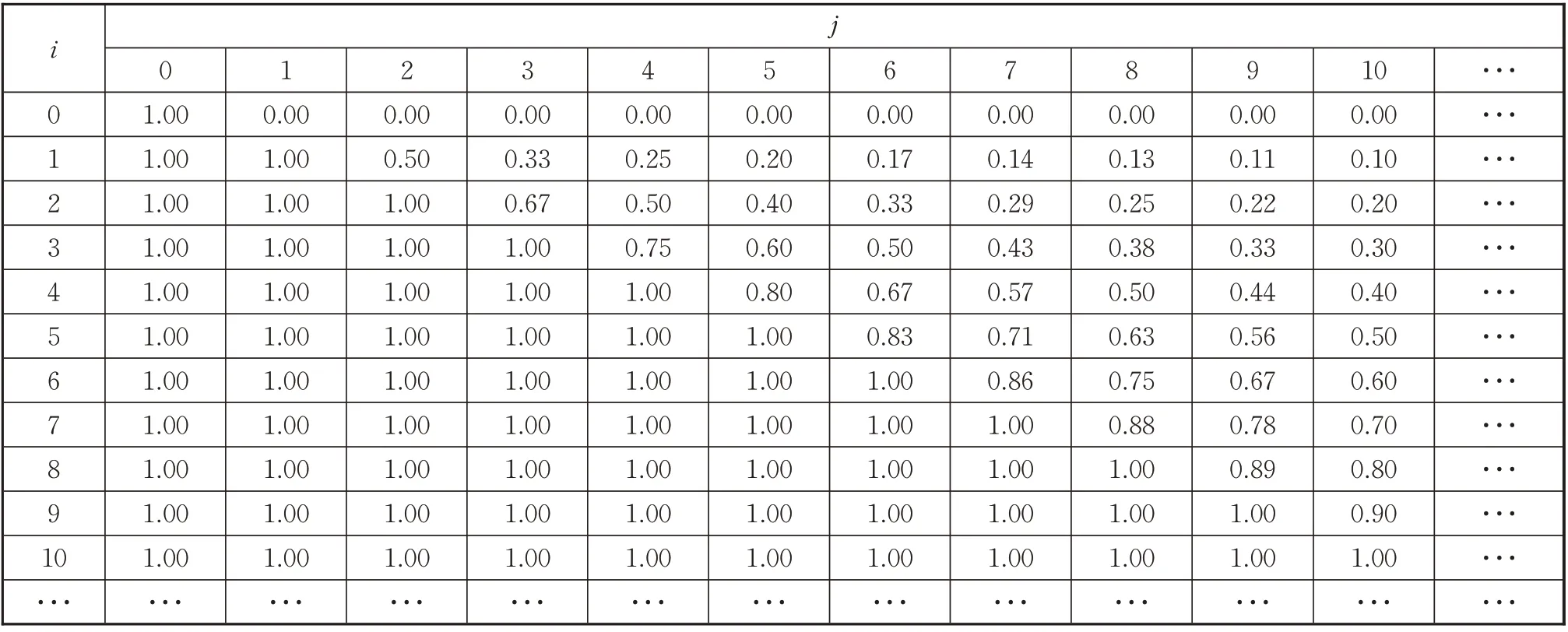
表2 备件利用率的高阶混淆矩阵PTab.2 High-order confusion matrix P of spare parts utilization rate

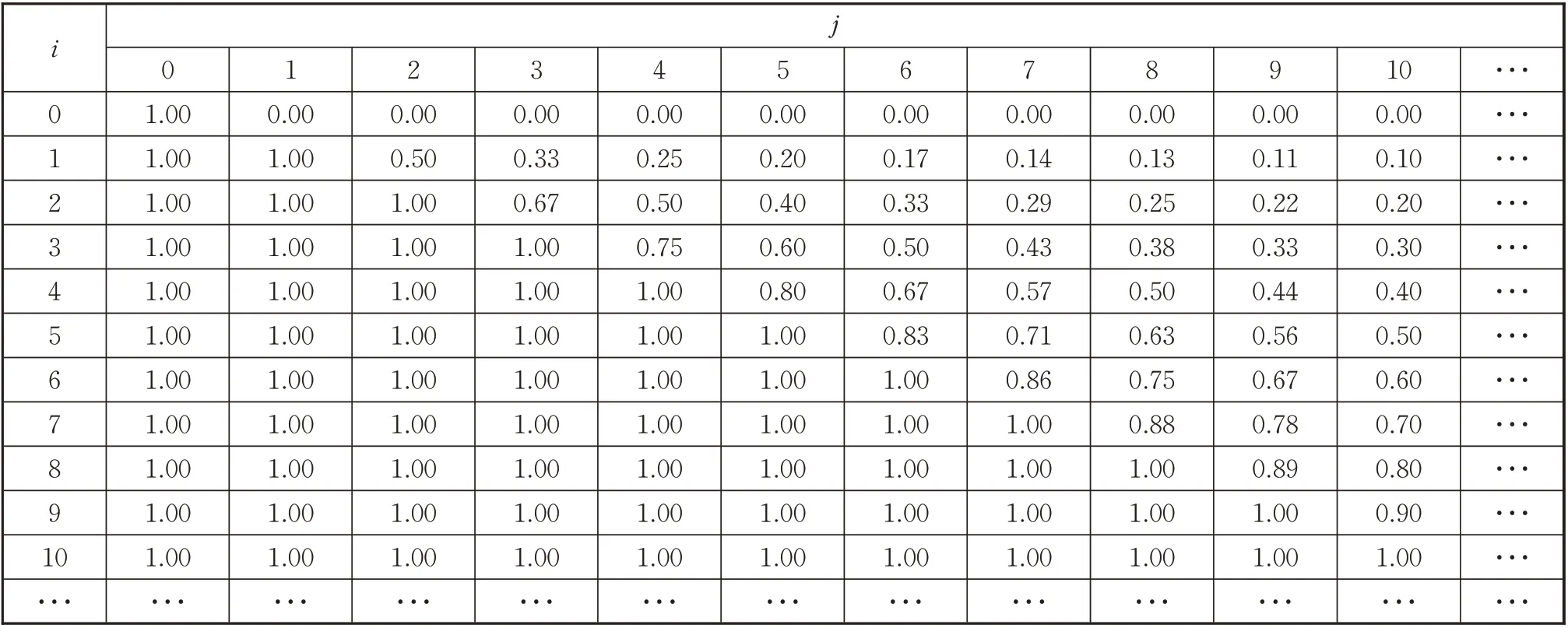
表3 备件满足率的高阶混淆矩阵RTab.3 High-order confusion matrix R of spare parts satisfaction rate

3 备件需求量预测

备件需求量是一个随机变量，且与装备的任务时间、使用强度、使用环境、装备中同种类型可更换单元数量等因素有密切关系，因此备件需求量预测的研究成果也异常丰富。

综合来看，备件需求量的预测理论大致可以分为3 类［6］：第一类是以时间序列为基础进行的预测，主要用到的方法包括指数平滑法、马尔科夫链预测模型［7］等；第二类是以机器学习理论为基础进行的预测，包括大量的支持向量机回归预测［8］、人工神经网络［9］等人工智能算法；第三类则是以可靠度为基础进行预测，当制定推荐配置备件清单（recommended spare parts list，RSPL）或历史保障数据不足时，常常会用到该方法。

为了便于理解，本文以第三种方法为例，假设失效的单元都可以即时更换，此时，备件需求量即等于任务时间内失效单元个数，而可更换单元的失效可以借助泊松分布来计算［10］。更一般地，假设装备中有某同种类型单元N个，且各单元服从指数分布，失效率均为λ，时间间隔为t，根据平均失效率的定义，可知

式中：ΔN表示时间t内的失效个数的期望，带入泊松分布公式可以计算出在t时间内发生k次失效的概率为

4 综合权衡方法

按照LRU 对整个装备功能的影响程度，LRU 可以分为关键件、重要件和一般件3种。关键性越高，表明其对装备系统的影响越大，该类LRU对备件的需求也越大。因此，关键件，通常考虑其军事效益，需要将备件满足率指标作为硬性指标；一般件，其失效不会对人员安全和装备任务的执行产生很大影响，为了考虑其经济效益，需要将备件利用率指标作为主要参考指标；重要件，则需要综合权衡效果和经济两种因素，既保证装备维修的需要，又满足经济性原则［11］，这也是综合权衡的主要研究对象。

利用式（6）或其他预测模型，可以得到LRU 备件需求量的概率分布p(k)，再结合备件利用率和备件满足率的高阶混合矩阵P和R，可以算出备件配置量为j条件下的备件利用率期望Pj与备件满足率期望Rj分别为

式中：K为t时间内单元失效个数的极大值。

Pj和Rj是关于备件配置量j的随机向量。为了直观地显示备件利用率与备件满足率的制约关系，可以引入机器学习领域的“P-R曲线”［12］的概念，利用不同备件配置量条件下的Pj和Rj进行描点，以备件满足率R为横坐标、备件利用率P为纵坐标作图，即得到了备件利用率-备件满足率曲线，简称“P-R曲线”，“P-R曲线”的一般示意图如图1 所示。由图1 可知，“P-R曲线”为单调减函数，且在极限条件下，当备件满足率为0 时，备件利用率为1；当备件满足率为1 时，备件利用率为0。

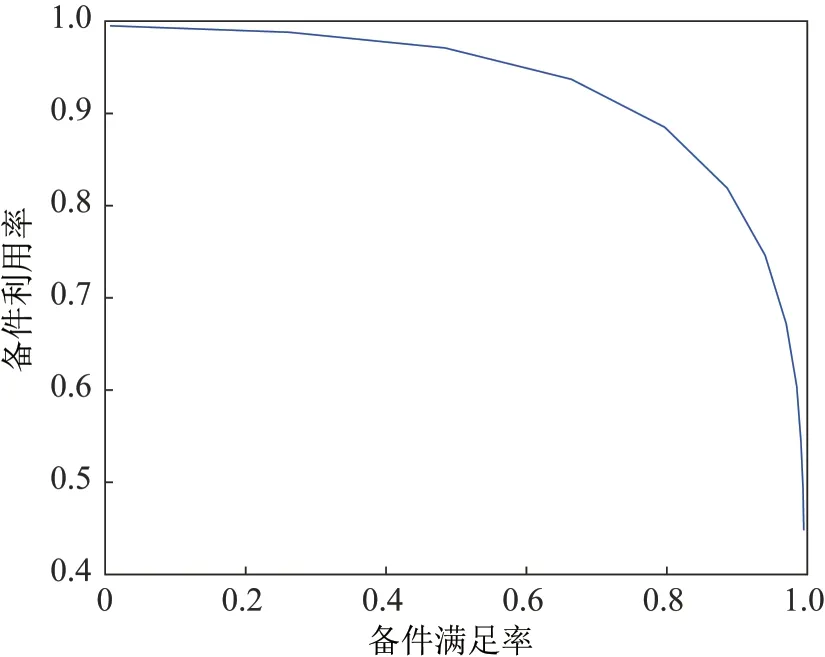
图1 “P-R曲线”示意图Fig.1 Diagram of “P-R curve”

对于关键件和一般件的指标权衡，处理非常简单，直接利用“P-R曲线”的单调性，只需考虑在最小满足备件满足率或备件利用率的情况下，即可确定出对应最大的备件利用率和备件满足率。

本文针对重要件，借鉴机器学习方法中的性能度量理论［13-14］，选出3种综合度量方法，对备件利用率和备件满足率的指标进行综合权衡，确定最合适的保障资源指标。

4.1 “平衡点”法

“平衡点”（break-even point，BEP）顾名思义是“备件利用率=备件满足率”时的取值，可以进行备件利用率和备件满足率同等重要条件下的初步权衡，根据图1，可以通过插值的方法很直观地计算出实际案例中的BEP，具体示意图如图2所示。

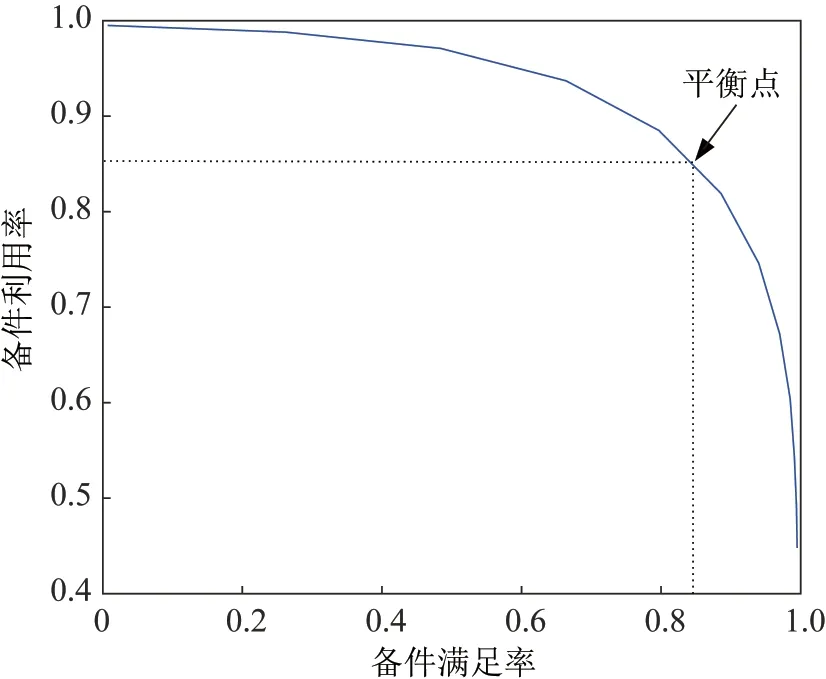
图2 BEP及最优指标示意图Fig.2 Diagram of BEP and the optimal indicators

考虑到在平衡点处备件配置量可能不为整数，从实际出发，可以将平衡点处备件配置量相邻的备件配置量作为备选方案，再根据备件利用率和备件满足率的重视程度，选择左偏或右偏。

另外，“平衡点”法主要目的不是用来做指标的综合权衡，而是用来对不同装备之间的可保障性水平进行比较，BEP越大说明装备的可保障性越好。

4.2 F1度量

和平衡点法的感性判断不同，F1度量借用调和平均的概念，对“P-R曲线”上的每个点进行量化度量，F1度量计算式为

根据F1函数可以计算出F1最大值，此时的j则为最佳的备件配置量，而Pj和Rj即为最合适的备件利用率和备件满足率指标，F1度量提供了两个及两个以上矛盾参数同等重要条件下的度量方法。

4.3 Fβ度量

Fβ度量［15］是F1度量的一般形式。对于备件利用率和备件满足率有明显的偏好，但又达不到关键件或一般件的程度时，可以通过Fβ度量进行权衡，计算式为

随着对两个指标的重视程度更加细化，可以形成高阶代价矩阵［14］，对不同指标下的代价进行期望计算，得到更精确的衡量结果，本文对此不做详细演算。

4.4 适用情形

上述各种方法提供了综合权衡的工程化思路，不同方法适用的情形根据备件的重视程度各不相同，因此得到适用情形分类表见表4。

表4 不同权衡方法适用情形分类表Tab.4 Classification of different trade-off methods applicable to cases

5 案例分析

5.1 模型求解

假设某论证案例［10］：某雷达装备具有同型可更换单元5个，可更换单元的失效率λ为10-4次/h，在2年保障时间内，每年累计工作时间5 000 h，若可更换单元的部分失效不会导致装备性能的完全消失，如何确定该型可更换单元保障资源指标。

考虑到该可更换单元的部分失效仅会导致装备性能的部分下降，则该可更换单元可以认定为重要件。假设保障期内备件的失效和退化忽略不计，考虑到可更换单元的寿命分布服从指数分布，在寿命周期内的失效率为常数，可更换单元在单位时间内失效的个数服从泊松分布，可以算出规定时间内可更换单元的失效概率为

式中：N=5 表示装备中同型可更换单元的个数；λ=10-4次/h 表示可更换单元的失效率；t=2×5 000 h表示装备使用时间；k表示可更换单元失效个数。代入式（11）计算可得该型可更换单元的失效概率分布，见表5。

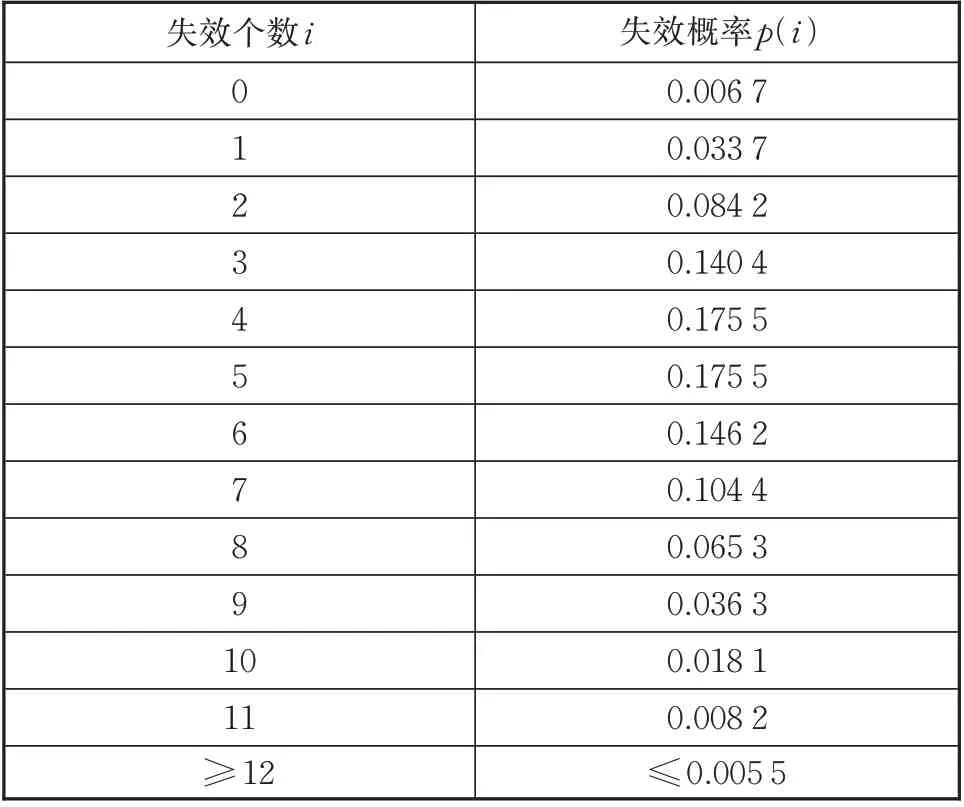
表5 可更换单元失效个数与失效概率的对应关系Tab.5 Correspondence between the number of LRU failures and the failure probability

考虑到失效个数大于等于12 时，失效概率很小，为了便于计算，仅考虑前11 个失效数据，将表5 中的数据代入式（7）和（8），Pj与Rj结果如表6所示。

表6 备件利用率期望Pj与备件满足率期望RjTab.6 Spare parts utilization expectations Pj and spare parts satisfaction rate expectations Rj

备件利用率期望Pj与备件满足率期望Rj与备件配置量的对应关系如图3所示。

从图3可知，备件配置量增加时，备件满足率会逐渐提高，备件利用率将会逐渐下降，符合我们的预期。当增加备件配置量时，所有备件都将配置充足，肯定会有多余的备件剩下，这样备件利用率就会下降；但若只配置最有把握的备件，难免会漏掉不少需求的备件，备件满足率则会降低。

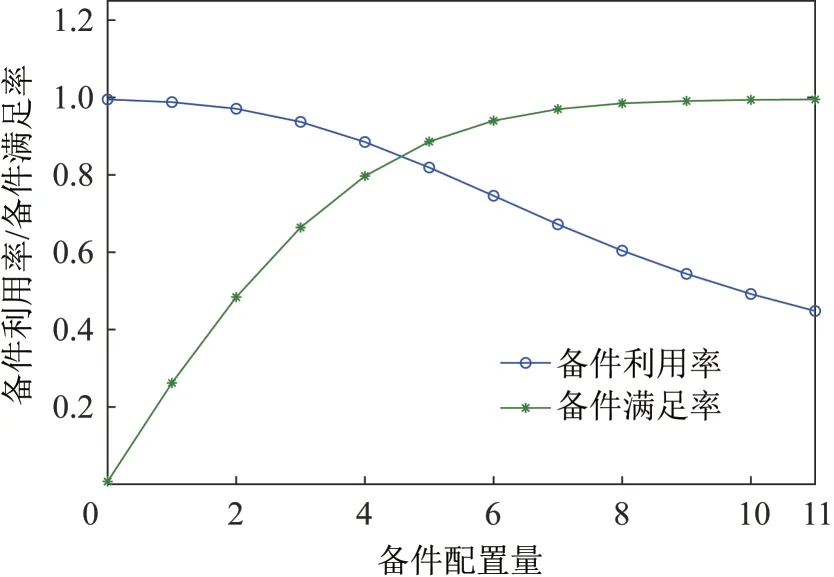
图3 备件利用率及备件满足率与备件配置量的对应关系Fig.3 Correspondence between spare parts utilization rate and spare parts satisfaction rate and spare parts configuration quantity

假设该案例中备件满足率和备件利用率重要性相同，可以采用F1度量的方式进行权衡计算，将表5中的结果代入式（9），绘出对应的F1曲线图并找到对应的F1最大值，如图4所示。

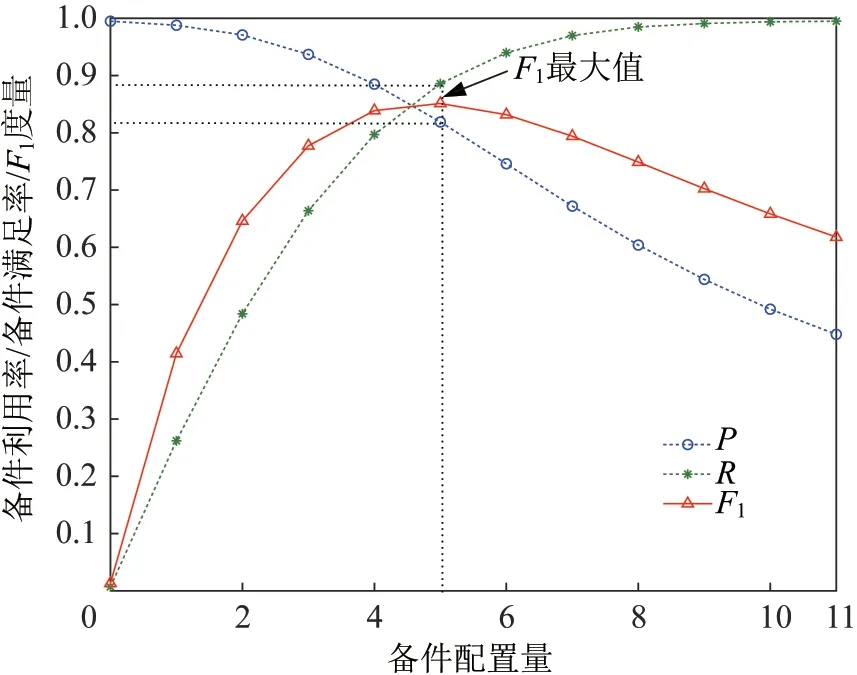
图4 F1度量及最大值示意图Fig.4 Diagram of F1 measure and maximums F1

通过F1度量可以计算出，当备件配置量为5时，F1取得最大值，此时备件利用率为0.819，备件满足率为0.886，据此可以确定出保障资源指标。

5.2 参数分析

装备的保障资源指标和同型可更换单元的个数N、可更换单元的失效率λ、装备使用时间t及备件满足率对备件利用率的相对重要性β都有密切的关系。为了分析出不同参数对保障资源指标的影响，对不同参数条件下的保障资源指标进行比较。

案例中假设备件满足率和备件利用率重要性相同，若假设有三型装备备件满足率对备件利用率的相对重要性β分别取0.5、1.0 和2.0，绘出他们对应的Fβ曲线图及找到对应的Fβ最大值，如图5所示。

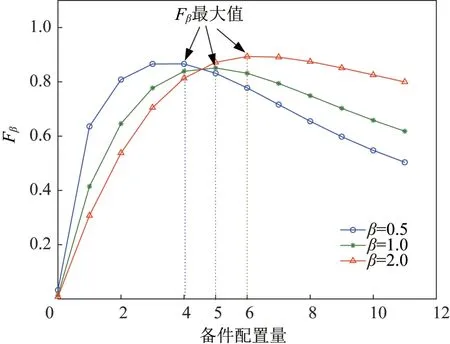
图5 Fβ最大值与β关系图Fig.5 Correspondence between maximumsFβandβ

从图5 可以看出，在一定范围内随着备件满足率重要性β值的增加，相对应的Fβ最大值也逐渐在右移，即最佳备件配置量增加，说明备件满足率指标重要性的增加会导致备件配置量的增加。另外，备件满足率指标重要性越高，其前段上升得越缓、后段下降得也越缓；备件利用率指标重要性越高，其前段上升得越急、后段下降得也越急，说明备件利用率比备件满足率对备件配置量表现更敏感。

另外假设有三型装备，同型可更换单元的个数为分别为6、8 和10，绘出三型装备的“P-R曲线”及对应的BEP，如图6所示。

由图6 可以看出，当同型可更换单元的个数N逐渐增多时，该型装备对应的BEP 会逐渐减小，表明装备的备件利用率及满足率两个指标都在同步减小，说明装备的可保障性在降低，不利于装备的保障。根据式（11），可更换单元的失效率λ及装备使用时间t的增加也会令装备的可保障性下降，该结论为提高装备保障性设计水平提供了参考。

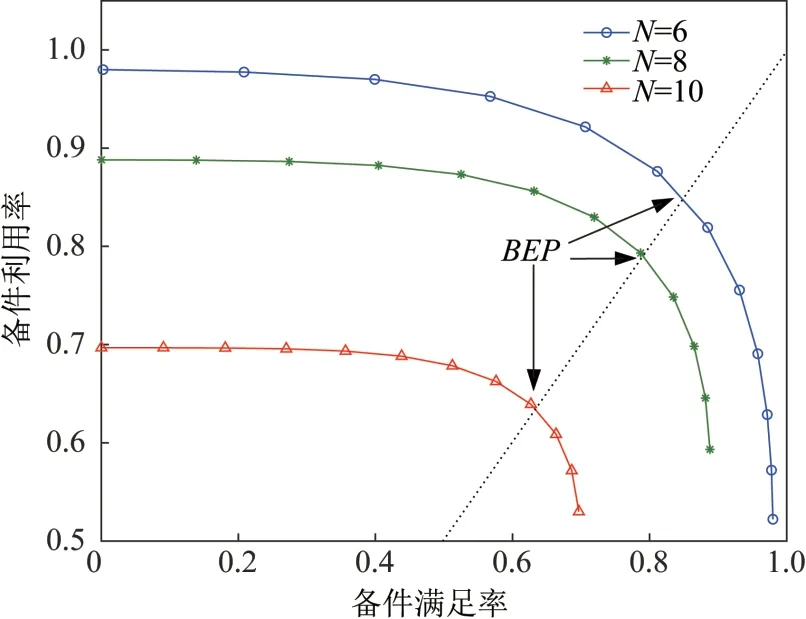
图6 BEP与同型可更换单元的个数N的关系Fig.6 Correspondence between BEP and number of the same type LRU

6 结束语

本文针对保障资源指标综合权衡问题进行了研究，提出了一种便于工程实施的保障资源指标论证方法，具有可迁移性强的特点，为装备的保障资源指标确定及备件的精确保障提供了理论依据。后续将结合多型LRU的问题，开展系统保障资源指标的论证工作，以应对复杂系统的论证需求；结合系统保障资源指标的论证，开展保障资源设计技术研究。