考虑横向转运和紧急配送的战时多目标备件调度方法

李京峰, 陈云翔, 项华春, 高杨军, 赵静

(1. 空军工程大学 装备管理与无人机工程学院，陕西 西安 710051; 2. 西安卫星测控中心 宇航动力学国家重点实验室，陕西 西安 710043)

0 引言

空军战役军团遂行战役任务对飞机备件供应保障的依赖性日益增加。虽然在战役准备阶段，已根据作战方案、预定战场、战役力量等筹措和储备了一定的备件资源，但是由于战役实施阶段战役发展瞬息万变，备件消耗具有高度不确定性，部分作战单位可能在某一时期出现缺件现象，因此能否及时合理地开展战时备件调度将直接影响战役进程和结局。

目前，关于备件调度的研究大多集中在常用的正向调度模型，Sherbrooke[1]、Muckstadt[2]、Graves[3]提出的METRIC 系列模型被认为是处理备件库存问题最早的定量模型，在此基础上，相关领域学者进行了其他扩展。文献[4]研究了供应不足条件下作战资源连续消耗的两级供应系统战场调度问题。文献[5]针对三级供应系统在战时存在供应中断风险的情形，提出战时备件供应的多目标 选址–分配联合优化模型。文献[6]为解决实际备件保障工作中需求以间歇性需求为主的问题，建立了多阶段备件调度模型，利用元启发式动态进化算法进行求解。文献[7]为在多目标备件调度优化结果的非支配解集中选出最优方案，提出一种基于交叉效率排序的多目标进化算法。

当前研究虽然在备件调度方面取得一定成果，但若应用于战时还存在以下现实问题：作战单位在战役实施过程产生的备件需求，往往需要在较短的时限内得到满足，具有很强的时效性。此外，如果后方仓库的备件供应尚未到达，野战仓库则会存在暂时缺货的风险。综上所述，若继续严格按照逐级供应的模式进行备件保障，则会有部分飞机因缺件导致停机等待维修，影响再次投入作战。因此需要打破平时的区域或组织结构限制，考虑将备件从相邻作战单位横向转运，以及从后方仓库直接紧急配送到相关作战单位，提高备件供应的灵活性[8-11]。文献[12]针对单中心仓库两级供应系统的备件调度问题，采用横向转运策略减少平均供应延迟时间。文献[13]针对舰船编队长期远海执行任务中的备件补给难题，依据生灭过程和METRIC 提出一种考虑随机需求的三级备件供应系统横向转运配置优化模型。文献[14]以三站点组成的备件供应保障系统为研究对象，通过引入站点间的供应保障关系建立了三站点备件延期交货量方程组，并基于压缩映射原理给出了求解方法。文献[15]针对备件供应网络结构优化问题，提出一种超启发式多目标进化算法详细对比了传统正向供应网络、应急横向供应网络以及闭环供应网络在备件供应时效性和经济性上的差异。

可以发现，以上研究仅考虑了加入横向转运的单一策略，未将备件调度模型进一步拓展到同时考虑横向转运和紧急配送策略。且上述文献大多针对单种备件开展研究，不同需求点之间缺乏优先度排序，而实际备件调度工作通常涉及多种备件，在仓库备件库存有限的前提下，需要根据需求点紧迫性等多方面因素确定调度优先顺序。另一方面，关于平时备件调度的研究，目标函数大多以经济性为主要依据。战时备件调度则更加强调备件保障程度和时效性，即在缺件数最少的前提下兼顾时间成本最少，属于多目标优化问题。

本文提出一种考虑横向转运和紧急配送的战时多目标备件调度方法。具体方法为：在传统正向调度模型基础上加入横向转运和紧急配送策略，以总缺件数最少和总运输时间最短为目标，构建能够同时处理多类型备件的新型战时备件调度模型；利用逼近理想解排序法(TOPSIS)求取需求点优先度排序，参照基于分解的多目标进化(MOEA/D)算法框架设计考虑优先度排序的MOEA/D(MOEA/D-PS)求解模型；最后，通过案例分析验证本文构建模型的优越性以及MOEA/D-PS 性能，并对需求点优先度排序和要求时限的影响进行分析。

1 问题描述与假设

战役任务实施阶段，根据敌方威胁及空军战役军团飞机备件供应保障特点，备件供应网络分为后方仓库、野战仓库、场站仓库三级，具体如图1 所示。

后方仓库通常距离作战区域较远，备件品种齐全且数量充足；野战仓库设置在作战区域内，负责备件中转和存储，仓库规模介于后方仓库和场站仓库之间；而场站仓库则直接为作战单位飞机的维修保障提供备件，同时是备件需求产生的源头。按照图1(a)传统的正向备件供应网络，飞机备件需严格逐级调度，即先从后方仓库配送至某一作战区域内的野战仓库，再从野战仓库配送至作战单位的场站仓库。然而战时备件需求产生的突发性、数量的不确定性以及调度时间窗口的紧迫性使得正向供应网络适应度变差，容易产生较多缺件被迫停机现象以及较长的运输时间，故需要搭建更加灵活的供应网络以改善战时备件调度模型。图1(b)考虑了横向转运，使得储备同型备件的相邻场站仓库在触发横向转运条件时为缺件单位提供备件；图1(c)则允许在达到越级紧急配送的情况下，从后方仓库直接前运至缺件单位，这两种供应网络虽然在一定程度上能缓解战时备件调度的压力，但与战时调度要求仍有差距。因此本文构建了图1(d)所示的同时考虑横向转运和越级紧急配送两种调度策略的备件供应网络，尝试进一步提升战时备件调度能力。

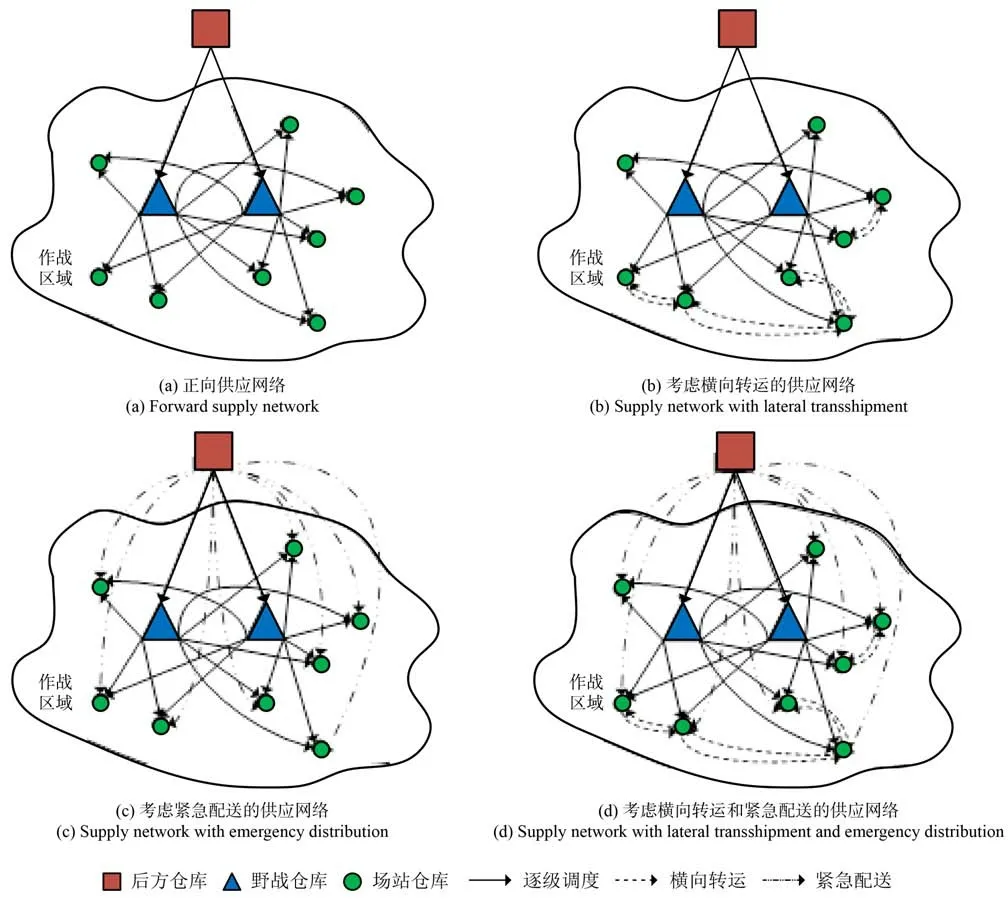
图1 四类备件供应网络Fig. 1 Four types of spare parts supply network

为便于建立战时备件调度模型，本文做出以下假设：

1)研究对象包括多种类型备件需求，假设各类型备件同等重要，忽略备件大小对调度方案生成的影响；

2)各级仓库关于各型备件的库存量已知，各个作战单位关于各型备件的需求量已知；

3)网络节点之间的运输时间已知；

4)不同作战单位关于同型备件的需求存在优先度排序；

5)横向转运比紧急配送更加节省时间，且采取两种策略需满足一定规则：如果按级调度运输时间大于要求时限或者横向转运更加节省时间，或者野战仓库缺货，同时相邻场站有对应库存则采取横向转运。如果野战仓库和相邻场站均无足够备件库存，而节点间紧急配送时间能够满足要求时限，则采取紧急配送，否则造成缺件；

6)横向转运时场站仓库备件完全共享，后方仓库备件充足。

2 模型构建

战时备件调度应在规定时间内最大化满足作战单位备件需求，即要在尽量减少缺件数量的基础上兼顾运输时间，使备件尽早到达作战单位。这是因为飞机上部件出现故障或者战损后会严重影响飞机完成作战任务的完好性要求和持续性要求。因此需要各级仓库在现有库存的基础上按照一定规则合理分配备件资源，优先满足备件需求数量，保证更多飞机能够加入作战任务，其次优化运输时间，提高战时备件调度效率。本文以总缺件数最少为第一目标，以总运输时间最短为 第二目标，建立图1 中4 种备件供应网络分别对应的多目标战时备件调度模型，并在案例分析中将 4 种调度模型的调度效果进行对比。

2.1 符号定义

为便于阅读，模型涉及的所有参数和变量符号如表1 所示。

表1 模型符号描述Table 1 Model notation description

2.2 正向调度模型

目标函数1：战时备件调度的总缺件数最少，即

目标函数2：战时备件调度的总运输时间最短，即

其中，式(3)表示第i个野战仓库的供出量不能超过供入量和库存量之和；式(4)表示第j个场站仓库的供入量和库存量之和不能超过需求总量；式(5)和式(6)表示两种正向调度方法均需满足要求时限；式(7)和式(8)则确保运输量和要求时限非负。

2.3 考虑横向转运的调度模型

目标函数1：战时备件调度的总缺件数最少，即

目标函数2：战时备件调度的总运输时间最短，即

其中，式(12)中第j个场站仓库的供入量在正向供应基础上增加了横向转运项；式(13)规定了二元决策变量在不同条件下的取值。

2.4 考虑紧急配送的调度模型

目标函数1：战时备件调度的总缺件数最少，即

目标函数2：战时备件调度的总运输时间最短，即

其中，式(19)中第j个场站仓库的供入量在正向供应基础上增加了紧急配送项；式(20)规定了二元决策变量在不同条件下的取值。

2.5 考虑横向转运和紧急配送的调度模型

目标函数1：战时备件调度的总缺件数最少，即

目标函数2：战时备件调度的总运输时间最短，即

其中，式(26)中第j个场站仓库的供入量同时增加了横向转运和紧急配送两项。

3 考虑优先度排序的MOEA/D-PS 算法

由于以上构建的战时备件调度模型属于多目标优化问题，且战时的特殊环境要求调度方案必须快速生成，求解算法要兼顾质量和效率。MOEA/D[16]将一个多目标优化问题分解为若干个标量优化子问题，并同时对其进行优化。每个子问题仅利用相邻子问题的信息进行优化，使得MOEA/D 每一代的计算复杂度都比较低，需要较少的计算时间，符合模型求解需要。鉴于此，结合战时备件调度模型特点，本文对MOEA/D 进行改进，提出MOEA/DPS。

MOEA/D-PS 在MOEA/D 框架的基础上增加了对不同作战单位需求的优先度排序算子，以解决战时备件调度面临的资源有限、需求紧急程度不同的供需矛盾。其次，采用模拟二进制交叉(SBX)[17]算子和多项式变异算子进化种群。MOEA/D-PS 算法流程如图2 所示。

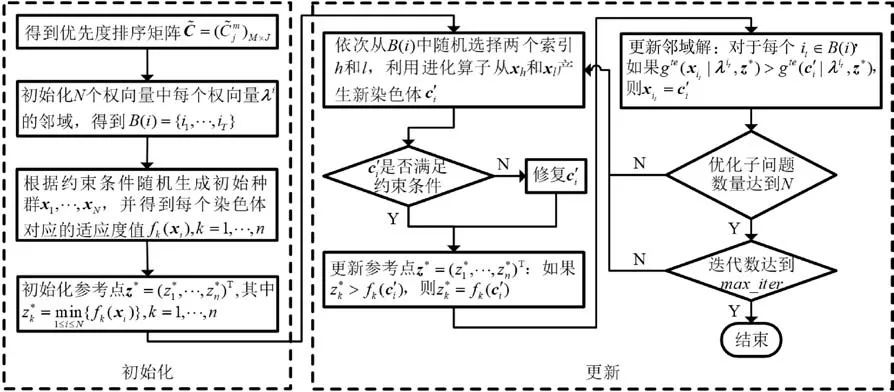
图2 MOEA/D-PS 算法流程Fig. 2 MOEA/D-PS algorithm flow

下面分别对MOEA/D-PS 的优先度排序方法、进化算子、种群的染色体编码方式和初始化方法，以及多目标分解方法进行介绍。

3.1 基于TOPSIS 的需求点优先度排序

面对战场环境下飞机备件往往存在供需不平衡的现象，优先保障重点方向、重点部队的备件需求是战役决策层需要着重考虑的问题。根据作战的特殊性和战场环境的复杂性，本文从作战任务紧迫性1Q、待修部位可更换性Q2、飞机维修时效性Q3和备件需求率Q4共四方面综合考虑，确定不同类型备件下各场站仓库的优先度排序。

式中：t表示作战单位j对飞机故障或战损部位的维修时间；Timemin表示飞机故障或战损部位的最小允许维修时间；Timemax表示飞机故障或战损部位的最大允许维修时间。

需要注意的是，Q2、Q3为效益型指标，指标值越大，作战单位的优先度排序越高；Q1、Q4为成本型指标，指标值越小，作战单位的优先度排序越高，这是因为场站仓库的要求时限越短，作战任务紧迫性越高；备件需求率越小越容易完成对单个作战单位的保障任务，符合战时库存有限情况下的备件供应保障要求。

TOPSIS 方法自1981 年由Hwang 等[17]提出以来，为处理现实世界的多属性决策问题提供了一种有效的途径，在人力资源管理、交通运输、产品设计、工业制造、质量控制等众多领域得到了广泛应用[19]。该方法能充分利用原始数据信息，评价结果能精确反映各评价对象之间的差距，因此本文运用TOPSIS 方法进行不同需求点的优先度排序。

步骤1构造归一化初始矩阵。

步骤2确定理想解和负理想解。

对于第m类备件，其理想解与负理想解分别为

步骤3计算距离。

对于第m类备件，令第j个评价对象与理想解的距离为，与负理想解的距离为，计算公式分别为

式中：wq为第q个指标的权重，且满足。本文采取层次分析法(AHP)[20]计算wq。

步骤4计算相对贴近度。

对于第m类备件，第j个评价对象与理想解的相对贴近度为

步骤5优先度排序。

3.2 种群初始化

以上调度模型涉及的变量是每种备件从各级仓库到需求点的运输量，取值为实数，因此选择实数编码的方式设计种群，种群中每条染色体代表一个可行的调度方案。鉴于本文研究内容考虑多种类型备件，对染色体的编码可分为三部分，具体如图3所示。其中，第一部分根据备件的类型数量，将染色体分为M段，分别表示关于不同备件的调度方案；第二部分针对每一种备件，将染色体第m段分为J个分段，分别表示同一种备件下关于不同需求点的调度方案；第三部分则为同一种备件下关于第j个需求点的具体调度方案，该分段染色体由正向供应、横向转运、紧急配送3 种调度方式构成，其中正向供应又分为后方仓库经野战仓库到达场站仓库，以及野战仓库直接到达场站仓库两种调度 方法。

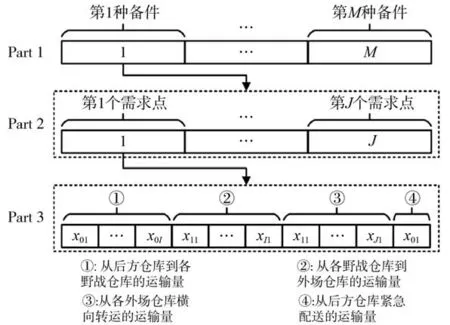
图3 染色体编码示意图Fig. 3 Chromosome coding diagram

在MOEA/D-PS 中，种群由按照图3 编码的一组染色体组成。通过随机初始化保证种群多样性，同时每条染色体必须满足优先度排序、时限要求、库存数量等约束条件，按照优先顺序将每条染色体在约束范围内随机赋值，完成种群初始化。

3.3 进化算子

3.3.1 SBX 算子

SBX 是一种模拟单点二进制交叉的交叉算子，对于多目标进化算法的实数编码，SBX 比其他交叉算子更加适用。假设xh、xl表示从第i个染色体的邻域B(i) = {i1, ···,iT}中随机选取的两个父代染色体向量，ci表示运用SBX 算子产生的子代染色体，公式如下：

式中：θ为由分布因子ηc按照式(40)动态随机 确定：

式中：randij和randc表示在[0, 1]区间产生的随机数；Pc∈[0,1]表示交叉率。当第j个随机数小于Pc时执行交叉操作，否则ci的第j个基因保留父代基因xhj。

3.3.2 多项式变异算子

在经过SBX 操作后产生的ci基础上，按照 式(41)开展多项式变异操作，得到ci′：

式中：

σ1= (cij-lj)/(uj-lj)，σ2= (uj-cij)/(uj-lj)，uj和lj分别表示第j个基因的上、下边界，和randm表示在[0, 1]区间产生的随机数，ηm表示分布因子。当第j个随机数小于Pm时执行变异操作，否则ci′的 第j个基因保留父代基因cij。

3.4 Tchebycheff 分解法

Tchebycheff 分解法是 Zhang 等[16]提出的MOEA/D 中一种经典有效的分解方法，尤其在处理两目标优化问题上具有良好的性能，能够较好地保持种群多样性。通过Tchebycheff 分解法可以将Pareto 前沿的逼近问题转化为具有如下形式的若干标量优化子问题：

式中：z*为参考点，，Ω为决策变量空间，fk(x)为第k个目标函数值，n表示目标函数数量；λ1, ···,λi, ···,λN为一组均匀分布的权向量，其中，N表示子问题数量。通过改变权向量，可以获得不同子问题的Pareto 最优解。

4 案例分析

4.1 案例描述

本文以空军战役军团某次战役实施阶段的备件调度任务想定为案例依据，对所建模型和算法进行验证。根据战役作战方案，执行某阶段作战任务需使用5 种飞机作战平台，共有15 个作战单位参与任务，每个作战单位有对应场站仓库进行备件保障。同时，为形成战时备件供应保障闭环，该作战方向还设置了3 个野战仓库，1 个后方仓库。通过仿真收集战役前期阶段的飞机备件损耗数据，预测得到本阶段飞机备件需求数据，主要包括10 种类型备件(LRU1~LRU10)，具体如表2 所示。三级仓库之间的运输时间如表3 所示，场站仓库关于不同类型备件的要求时限如表4 所示。

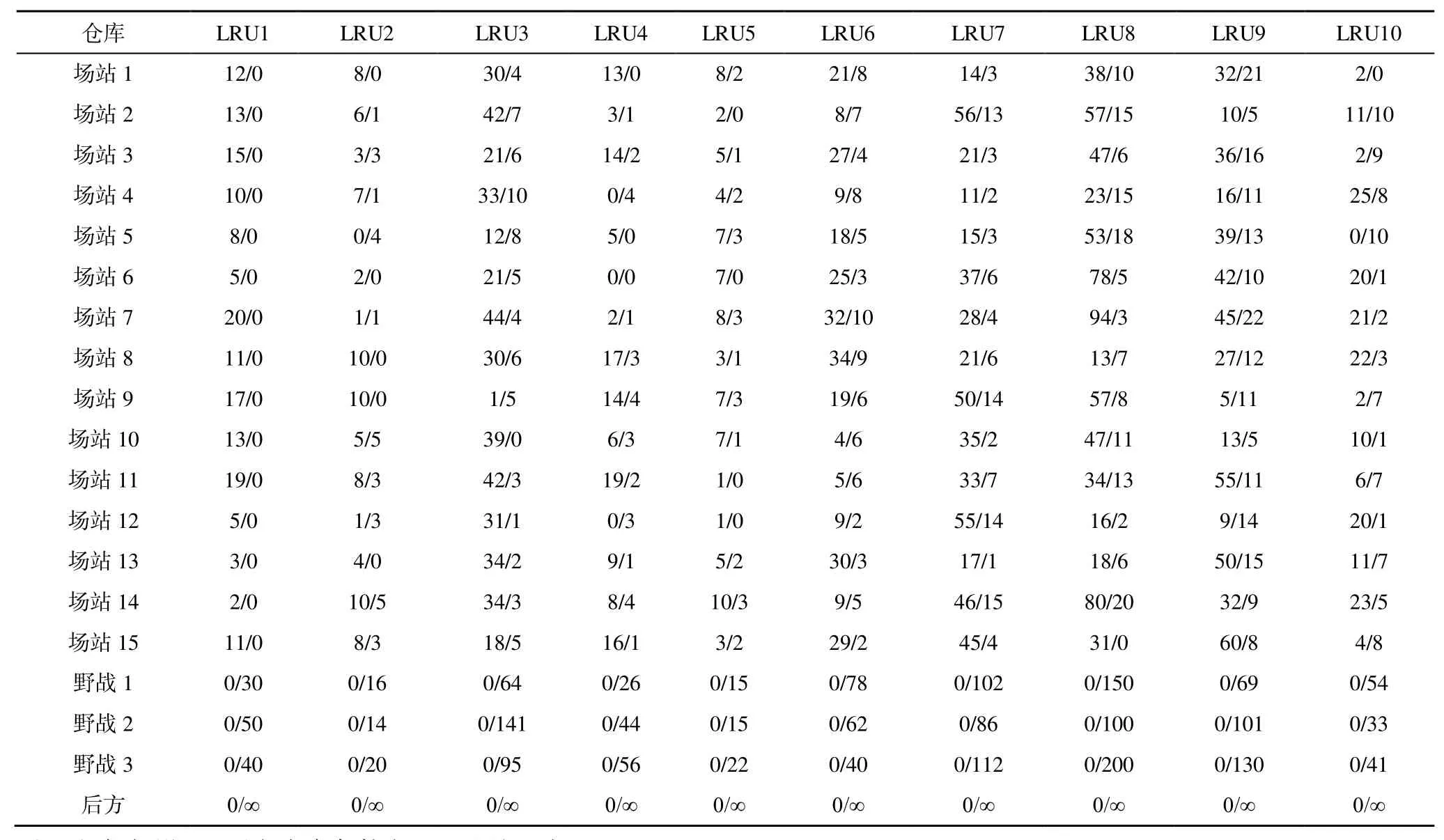
表2 各级仓库关于各型备件的需求量/库存量Table 2 Demand/inventory of various types of spare parts in warehouses at all levels 个

表3 各级仓库之间的运输时间Table 3 Transportation time between warehouses at all levels h

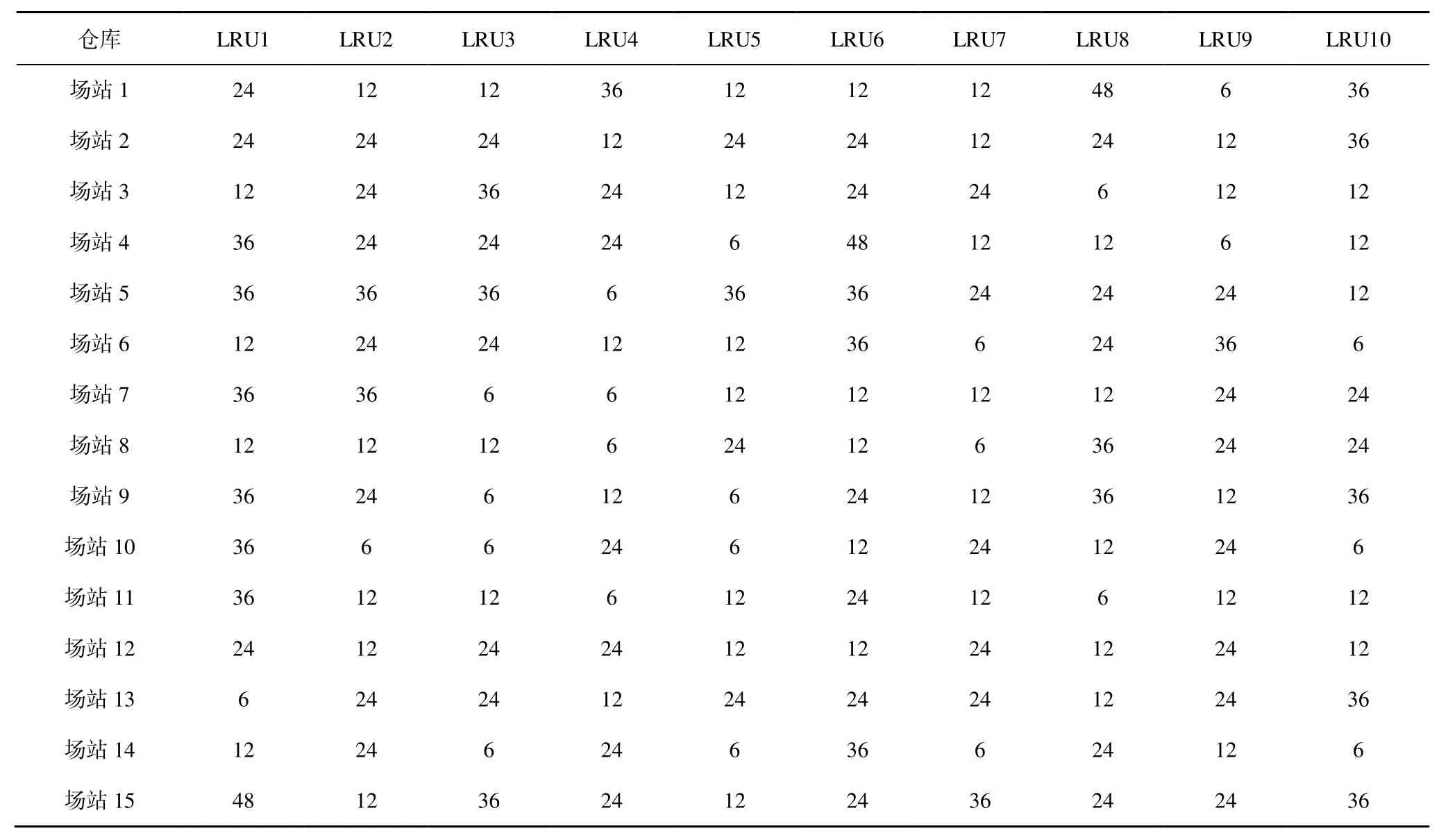
表4 场站仓库关于不同类型备件的要求时限Table 4 Required time limit for different types of spare parts in the station warehouse h

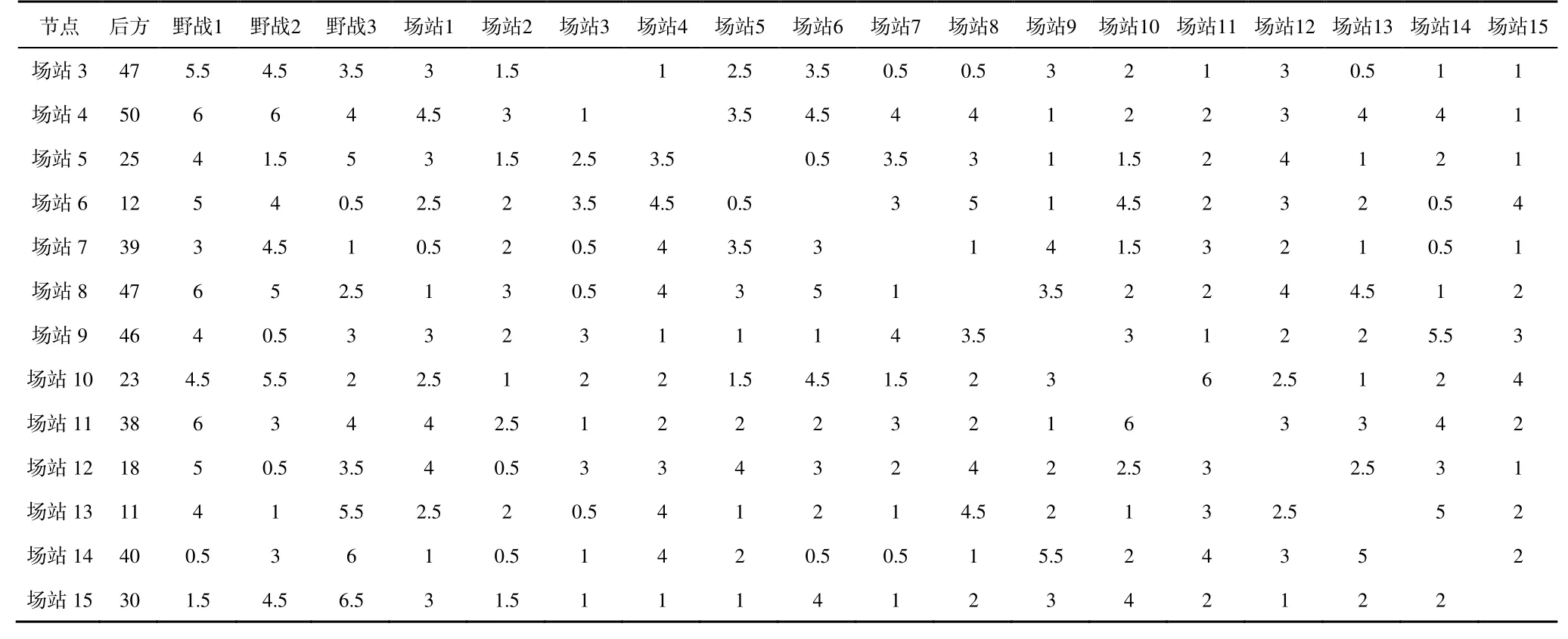
续表3

实验在 Windows10 操作系统上采用MATLAB2021b 进行编程，运行平台为个人笔记本(CPU: AMD R7-5800HS 3.2 GHz; RAM: 16.0 GB)。MOEA/D-PS 算法相关参数设置如表5 所示。

表5 参数设置Table 5 Parameter settings

4.2 实验结果

4.2.1 优先度计算

不同类型备件下各场站仓库关于4 个指标的原始数据矩阵分别为：Q1参照表 4 可直接得到；Q4参照表2 运用式(32)计算可得；Q2和Q3由于数据保密原因，此处直接给出经过式(31)计算和转换得到的结果，具体如表 6 和表 7 所示。

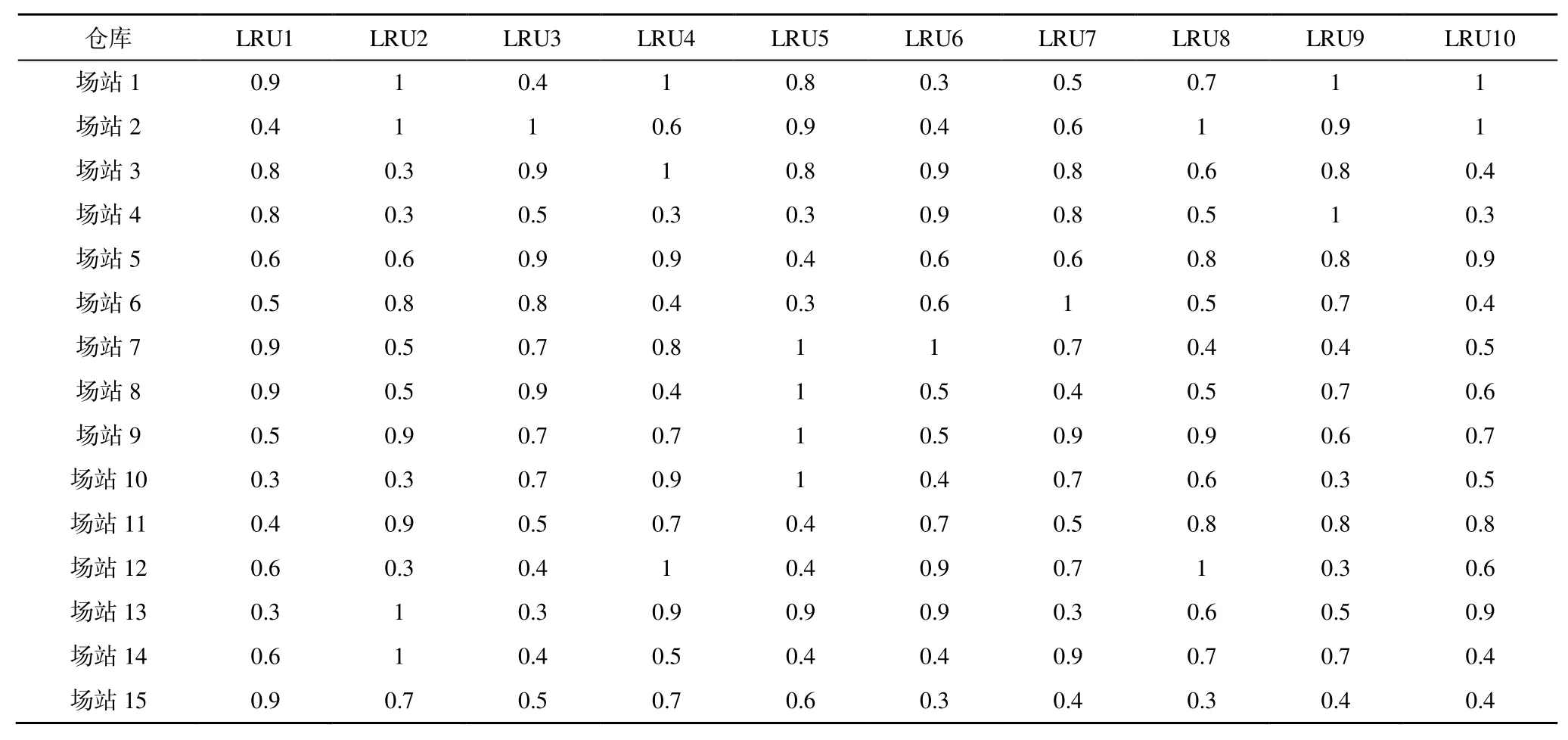
表6 待修部位可更换性Table6 Replaceability of parts to be repaired

表7 飞机维修时效性Table 7 Aircraft maintenance timeliness

根据以上4 个指标的原始数据矩阵，以及由AHP 方法计算得到的指标权重w1~w4均取值为0.25，按照本文给出的基于TOPSIS 的优先度排序计算步骤，得到各场站仓库关于不同类型备件的优先度排序矩阵如表8 所示。

表8 各场站仓库关于不同类型备件的优先度排序结果Table 8 Priority sequencing results of different types of spare parts in each station warehouse

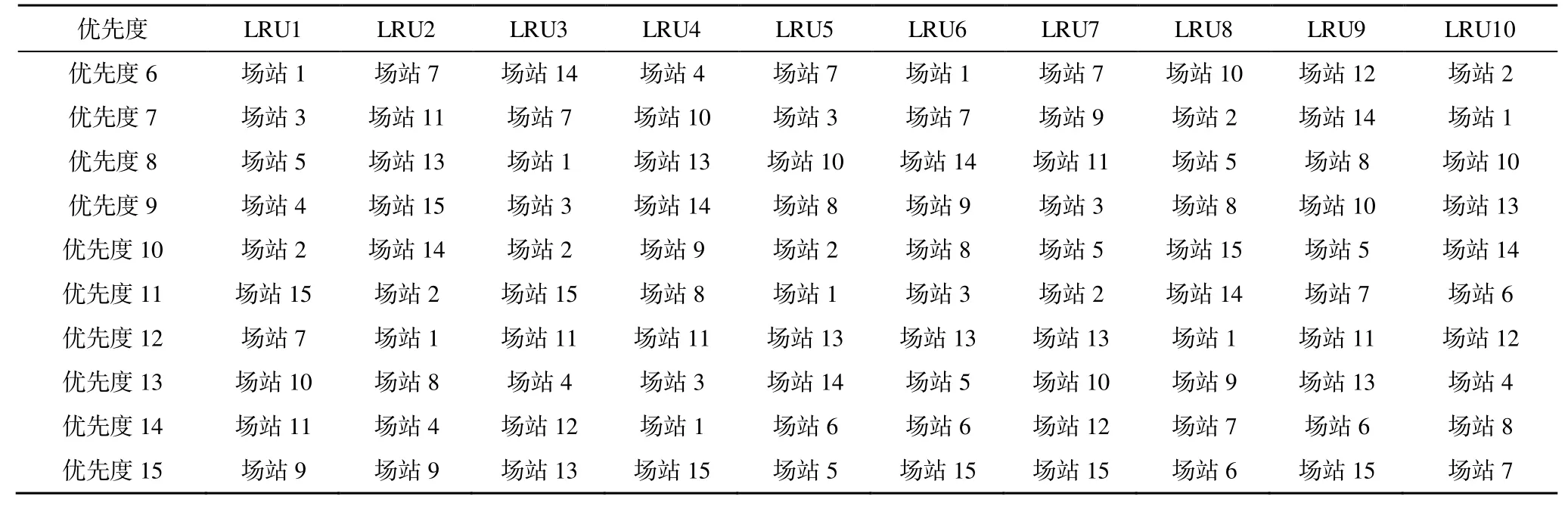
续表8

4.2.2 优化结果

为验证本文构建调度模型及所提算法效果，分别采用MOEA/D-PS 和改进的非支配排序遗传算法(NSGA-II)对4 种备件供应网络的调度模型进行优化。由于本文构建模型以总缺件数最少为第一目标，以总运输时间最短为第二目标，即优先满足备件需求数量，其次优化运输时间。因此从4 种调度模型的Pareto 最优解集中选取总缺件数最少的解进行对比。两种算法各独立运行10 次，选取10 次中目标函数最优结果如图4 所示，具体优化结果及CPU 运行时间均值如表9 所示。

观察图4 和表9 可知，在优先度排序、要求时限、库存数量、算法参数设置等均相同的情况下，两种算法中模型4 的优化结果均为最好，且总缺件数和总运输时间均优于其余3 种调度模型的优化结果，充分证明本文提出的在战时同时考虑正向调度、横向转运和紧急配送的调度策略优于其余3 种调度策略。对于总缺件数而言，模型2 优于模型3优于模型1，表明加入横向转运策略或紧急配送策略均比仅考虑正向调度的策略保障效果更好，同时在现有仓库分布网络中，横向转运策略比紧急配送策略更有助于减少缺件数量和运输时间。

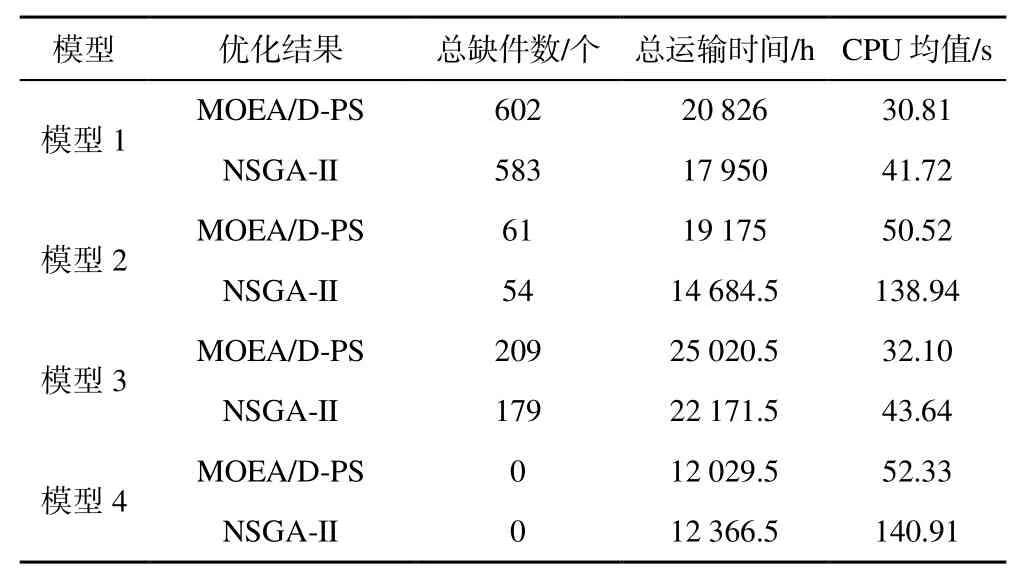
表9 4 种调度模型优化结果对比Table 9 Comparison of optimization results of the four scheduling models

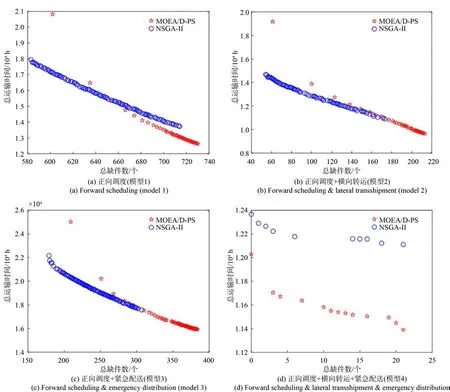
图4 4 种调度模型优化结果Fig. 4 Optimization results of the four scheduling models

另一方面，本文提出的MOEA/D-PS 在4 种模型中CPU 运行时间均值均小于NSGA-II，尤其在决策变量显著增加，调度模型更加复杂的情形下计算速度优势更为突出，以模型4 为例，CPU 运行时间均值缩短62.86%。同时在解的质量方面，MOEA/DPS 在模型4 的最优解支配NSGA-II 的结果。对于其余3 种模型，MOEA/D-PS 与NSGA-II 优化结果相近，略微次于NSGA-II。综上所述，本文算法能够满足战时需要算法兼顾质量和效率的特殊要求。

4.3 优先度排序影响分析

下面进一步分析MOEA/D-PS 相较于MOEA/D的优势。运用MOEA/D 分别对4 种备件供应网络的调度模型进行优化，相关数据和参数设置均与MOEA/D-PS 相同，唯一区别是不考虑优先度排序。算法独立运行 10 次，选取最优结果与MOEA/D-PS 对比，具体如图5 和表10 所示。

图5 两种算法关于4 种调度模型优化结果Fig. 5 Optimization results of the two algorithms on the four scheduling models

观察图5 和表10 可以发现，关于前3 种模型，MOEA/D-PS 在总缺件数方面均优于MOEA/D，而模型4 总缺件数都为0 主要得益于模型4 调度策略的优势，在总运输时间方面MOEA/D-PS依然占优。

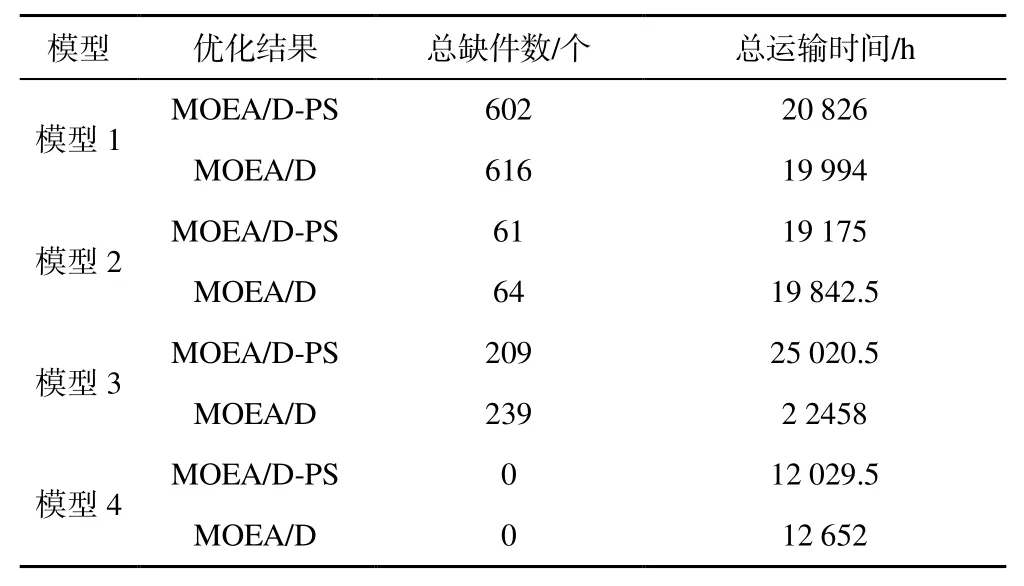
表10 两种算法关于4 种调度模型优化结果对比Table 10 Comparison of optimization results of the two algorithms on the four scheduling models

以上从总体上展示了MOEA/D-PS 的优势，然而其更为重要的优势体现在备件资源的具体分配方案层面。本文以总缺件数最多的模型1 为例进行说明，对比结果如表11 所示。

根据表11 并结合表8 的优先度排序结果可以发现，MOEA/D-PS 能够在战时使得有限的备件资源优先满足需求紧急的作战单位，而MOEA/D 则无法实现这一重要功能，其产生的调度方案容易造成优先度靠前的作战单位不能先于优先度靠后的作战单位得到保障，由此严重影响保障部门发挥职能，甚至影响战役进程和结局。因此，在设计算法时，应充分考虑需求点之间的优先度排序。

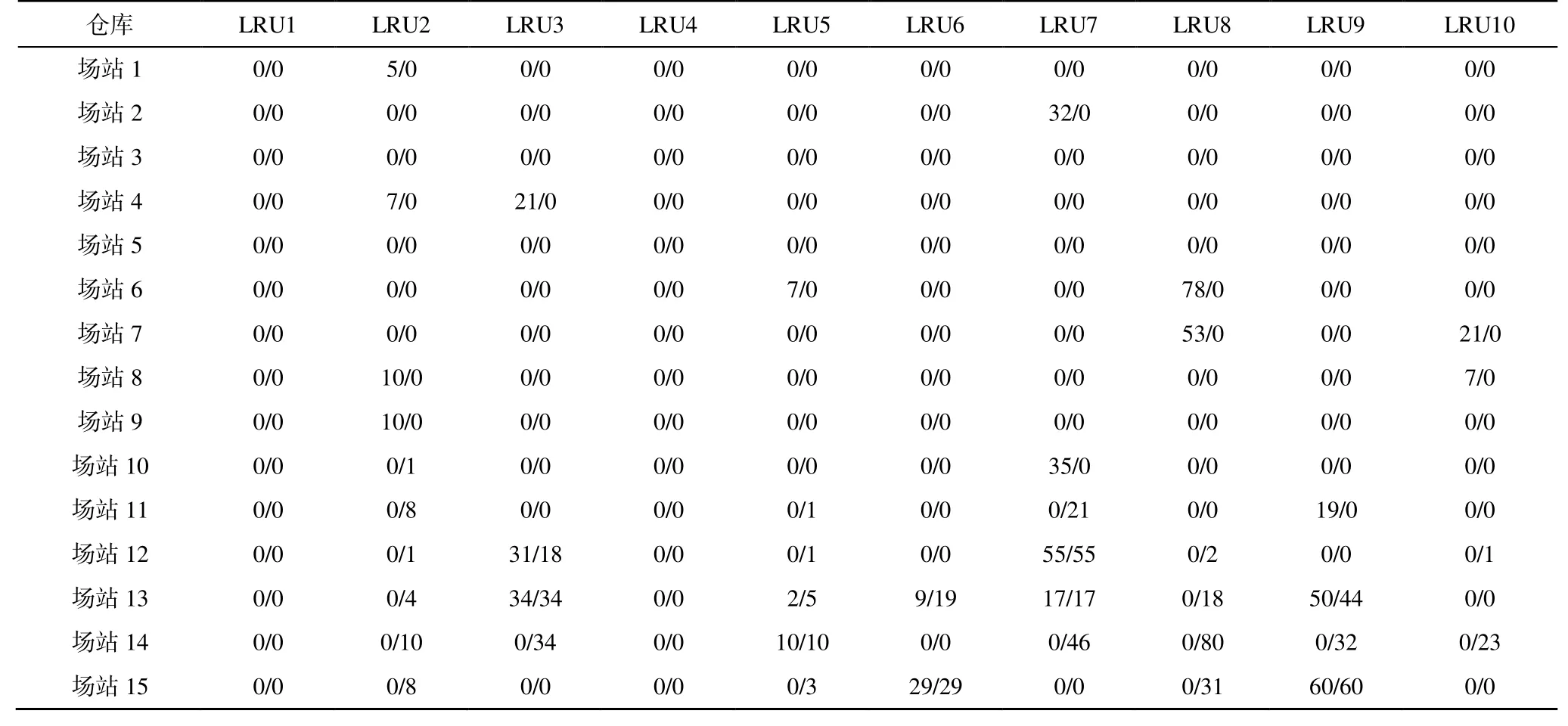
表11 两种算法关于各场站仓库各型备件的缺件数(MOEA/D-PS/ MOEA/D)Table11 The number of missing parts of various types of spare parts in each station warehouse under the two algorithms (MOEA/D-PS/ MOEA/D) 个

4.4 要求时限影响分析

为得到不同要求时限对调度结果的影响，以本文提出调度模型(模型4)为例，依次设置12 h、 24 h、36 h、48 h 为要求时限分析节点，同时增设6 h 和96 h 两种极端情形进行分析，实验结果如 图6 所示。此外，选取各要求时限的Pareto 最优解集中总缺件数最少的解进行对比，结果如表12 所示。

观察图6 和表12 可以发现，两种算法优化结果均表明，要求时限越紧张，造成的总缺件数越多，这是因为严格的时间约束使得大多数备件供应路径不再有效。进一步观察图6 可知，当要求时限为36 h、48 h 和96 h 情形时，多目标优化实则退化为单目标优化。这是因为要求时限足够宽裕时，场站仓库供入量与需求量之间的关系由不等式约束变为等式约束，即场站仓库需求一定能在要求时限内得到满足，由此只需优化总运输时间。

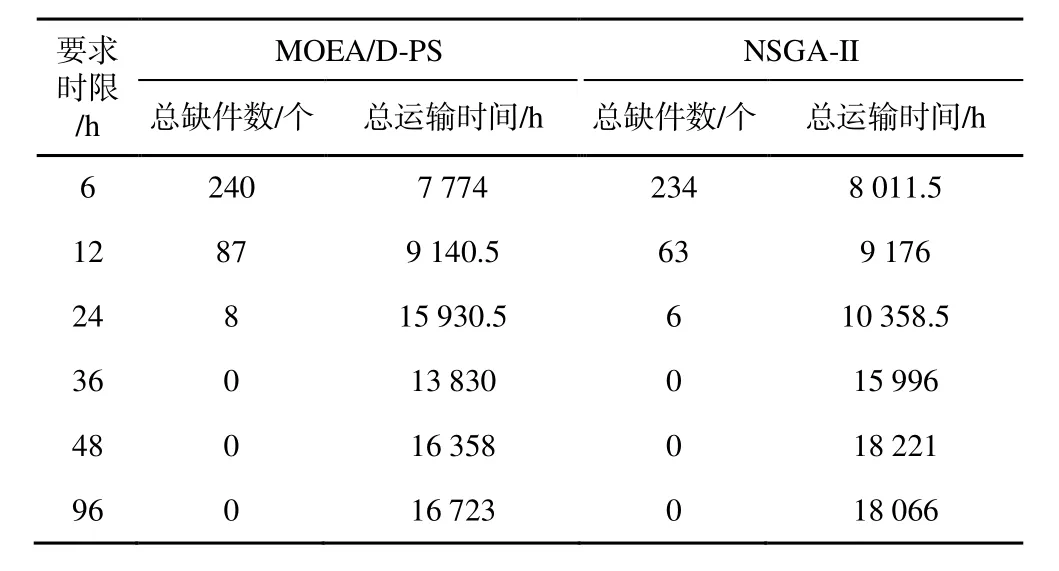
表12 不同要求时限优化结果对比Table 12 Comparison of optimization results under different time limits

图6 不同要求时限优化结果Fig. 6 Optimization results under different time limits

以上分析表明，战场上作战任务的紧迫程度会显著影响备件供应保障效果，符合作战规律。

5 结论

本文针对战时备件调度方案生成问题，以总缺件数最少和总运输时间最短为目标函数构建了能够同时处理多类型备件的新型战时多目标备件调度模型，并设计了MOEA/D-PS 快速求解最优调度方案。得到主要结论如下：

1)新模型在传统正向调度模型的基础上同时加入横向转运和紧急配送策略，克服了现有调度模型灵活性不足以及处理备件类型单一的局限，提高了战役实施阶段对空军战役军团的飞机备件供应保障能力。

2)鉴于战场存在特殊环境需求，备件库存有限且供需不平衡等现象，设计了考虑优先度排序的MOEA/D，即MOEA/D-PS，用于快速生成调度方案，更加符合战时备件调度工作实际。

3)案例分析结果证明了本文所提调度模型相比于其余3 种模型的优越性，充分说明打破飞机备件供应保障制度上的阻碍，有利于增加战时备件供应保障的灵活性，更能激发和挖掘相关保障部门的保障潜力。同时，与经典的NSGA-II 的对比结果表明了本文所提算法能够兼顾求解质量和运算效率。

4)关于优先度排序的影响分析证明了战时备件调度考虑优先度排序的重要性以及本文设计的MOEA/D-PS 相比于MOEA/D 的优势。关于要求时限的影响分析验证了战场上作战任务的紧迫程度会显著影响备件供应保障效果的作战规律。