基于递归图和张量分解的故障可诊断性评价方法

吕佳朋, 史贤俊, 聂新华, 秦玉峰, 龙玉峰

(海军航空大学，山东 烟台 264001)

0 引言

开展装备故障诊断作业对提高装备的使用频率、降低装备维护保养费用具有显著效果。目前对于故障诊断的研究工作主要集中在对故障诊断算法的改进和优化方面[1-2]，人们希望通过改进相关算法获得更高的故障检测率和故障隔离率，同时降低故障虚警及漏检水平。但是，进行故障诊断需要装备提供一定的信息，如果装备是一个不能提供任何故障信息的“黑箱”的话，那么再优秀的算法也无法对装备进行准确的诊断。换言之，只有当故障是能被诊断的，进行故障算法的改进才有意义。当采集到的信息能更真实反映故障的演化情况，能更多地被应用到故障诊断作业的开展中，才能降低故障诊断的难度，从根本上提高装备的可诊断能力[3]。从这个角度看，研究装备故障能否被诊断及诊断故障难度有多大，即对装备进行可诊断性评价，是十分重要的。

目前针对可诊断性评价方面主要有3 种研究 思路：

1)基于定量模型的评价方式。这种方式将目标系统抽象成数学公式，用状态空间、准静态模型、差分方程、传递函数等表示实际的物理系 统[4-7]，而后利用奇偶关系、能观能控等矩阵论或控制论的相关理论，对目标系统的可诊断性进行评价分析[8-10]。

2)基于定性模型的评价方式。这种方式普遍采用的方法是D 矩阵，D 矩阵是一种表征故障与测试之间关系的二值矩阵，通过D 矩阵可以清楚发现“哪些故障可以被诊断”等问题。该方法的总体思路是首先通过D 矩阵对故障的可检测、不可检测、可隔离、不可隔离的性质进行定性研究，而后通过定量计算的方法，对故障的可诊断性和整个系统的可诊断性进行量化计算。更进一步，在该评价方式的具体实现细节上，目前文献主要有两个不同方面：1)D 矩阵中元素表达多样化，即将原来的二值化D 矩阵变为多值化矩阵，使得矩阵的内涵更丰富，Liu[11]使用整数代替原来D 矩阵中仅有0 元素和1 元素的情况，其中元素的符号表征故障对测试信号的增强或削弱作用，而元素的绝对值表示测试的时滞性。2)D 矩阵获取方式多样化，传统的D矩阵是通过信号流图或多信号模型获得的，现在可以通过结构模型、SDG[11]、键合图[12]等方法 获得。

3)基于数据的评价方法。主要是利用历史数据的统计规律进行可诊断性问题的评价[13-14]。例如采用主成分分析(PCA)方法将历史数据分解成为主子空间和残差子空间，在残差子空间利用SPE 和T2两种统计量来对故障可诊断性进行理论分析[15-16]。

但是在实际过程中，思路1 虽然具有很高的理论性，但是该思路所推导的前提是建立在正确获得目标对象的数学表达式的基础上，在现实情况中，数学表达式的建立是很困难的，并且还有未建模动态等因素的影响，这使得目前该方法的实际应用范围大大受限，目前实际应用局限于动量轮[17]等装备中的一些重要元器件，尚未看到有对整个系统级装备进行研究的用例。思路2 中采用D 矩阵的方法来对可诊断性进行评价，D 矩阵的构建实质上仅仅考虑了装备的结构因素，但如文献[3]中所述，影响可诊断性的因素是多种多样的，表明仅仅考虑其中的系统构型和配置因素显然是不完备的，不足以支撑开展故障可诊断性评价工作。思路3 使用统计的方法，对于数据量的要求是十分巨大的，同时目前的文献只局限于理论分析方面，尚未见到实际应用。

思路3 使用的是装备的历史数据来反映装备的信息。这些信息给了我们启发：在日常生活中，人们最常用的是通过传感器来感知装备的状态。装备的模型结构固然会对评价装备可诊断性产生影响，但是传感器的信号会为评价可诊断性带来更多的信息，从信号中可以提取不同状态下系统的典型特征，以典型特征的差异程度作为系统不同故障状态的差异程度，可以使得装备可诊断性的评价更加客观。

基于上述想法，本文将信号引入到对系统可诊断性的评价，利用信号的特征作为各故障状态的基本特征。而在特征的提取上，本文采用相空间重构和递归图的方法，这是一种将一维信号二维化(图形化)[18]的方法，可以借助模式识别的相关理论，对原信号中的混沌性等特征进行提取。最后通过张量分解的方法对特征的相异程度进行度量，作为可检测性和可隔离性评估的依据。

1 考虑信号的可诊断性数学化表达

文献[3, 19]指出，可诊断性是系统故障能够被准确地、有效地识别的程度。在目前的研究中，故障可诊断性包括可检测性(detectability)和可隔离性(或可分离性)(isolability)[8,19-22]。

从上述定义中可以看出：1)可诊断性是装备系统诊断能力的一个度量，它不同于故障诊断，故障诊断是对故障进行检测、隔离的过程，而可诊断性是装备系统的一个属性，该属性揭示了故障被检测和隔离的难易程度；2)可诊断性作为装备诊断能力的衡量，实质上衡量的是不同状态之间的差异程度。

这里的差异程度在可检测性的概念中是指故障发生后，系统能够表现出与正常状态有所差异的能力。在不考虑诊断手段以及诊断算法的条件下，故障状态下信号所反映的特征和正常状态下信号所反映出的特征差别越大，则说明故障被检测的可能性越大，越容易被检测出来，可检测性越高。

同理，在可分离性的概念中，差异程度是指对于不同故障，系统所具有的不同表现形式的能力。在两种不同的故障模式下，信号的特征差别越大，则两种故障模式的区分性就越大，故障被混淆的可能性就越小。而针对某一种故障模式，同其他所有的故障模式差距都很大时，该故障在诊断时就可以很容易地和其他故障模式区别开来，即该故障的故障可隔离性很大。

可以定义故障的可检测性：

式中：FDi表示故障模式fi的故障可检测性；function1 为映射：

故障的可隔离性为

式中：FIij表示故障模式fi和故障模式fj的差异程度；FIi表示故障fi的可隔离性。

2 基于递归图的故障信号图形化表征及信号特征提取

一般的装备信号经过一定的时间演化会表现出一种周期递归状态。这种递归状态揭示了系统(信号)回到特定动力学状态的行为运动。Packed 等首次提出了利用重构非线性时间序列相空间重构的方法来研究这种周期递归的非线性动力学特征。Takens 从数学上证明了重构的相空间可以保留原系统的动力学特性，为基于相空间重构的递归图的大规模应用提供了理论依据。

基于相空间重构的递归图，通过二维平面内的黑白点对相空间中的状态进行可视化，能够揭示信号的递归规律，是一种很好的动力学主流形描述方法。本文将递归图所表现出来的递归性作为不同信号所表现出来的基本特征。

根据嵌入维度和延迟时间，对时间长度为N的离散时间序列进行相空间重构，形成如下式所示的行dim列的重构像空间。

计算递归图中递归值：

式中：ε为阈值，阈值的大小只能影响到递归图中点的疏密程度，并不能改变图的结构，在本文中，阈值选取为相空间中任意两向量中距离最大值的10%；为Heaviside 函数。

通过式(7)，可以获得一个 阶的0-1 二值方阵R，按照“0 用白点表示，1 用黑点表示”的规则，将矩阵R绘制在坐标轴上即可得到递归图。

递归图点的疏密程度以及线结构能够反映出原始信号的特征，在递归图的基础上，Marwan 提出了递归定量分析(RQA)的方法，该方法确定了递归图中的递归率、确定性、层流性以及递归熵来描述原始信号的动态特性。由于该方法具备所需数据量少，抗噪声能力强的特点，而成为一种非线性特征提取的方法，被应用到各种领域。

重构像空间4 种特征参数计算方法及物理含义如表1 所示。

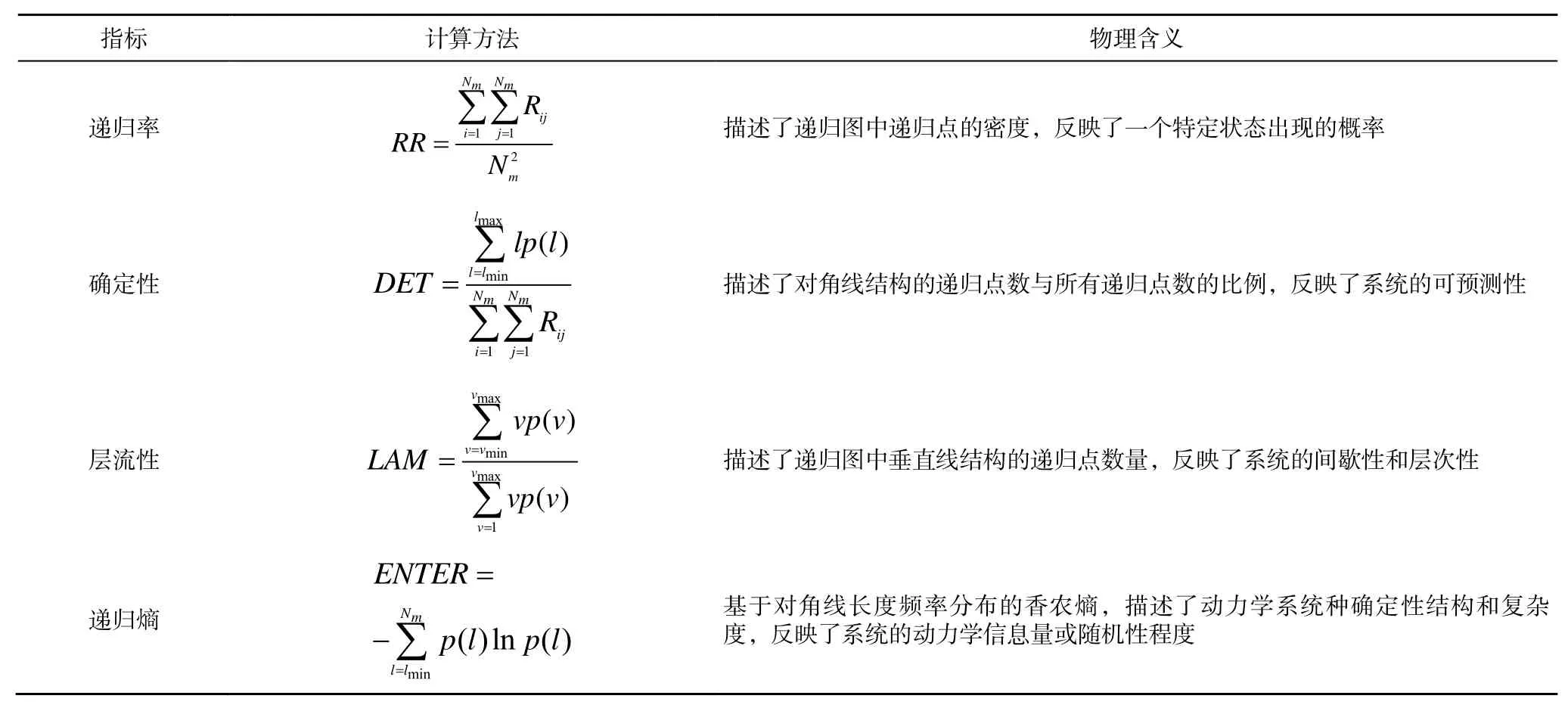
表1 递归图特征指标及物理含义Table 1 Characteristic index of the recursive graph and their definitions in physics

表1 中，lmin和lmax为对角线方向直线的最大、最小长度；vmin和vmax为垂直方向直线的最大、最小长度；p(l)和p(v)分别表示递归图中对角线和垂直方向直线的长度分布，分别定义为

式中：Nl为对角线方向长度为l的直线的条数；Nv为垂直方向长度为v的直线的条数；为长度为的对角线方向以及垂直方向的直线的条数。

3 基于张量分解的可诊断性表示

在第1 节中针对装备m种故障模式假设的基础上，进一步假设装备共有n个测试点，其集合表示为。注意到测试点是为了方便装备测量信号而预留的电气上的物理连接口，但这种物理接口和信号并不是一一对应的关系，即从一个物理测试点中可能测量多路信号。假设从测试点中共能测得种不同的信号，则测试点集合可以进一步表示为，这里表示第i个物理测试点的第j种信号和信号是一一对应的关系，部分文献称其为虚拟测试点。为叙述方便，在后续行文中若未加说明，则测试点是指虚拟测试点。

图1 矩阵SD示意图Fig. 1 SDmatrix

从图1 中可以看出，该矩阵的行代表了装备不同故障模式下通过测点测到的所有信号。

对于矩阵SD中任意一个信号，均可以通过第2节所示的方法，通过递归图和递归定量分析计算出该信号的特征。所有向量的特征可以构成一个特征张量，将特征张量按照模态1展开，得到

式中：m+1 表示装备故障模式数目(包含装备正常状态)；表示所有测试点的数量(即信号的种类数)；k表示通过递归图所提取的特征的数量。需要说明的是，式(10)中张量的展开从0 开始计算，是为了与前述 表征正常状态的下标相对应。张量的含义及其展开示意图如图2 所示。

根据第1 节的描述，可诊断性实质上是对不同状态下信号特征差异性大小的度量，则通过 图2 所示的张量分解过程，可诊断性的评价问题转变为特征张量中任意两个2 阶张量的差异性度量的问题。

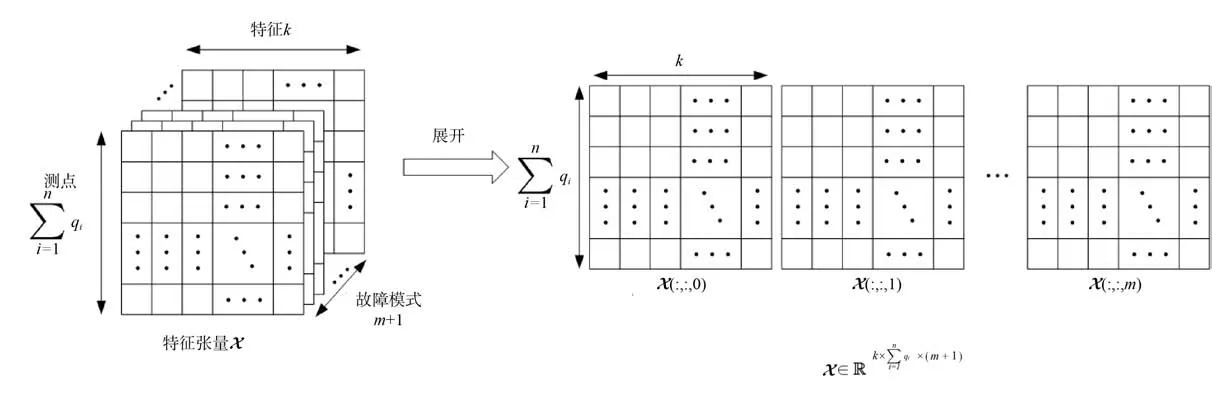
图2 特征张量X 及展开示意图Fig. 2 Feature tensorX and its expansion

Ahmad Borzou 等[24]提出一种相关性系数的方法来度量两个2 阶张量的差异性，该方法对数据的大小具有较高的鲁棒性，同时能够消除低样本数据中的相关性高估问题，因此得到广泛 应用。

定义张量D为式(10)中任意两个2 阶张量的内积，即

对张量D进行分解：

式中：tr(·)表示迹运算；J表示D的维数；E表示J阶单位矩阵。

将式(12)进行拆分：

式中：A1、A2、B1、B2为将A和B按照式(12)和式(13)进行分解得到的分量，A=X(:,:,i) ,X(:,:,i)，B=X(:,:,j) ,X(:,:,j)。

将式(14)中的3 个指标取几何平均值，作为相似衡量的最终结果。

式(15)描述的实际上是 2 阶张量X(:,:,i)和X(:,:,j)之间的相似性，即故障模式fi和故障模式fj之间的相似性，而根据第1 节的论述，可诊断性实质上是对差异性的描述，状态间的差异性越大，则可诊断性越大。由此对式(15)进行变形，得：

式(16)是对2 阶张量 X (:,:,i)和 X (:,:,j)差异性的度量，即状态fi或fj的差异性。当fi或fj中任意一个状态对应正常状态时，则式(16)表达的是故障可检测性，即式(1)的内涵，当fi或fj中对应的是任意两种故障模式时，则式(16)表达的是式(2)的内涵，进一步，可通过式(4)求得故障模式i的可隔离性。

4 算法流程设计及实现

按照第2 节和第3 节的原理，本文所提出的一种基于递归图和张量分解的故障可诊断性评价算法流程如下：

步骤1信号提取。对装备各状态下各测点信号进行提取，按照图1 所示构成矩阵SD。

步骤2故障信号的图形化表示。对SD矩阵中的任意一路信号，构建递归图；

步骤2.1：信号离散化，同时确定各信号的参数嵌入维度dim和延迟时间 ；

步骤2.2：根据嵌入维度和延迟时间，通过 式(5)对原信号进行相空间重构；

步骤2.3：在重构的相空间中，按照式(6)和式(7)确定递归值，并根据阈值的大小绘制递 归图。

步骤3特征提取。针对任意一张递归图，按照表1 所述，进行特征值的计算和提取。

步骤4可诊断性评价。

步骤4.1：将所有的信号进行特征提取，则可以构成特征张量X；

步骤4.2：将特征张量X按照模态1 展开，即可得装备不同状态下所对应的张量；

步骤4.3：对于任意由特征张量X展开的两个张量，按照按照式(11)~式(15)进行张量相似性度量；

步骤4.4：根据步骤4.3 的结果，按照式(16)对装备的可诊断性进行估计。

该算法的示意图如图3 所示。

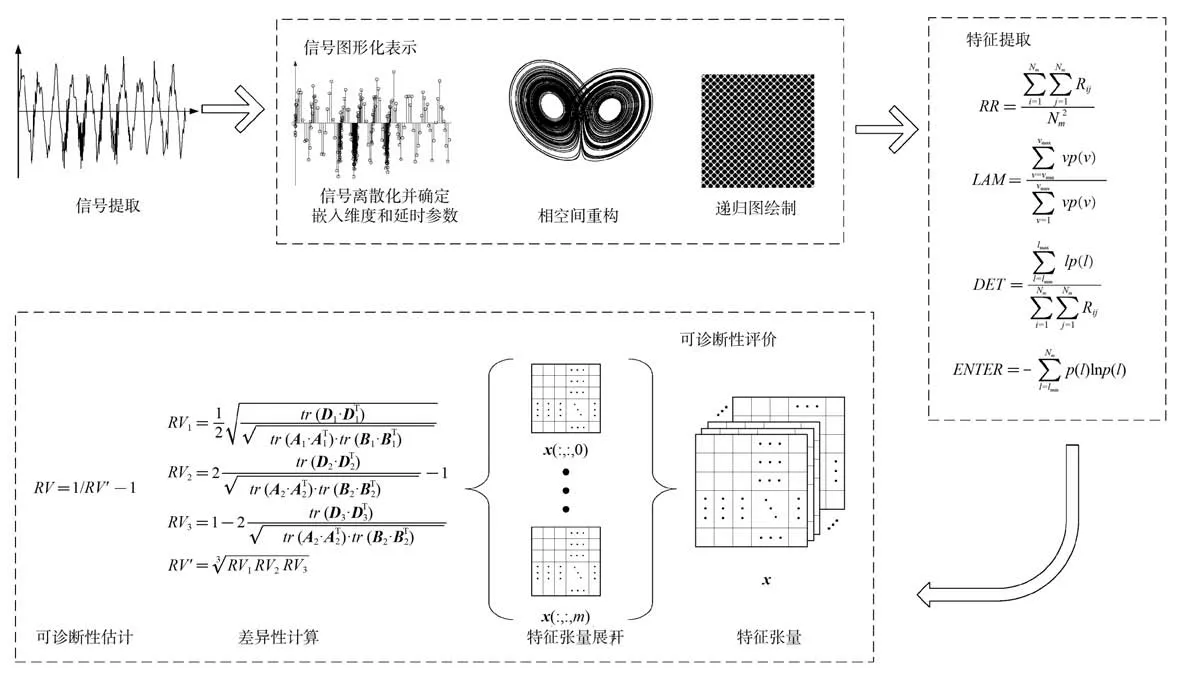
图3 算法流程示意图Fig. 3 Flowchart of the algorithm

5 仿真实验

本文选取一模拟电路来进行仿真，该电路包含运放子电路、滤波子电路、三极管子电路，能充分展现模拟电路中一般故障情况，故用此电路说明本文故障可诊断性评价方法的有效性和优越性。

5.1 实验说明

该模拟电路的电路图如图4 所示，其中电路电源为正弦交流电源。电路共设置4 个测试点，每个测试点输出一路电压信号。实验电路模拟的故障如表2 所示。

图4 电路图Fig. 4 Circuit diagram

表2 典型故障模式Table 2 Typical fault modes

使用Multisim 软件按照表2 所示的模式对电路故障进行仿真，仿真电路图如图5 所示，并收集相关信号，对电路系统的可诊断性进行评价。

图5 电路仿真图Fig. 5 Simulated circuit diagram

本文选用两种方法对电路系统的可诊断性进行评价，一种是本文方法(以下简称A 方法)，另一种是目前生产实践中最常用的D 矩阵方法(以下简称B 方法，其具体步骤可参见文献[17, 25])进行对比说明。

5.2 实验结果

1) A 方法

通过A 方法计算得到的各个状态之间的可差异性如表3 所示。

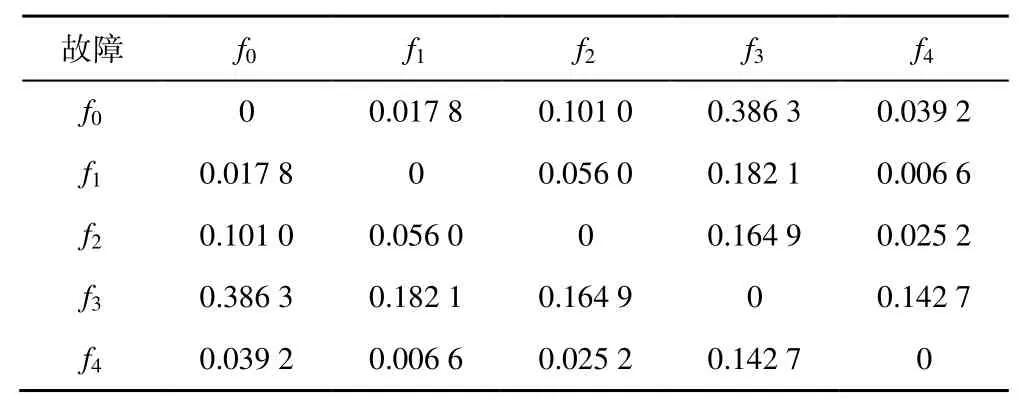
表3 各状态之间差异性Table 3 Difference between states

进一步可以得出各个故障的可检测性和可隔离性分别如表4、表5 所示。

表4 故障可检测性Table 4 Fault detectability

表5 故障可隔离性Table 5 Fault isolability

通过表3，可以首先得出定性的结论：所有的故障都可以被检测和诊断。但是不同故障检测的难易程度有所差异。通过表4 可知，在表2 所示的所有故障模式中，故障可隔离性能从易到难为：f3＞f2＞f1＞f4。

2)B 方法

根据如图3 所示的电路图，可以得出相关D矩阵，如表6 所示。

表6 电路图D 矩阵Table 6 D matrix of the circuit diagram

通过表6 可以得到：

1)可检测故障：f3,f2,f1,f4；

2)不可检测故障：∅；

3)可分离故障：∅；

4)不可分离故障：{f1,f2} , {f3,f4} 。

根据上述分析可以得出故障及系统的可诊断性度量指标分别如表7、表8 所示。

表7 各故障的可诊断性度量指标Table 7 Diagnosability index of faults

表8 系统可诊断性度量指标Table 8 Diagnosability index of the system

5.3 实验结果分析

从表3~表7 的结果中看出，两种方法均认为 4 种故障模式可以被检测，不需要后期再添加相应的测试接口。但不同的是：B 方法认为存在故障对{f1,f2}和{f3,f4}是不能分离的，即原系统若需要进一步对两对故障对进行诊断，则需要增加额外的测试；而A 方法认为现有的测点足够将故障分离开来，同时还给出了4 种故障隔离的难易程度。

5.3.1 关于不可分离故障对的分析讨论

故障对{f3,f4}是关于电容C1的故障模式，在本电路中，电容C1和电阻R4构成一个滤波电路，可以对相关噪声进行滤除，当 被击穿时，实质上是处于短路状态，此时测点3 和测点4 不会检测到信号，而当C1发生泄露，滤波电路的功能会受到影响，但此时依然会有信号通过。表明在两种故障模式下，通过测点3 和测点4 信号可以对故障{f3,f4}进行区分。两种故障模式下测点3 的信号如图6 所示。

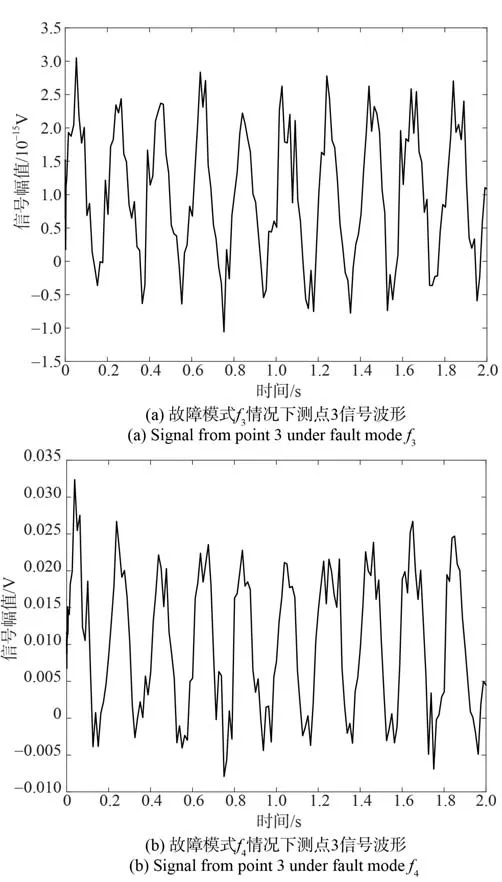
图6 故障模式f3、f4情况下测点3 信号波形Fig. 6 Test point 3 signal under fault modef3andf4

从图4 中可以看出，当电容C1发生短路故障时，测点3 几乎检测不到信号，仅能测试到噪声，而当电容发生漏电事故时，测点3 仍能检测到信号波形。

故障对{f1,f2}是关于运放电路的故障模式，在本电路中，电阻R1和R3以及运算放大器OP1构成同向运算放大电路，电阻R1和R3的开路故障，导致的测点2 的信号如图7 所示。

从图7 中可以看出，故障模式f2使得运放OP1无法正常工作，导致输出波形已经完全失真，从信号的角度看，故障f1和f2是完全可分的。

由此可见，如果只考虑装备的结构，即仅仅从故障是否对测点信号产生影响的角度看，则有的故障是无法被隔离的；如果考虑信号，则实质上不光考虑了故障是否对测点产生了影响，还考虑了产生的什么样的影响，使得用于故障诊断的信息大大丰富，更有利于说明故障的可诊断性。

5.3.2 关于故障可隔离度的分析

A 方法给出了4 种故障模式的可隔离性大小，通过前述分析可知，故障2 和故障3 分别导致运放OP1和滤波电路完全丧失作用，使得测点2 和测点3的信号发生严重畸变，因此该两种故障是最为容易隔离的故障，而故障1 和故障4 仅仅使得放大器和滤波电路的性能发生变化，故障具有一定的可隔离性。说明A 方法得到的最终故障隔离的难易程度的排序具有一定的可观性。

6 结论

为了评估装备的可诊断性，本文提出了一种基于递归图和张量分解的评价方法。之前传统的可诊断性评价方法仅仅围绕装备的结构信息展开，本文在此基础上，同时考虑了测试点的信号信息，来对故障能否被检测以及故障检测的难易程度等问题进行了更科学具体的评价。实验结果表明，本文的方法能正确反映故障的可检测性，同时对于故障隔离性能够进行客观的量化评价。这种量化的评价结果，为后续工作中使用优化方式进行测试点的选择和优化配置打下了基础。