培养中学生数学思维策略的研讨与实践

张凤洁

思维本来就是人们讨论的热门话题，2022年新课标的出台，又增强了教师们对思维的认识和重视。思维在各个学科中都有所体现，但不可否认，在数学学科中体现得更为明显。在中学数学教学中，我们要有意识地把思维融入数学的各个知识点、能力点的教学中，切实地提高中学生的数学思维能力。

一、数学思维的基本形式：分析与综合

科学家通过研究发现，思维是人脑的一种机能，是人脑对客观事物的一种反映。巴甫洛夫根据大量的实验材料证明，思维其实就是人们对事物分析与综合的过程。如人们对于自然和社会的认识，都是在分析之后又立即加以综合的结果。在森林里，可以把树木分析为根、干、枝、叶，乃至木柴的组成部分，然后又把根、干、枝、叶等结合为“树木”，又把许多树木结合为“森林”。人们对事物的认识，必须经过分析、综合，综合、分析，才能使认识更加全面和深刻。

在数学学习中，经常要用到比较的方法。其实，比较既是分析的过程，也是综合的过程。常言“有比较才有鉴别”“在比较中认识一切”讲的也就是这个意思。可以说，比较是数学教学和研究中非常重要的一种方法，在中学数学教学中加强比较教学，有利于学生掌握知识，提高数学能力。此外，比较可以简化相似问题的研究，在不相同的对象中探求相同点，或在相同的对象中探求相异点，这样才有利于对问题的研究。无论是在数学学科还是其他学科教学中，比较的类型都有相同点比较和异同点比较。在数学教学和研究中，运用比较应注意比较必须在同一关系下，按照一定的步骤进行；对于数学对象的同一性质所作的比较，应当是完整、彻底的，而不应该是片面的、肤浅的。

分析与综合是基本的思维方法，是思维活动的基本过程。分析与综合在任何一种智力活动中都是彼此密切联系的。分析是在综合指导下进行的，综合是在分析的基础上进行的。当代自然科学发展的根本特点，一方面是高度分化，一方面又是高度综合，或是多种学科的综合、学科内部的综合。对于数学学科来说，同样存在高度分化、高度综合的现象。人们对数学的认识是不可穷尽的，因此，在数学中这种分析、综合的过程也是无止境的。

二、数学思维结构主义学派

由于数学方法的层次并没有一个较为明确的分类标准，所以，我们将以数学的一般方法与数学的特殊方法来研究和探讨。数学中许多的数学思想、方法和技巧，都将隶属于这些研究方法之中。

本世纪30年代左右，法国一批优秀的青年数学家，不满于老一代的守归传统，怀着闯新路的热情，共同合作研究，成立讨论班，逐步形成一个数学学派，布尔巴基是这批年轻数学家所用的一个共同笔名，因而结构主义学派又称为布尔巴基学派。这个学派的结构化思想，不但在数学界，而且在哲学界、心理学界都引起了强烈反响，对中学数学改革也产生了很大的影响。

只是到了本世纪30年代前后，法国的布尔巴基派从全部数学中提炼出三种母结构，数学的各分支可以按照这三种结构的不同组合加以区别和归类，这种分类当然比传统的分类方法深刻得多。

结构主义观点反映在数学教学领域，曾导致“新数”运动。“新数”运动给数学添加了一些有活力的思想，增加了一些科学成果，尤其是在强调数学的直观性、实验性、趣味性等方面，具有积极的作用，纠正了不少学生害怕数学的观念。不足的是，结构主义学派的方法论，专注于数学形式结构特征的分析与比较，其主要兴趣是一种对已经形成了的数学部门的回顾性的逻辑分析和整理工作，而不是注意研究如何从现实世界中提取新的数学模型，开辟新的数学领域，无法激发学生的直觉想象能力，因此，结构主义的基本思想方法不是一种发明创造的方法。

结构主义方法既有它的积极作用，但也有一定的局限性。按照传统的分类方法，人们总是习惯于把数学分为代数、几何、分析三大类。按照这种分类，一些不同的数学对象，却说不清楚它们之间的区别究竟是什么，而另一些不同的数学对象之间却有着明显的共同点。例如，数的加法、多项式的加法、向量的加法等等，它们为什么都叫“加法”？实数和复数都可以进行四则运算，都有绝对值，似乎差别不大，但是复数偏偏没有大小，为什么复数无大小？实数与复数的本质区别是什么？这些问题按传统的分类方法都无法说清楚。

三、数学思维：发展学生空间想象力

在中学数学中，不仅要研究数与数、形与形之间的关系，还要研究数与形之间的关系。研究形与形之间的关系，要应用图形来解决一些问题。同时，随着人们对于一维空间（例如直线）、二维空间（例如平面）、三维空间（例如正方体）中的空间形式的深入研究，不断发展对于“空间”概念的认识。“四维空间”的思维空间，各种抽象空间都被现代数学所研究着，并获得了广泛而深刻的应用。因此，我们在中学数学教学过程中，不仅要使学生形成积累空间观念，要让学生掌握空间形式的常用表达方法，还要研究图形之间的关系，发展学生的空间想象力。图形之间的关系可以分为三类：一是同类图形之间的关系，二是不同类图形之间的关系，三是数与形之间的关系。

1. 同类图形之间的联系

三角形的全等与相似是平面几何的基础内容之一，应当结合它们的教学不断丰富空间想象力，提高逻辑思维与运算能力。

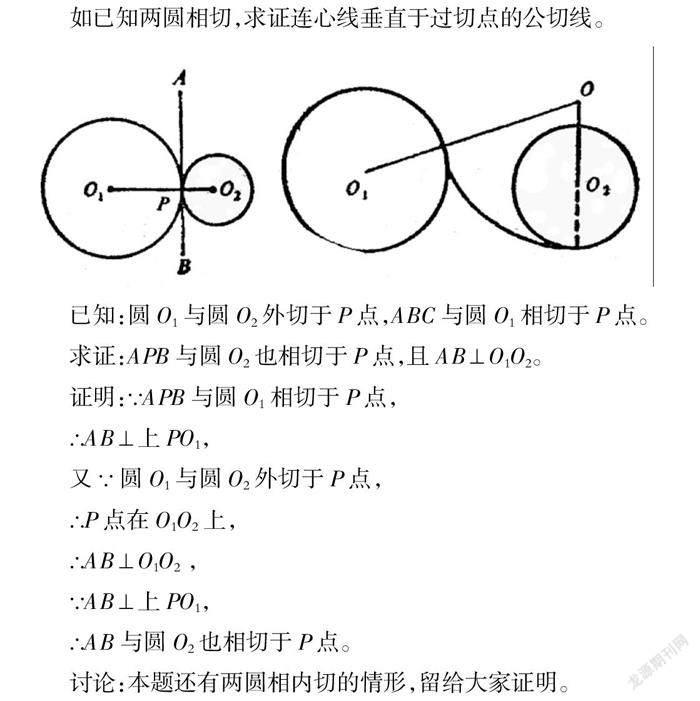
圆与圆的位置关系比较复杂，但可以归纳为如下最基本的五类：相离、外切、相交、内切、内含。主要定理有：两圆相交，连心线垂直平分它们的公共弦；两圆外切，切点在连心线上，圆心距d=R+r，反之也对；两圆内切，切点在连心线上，圆心距d=R-r，反之也对；两圆的两条外公切线相等，两条内公切线也相等。

如已知两圆相切，求证连心线垂直于过切点的公切线。

已知：圆O1与圆O2外切于P点，ABC与圆O1相切于P点。

求证：APB与圆O2也相切于P点，且AB⊥O1O2。

證明：∵APB与圆O1相切于P点，

∴AB⊥上PO1，

又∵圆O1与圆O2外切于P点，

∴P点在O1O2上，

∴AB⊥O1O2 ，

∵AB⊥上PO1，

∴AB与圆O2也相切于P点。

讨论：本题还有两圆相内切的情形，留给大家证明。

因为两圆相切时，圆弧和圆弧在切点处平滑地连接起来，所以在实际中有许多应用。

一般称两圆外切的连线为外连接；两圆内切的连接为内连接。画连接图时，主要矛盾是如何确定圆心的位置。

2. 不同类图形之间的联系

不同类图形之间的关系比较多，也相当复杂。其中，圆和多边形的联系是平面几何中最主要的关系，大量的习题都与此有关，我们在教学时要注意对这类问题的分析。另外，还有圆与三角形、圆和四边形、圆和正多边形等各种关系。

3. 数与形之间的联系

在中学阶段，数与形的关系主要体现为锐角三角函数与勾股定理的关系、坐标法。我们在教学中，应当教会学生有关的基础知识，同时，要有意识地发展他们的空间想象力，并进行唯物辩证法的教育。

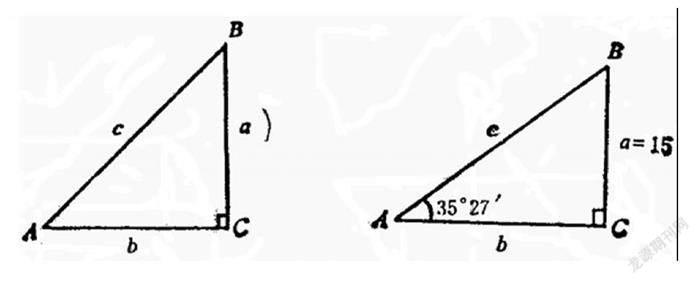
如直角三角形的边角关系：在直角三角形ABC中，有下列重要关系（如图）：

（1） 三角之间的关系：∠C90°，∠A+∠B=90°。（2） 三边之间的关系：勾股定理：a2+b2=c2。（3） 边角之间的关系：SinA=a/c，cosA=b/c，tgA=a/b，ctgA=b/a。

解直角三角形是解一般三角形的基础，因为任何一个三角形都可以分成两个直角三角形。正是通过这种联系，我们可以得到正弦定理、余弦定理。我们可以这样认为：余弦定理可以看成是勾股定理在一般三角形中的推广；而在直角三角形中，正弦定理就转化为锐角正弦函数的定义了。

四、笛卡儿关于数学思维的两个基本想法

在数学思维中，有一个共同的特点，就是要用代数的方法来解决几何问题。例如，关于三角形和圆的某些问题，因为有了三角函数与勾股定理、正弦定理、余弦定理之后，可以用代数方法来解决了。

笛卡儿在他所生活的时代里，想创造一种方法来解决所有几何问题。结果，笛卡儿实现了他的愿望，建立了今天被称之为《解析几何》的理论。

笛卡儿的成功，主要在于有两个基本想法，一是坐标概念，二是坐标方法。

在笛卡儿之前的时代，每当人们遇到含有两个未知数的代数方程F（x，y）=0时，大家都说问题的解答是不定的，由一个方程无法决定两个未知数的值，并且把这种方程Hq做“不定方程”。除了少数数学家研究“不定方程”的有关问题外，一般的人都认为这种问题不值得特别关心，例如研究整系数不定方程的整数解问题。

笛卡儿却不然，他不认为方程是“不定的”。笛卡儿开创了整整一门新的学科——解析几何学。特别重要的是，笛卡儿的解析几何为微积分理论的创立准备了条件。完全可以这样说：微积分方法的创立，如果没有解析几何的预先发展，是难以想象的。关于解析几何与微积分的具体内容我们在这里就不作叙述了。

另外，逻辑思维方法与非逻辑思维方法是数学中重要的思维方法。数学思维方法是数学思维活动必须遵守的规则，是数学思维运算获得成果的必不可少的手段。但是，數学本身还有一些重要的方法，这些方法都是数学所固有的，都称为数学方法。再者，研究、掌握数学方法还能够丰富辩证逻辑的内容。同时应该指出，在中学数学中，并不是所有问题都能够通过化归思维方法来解决的，要对具体问题进行具体分析。如何寻找正确的化归途径和怎样选择恰当的转化手段等技巧问题，是运用化归思维方法解决问题的关键。

应该说，我国中学数学界对思维的研究还处于起步阶段。对于一个具体的方法来说，我们还很难清楚地说出它的哲学基础、它的逻辑依据、它的主要功能、它的基本形式与实施程序，以及与它相关的方法链或知识链、它的教育价值等；至于数学方法的层次，则更难以理顺清楚。这都有待于我们进一步去研究、探讨并付诸实践。