练习设计助推小学生数学学习力的培养

陈友廷

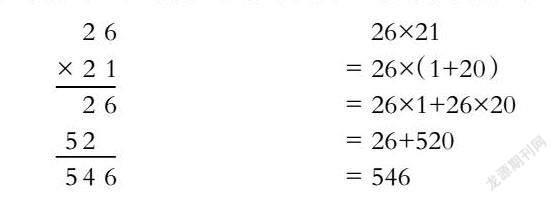
学习力是学生的知识生长能力，学习力的产生和发展过程，本质是学生的经验不断地积累和自身不断重组的内在领会。通常我们认为学习能力包括提出问题能力、认真倾听能力、表达说理能力、同伴交流对话能力、小组协作能力、解决问题能力和自我反思能力，它们互相交织、相互作用，构筑成一个庞大复杂的学习能力知识网络。从事一线教学的教师认为提升学生学习力已经是箭在弦上，但由于教学理论和经验的不够充足，对于学习力的研究更多的是停留在研究别人的理论成果上，发展学生的学习力在学校教育中如何实施，特别是怎样在教学中缺乏具体的实践和研究。从教师层面讲，一切以学生為主体；从学生层面来讲，就是要提升学生自身学习能力。练习设计可以从生活情境中提炼出数学问题，让学生知道数学知识根源在哪里。让数学回归最初生活中去，学会用数学思想和方法解决生活中的问题，从而有效提高数学学习力。

一、练习设计以“情境”为依托，挖掘数学本质培养学习力

数学是注重应用的科学，学习的最终目的是为了应用。课堂作业设计目的在于引导学生走出教室，跳出课本，以生活为教科书，让学生体会到生活中处处有数学。在实践运用中掌握和悟得一些研究解决问题的方法和策略，从而使所学知识得到拓展和延伸，让学生在领会数学价值的同时形成数学应用的意识，更喜欢去学习数学，学好数学，善于应用数学。因此，在《圆》的这一单元教完后我设计了这样的数学问题串作为课后练习。

郑耀华想给家中圆形餐桌换上一张新的桌布（桌布大小与餐桌面积一样大），他测量了下面三组数据：①将桌布对折后（完全重合）量折痕长1.4米；②沿桌子边缘一周量长是4.396米；  ③将餐布对折两次量折痕0.7米。

（1）如果你是郑耀华你会用上哪一个数据给桌子换一张崭新的桌布？说说你的道理。

（2） 郑耀华从商店一块正方形的布料上剪下这个圆形桌布，你觉得正方形的边长至少要多少米？剪下圆形桌布后剩下的布料是多少平方分米？（请你画出示意图表示）

（3） 郑耀华想在餐桌中间摆一个圆形转盘，转盘的半径大小有：①2.5分米②7.5分米③5分米的。你觉得郑耀华选哪一种比较合适？请说明理由。郑耀华家的圆形菜盘子直径是0.2米，你觉得这张转盘最多能摆下25个盘子吗？请说明理由。

生活中处处都有圆的影子，圆是平面图形中最完美的图形。本题立足于学生已有的生活经验，既有基础知识的考查，又有基本解决问题能力的考查，结合学生动手操作能力、画图能力等进行考查；做到关注数学知识模型建构，并进行合理解释和应用，充分体现学生学习力的自主发展。

（一）在探究中解决问题培养批判力

第一小题设计学生可以通过不断地折叠发现圆是对称图形，圆的大小跟直径和半径有必然的联系。知道周长可以求出半径就能确定桌布的大小。对折两次后折痕就是圆的半径，学生可以任选其中一个说明理由都是正确的。这样的设计既能使他们感悟分析和研究问题的方法，又能给学生留出了必要的探索空间。

（二）在联系中理清知识培养反思力

第二小题的设计是求组合图形的面积，先分别求正方形与圆的组合图形的面积，再求正方形的面积减去圆的面积等于剩下的布料面积，同时得到结论正方形的边长就是圆的直径。打通新旧知识的串联，使不同知识之间相辅合理解决问题，体会知识之间的应用联系。

（三）在应用中经验积累培养表达力

解决第三小题学生必须具备一定的生活经验积累与应用，能根据餐桌与转盘之间的空间大小合理进行判断，再结合计算或画图的方法解决第二个小问题，但要求学生要有一定的生活经验才能关注到圆形之间的摆放有空隙，才能合理完整解决问题。

本题围绕圆的知识设计了三个小问题，练习设计既突出了圆这一单元的基础知识、基本能力，又巩固了以前所学知识，很好地打通知识之间的联系形成系统的练习。根据不同的学习内容设计多种类型的练习，让学生真正脱离形式单一的机械重复练习。结合生活情境使练习具有趣味性，让学生在做数学作业的过程中，学会如何思考和创造性地解决问题，让学生在丰富的、有意义的作业活动中，获得丰富的学习力的发展。

二、练习设计以“说理”为载体，发展推理能力提高学习力

在“双减”背景下，为了提高数学教学质量，培养学生的数学学科素养，教师在平常的教学过程中要关注学生对知识的理解，还要求学生运用数学的知识对一些问题能够有条理地思考，比较完整地叙述思考过程，并说明理由。使学生在学习过程中对知识的掌握不但知其然，还知其所以然。数学教材中蕴藏大量的推理素材，作为一线教师要善于挖掘发现并融合到练习中，希望通过说理激发学生学习的兴趣，培养敢于创新、敢于表达、学会说理的良好学习品质，从而提高学习能力。

例如：学生学了分数的大小比较后，出了这样一道（基础练习）：箱中有6个球，分别是1号球、3号球、4号球、6号球、8号球、9号球，两个同学在做摸球游戏。（每次摸完球放回箱中）

（1） 每人摸一次，每次摸两个球。将得到的两个球数字组成一个真分数。

（2） 比一比谁组成的分数大，大的先得10分，重复做几次，看看谁先得到60分。

（3） 在比较分数的大小时你应用了哪些方法？请说明理由。

分数的大小比较经常使用的方法，学生通过通分把异分母分数转化为同分母分数再进行比较。而第3小题问题设计引发不同层次的学生不同方法的思考。学生在理解不同的比较方法中，不断地体验方法的多样性，进一步发展学习力。

学生在学习“分数的大小比较”时，教师要引导学生进行观察和比较，发现解决问题的共同要素，概括出解决问题的数学思想方法：如通过分析数量关系式来辨别使用灵活方法，通过画数轴进行数形结合来表征问题情境，通过比较，寻找参照数多元解决问题策略等等。引导学生将相同的方法运用于不同的数学问题中，在同一个数学问题中多元思考解题策略，培养学生的综合能力与概括能力。如此一来，学生在学习“分数大小比较”时，能于问题变化之中分析数量间关系的本质，构建有效的解题思路，增强方法迁移。

苏教版四年级下册乘法分配律（变式练习）中，经常用竖式来计算多位数乘法。你能结合乘法分配律解释其中的道理吗？

本题练习设计结合两位数乘两位数的算法打通乘法分配律、乘法的意义之间的关系，因此，教师在教学中要运用恰当的策略，促进学生的学习迁移，启迪学生构建系统的知识体系，发展学习力。

学生通過自己的思考：左边26乘以21在竖式计算中先用第二个乘数个位上的1去乘26表示26个一，再用十位上的2去乘26表示52个十，26个一加上52个十等于546；右边把第二个乘数21拆成20加1再分别乘26运用乘法分配律1个26加上20个26也等于546。

学生的学习力是充分建立在学生已有的认知能力基础上，通过独立思考探究“跳一跳”就能解决问题。学生思维的清晰性、深刻性和数学语言能力的发展密切相关。这道试题设计，关注如何帮助学生透过现象看本质。帮助学生理清知识的来龙去脉，揭示知识之间的内在联系，让学生理解知识的本质内涵，激发学生提出新问题，促使学生改变浅尝辄止的思维习惯，引领学生思维逐步走向深刻。

三、练习设计以突出数学“素养”为根本，拓展学生学习力

学生数学素养是一种潜移默化的过程，让学生经历了“观察、发现、举例验证、概括归纳”这样一个知识的形成过程。这样不仅让学生获得了数学基础知识和基本技能，也提高了基本能力。在教学圆的周长与面积关系时，学生可以通过课前、课中、课后反复的测量数据得到它们之间的关系，让数据说话，圆周率“π”是如何产生的？学生只有经历深入探究才能获得知识的本质。引导学生用数学思维方式去发现、去探索。使学生对周长和面积公式的推导过程能通过图文结合动手操作验证。

例如：在探究圆周率过程中设计这样一道练习：和数学家们一起探秘圆周率实验单。

实验记录员：

实验目的：你能求出圆周率吗？

实验方法：把探秘圆周率的方法记录下来。

实验要求：可以独立完成也可以找同学合作完成，但数据必须真实有效，操作过程要有科学依据。

实验思考或困惑：在尝试过程中阅读圆周率历史进程，写一写你的困难再与同学交流。

本道练习设计通过学生动手操作实验，学生小组合作收集数据、整理数据对比观察，既凸显了数学知识的本质，丰盈了学生对数的感觉，同时又考查了学生的数学阅读能力，培养学生的数学素养，感受数学文化的博大精深。进一步提高学生的合作能力、探究能力；发展空间观念、应用意识和探究意识。通过练习打开学生的思路、拓展学生的视野，促进不同学生能力的发展。使学生经历认识圆周率的历史进程，进一步丰富对现实世界中数量关系的认识，体会不同部分数学知识之间的联系，获得解决问题的策略，培养初步的形象思维和逻辑思维能力。

学生所有的学习力最终表现在解题、析题中，因此，作为一线教师要明确练习目的，要做到练习“为什么练”“练什么”“怎么练”“练得怎样”，在课前、课中、课后设计习题时有的放矢。

综上所述，课程目标以发展学生为本，以核心素养为到导向，小学数学新课标经历了从强调“双基”到“四基”关注基本思想和基本活动经验。数学练习是一种学习活动，也是学生学习力的一种体现。因此，我们在平时教学设计中的试题要有效激活学生思维，促进学生积极思考，提升思维品质。关注“立德树人”的教育功能、数学核心知识的理解、数学思维品质的提升等。坚持以学科核心素养为导向，通过“情境”“素养”“说理”等在命题练习中的定位及相互联系。让学生通过练习真切体会数学到在实际中的应用，更进一步地培养学生学习的迁移学习能力。