Current-Aided Multiple-AUV Cooperative Localization and Target Tracking in Anchor-Free Environments

Yichen Li,, Wenbin Yu,, and Xinping Guan,

Abstract—In anchor-free environments, where no devices with known positions are available, the error growth of autonomous underwater vehicle (AUV) localization and target tracking is unbounded due to the lack of references and the accumulated errors in inertial measurements.This paper aims to improve the localization and tracking accuracy by involving current information as extra references.We first integrate current measurements and maps with belief propagation and design a distributed current-aided message-passing scheme that theoretically solves the localization and tracking problems.Based on this scheme, we propose particle-based cooperative localization and target tracking algorithms, named CaCL and CaTT, respectively.In AUV localization, CaCL uses the current measurements to correct the predicted and transmitted position information and alleviates the impact of the accumulated errors in inertial measurements.With target tracking, the current maps are applied in CaTT to modify the position prediction of the target which is calculated through historical estimates.The effectiveness and robustness of the proposed methods are validated through various simulations by comparisons with alternative methods under different trajectories and current conditions.

I.INTRODUCTION

THE rapid development of underwater-vehicular technologies has enabled the widespread use of autonomous underwater vehicles (AUVs) in marine applications [1].In most cases, the completion of tasks is based on the known positions of the AUVs and the target.Thus, AUV localization and target tracking are both fundamental technologies underwater and they provide continuous position estimates respectively for the own AUVs and the target of interest.However,due to the lack of the global positioning system, harsh communication conditions, complex underwater environments,etc., underwater localization and tracking have always been challenging problems [2].Usually, the AUVs’and the target’s positions are estimated with the help of the anchors, i.e.,devices with known positions.Typical examples are baseline systems [3].However, owing to the limited coverage of currently deployed devices, anchor-free environments commonly exist, such as the mid-depth ocean [4] and ice-covered regions[5].In the above scenarios, without the assistance from anchors, the target tracking should be carried out by AUVs whose positions play as references in the tracking.Generally,AUVs can localize themselves with inertial measurements using dead-reckoning (DR).However, due to the lack of position references and the accumulated errors in inertial measurements (termed accumulated errors hereafter), localization errors grow without bound [6] and accordingly reduce tracking performance.Thus, in anchor-free environments, AUV localization and target tracking are heavily coupled and should be considered together.

In anchor-free environments, cooperation among AUVs could be a solution to improve localization and tracking accuracy [7].In previous works [8]–[11], many cooperative localization and tracking methods are designed and have verified the effectiveness of cooperation.Among them, belief propagation (BP) [12] is a widely-used cooperative framework.Its extensions [13]–[15] are constantly designed to enable BP applicable to nonlinear non-Gaussian situations.Moreover, it is naturally distributed and with good scalability.The above features make BP suitable for cooperative localization and target tracking problems [16]–[18].However, in most previous works, accuracy improvements are based on the assistance from anchors.Considering the coverage of the deployed anchors is limited and anchor nodes are easy to fail due to the harsh underwater environments, studies of the anchor-free localization and tracking are still needed.

Without anchors to bound the error growth in anchor-free environments, the accumulated errors would greatly degrade AUV localization accuracy.In previous works, the lack of a specific design for the accumulated errors puts their usability into question.In [19] and [20], the proposed methods attempt to solve the problem with neural networks and terrain-aided designs, while only single-AUV localization is considered.The works in [5] and [21] mitigate the misleading nature of the accumulated errors by simulating the uncertainty accumulation in the position prediction.In [22], the accumulated errors are further compensated by their own estimated values using historical localization results.However, the above methods are still based on the direct use of raw inertial measurements and the accuracy improvement is limited.As for target tracking, since AUV localization and target tracking are coupled in anchor-free environments, tracking accuracy is sensitive to the localization.The work in [22] investigates both of them.However, the error growth in AUV localization seriously affects the accuracy improvement of target tracking.In[23], the relationships between localization and tracking in different scenarios are discussed.However, no newly effective solution is proposed.Moreover, the noncooperative nature of target also increases the difficulties of tracking.Existing methods usually assume the target’s state-transition function is known, which is not appropriate in practice.In [24]and [25], model-free prediction methods are designed to approximate the speeds and heading angles with former estimates and evolve target positions with DR principles.The aforementioned works indeed improve localization and tracking performance.However, due to the insufficient information in anchor-free environments, the improvement by modifying the use of available measurements would be limited.Under such circumstances, trying to bring in extra reference information may be a viable option.

Since ocean currents are ubiquitous underwater and, with the development of the ocean general circulation models(OGCMs), currents can be forecasted with high resolution[26], designing current-aided methods have potential in anchor-free environments.Usually, ocean currents are considered as disturbances that degrade the performance of algorithms [27], especially in target tracking [28] and [29].Recently, based on the predicted current maps, the idea of introducing currents as auxiliary information has been studied in trajectory planning [30], flock guidance control [31], etc.In AUV localization, previous current-aided methods are mainly designed for single-AUV localization.In [32], the proposed method uses current information to improve the performance of the inertial navigation system, and the use of current in [33]only considers the localization during the descent of an AUV.In [21], a current-aided method is designed as a complement to cooperative localization when the AUV team remains silent.A current-aided cooperative navigation scheme named flow-aided cooperative navigation (FACON) is proposed in[4].However, the current-aided navigation therein is performed individually for each AUV, and the cooperation among AUVs is designed in an opportunistic fashion.As a result, methods that are able to internally integrate current information with AUV cooperative localization and target tracking are in urgent demand.

In this paper, based on BP, we investigate multiple-AUV(multi-AUV) cooperative localization and target tracking with the assistance of ocean currents.The comparisons between this work and the aforementioned typical works are displayed in Table I, and our contributions are summarized as follows:

1) We involve the current measurements and maps with BP and propose a current-aided BP message-passing scheme,which lays the theoretical foundation for solving both localization and tracking problems with current information.Under the scheme, current-aided cooperative localization (CaCL)and current-aided target tracking (CaTT) algorithms are designed and realized by particles.

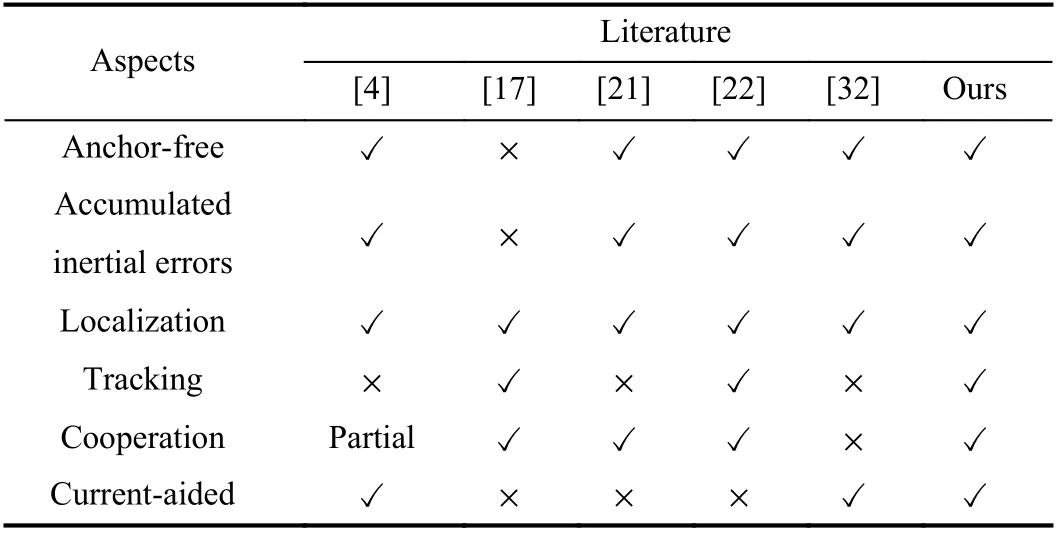
TABLE I THE COMPARISONS BETWEEN THIS WORK AND TYPICAL ONES

2) To alleviate the localization error growth caused by the accumulated errors, CaCL improves the localization using cooperation among AUVs.Moreover, it modifies the AUV position prediction and the relative position representation assisted by current measurements and maps.In this way, the quality of the predicted and transmitted information of each AUV is improved, and higher localization accuracy is achieved accordingly.

3) A model-free prediction process assisted by current information is designed for noncooperative target tracking in CaTT and consists of two parts.The first part is calculated with historical estimates and current maps, and the second part is obtained by particle random evolvement.Such a design stably improves tracking accuracy and provides CaTT with good adaptability to different target motions and map qualities.

The rest of this paper is organized as follows.The problem statement and the system models are presented in Section II.We integrate current information with BP in Section III.The proposed localization and tracking algorithms are introduced in Sections IV and V, respectively.The simulations are described in Section VI, and the conclusions are drawn at last.

Notations:The variables and particles are presented using bold and Roman letters (e.g.,xand x), respectively.The sets of variables are denoted by capital letters (e.g.,X).The hats on the letters indicate they are either measurements or estimates.Both variables and particles have different superscripts and subscripts, which are listed in Table II.

II.PROBLEM STATEMENT AND SYSTEM MODEL

A.Problem Statement

In this article, we investigate multi-AUV cooperative localization and target tracking assisted with current information in anchor-free environments.Fig.1 shows a typical example of the anchor-free environment, where target tracking is carried out by AUVs and AUVs play the role of both task performers and position references, which allows for target tracking to be based on AUV localization.However, without the assistance from anchors, the error accumulation in inertial measurements would seriously influence localization and tracking accuracy.Since ocean currents are ubiquitous and can be measured with acoustic Doppler current profilers (ADCPs), it hasthe potential to be applied as an extra reference to assist localization and tracking in anchor-free environments.Furthermore, high-resolution current maps are available nowadays with OGCMs and can be uploaded to AUVs before their deployment, which further lays the foundation for the development of current-aided methods.

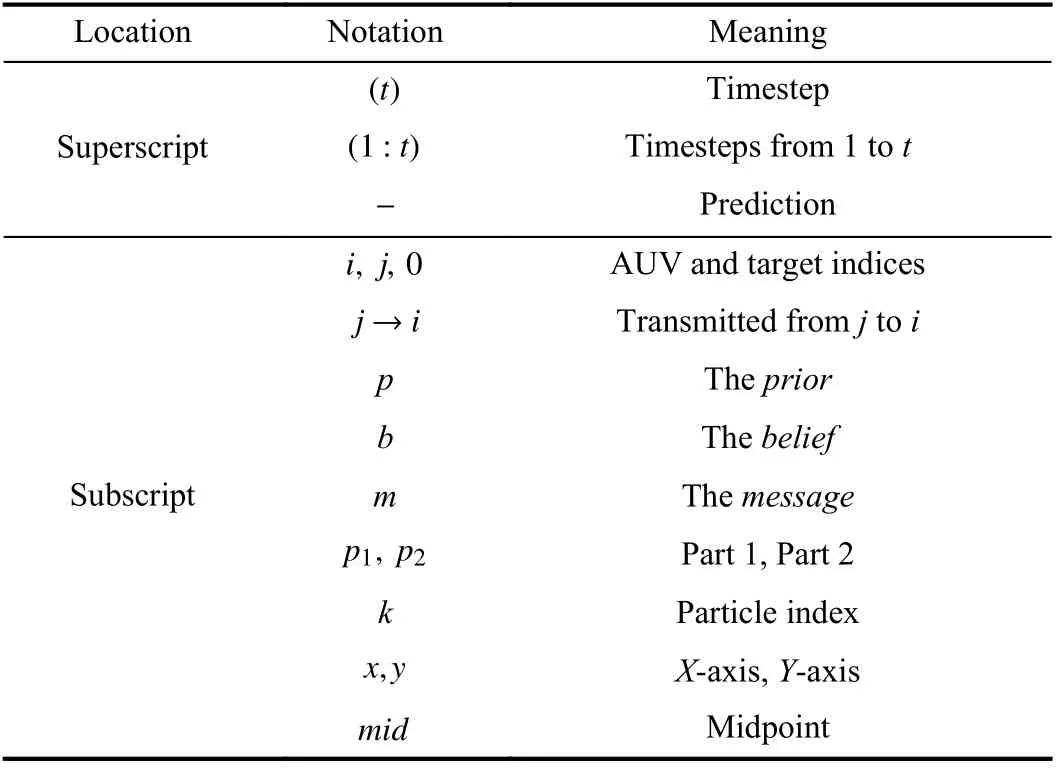
TABLE II SUPERSCRIPTS AND SUBSCRIPTS

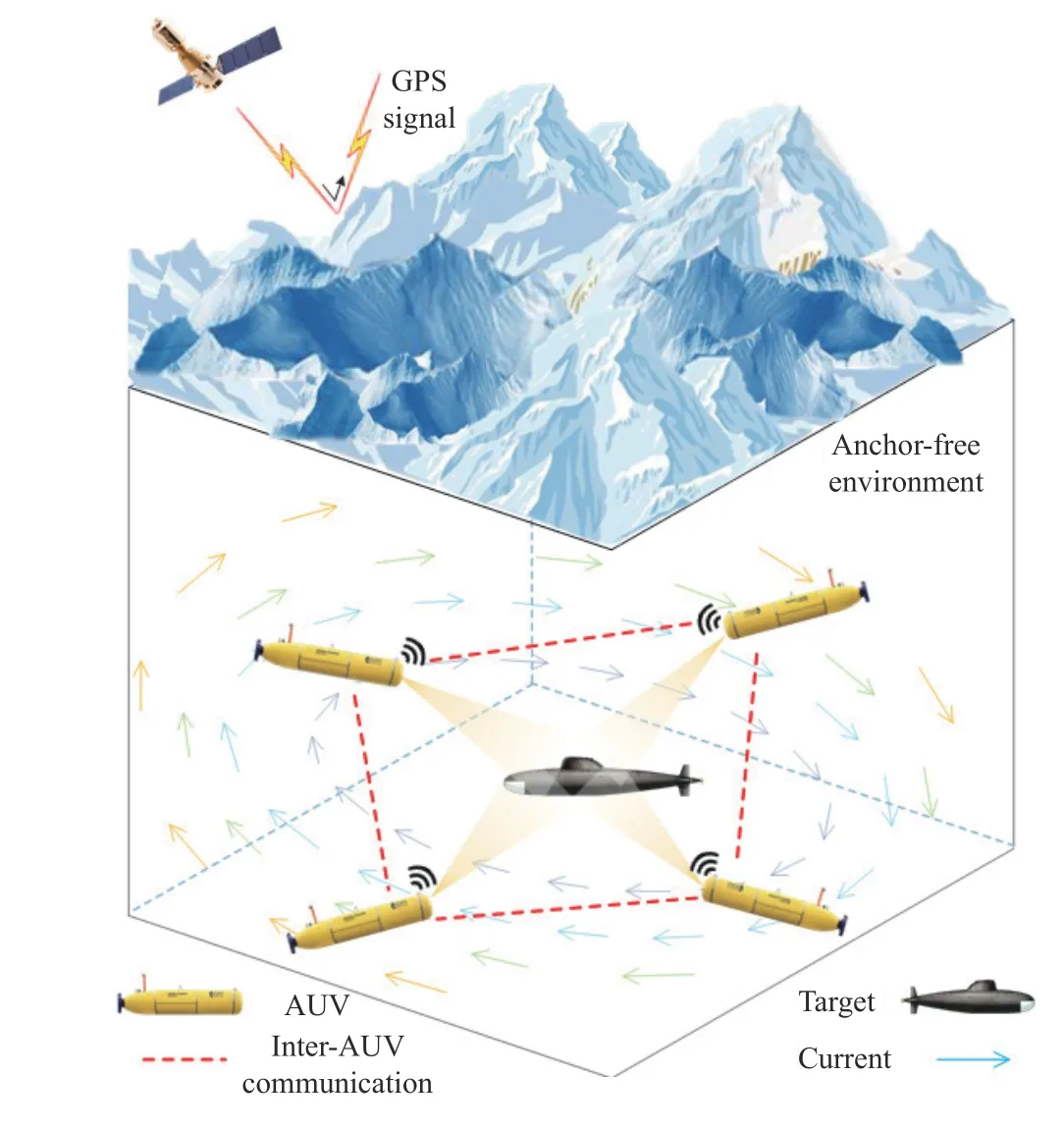
Fig.1.An ice-covered anchor-free environment.

Thus, different from the previous works that mainly focus on single-AUV problems, this paper aims to improve the performance of both the multi-AUV cooperative localization and target tracking using current information without the help of anchors.Note that, the so-called current in this paper is not limited to ocean currents, and it could be any known flow field as long as predicted maps can be obtained.This also allows for current-aided methods to have broad application potential.

B.System Model

Note that, in this paper, the proposed algorithms are realized by particles and could be applied to various noise models.Since the inter-AUV measurements are usually time-ofarrival-based (TOA-based) and the noises can be assumed Gaussian [37], to unify noise models, we assume that the aforementioned noises are zero-mean Gaussian with variances already defined.Moreover, to implement TOA-based measurements, we assume all the AUVs are synchronized.To fulfill the models defined above, we assume AUVs are equipped with IMUs, ADCPs, depth sensors, and ranging devices.All of them are standard for AUVs [6].Moreover, we also assume the cooperation among AUVs is based on acoustic communications which are achieved by the equipped communication modems.The used protocol could be the time division multiple access or other equivalents.A device suite that has been validated through sea trails can be found in [38].

III.CURRENT-AIDED BP MESSAGE-PASSING SCHEME

In this section, based on current information, we first establish the interrelated structure of AUV localization and target tracking using a factor graph.Then, by combining the BP message-passing scheme with the factor graph, we build the current-aided BP message-passing scheme, under which localization and tracking algorithms are designed and will be introduced in Sections IV and V, respectively.

The multi-AUV cooperative localization and target tracking problems can be mathematically viewed as state estimations.Under the Bayesian framework, localization and tracking can be achieved given prior information and measurements.A commonly used Bayesian estimator, named the minimum mean squared error (MMSE) estimator [39], is written as (8)

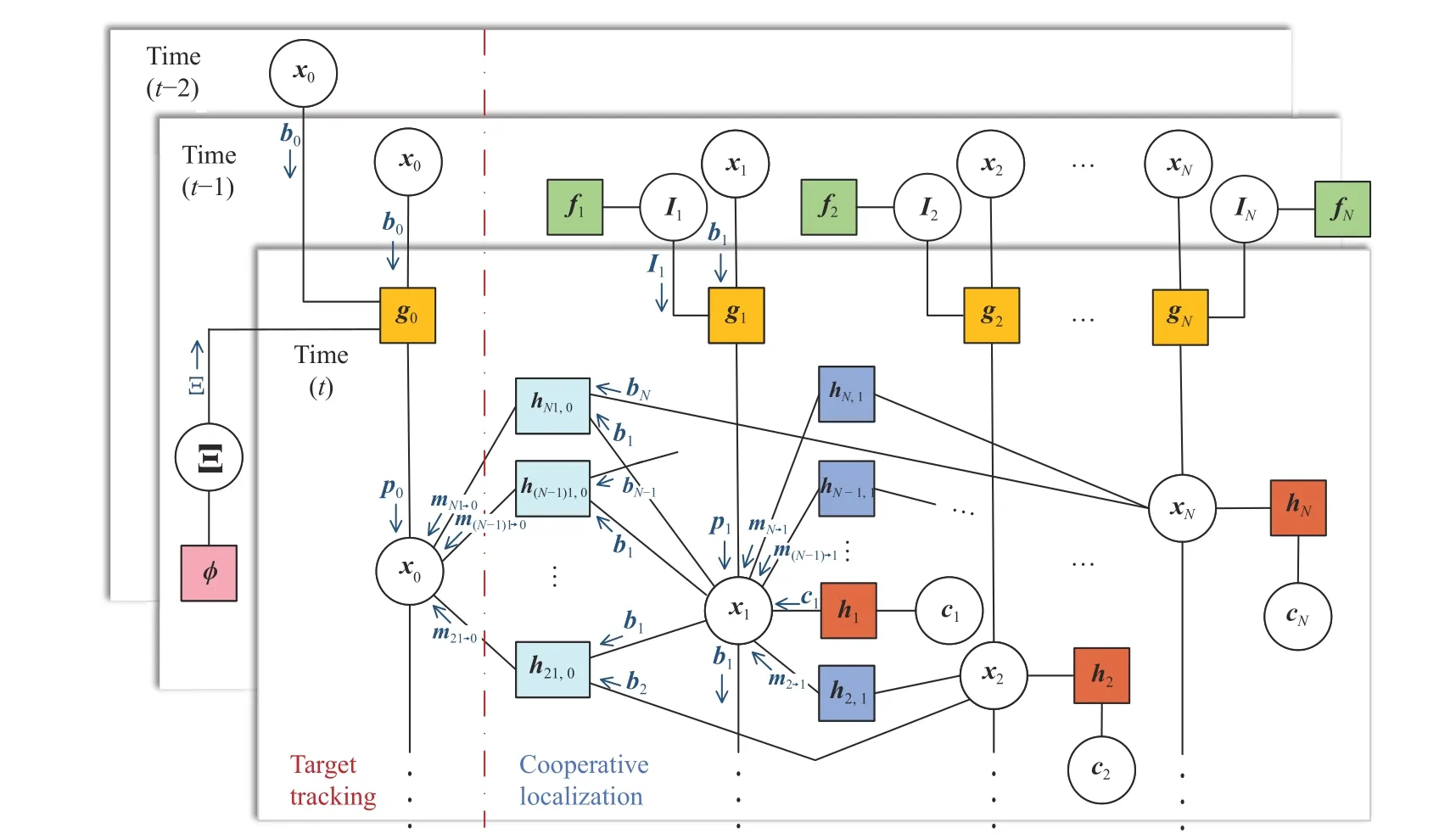
Fig.2.The factor graph of the current-aided BP message-passing scheme: Information of different timesteps transmitted along the factor graph to achieve cooperative localization and target tracking.Abbreviations: g0≜p(),gi≜p(), h j,i≜p(),h ji,0≜p(,), fi≜p(),hi≜p(), ϕ ≜p(Ξ(t)), b0≜(),bi≜(),p0≜(, pi≜)(), mj→i≜m) and mji→0≜()), fori,j∈A,i≠j.

With thepriorand themessages, the calculation of thebeliefcan be achieved through multiplication.

In anchor-free environments, AUVs are the position references in target tracking, which makes AUV localization and target tracking heavily coupled and the tracking accuracy is sensitive to localization.Based on the factor graph in Fig.2 and the above-defined terminologies, the proposed currentaided BP message-passing scheme unifies the cooperative localization and target tracking into one calculation framework and specifies the theoretical principles for their realizations.It is summarized in Algorithm 1, where the head AUV is assigned to fuse the target information and will be introduced in Section V.Usually, localization and tracking can be performed in parallel or serially.Considering the fact that the target tracking accuracy in our problem is relatively low due to the lack of anchors, higher overall accuracy could be obtained through the serial execution of localization and tracking [23].As a result, AUV localization is performed before target tracking at each timestep in Algorithm 1 and serves as an accuracy guarantee of the position references when tracking the target.

Based on the proposed message-passing scheme, particlebased localization and tracking algorithms are respectively designed in the following sections.The reasons for the use of particle realizations are threefold.

1) Particle-based methods could be applied in nonlinear non-Gaussian problems.The characteristics of not being restricted to Gaussian models make the designed algorithms enjoy adaptability to the complex underwater environments,which guarantees a wide range of applications.

2) In our problem, due to the nonlinear and potentially non-Gaussian models, the closed forms of the integrals in (12) and(13) are difficult to obtain.By using particle representations,the complex integrals can be avoided.

3) Particle-based methods can provide position estimates as well as the representations of estimation uncertainties, which provides a reliability measure [40] and further improves the environmental adaptability.

Note that, based on the information flow in Fig.2 and the BP message-passing principles, each AUV should generate differentmessagesand transmit them to the corresponding neighbors one by one.Such is inefficient for communication and unfriendly in the energy-limited underwater environments.To reduce the communication consumption in the proposed scheme, at each timestep, AUVs only broadcast theirpriorsonce and themessagesare generated locally at the neighbors.The details of this trick can be seen in [40].

Algorithm 1 Current-Aided BP Message-Passing Scheme 1: Time 2: \* Cooperative localization: CaCL in Section IVi=1t=1,2,3,...3: AUVs to Nin parallel:4: Generate the prioraccording to (11)5: Broadcast the priorand measure the inter-AUV 6: distances with the neighbors 7: Generate the messageswith the received priorand the 8: inter-AUV distances according to (13)9: Calculate the beliefwith the obtained priorand 10: messagesaccording to (10)11: Obtain the AUV’s position estimate by (8)12: end parallel 13: \* Target Tracking: CaTT in Section Vi=1 14: AUVs to Nin parallel:15: Measure the TDOA measurements of the target 16: Transmit the beliefand the measurements to the 17: head AUV 18: end parallel 19: The Head AUV:20: Generate the target’s prioraccording to (15)21: Generate the messageswith the received beliefsand 22: measurements according to (16)23: Calculate the target’s beliefwith the obtained prior24: and messagesaccording to (14)25: Obtain the target’s position estimate by (8)26: end 27: end time

IV.CURRENT-AIDED COOPERATIVE LOCALIZATION

Based on the current-aided BP message-passing scheme, we propose a particle-based current-aided cooperative localization (CaCL) algorithm to help the AUVs alleviate the impact of the accumulated errors and improve localization accuracy.Considering the fact that speeds could be measured with high accuracy and major localization degradation is caused by the heading angle measurement errors [34], CaCL mainly focuses on dealing with the accumulated errors in the heading angles.

From Algorithm 1, the key to CaCL is the generation of theprior, themessageand thebelief.The illustration of the whole particle-based process of CaCL is shown in Fig.3.According to the Bayesian theory, the basic idea behind CaCL is to generate a properpriorand correct it with themessages.From the perspective of particles, CaCL generates particles of thepriorwith the assistance of current information and reweighs them with themessages.As a result, the particles near the AUV’s true position would obtain high weights and dominate the localization result.For this reason, in the design of theprior,we would like to obtain as many particles as possible close to the AUV’s true position.The bottom line is, in harsh conditions (with large localization errors), to ensure the coverage of thepriorcontains the true position so that the particles near it can be picked out by the subsequent correction (reweighing)process.

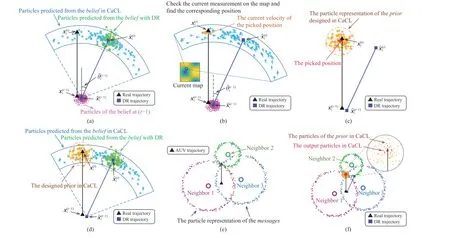
Fig.3.The illustration of CaCL.(a) Particle prediction; (b) Map check; (c) Priorgeneration; (d) Priorcomparisons; (e) Messagegeneration; (f) Beliefcalculation.

In the following, we would introduce thepriorgeneration[Figs.3(a)−3(c)], themessagegeneration [Fig.3(e)], and thebeliefcalculation [Fig.3(f)] in CaCL.

A.The Prior Generation

Intuitively, the particles of the designedpriorare nearer to the true position of the AUV.According to the logic stated at the beginning of Section IV, more particles close to the true position pave the way for the good localization accuracy,which will be explained in Section IV-C.

B.The Message Generation

C.The Belief Calculation

V.CURRENT-AIDED TARGET TRACKING

According to Algorithm 1, target tracking is carried out after the AUVs have completed their localization.In this section,we deliver the proposed particle-based current-aided target tracking (CaTT) algorithm.Under the current-aided BP message-passing scheme, the logic behind the design of CaTT is similar to that of CaCL.Theoretically, the target’spriorand themessageare still the keys to the tracking.However, the noncooperative nature of target makes the generation of them different from those in CaCL.Moreover, since the target cannot locally process the information, in target tracking, the measurements are gathered and calculated at a certain AUV,named the head AUV.

A.The Prior Generation

Form (40) we can see that the particles of the second part evolve randomly towards all directions and cover a larger area compared to that of the first part.In this manner, the second part can be regarded as the supplement to the first part and improves the tracking performance from the following three aspects:

1) Since the first part of thepriorrelies on previous tracking estimates, its effectiveness can be easily degraded by the tracking and localization accuracy, especially when AUV localization errors grow large.To improve the robustness of CaTT, the second part guarantees theprior’s coverage of the target’s true position, so that the lower limit of tracking accuracy is assured.

2) Similar to the first aspect, the first part of theprioris obtained based on current maps.When the maps are of poor quality, the prediction would deviate from the target’s true position.Under such circumstances, tracking accuracy is still guaranteed by the second part, which improves the adaptability of CaTT to different map qualities.

3) The target’s noncooperative nature not only makes it difficult to obtain the state transition information but also potentially leads to its high mobility to avoid being tracked.If the target’s trajectory (motion) changes quickly, the speeds and heading angles approximated from previous estimates may provide outdated movement information and mislead the particle evolvement in the first part.Under such circumstances,the second part covers all the directions the target may turn to and accordingly guarantees tracking accuracy.

B.The Message Generation

Since the target is noncooperative, TDOA measurements can be applied to denote the relative position information between the AUVs and the target.In CaTT, the head AUV first emits a signal.Other AUVs receive the signals reflected from the target and record the arrival times.Then, with the arrival times gathered at the head AUV, the TDOA measurements can be obtained through (5).

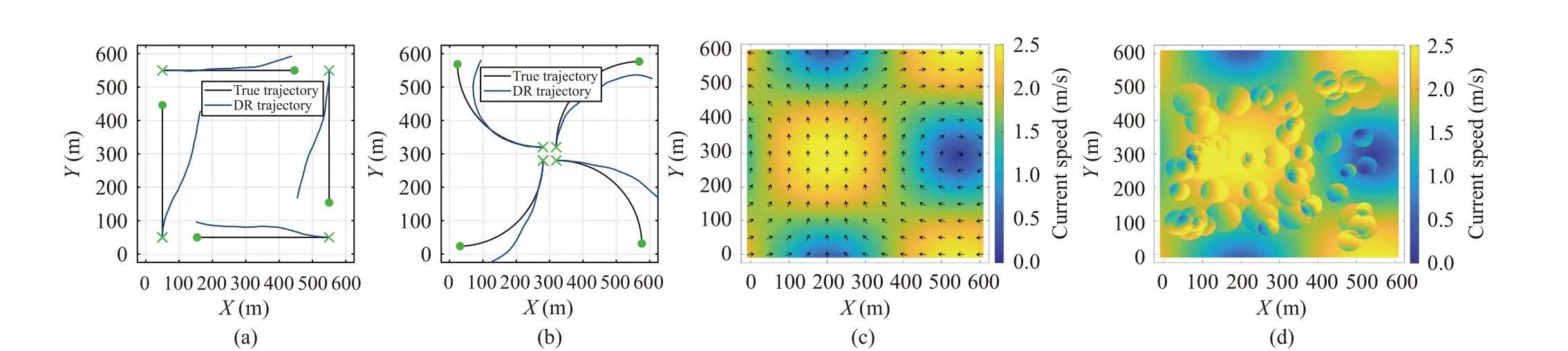
Fig.4.The simulation scenarios.(a) Straight trajectories; (b) Scattered trajectories; (c) Current map; (d) Current map with vortices.

The particles generated from (41) form a half leaf of a hyperbola on which the target lays and theith AUV is the focus of this half leaf.The use of the half leaf allows for the particles to not need to be distributed on the other half with no target and, therefore, improves the efficiency of particle utilization.

Similar to CaCL, after the generation of thepriorand themessages, the target’sbeliefand position estimate could be calculated as in Section IV-C.

C.Discussion

So far, we have completed the introduction of the proposed CaCL and CaTT methods.To further discuss the issues with respect to their practical uses, we comment here.

1) Map Quality:Since the proposed methods rely on the predicted current maps, map quality would affect localization and tracking performance.As illustrated in [32], a sequence of time-tagged current maps generated by OGCMs would be preloaded on the AUVs to support the execution of current-aided methods during navigation.However, due to the complex underwater environment and the temporal and spatial resolution of the maps, determining how to maintain localization and tracking accuracy when map quality degrades is the key to algorithm design.In the proposed methods, the use of thebelief uncertaintyin (21) and the design of the second part of thepriorin (38), respectively in CaCL and CaTT, alleviate the impact of the uncertainties in the maps by enlarging the particle coverage, preventing large accuracy drops even when current maps are of poor quality.Simulations in Section VI have validated the robustness of the proposed methods by adding unpredictable vortices in the navigation scenarios.

2) Measurement Noises:By using ADCPs, the currents relative to the AUV at different depths could be measured according to the principles of Doppler shift.With the velocities of the AUVs, ambient current measurements can be obtained.With the development of ADCPs, measurement noise could be reduced to 1 % of the measured value [44] and the measurement uncertainty in [32] is within 0.005 m/s based on the field test data.In the designed methods, current measurements are mainly used to obtain the predicted positionxˆ(i−,t)in (19) of CaCL and the effect of the measurement noises can be mitigated by thebelief uncertaintyapplied in (21) and shown in Fig.3(c).Considering the fact that the proposed methods are current-based, their performance would be affected by the uncertainties of the current in practice, including the measurement noises and the map quality discussed above.Since they are both considered in the design, CaCL and CaTT can still provide certain performance guarantees even in poor conditions.In Section VI, their adaptability is analyzed and validated through various simulations.

3) Computational Costs:Since CaCL and CaTT are designed based on the message-passing scheme proposed in Section III, they have inherited the advantage of low computational costs that grow linearly with the network size.However, due to the particle realization, thebeliefcalculation(multiplication) in Section IV-C would lead to quadratic computational growth with the number of particles [14].Considering that only the standard particle-based multiplication is applied in the proposed methods, the computational growth could be further reduced to be linear with the multiplication described in [17].Moreover, even with the quadratic computational growth, the usability of the particle-based processing has been verified through experiments with a computer commonly used for AUVs [45].In this paper, experiments with different numbers of particles are delivered to validate that the computational burdens of CaCL and CaTT would not influence their real-time processing.

VI.SIMULATION RESULTS

In this section, we validate the proposed current-aided methods with numerical simulations.The CaCL and CaTT algorithms are evaluated by various comparisons with alternative methods under different trajectories and current conditions.

A.Cooperative Localization

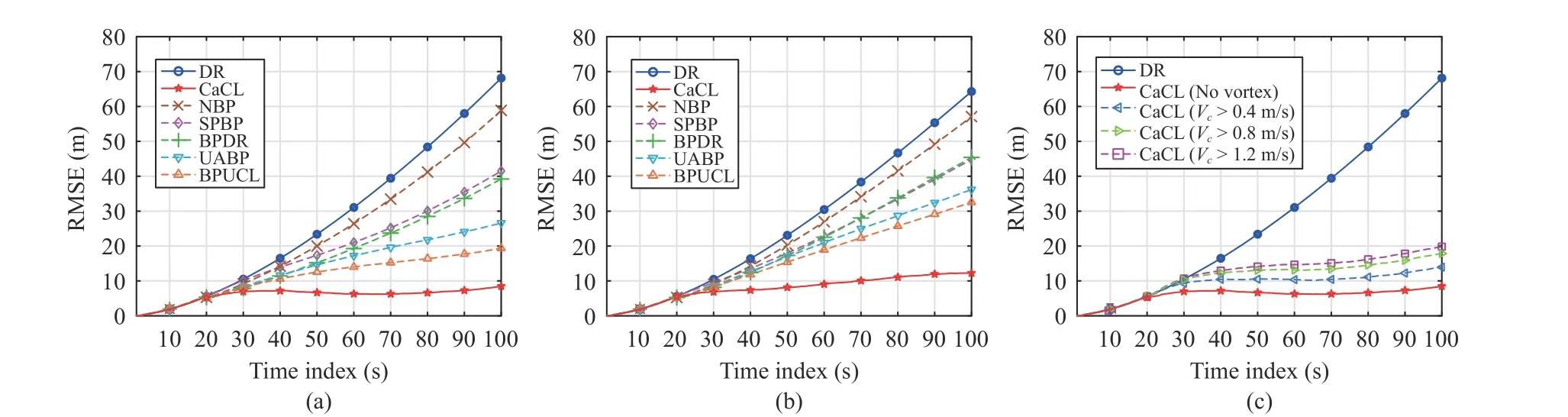
Fig.5.The RMSE results.(a) Straight trajectories; (b) Scattered trajectories; (c) With different vortex speeds.

The results are shown in Fig.5.Since the inertial navigation (DR) is able to guarantee localization accuracy in a short time, the cooperation among AUVs begins at the 2 0th second.From Figs.5(a) and 5(b), we can see that the RMSE of DR grows to around 70 m due to the accumulated errors in inertial measurements, while the proposed CaCL always provides the best localization accuracy.Moreover, CaCL is less susceptible to the influence of different trajectories.The reasons are as follows.In the results, nonparametric BP (NBP) [15],sigma point BP (SPBP) [14] and BP-based DR (BPDR) [5]are much less effective when dealing with the accumulated errors.It is because that, in the design of NBP and SPBP, the influence of the accumulated errors are not considered.BPDR uses Gaussian distributions on the predicted positions to alleviate the impact of the errors.However, the coverage of theprioris limited and BPDR performs poorly when the errors become large.The underwater-adaptive BP (UABP) [21] and BP-based underwater cooperative localization (BPUCL) [22]algorithms can provide more improvements on localization accuracy.In UABP, theprioris generated in a similar manner to the first stage of that in CaCL.By enlarging the coverage of theprior, the decline of localization accuracy is alleviated.Nevertheless, UABP directly uses inertial measurements and is still inevitably misled by the accumulated errors therein.Based on UABP, BPUCL brings in compensations to the heading angle measurements to reduce the value of the errors, and further improves localization accuracy.In anchorfree environments, the unbounded error growth in localization is due to the lack of localization references.Thus, CaCL improves localization accuracy from another perspective by involving extra references.Without the pre-deployed anchors,CaCL introduces ocean currents as the reference by integrating current information into the BP message-passing scheme.As described in Section IV, the current-aided generation of thepriormakes most particles distributed around the true position.The modifications in theprioralso improve the quality of themessagestransmitted to neighboring AUVs.In this way, CaCL provides better localization accuracy compared with the others.Moreover, as in Fig.4(a), the distances among AUVs are maintained in a similar level, while the distances increase with time in Fig.4(b), which leads to the faster RMSE growth in Fig.5(b).However, since the current references in CaCL covers all of the 600×600 m2region and would not be affected by the inter-AUV distances, CaCL reveals better robustness to different trajectories.

In current-aided methods, good performance is usually sensitive to the quality of the current map.Fig.5(c) has shown the performance of CaCL in different vortex turbulence,whereVcis the maximum speed of a single vortex.From the results, the decrease in current map quality indeed affects the localization.However, the performance degradation is limited and the accuracy is still better than the alternative methods even in harsh environments (Vc＆gt;1.2 m/s).

To further validate the scalability of CaCL, Fig.6 shows the execution time of different methods recorded by MATLAB with an Intel i7-10710U CPU.From the results, the time consumption grows linearly with the number of neighbors |Ni|,which is in accord with the linear computational growth claimed in Section III and guarantees the scalability of CaCL.However, compared with SPBP, the time consumption of the particle-based UABP and CaCL is obviously higher, especially when the number of particlesKgrows.Fortunately,compared with the long propagation delay of underwater communication (usually on the order of seconds), the execution time of CaCL is still small and would cause limited impact on the localization.Considering the accuracy improvement and the computation ability of modern CPUs, such a computational burden would not influence the usability of CaCL.To further validate its real-time processing, CaCL is deployed on a Raspberry Pi (RPi) which is widely used for entry-level AUVs.The tested RPi has a 1.4 -GHz 64-bit quad-core processor, and the time consumption has been summarized in Table III, where the longest execution time is only0.357 s under the condition of 8 neighbors and 8 00 particles.

B.Target Tracking

Fig.6.The execution time of different algorithms.

TABLE III THE EXECUTION TIME OF CACL

In this subsection, the proposed CaTT algorithm is evaluated.We first validate the designedprior(DP) under various conditions and then compare the tracking performance between CaTT and alternative methods.The scenarios are demonstrated in Figs.7(a)−7(d), where the target speed is 4 m/s.In the first two scenarios, target tracking is performed by anchors, each of which is randomly distributed in a 100×100m2region with the uncertainty of 1 0 m2.In these scenarios, the tracking performance would not be influenced by the growing AUV localization errors.Moreover, the target trajectory in Fig.7(a) is relatively flat while it has high mobility in Fig.7(b).The adaptability of DP with different trajectories could be tested in this way.In Figs.7(c) and 7(d), target tracking is carried out by AUVs, whose position accuracy decreases due to the accumulated errors.The settings of the AUVs are the same as those in Section VI-A.Corresponding to Figs.7(a)−7(d), the RMSE results are shown in Figs.8(a)−8(d).The referenceprior1 (RP-1) and 2 (RP-2) are the first and second parts of DP and calculated by (31) and (38),respectively.

In Fig.8(a), DP, RP-1 and RP-2 are compared under different current map qualities, where the map is shown in Fig.4(c)and disturbed by vortices.From the comparisons, since RP-2 applies neither the target’s previous movement information nor the current map, it provides the worst performance when it is solely used.Due to the assistance from current map, RP-1 provides better but still unsatisfactory tracking accuracy compared with RP-2.As in (34) and (35), the speed and heading angle used in the generation of RP-1 are calculated with previous position estimates, which causes the obtained speed and heading angle to contain accumulated errors and hence affects their reliability.Moreover, since the current velocity from the map used in the generation of RP-1 is based on the position estimate at the last timestep, the reliability of the obtained current velocity is also degraded with tracking accuracy.Furthermore, when the map’s quality becomes worse, the performance of RP-1 drops obviously.On the contrary, DP always provides the best tracking accuracy.Even when the current map is corrupted by vortices, the performance degradation is little.This is because DP uses RP-2 as a complement of RP-1 and combines the advantages of both.While relying on current information, it also strengthens its robustness to current interference.Fig.8(b) shows the tracking results when the target moves with high mobility.The highest mobility part of the target trajectory and the corresponding tracking accuracy of RP-1 are painted in orange in Figs.7(b) and 8(b), respectively.The poor performance of RP-1 further proves that its sole use lacks robustness when the target trajectory changes with high frequency.In the meantime, the stable low RMSE of DP indicates strong reliability.In Figs.8(c) and 8(d), the target tracking results are based on different AUV localization errors.The results show that DP still provides the best tracking accuracy.Moreover, we can also see that the localization errors would obviously accelerate the growth of the tracking errors.

Fig.9 demonstrates the target tracking accuracy comparisons between different tracking algorithms.The noncooperative mobile target tracking (NcMTT) algorithm is proposed in[22] and the consensus-based tracking (CBT) method is designed in [49].Both of them are designed for cooperative target tracking.From the comparison results, the proposed CaTT algorithm provides the best tracking accuracy no matter what localization method is used.Similar to CaTT, thepriorof NcMTT is also designed with two parts, while the lack of the assistance from current makes its performance worse than that of CaTT.In the design of CBT, the position evolvement function is assumed known, which is impractical in real-world applications.In the comparisons, thepriorof CBT is generated similar to (31) using the speed and heading angle calculated through (34) and (35), respectively, with Gaussian uncertainties.The lack of the current assistance and the uncertainty approximations make the target tracking of CBT less accurate.Moreover, we also simulate the CBT tracking with DP and it results in almost the same performance as CaTT.However, since consensus-based algorithms usually require multiple iterations of communication through the network to make the algorithm converge, the communication cost is large.In underwater scenarios, unstable communication and limited energy make the implementation prospects of consensus-based algorithms slim.The results in Fig.9 also show that localization accuracy lays great importance on tracking accuracy.With better localization accuracy, the performance of the tracking methods is improved.Thus, since the proposed current-aided algorithms provide the best performance respectively in localization and tracking, the combinational use of CaCL and CaTT improves tracking accuracy as much as possible.In addition, we can also see that, with the increase of the localization error, the performance gaps between different tracking methods are smaller.It is because that large localization error degrades tracking accuracy and limits improvements, which further illustrates the importance of improving localization accuracy.

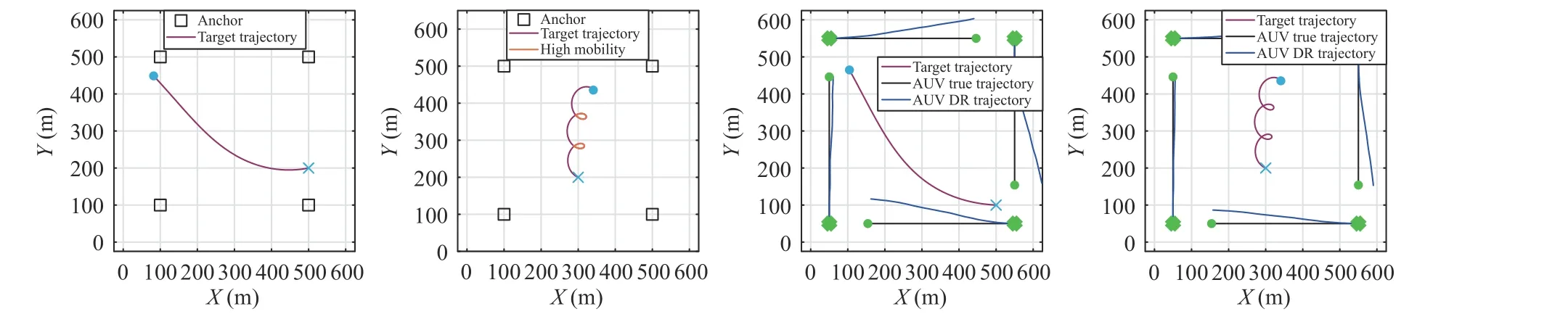
Fig.7.The target tracking scenarios.(a) Tracking with anchors; (b) Tracking with anchors (high mobility); (c) Tracking with AUVs; (d) Tracking with AUVs(high mobility).

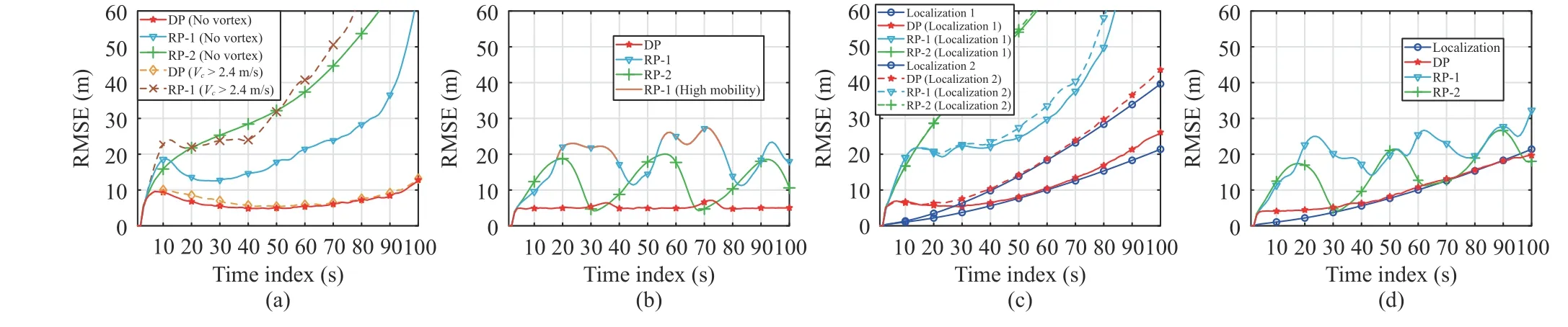
Fig.8.The target tracking results.(a) Tracking with anchors; (b) Tracking with anchors (high mobility); (c) Tracking with AUVs; (d) Tracking with AUVs(high mobility).

Fig.9.The performance comparisons of different tracking algorithms.

In Fig.10, 3-dimensional (3D) simulations are demonstrated to validate the usability of the proposed methods.The scenario and the localization and tracking performance are shown in Figs.10(a) and 10(b), respectively.In the simulation, to unify parameter settings, the number of used particles is still 200.Considering that scenarios with larger scales usually require more particles, the algorithms suffer from performance degradation due to insufficient number of particles,while the proposed CaCL and CaTT algorithms still outperform the alternative ones with clear advantages.Moreover, the robustness of the proposed methods to different levels of measurement noises is validated in Fig.10(c), where the distance and current measurement noises respectively with different standard deviations σrand σcare applied.To clearly illustrate the variation trends of the localization and tracking accuracy, the values of σrand σcare set larger than their empirical ones as stated in Section V-C and [6].From the results,measurement noises would inevitably lead to accuracy degradation of CaCL and CaTT.However, since the uncertainties are already considered in their design, the accuracy drops of the proposed methods are limited.The obtained localization and tracking accuracy is still better or at least comparable to the alternative methods (with smaller measurement noises)shown in Fig.9, even under such harsh measuring conditions,especially for current measurements.Thus, the adaptability of the proposed methods is verified.

To sum everything up, with the help of current information,the designed CaCL and CaTT algorithms provide better localization and tracking accuracy compared with alternative methods.Their adaptability to the harsh underwater environment is validated as well.

VII.CONCLUSIONS

This paper investigates the problem of multi-AUV cooperative localization and target tracking in anchor-free environments with the assistance of ambient current measurements and predicted current maps.Different from previous currentaided works that mainly deal with single-AUV localization problems, this work integrates current information with multi-AUV cooperation and improves the performance of both localization and tracking.Due to the real-time changing nature of the current, determining how to properly combine current information with localization and tracking and how to effectively alleviate the impact of current uncertainties are the keys to this research.

In this paper, we first integrated current information into the BP message-passing scheme, laying the theoretical foundation of the CaCL and CaTT algorithms designed through AUV cooperation.With the help of current, CaCL alleviates the impact of the accumulated errors in inertial measurements and effectively slows down the localization error growth of AUVs.In CaTT, current maps improve the prediction accuracy of the noncooperative target and accordingly result in better tracking accuracy.Moreover, considering the fact that the quality of current information may influence localization and tracking performance, the design of CaCL and CaTT mitigates the influence of current uncertainties by enlarging the particle coverage and prevents large accuracy drops even when current information is of poor quality.Through various simulations, the advantages of the proposed methods are validated by comparisons with alternative ones.Moreover, they are also evaluated with different qualities of current information, and their adaptability is verified.

Fig.10.3D validations.(a) 3D scenario; (b) Performance comparisons; (c) Influence of measurement noises.