基于GWR 模型的降雨事件前后武汉市东湖悬浮物浓度变化影响因子研究
甘文霞GAN Wen-xia;潘俊杰PAN Jun-jie;肖安娜XIAO An-na;杨如琴YANG Ru-qin
(①武汉工程大学土木工程与建筑学院,武汉 430205;②湖北交投智能检测股份有限公司,武汉 430050;③武汉市自然资源和规划信息中心,武汉 430014)
0 引言
武汉市作为百湖之市﹐其湖泊水环境直接影响着周边居民生活、城市生态与经济和谐发展。近年来,随着武汉市水环境综合治理规划实施,已基本实现“污水进管网、雨水入湖塘”目标,当前的城市内部湖泊水体污染主要来源为雨水径流[1],对降雨事件前后湖泊水质的影响因素及其特点进行分析具有重要的理论意义和实用价值。
学者们对水环境的影响因素研究已经做了很多工作,其中针对土地利用因素对雨水径流问题的影响研究较多[2,3],研究结果表明不同土地利用的差异会导致水质浓度有规律地差异分布。伴随着道路建设蓬勃发展,交通活动日趋频繁,由路面径流冲刷污染物进入受纳水体而产生污染也引起了人们重视[4,5]。但已有研究主要从水质的整体状态展开分析,将研究对象视为整体对其水质或污染源进行分析[6],但当水体面积较大时,其水质分布及其影响特点具有空间异质的特点,整体性的分析难以揭示影响因素作用的空间分布异质的特点,缺少对典型降雨事件带来的水质影响特征的精细分析。地理统计学中的地理加权回归(GWR,Geographic weighted regression)模型可探究不同自变量对因变量的影响强度和作用方向,并反应影响因素的空间异质特点[7],在不同行业中有着广泛应用,如生态指数、空气质量与碳排放指数等环境空间异质性分析。赵晶娅等[8]运用美国洛杉矶市的人口、路网、交通等数据,利用地理加权回归模型分析了多个影响因素对二氧化氮排放量的影响;陈晓辉[9]等利用地理加权回归,分析福州市不同建成区域环境对生态指数的影响,定量分析了生态指数的空间异质性;Wang[10]等使用GWR 模型,分析路网交通特征对城市空气质量的空间异质性影响;袁长伟[11]等基于我国各省运输业规模、技术以及结构三大影响因子,构建各省的碳排放量的地理加权回归模型,进而实现各地区碳减排压力指数的划分。
综合背景及现状,本文以武汉市东湖为例,采用地理加权回归方法,对降雨事件前后水体悬浮物浓度变化与不同影响因子之间的影响特征进行定量分析。武汉市东湖作为典型的大型城中湖,与城市和人群的地理交互关系密切,通过在东湖这一研究区域开展降雨事件分析研究,有助于揭示不同影响因素对水质影响的空间异质性,为区域水环境治理提供依据。
1 研究区域与数据
东湖位于湖北省武汉市城区东部,具体可细分为水果湖、郭郑湖、汤菱湖、庙湖、团湖、后湖、喻家湖等子湖[12],全湖面积在正常高水位19.78 米时为31.75 平方公里,是我国最大的城中湖泊(图1),是武汉市的重要水源地,和知名生态旅游风景区。西部水域与武昌区连接紧密,东、南、北三面为洪山区与青山区所围绕。
1.1 遥感影像与实测水质数据
本研究选择卫星多光谱遥感影像Sentinel-2 MSI 数据作为遥感水质反演影像数据源,分别选取降雨前后2021 年1 月19 日、2021 年1 月29 日两个时间的影像数据进行了悬浮物浓度反演,东湖悬浮物反演模型使用卢东烁[13]构建的东湖水质参数波段组合反演模型。
1.2 影响因子数据
从研究区域的社会、经济、基础设施等实际状况出发,结合已有研究中对雨水径流及其影响因素的探究,以及降雨通过雨水冲刷进而影响湖泊水质的过程分析,构建了城市湖泊水质初选影响因子集合如表1 所示,其数据来源包括网络公开数据及解译数据[14],研究中还将采用因子筛选方法进一步挑选主要影响因子。

表1 城市湖泊水质初选影响因子
2 研究方法
本研究中首先统计了东湖悬浮物浓度的空间自相关性,之后通过相关性分析和共线性检验,并结合事件特点,进行了影响因子的筛选,最后对悬浮物浓度与2.2 中不同因子进行了地理加权回归建模,基于建模结果分析不同因素对降雨前后悬浮物浓度变化的影响程度和空间特征,具体方法分别如下。
2.1 空间自相关分析
空间自相关性可以反映空间变量在各个区域上的相互依赖程度[15]。本文采用在地理统计研究中经典的莫兰指数探究水质的全局空间自相关性,作为空间异质性判定依据[16],其计算公式为[17]:
式中:I 为自相关度量指标;N 为研究区域内的悬浮物浓度数据点位数量;z¯为悬浮物浓度的平均值;zi、zj分别为悬浮物浓度数据的空间位置,wij为zi、zj的距离。
2.2 地理加权回归模型
地理加权回归(Geographically Weighted Regression)模型,将数据的空间位置嵌入到回归参数中,建模得到不同地理位置各自变量与因变量间不同的空间关系[18],模型如公式(2)所示:
在本文研究中,式中(ui,vi)为第i 个悬浮物浓度反演数据的坐标(经纬度投影坐标,单位为m),β0(ui,vi)为第i个悬浮物浓度反演数据的常数项,βk(ui,vi)为第i 个悬浮物浓度反演数据内第k 个自变量的估计系数,p 表示显著影响水质分布的自变量个数,εi为第i 个悬浮物浓度反演数据的随机误差。
2.3 相关性分析及共线性检验
地理加权回归模型求解时,如果因子之间存在局部多重共线性,地理加权回归模型的结果将变得不稳定,因此需对备选影响因子间的相关性分析与多重共线性检验,以保证解释变量的独立性,提高模型准确度。本文采用容忍度(Tolerance)和方差膨胀系数(variance inflation factor,VIF)指标来共同度量影响因子间的多重共线性[19],方差膨胀系数为容忍度的倒数,其计算公式为:
式中Ri表示该影响因子与其他影响因子之间的相关系数,i 为不同因子的编号。
3 结果和讨论
3.1 典型降雨事件前后路域水质路域水质空间自相关分析
图2 分别展示了降雨前后悬浮物浓度变化量空间自相关分析的局部莫兰指数散点图以及LISA 聚类地图。降雨前后悬浮物浓度差异的莫兰指数为0.482,表明其在空间上呈显著的正空间自相关(P<0.01),即其在空间上趋于集聚。从LISA 聚类图可发现其空间聚类特征明显,东湖北部和东部呈现出高-高聚类,西部则呈现出低-低聚类,具有显著的空间异质性。

图2 降雨前后悬浮物变化空间自相关分析图
3.2 地理加权回归模型因子相关性分析及共线性检验
表1 所列初选影响因子之间的相关系数如表2 所示,从表2 可以发现,在选定的八个因子中,X4(道路面积)、X5(道路宽度)、X6(道路长度)以及X8(车辆速度)具有显著相关性,即这几种初选影响因子间存在紧密联系,特别是道路宽度与道路速度,两者的相关系数为0.992,说明车道宽度与车速和道路通行能力之间具有高相关性。

表2 初选影响因子相关系数
表3 为初选影响因子共线性诊断,八个初选因子中,建筑面积(BR)和道路面积(RR)初选因子的VIF 小于10,分别为8.946 与5.005,说明这两种因子与其他初选因子不存在多重共线性。森林面积(FR)、绿地面积(GR)、道路长度(RL)和交叉口数(RC)这四种初选因子的VIF 大于10 小于100,这表明这四种因子与其他初选因子存在较强的多重共线性,需结合相关性分析结果判断其是否保留。

表3 初选影响因子共线性诊断
综合以上初选影响因子相关系数及多重共线性检验结果,本研就选择保留对于VIF 较大但相关性小于0.7 的影响因子,最终确定选取了建筑面积(BR)、森林面积(FR)、绿地面积(GR)、道路面积(RR)以及交叉口数(RC)这五个因子作为地理加权回归的影响因子。
3.3 地理加权回归模型结果分析
地理加权回归R2以及影响因子系数分布图如图3 所示,总模型拟合精度整体上呈现由外向内扩散性递减的圈层关系,即湖岸拟合效果好,湖心拟合效果差。主要原因是湖岸水质受影响因子影响程度高,湖心水体由于水的流动性,其水质分布较为均匀,导致地理加权回归模型无显著关系。
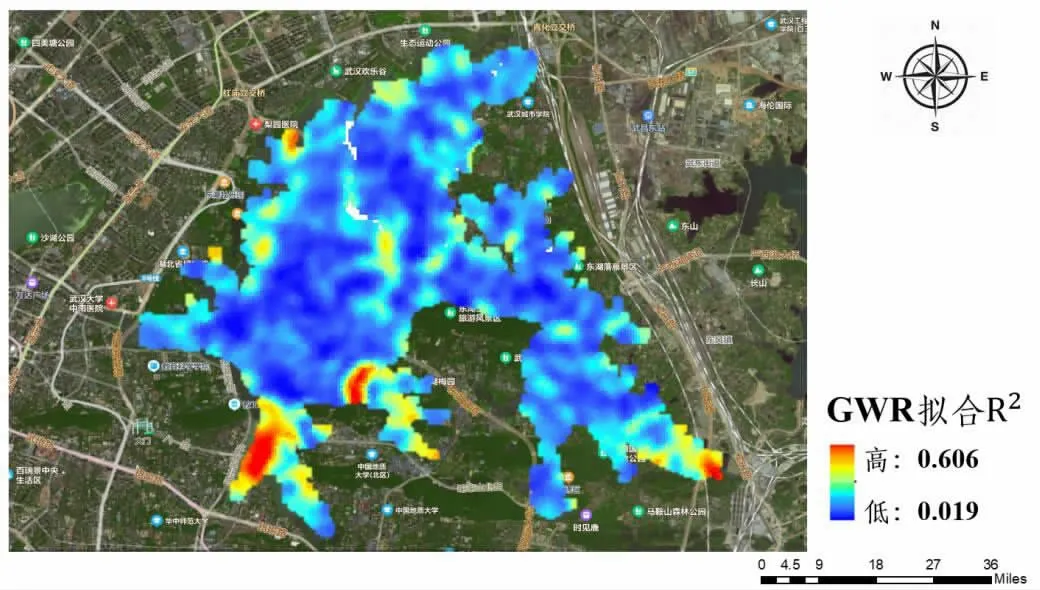
图3 地理加权回归R2 分布图
地理加权回归影响因子系数分布图如图4 所示,总体来看,各影响因子的回归系数在地理空间上存在明显的非平稳性,各影响因子对于水质的影响能力和影响效应有所不同,进一步证明了影响因素的空间异质性。

图4 地理加权回归自变量系数分布图
①道路面积、交叉口数与悬浮物浓度在水体边缘区域内总体呈正相关,即道路面积越大、道路交叉口数量越多,该区域的悬浮物浓度越高。主要原因是道路面积越大,车流量越大,道路残留污染物越多。
②建筑物面积与悬浮物浓度在水体边缘区域内总体呈正相关,即建筑物占地面积越大,该区域的悬浮物浓度越高。主要原因是建筑物高密度地区势必会产生较多的屋面雨水径流排放,进而导致水体固态悬浮物污染加剧。
③森林、绿地面积与悬浮物浓度在水体边缘区域内均呈负相关。主要原因是森林与绿地对雨水具有截留、吸收以及净化作用,减少了雨水径流排放对水体带来的污染。呈正相关部分区域周围为建筑物、道路密集区,路面硬化面积大,树木、绿地对雨水径流的减少作用不明显。
4 结论
本文以降雨事件前后,城市湖泊悬浮物变化为研究对象,采用地理加权回归方法对其影响因子进行分析。结果表明:
①考虑空间异质性的GWR 模型对降雨前后悬浮物浓度变化与影响因子间具有较好的拟合度。
②各影响因子系数在地理空间上存在明显的非平稳性,进一步证明了影响因素的空间异质性。
③建筑物面积与悬浮物浓度在水体边缘区域内总体呈正相关,即建筑物占地面积越大,该区域的悬浮物浓度越高;森林、绿地面积与悬浮物浓度在水体边缘区域内均呈负相关;道路交叉口数、道路面积与悬浮物浓度在水体边缘区域内呈正相关。
在本研究的实验过程中仍存在一些不足之处,对影响因子的选取可加以扩展,如从自然、社会、建成环境、交通系统等方面出发,构建城市湖泊水质影响指标体系。尽可能全面衡量其影响因素,使得所建模型精度更高,拟合效果更理想,研究更加科学、准确。
——以多重共线性内容为例

