基于虚拟同步型风力发电机组的风电场动态聚合模型研究
季一润,槐 青,袁 茜,宋 鹏
(国网冀北电力有限公司电力科学研究院,北京 100045)
为了有效应对日益严重的能源及环境问题,风力发电在世界各国迅速发展。2021年我国风力发电量6 526×108kW·h,同比增长40.5%,全年新增风电装机4 747×104kW,全国风电平均利用率96.9%[1]。随着大量并网风场对电力系统稳定性的影响逐渐增大,风场动态聚合模型越来越受到专家学者的关注[2-3]。由于风场通常由大量风机并联汇流而成,各台机组间的空间分布性和控制差异性较明显。为了避免系统的阶数及非线性度过高,研究并网风场对电力系统的影响时需要对并联机组进行等值建模[4-5]。
目前常用的聚合等值方法主要分为容量加权法、接口拟合法和同调等值法等[6-7]。容量加权法依据参数一致原则,以每台机组容量为权重,将同一型号及控制模态的机组直接等值为一台风力机组。这种方法在风速不均、地理分布广、风机型号较多的风场中不能有效降低系统阶数[8-9]。而接口拟合法为了最大程度降阶,将风场并网接入点PCC(point of common coupling)特性等效为一台发电机组,将聚合问题转化为电机的参数求取及最优化问题[10-12],但一套优化参数通常难以满足风场复杂工况的要求。同调等值法依据同步发电机聚合原则,将具有相似的机端电压、定子频率变化方式的机组加以聚类,但风力机组种类各异,实际频率、电压动态特性由各自变换器控制参数决定,当前基于电网电压矢量定向的最大功率点跟踪MPPT(maximum power point tracking)控制使得各机组间缺乏统一的动态响应规律[13-15]。传统矢量控制下各机组动态差异明显,风场内风速及风向变化多样,通过聚类、分群的方法很难将风场聚合为一台机组并表征不同工况下的并网特征,为高风能渗透率下的电网稳定性分析提供有效模型。
基于上述分析,本文提出一种基于虚拟同步型风机的风场动态聚合方法,使得各风机并网频率和电压动态响应特性在虚拟惯量、阻尼系数的约束下具备一致性。近年来虚拟同步机VSG(virtual synchronous generator)思想逐步得到重视[16-18],其中VSG型风机由于具备模拟同步发电机外特性的能力[19-20],为风场依据传统电力系统进行动态聚合提供了控制基础。同时,聚合后的风场模型阶数及物理特征与传统同步电机相接近,增强了电力电子型电源与以同步机为主导的电力系统的融合性。
1 虚拟同步型风机的基本控制
VSG型风机需构建发电机本体、励磁器及调速器模型,本文采用的本体模型为
式中:J为转子惯量;α为转子角加速度;Tm为机械转矩;Te为电磁转矩;K为阻尼系数;ω为转子转速;u=[uaubuc]T为定子相电压;i=[iaibic]T为定子相电流;eo为反电动势;Rs和Ls分别为定子电阻及电感。
调速器和励磁器模型为
式中:Dp为有功下垂系数;Dq为无功下垂系数;f、fn和Δf分别为当前频率、额定频率和频率偏差;Pe、Pn和ΔP分别为当前有功功率、额定有功功率和有功功率偏差;uref、un和Δu分别为当前电压、额定电压和电压偏差;Q、Qn和ΔQ分别为当前无功功率、额定无功功率和无功功率偏差;为标幺化后的有功下垂系数和无功下垂系数。
目前主流风机为双馈异步型DFIG(doubly-fed induction generator)和全功率变换型PMSG(permanent magnetic synchronous generator)。为使不同类风机具备动态一致性,风力机组的VSG控制也应具备通用性。
1.1 传统风机的动态特性
传统DFIG通过其转子侧变流器实现并网功率的解耦控制,并通过锁相环PLL(phase locked loop)将系统dq坐标系按电网电压矢量定向,忽略定子电阻后可得输出有功功率Ps及无功功率Qs分别为
式中:Lm为互感;us为定子电压;ψs为定子磁链;ird和irq为转子d、q轴电流。传统并网策略基于电网电压定向的矢量控制,动态特性受PLL及dq轴电流调节器参数影响较大,加之各机组运行工况各异,各自变频器内部参数复杂,缺乏明确统一的物理含义,各风机之间无法形成有效的参数统一。所以当前基于传统矢量控制的风力发电机组之间仅能对稳态输出功率进行等值聚合,而在系统扰动过程中的动态特性缺乏聚合基础。
1.2 虚拟同步型风机的动态特性
采用VSG控制的风机其稳态依然满足MPPT,机电动态特性主要取决于变流器中虚拟惯量、阻尼系数等控制参数。考虑风速变化过程中风机依据MPPT寻找最佳转速,转子惯量使其动态过程慢于VSG模型动态时间常数,不同VSG参数机组在风速变化下的动态差异小,而在电网扰动下的动态差异显著。分别以1.5 MW的PMSG型风机及DFIG型风机为例,仿真2 s时电网频率由50 Hz跌至49.75 Hz过程中的输出动态特征,风机参数如表1和表2所示,仿真结果如图1所示,各机组在频率扰动下,输出功率支撑最大值均接近0.88 MW,调节时间为2 s,动态差异具备较好的规律性。
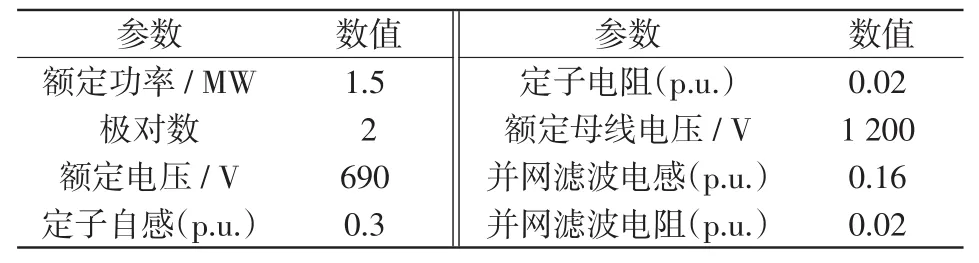
表1 PMSG风机参数Tab.1 Parameters of PMSG wind turbine
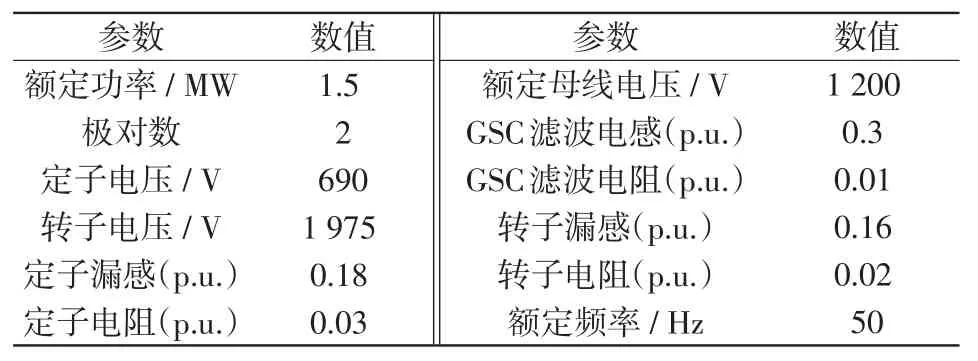
表2 DFIG风机参数Tab.2 Parameters of DFIG wind turbine
从图1可看出,虽然电机自身的阻感大小、内部损耗及并网连接方式不同会造成不同机组的电磁暂态过程以及稳态功率的微小差异,但机电动态过程依然受VSG方程约束,具备与传统同步机相似的同步转子摇摆特征和动态可聚合性。
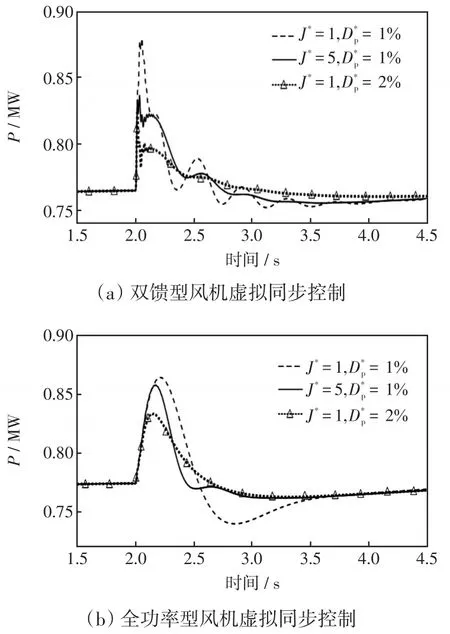
图1 虚拟同步型风机并网功率外特性Fig.1 Power performance of VSG wind turbines
2 虚拟同步型风场动态聚合模型
2.1 机组自同步机理
在由大量传统同步发电机构成的电力系统中,多台机组即使在复杂的电网络下,在满足聚合条件后可具备频率同步特性。受传统同步发电机聚合过程的启发,可进一步利用虚拟同步型风机并网接口的动态一致性。首先通过二阶非均匀Kuramoto(KM)模型揭示复杂电网络下传统同步发电机组之间的自同步机理。
设复杂电力网络是由N台传统同步发电机组构成,考虑到风场内部汇流线上一般不会挂接额外负载,所以该网络中仅需列写发电机方程,即
(1)电网络中的等效阻抗时间常数远小于发电机转子摇摆时间常数;
(2)发电机电压调节时间常数远小于发电机转子摇摆时间常数;
(3)发电机转子位置角与电动势矢量重合。
在自然界中,同步问题涵盖了物理、化学、生物等各个领域。通过KM模型进行相关数学证明,能较好地解释自同步问题的共性。典型的二阶非均匀KM模型为
式中,mi、ki、θi、Ωi、aij分别对应振子i的惯性常数、阻尼系数、相位、自然频率以及振子i与振子j的耦合系数。而式(4)可进一步改进为KM模型下的表达形式。传统电力系统中同步发电机的聚合依然需要满足一定条件,若使用二阶非均匀KM模型的频率同步定理判定该系统稳定性,通过已有判据可知,上述KM模型还需要满足以下3个条件:
(2)系统基础图的结构参数Lˉ>0,其为系统频率同步的必要条件;
(3)各机组在标幺值系统下具备恒定的阻尼惯量比。
若实际风电场中的风机均采用VSG控制,受变流器中虚拟同步轴控制模块的约束,各台机组并网处的内电势与同步发电机内电势的机电动态特性一致,可以用同步发电机的转子方程描述,其中和分别对应虚拟同步型风机中的可调参数J及K;对应各风机的MPPT功率指令,对应各台机组间的功率传导矩阵。可以看出,采用VSG控制后风场内各风机的并网机电动态特性能够体现为传统同步电机的输出外特性,且满足应用基于二阶非均匀KM模型的机组自同步机理的必要条件。
2.2 小信号模型
采用VSG控制的PMSG型和DFIG型风机的小信号模型具备相似性,其小信号模型如图2所示。
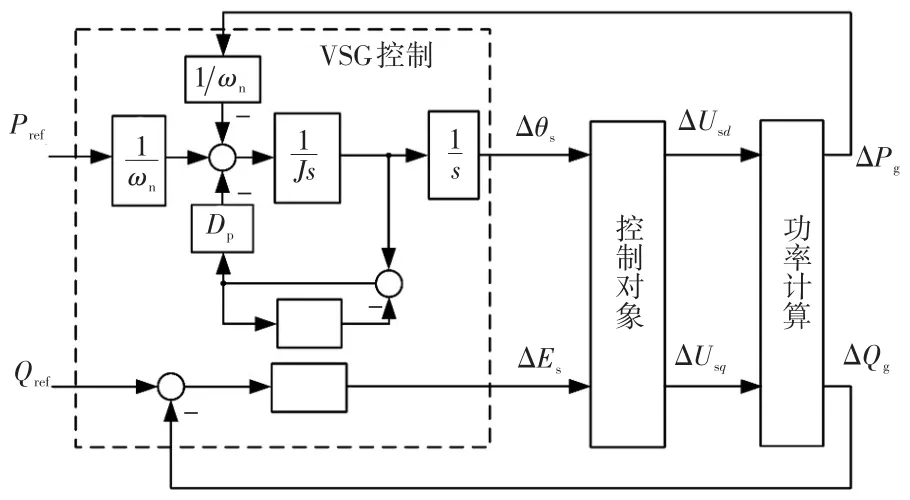
图2 虚拟同步型风机的小信号模型Fig.2 Small signal model of VSG wind turbines
设有功功率参考值及无功功率参考值分别为Pref和Qref,电网电压d、q轴分量为Ugd和Ugq,发电机端线路电抗为Xg,电网同步转速ωn,Δθs为同步轴相位扰动,ΔEs为内电势幅值扰动,ΔUgd和ΔUgq为电网电压d、q轴扰动。根据dq轴计算公式,假设端电压ΔUsd、ΔUsq为扰动项,则输出功率的传递函数为
由于两类风机并网接口的机电动态响应特征均受VSG模型约束,在机电时间尺度上的小信号模型相近,由VSG本体式(1)决定。并且,机电动态约束方程与上述基于二阶KM模型的方程相近,基于VSG控制的风电机组也具备自同步特征,可进行机电时间常数上的动态聚合。以当前风机的MPPT指令作为功率基值选取参数,电力系统对频率及电压一次调节下垂系数均有明确规定。同时,控制系统中虚拟惯量可以通过有功调节时间常数τp及下垂系数依据公式进行定义。虽然风速快速变化可以达到Hz级,但波动风速通过风轮惯量滤波后再生成MPPT指令输出至VSG模型作为功率参考值Pref,合理设置τp可保证VSG控制内环在频率支撑过程中外环参考功率相对稳定。
2.3 动态聚合方法
由基于KM模型的机组自同步理论可知,通过VSG控制与参数整定后,各台风机动态特征与传统同步发电机相似,不同风电机组间亦满足自同步机理。风场动态聚合的具体目标即是将各台风机VSG模型中的机电动态方程以及机端电压稳态方程用统一的聚合方程组表征,同时该聚合方程组中各系数可由各台风机的对应参数求取。从而由n台机组并联汇流成的混合型风场可聚合成为一台具备同步发电机动态外特性的风力机组,如图3所示。
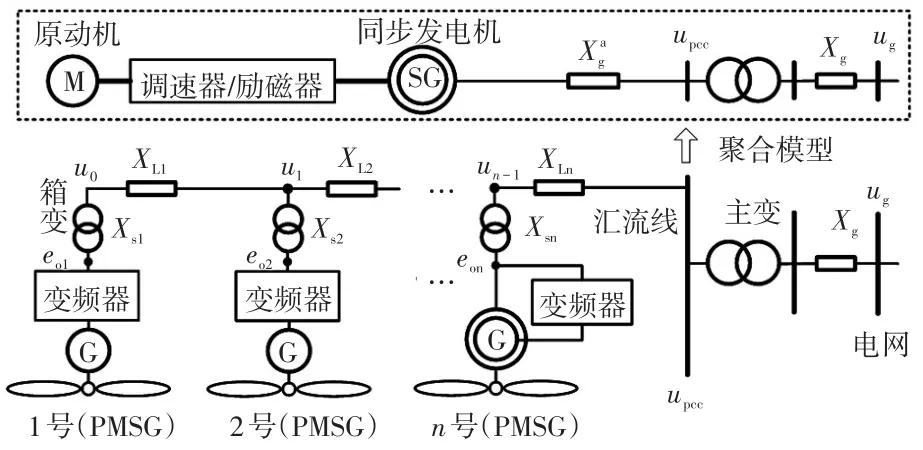
图3 风场架构及其聚合模型Fig.3 Structure of wind farm and its aggregation model
图3中:机端等效阻抗Xs为机组虚拟阻抗Xv、实际输出阻抗Xo及箱变等效阻抗XT之和,其中Xv为柔性参数,可根据聚合需求整定;XLk为k号机组汇流线阻抗;eok为k号机组的反电动势;ik为k号机组输出电流;Pk为第k台机组功率;k=1,2,…,n;upcc为风场并网点电压;ug为电网电压;为聚合模型等效同步电抗。首先进行风机机端电压稳态方程的聚合,若风场中各风机采用基本的单位功率因数输出方式运行,各风机对应汇流点电压幅值各异,此时以位于汇流线末梢的2台机组为例,在u1处的端电压表达式为
式中:P1、P2为等电位点聚合将各机组当前风速下的MPPT功率,为了便于在等电位点聚合,将P1、P2作为方程的权重;u1可分别由1号、2号机组的输出电压方程表示。并联机组的阻抗匹配程度决定了其端电压的动态可聚合性。令P1(Xs1+XL1)=P2Xs2,可得聚合电压方程为
在第h-1个汇流点的电压聚合条件为
式中:Ph为第h台机组功率,2≤h≤n;Pj为第j台机组功率,j=1,2,…,h-1;Xsh为第h台机组机端等效电抗。对于包含n台机组的系统,可得任一汇流点电压方程为
其使得各机组输出功率在等效输出阻抗及汇流线上产生的总电压降可以反映风场并网功率在上的电压降。在动态功率标幺系统下,各台虚拟同步型控制的机组频率特征可由其VSG模型中的机电方程表示为
各机组根据MPPT功率标幺VSG参数,设定相同的标幺化虚拟惯量及阻尼系数K*,在标幺化输出机械转矩及标幺化电磁转矩的作用下,各台机组角加速度以及相同时间内的频率变化率相等。设聚合后角加速度和频率变化率分别为αa和Δωa,由于角速度及其变化率在相同时间内的动态过程中满足
式(12)中的各机电方程可聚合。
综上,采用VSG控制的各台风机的机电动态方程、端电压方程和同步电抗可分别表示为
式中:αa和Δωa分别为机组反电动势相角和机组对应的汇流点电压相角;为聚合模型并网点电压;为同步电抗。机电动态方程与稳态电磁方程的关系则通过各机组的转矩表达式相关联,即
式中,δh和δh-1为第h台及h-1台机组VSG转子相位角。
动态过程中,各机组的频率变化率接近,由归一化后的虚拟惯量、阻尼等系数K*决定,而端电压特性由归一化的励磁调节参数决定,同时,加权系数Ph由各机组当前MPPT功率表示,由于Ph根据实际转子转速获取,转子转速受风轮转子的惯量约束变化较慢,且为保证VSG系统稳定所设置的虚拟惯量小于实际风轮惯量,所以该动态聚合方法满足频率、电压动态特征的等效性。
在该聚合模型基础上还需对分布式风轮机做等值,并将其作为同步发电机组的原动机。由于同一功率等级的风轮机转子惯量时间常数较接近,且远大于虚拟同步电机控制的有功-频率闭环时间常数,所以可用等效惯量时间常数Hw表征转子惯量Jw为
根据系统额定容量Sn、额定频率fn和转子极对数p可以确定等效惯量。风轮机在系统中主要决定MPPT的闭环时间,包含风速扰动过程中的功率跟随以及网侧扰动后MPPT恢复过程。最后,用等效风速表征风场当前吸收的风能,并作为等效风轮机的输入变量。
3 仿真算例
首先通过含电磁暂态和机电动态的精细化风机模型验证所提出的聚合方法的有效性,再进一步考虑实际风速波动以及电网扰动的工况下,通过风机的机电动态模型验证所提出方法在大型风场中的可行性。
以风机的PWM平均模型为基础构成小型汇流网络,验证上述聚合方法对2台风电机组的并网功率的动态聚合效果。PWM平均模型包含完整的变流器控制闭环、发电机本体和风轮机的模型,与实际系统较为接近,但也使得其阶数和非线性度大幅提高,较难应用于实际的大型风场中。设2台1.5 MW风机的实际输出阻抗均为0.202 mH,即0.2 p.u.,XL1、XL2汇流线阻抗均为22.5 μH,计算风场并网总功率,并将其作为功率对比仿真结果中的风场实际模型的功率曲线。其中1号为PMSG型风机,2号为DFIG型风机,二者均采用VSG模型,设虚拟惯量时间常数为0.6 s,标幺值有功下垂系数为100,设DFIG型风机的转子惯量时间常数与PMSG型风机的相同,均为5 s。在相同工况下用一台额定功率为3 MW的实际同步发电机来表征上述2台采用PWM平均模型的虚拟同步型风电机组,该聚合模型中的同步机发电机组参数如表3所示。
表3 动态聚合同步发电机参数Tab.3 Parameters of synchronous generator in dynamic aggregation model
考虑到大电网是由大型同步机并联构成,为了反映真实电网的频率变化规律,用一台30 MW的同步发电机组代替无穷大电网模型,初始负载30 MW。仿真中在2 s时1号机组和2号机组的对应风速分别从9.0 m/s和8.8 m/s上升至9.5 m/s和9.2 m/s,由于该算例中风速的变化规律较为简单,可计算出额定功率为3 MW、风轮等效惯量时间常数为5 s的风场聚合模型中的原动机对应等效风速从8.93 m/s上升至9.38 m/s。通过12 s时负载突增5%仿真电网扰动时的聚合模型动态响应,分别观测各机组及风场并网功率和系统频率,对比结果如图4所示。
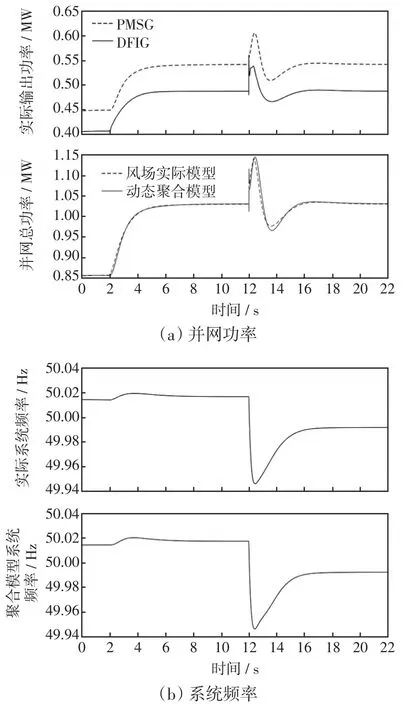
图4 风场实际模型与动态聚合模型的对比结果Fig.4 Comparison resultsbetween actual wind farm model and dynamic aggregation model
从图4中可以看出,随着风速的提升,实际模型的系统频率在2 s后出现小幅升高,由于该过程中风轮机转子转速上升较慢,系统频率变化率较小;12 s时的5%负载突增使得表征电网的30 MW同步发电机电磁功率突增,系统频率在同步机转子惯量以及VSG虚拟惯量的约束下大幅跌落,并随着风机恢复MPPT而进入新的稳定工作点,聚合模型对系统的频率支撑效果与实际模型保持一致。
实际风场中风速波动具有随机性,算例2通过SCADA系统传递的各机组MPPT指令值代替聚合模型中原动机的输出机械功率,并以VSG模型的输出内电势作为受控电压源代替风机的PWM模型,以完整33台风机的实际风场为例验证本文提出的聚合方法在大型风电场中应用的可行性。风场汇流线参数如表4~表6所示,聚合模型中的同步发电机参数的标幺值与表3一致,仅额定功率提升至49.5 MW,大电网用一台额定容量为200 MW的传统同步发电机表示,初始负载200 MW。3条汇流线对应的风速如图5所示。
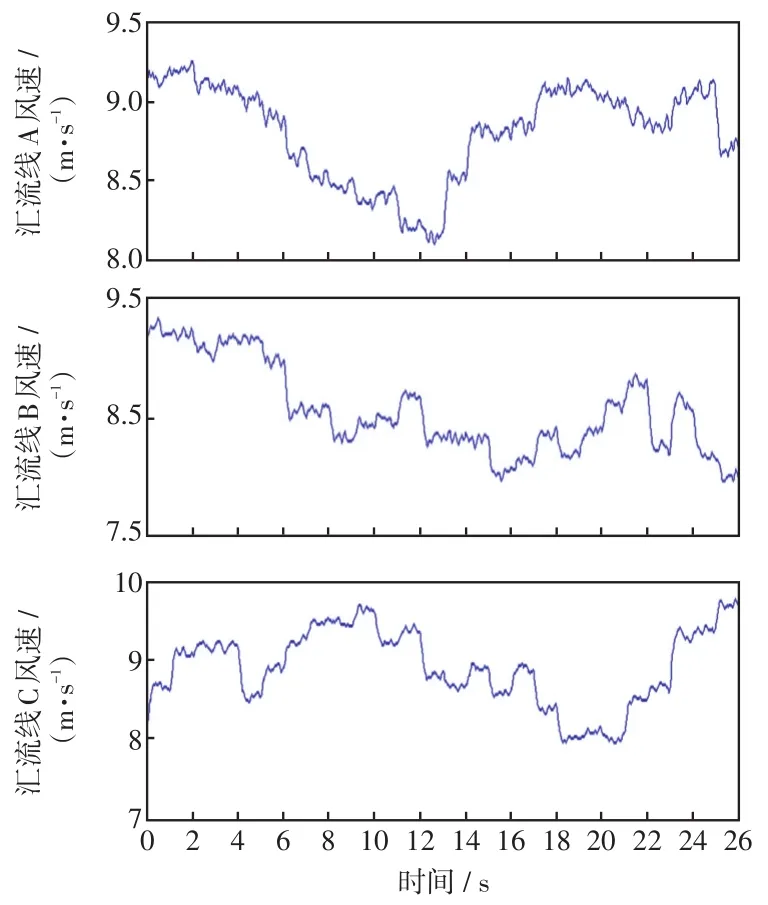
图5 汇流线对应的短期风速曲线Fig.5 Short-term wind speed curves of feeder lines
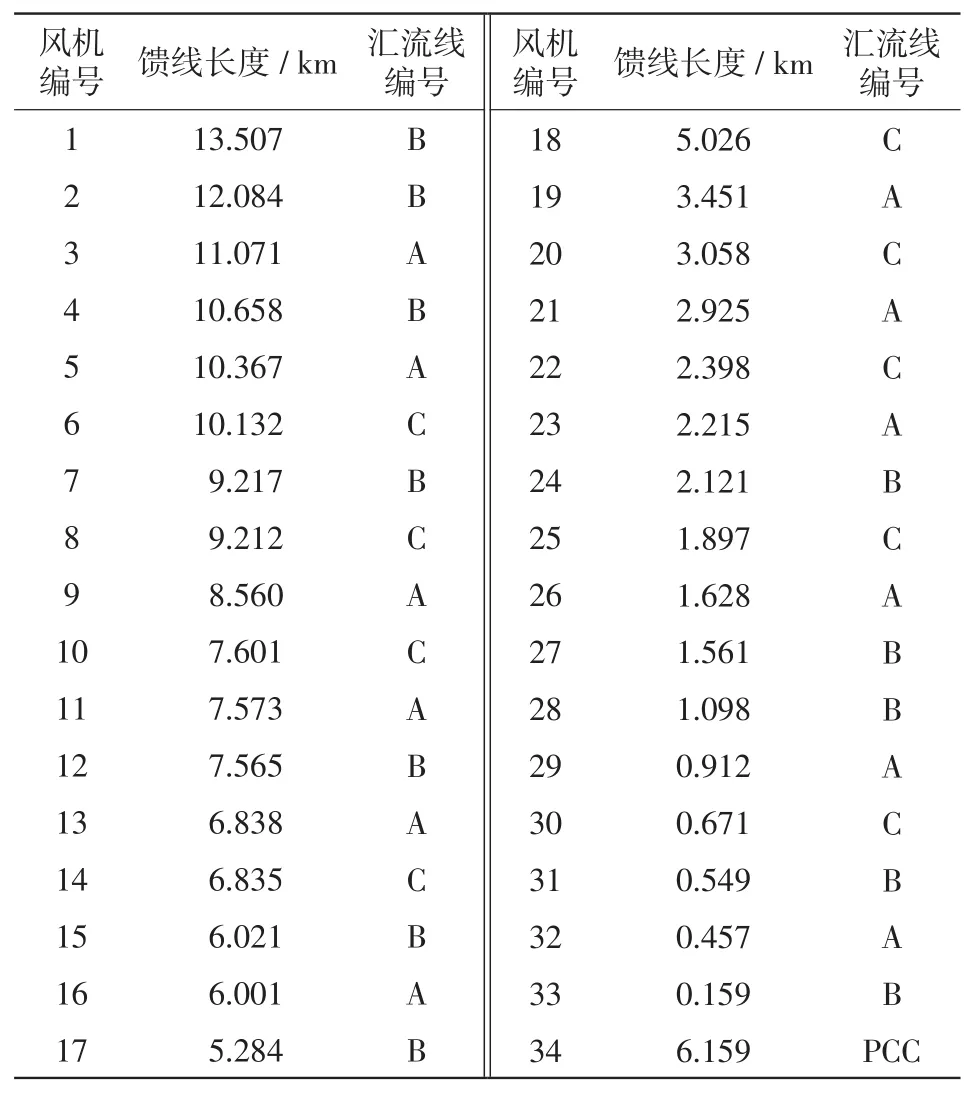
表4 风场馈电线路架构信息Tab.4 Construction information about feeder lines in wind farm
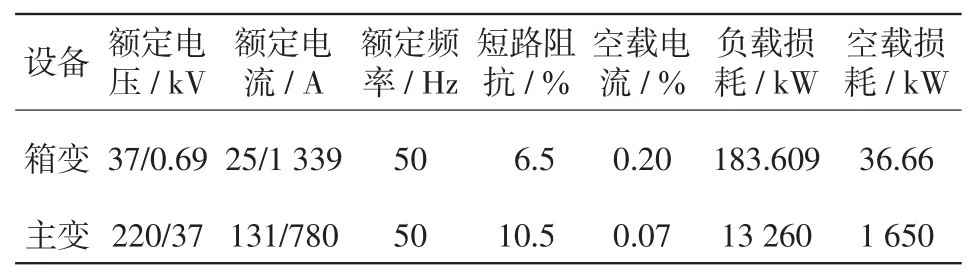
表5 风场变压器参数Tab.5 Parameters of transformers in wind farm

表6 风场线路参数Tab.6 Parameters of feeder lines in wind farm
进一步将SCADA系统上传的3条汇流线的MPPT数据相叠加,作为风场动态聚合模型中同步发电机的机械驱动功率。在聚合模型的仿真中同样通过2 s时的5%负载突增以及12 s时的负载恢复过程,验证聚合模型的并网动态特性。将该工况下的聚合模型并网功率波形与实际风场模型中3条汇流线在PCC点的并网总功率做对比,结果如图6(a)所示,系统频率如图6(b)所示。
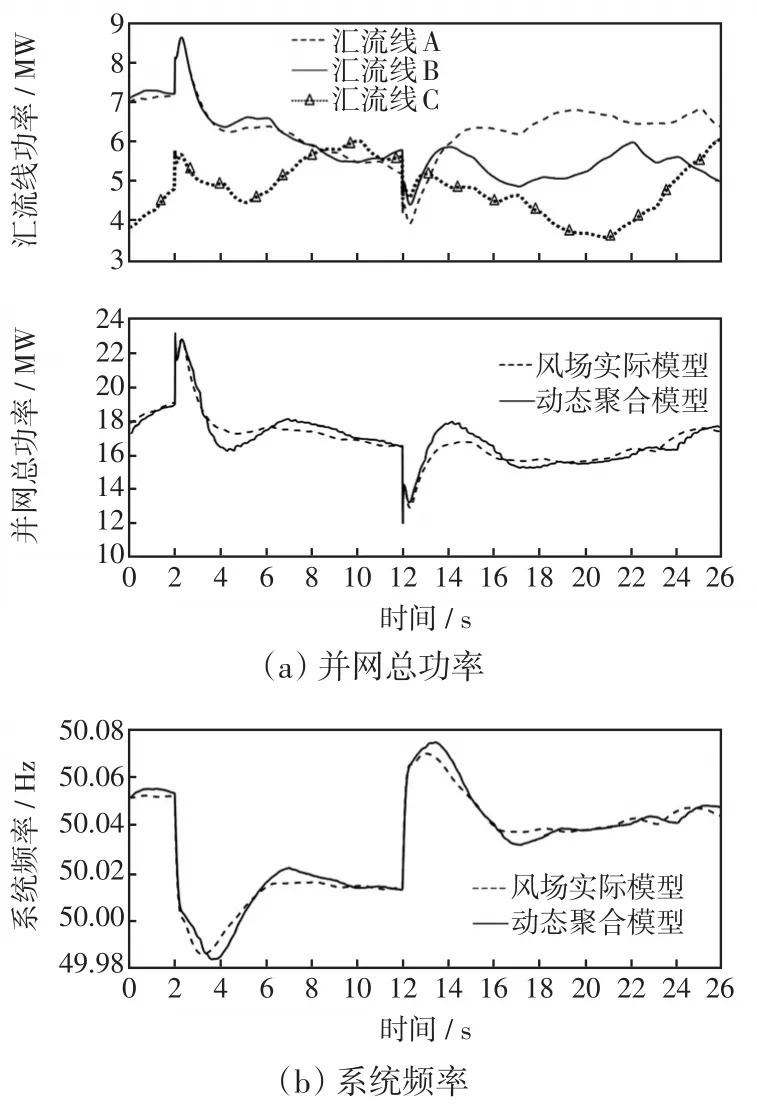
图6 风场实际模型与动态聚合模型的对比Fig.6 Comparison between actual wind farm model and dynamic aggregation model
仿真2 s时网侧负载突增5%,由于汇流线A和B的扰动前稳态输出总功率接近,2条汇流线承担的动态支撑功率也相似,而汇流线C由于扰动前的稳态功率较小,根据稳态功率均分的动态支撑功率也较少,但3条汇流线的功率动态调节时间基本一致;当12 s系统恢复额定负载时,3条汇流线的功率动态特性依然保持较高的一致性。同时,从图6(a)的并网总功率对比曲线可以看出,聚合模型与实际模型的输出功率存在小于10%的偏差,但仿真全过程中的最大功率跟踪趋于依然保持一致。图6(b)中的系统频率变化过程可以体现风场对大电网惯量的贡献作用,在负载突增过程中实际模型与聚合模型的系统频率最低点均为49.98 Hz,而在负载恢复过程中两者的频率最高点均达到50.07 Hz,且频率调节时间一致。
在算例2中,虽然聚合模型的输入机械功率需要依赖SCADA系统上传MPPT数据,但仅需将其简单累加便可作为聚合模型中同步发电机的驱动功率,且各机组的机电动态一致性由各自的VSG控制保证。相比于需在上位机中对相关数据进行最优求解及接口拟合的聚合方法,该模型可更加快速、准确地获得风场输出功率的机电动态特性。同时可以看出,即使在算例2中计及了一定的通讯延时,但由于MPPT指令本身也已经通过转子惯量滤波,其变化率小于风速的波动频率,所以通讯延时对聚合模型输出功率的准确性影响得到进一步减小,并且由于聚合模型的机电动态方程与虚拟同步轴方程相同,两套模型在电网扰动过程中的动态频率响应机制相似,所以该聚合方法适用于大规模风电场的聚合建模中。
4 结语
本文首先通过二阶非均匀KM模型阐述了复杂电网络中多机自同步的必要条件,该理论广泛适用于当前以同步发电机为主导的电力系统稳定性分析中。考虑到VSG控制模型与同步发电机的机电动态方程一致,上述自同步理论的相关论据也可以作为虚拟同步型风机动态聚合的理论支撑;继而提出了基于虚拟同步型风机的风电场动态聚合方法,推导了多台风电机组并联汇流后的机端电压方程、虚拟同步轴方程及其数学聚合公式,同时给出了各台风机应设置的虚拟惯量、阻尼系数以及虚拟同步阻抗的求解方法;最后,通过基于PWM平均模型的DFIG型风机与PMSG型风机的并联仿真,验证了上述聚合方法的有效性;进一步在考虑实际风速波动以及电网扰动的工况下,通过33台风机的机电动态模型验证了所提出的聚合方法应用于实际风场中的可行性。
由于不同类型机组的并网方式差异及风场实际网络架构的阻抗差异,电磁暂态过程中的风场可聚合性及聚合机制有待进一步研究。

