基于改进鲸鱼优化算法的光伏发电系统MPPT控制研究

陈 斌，王俊江，赵明胤，赵芳正

（1.山东理工大学电气与电子工程学院，淄博 255049；2.山东科汇电力自动化股份有限公司，淄博 255087）

随着全国“碳达峰、碳中和”目标的提出，光伏等新能源发电方式备受人们的青睐，光伏电站规模不断扩大[1-2]。然而，在实际应用中，受外界环境及天气因素的影响会导致局部阴影情况的出现，使光伏阵列呈现多峰值性，从而降低光伏阵列的发电效率[3-6]。所以避免陷入局部极值，并提升全局最大功率点跟踪MPPT（maximum power point tracking）能力已成为一个至关重要的研究课题。

文献[7]提出一种基于自适应的扰动观察法，能加快迭代速度并提升优化精度，但不宜在遮阴状态下使用；文献[8-9]提出一种新型鲸鱼优化算法WOA（whale optimization algorithm），通过引入非线性收敛因子来提升寻优精度；文献[10]提出一种免疫萤火虫算法，采用建立疫苗库的方式来提高迭代速度，迭代速度较快，但难以精确有效地实现全局MPPT；文献[11]提出一种改进粒子群优化PSO（particle swarm optimization）算法的MPPT控制方法，可以减少振荡，提高系统稳定性，但无法避免PSO算法易较早收敛于局部最优解的弊端；文献[12]对粒子群算法进行了改进，可以提高系统的稳定性，但此算法易较早收敛于局部最优解；文献[13]将随机惯性权重引入到粒子群算法中，并将其应用于阴影遮蔽情况下MPPT的研究，可以提高跟踪的效率并减少系统的振荡；文献[14]提出一种粒子群-布谷鸟混合算法，可以使系统及时跳出局部最优解，并提高搜索的精度，但控制相对复杂，成本较高；文献[15]提出一种改进的粒子群算法，通过引入非线性收敛因子提升寻优的速度及精度，但未对系统的振荡进行抑制；文献[16]提出一种混合混沌粒子群算法，并将其应用于MPPT控制策略中，可以改善算法后期振荡问题，提高系统稳定性。

目前，传统MPPT算法在光伏发电系统的多峰值MPPT应用中存在收敛速度慢、效率低下、容易陷入局部功率极值等弊端。智能算法在多峰值寻优的过程中也存在跟踪速度慢，功率输出不稳定等问题。因此，本文在以上研究的基础上，提出了一种改进型鲸鱼算法IWOA（improved whale optimization algorithm），并用其解决局部遮阴等复杂工况下的光伏多峰跟踪问题。采用Tent混沌映射增加种群的多样性；通过引入非线性收敛因子使光伏发电系统的最大功率点跟踪能力得到提升；通过引入非线性时变的自适应权重使系统及时跳出局部最优解，提高全局的搜索精度。最后，通过仿真对比验证了改进型鲸鱼优化算法的优越性和准确性。

1 光伏阵列的输出特性

光伏阵列由光伏组件串并联而成。在太阳光照射的过程中，光伏阵列会受到落叶、遮挡物及云层等的影响，从而导致局部阴影情况的出现。

通过Matlab/Simulink软件搭建一个3×1的光伏阵列。设定光伏电池的温度均为25°C。为更有效地模拟局部阴影对光伏阵列的影响，将光伏电池接收不同情况的光照。各种光照情况的仿真参数如表1所示。光照仿真效果如图1所示。

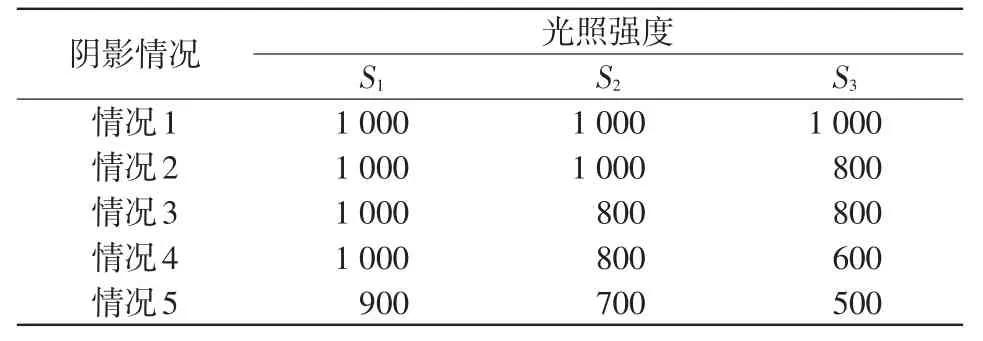
表1 不同阴影下各组件的光照强度Tab.1 Light intensity of each component under different shades W/m2

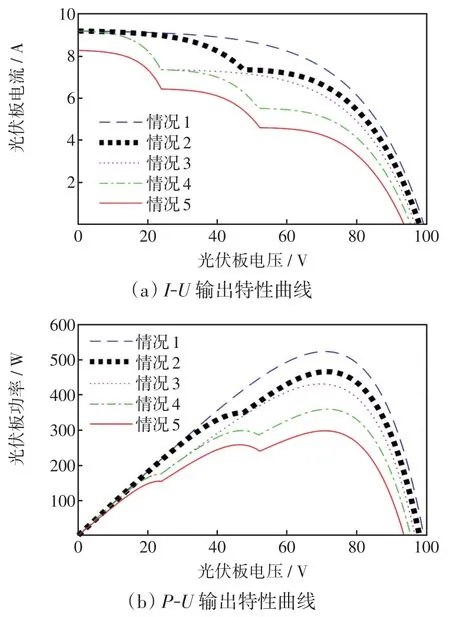
图1 不同光照下光伏阵列的输出特性曲线Fig.1 Output characteristic curve of photovoltaic array under different illumination conditions

由图1可见，在均匀光照的情况下，光伏阵列仅存在单个峰值点；情况2、情况3、情况4、情况5系统接收的光照不同，出现局部阴影；情况2和情况3系统的I-U曲线呈现双膝型，P-U曲线呈现双峰型；情况4和情况5系统的I-U曲线呈现三膝型，P-U曲线呈现三峰型。

由以上仿真结果可知，当光伏系统存在局部阴影情况时，其输出特性曲线会呈现多个局部极值点，若采用传统的MPPT算法，极有可能跟踪到的光伏系统的最大功率为局部最优值，进而导致MPPT失败。因此，本文提出一种基于改进型鲸鱼优化算法的MPPT控制策略，不仅能够加快算法的迭代速度，而且可以提升全局最大功率点跟踪能力，优化跟踪精度。

2 改进型鲸鱼优化算法在MPPT中的应用

2.1 基本鲸鱼优化算法

鲸鱼算法模拟了鲸鱼特殊的泡泡网觅食行为。鲸鱼算法主要由搜索觅食阶段、收缩包围阶段、螺旋更新位置阶段组成[7-8]。

2.1.1 搜索觅食阶段

在鲸鱼搜索食物的过程中，鲸鱼算法使每头鲸鱼按照彼此的定位进行随机搜寻。此阶段其数学模型为

式中：A和C为系数向量；t为当前迭代次数；Xrand（t）为从当前群体中随机选取的鲸鱼个体；X（t）为当前鲸鱼的个体位置；r1和 r2分别为[0，1]的随机数[9]；a为控制参数，随迭代次数的增加从2线性递减到0，即

式中，max_iter为最大迭代次数。

2.1.2 收缩包围阶段

当|A|＜1时，鲸鱼进入收缩包围阶段，全部的鲸鱼从各个位置共同游向目前位置最佳的鲸鱼。在此阶段，其数学模型为

式中，Xbest（t）为在当前所有鲸鱼群体中位置最佳的鲸鱼个体。

2.1.3 螺旋更新位置阶段

在此阶段，鲸鱼个体采用螺旋方式更新移动，逼近位置最佳的鲸鱼。此阶段其数学模型为

式中：D'为当前鲸鱼个体位置与最佳鲸鱼个体之间的距离；b为常量系数；l为[-1，1]之间的随机数。

鲸鱼算法3个阶段的选择取决于参数|A|和概率因子[9]P，当P≥0.5时处于螺旋更新位置阶段；当P＜0.5时处于其余2个阶段。其数学模型为

2.2 改进鲸鱼算法

传统鲸鱼算法应用于光伏最大功率点跟踪时，存在搜索速度慢、功率输出不平稳等问题，针对这些问题对鲸鱼优化算法进行改进。针对传统鲸鱼算法在局部寻优及全局寻优能力存在的弊端，引入了非线性收敛因子。为避免陷入局部最优，提高控制精度并且加快算法收敛速度，引入了非线性自适应权重因子。

2.2.1 Tent混沌映射

混沌具有遍历性和随机性等特点，根据这些特点来优化搜索，可以提升算法的寻优性能。与Logistic映射相比，Tent映射的混沌序列分布更为均匀，寻优速度更快，搜索效率更高。因此，本文的混沌序列由Tent映射产生，表示为

经伯努利移位变换后表示为

式中：xn为混沌值；mod为取余取模函数。Tent混沌映射可以使鲸鱼优化算法种群分布更为均匀，并使其拥有更广阔的搜索范围。

2.2.2 非线性收敛因子

线性收敛因子在均衡局部寻优能力和全局搜索能力方面存在弊端，所以，提出了一种非线性收敛因子，即

式中，μ和φ为其表达式的相关参数，μ=0.5，φ=0。

1995～2009年，中国各省财政转移支付/财政支出的全局Moran指数I亦均大于0，存在显著的空间正相关性。但其究竟是如何聚集的，全局性Moran指数I无法进行相关的分析，需要进行局部空间Moran指数LISA分析。1995年分税制改革初期，虽然中国地区间经济发展差距巨大，但过渡时期的转移支付制度仍留存有原财政体制的分配模式。除个别省份外，几乎不存在局部的空间聚集(见图4)。这一时期，转移支付制度仅作为原有财政分配制度的过渡，分配相对比较均衡，尚未带有较强的区域和政策导向性。

2.2.3 非线性自适应权重策略

为及时跳出局部最优，增强全局搜索能力，引入一种非线性时变的自适应权重策略，即

式中：w为自适应权重因子；h为调节系数，h=0.5。

在算法迭代初期，自适应权重因子较大，有利于提升全局的探索能力；在算法迭代后期，自适应权重因子减小，有助于跳出局部最优并且进一步提升鲸鱼算法的寻优精度。

当引进新的w后，式（2）和式（8）、式（9）分别更新为

2.3 改进型鲸鱼优化算法的光伏最大功率点跟踪

本文提出的改进型鲸鱼优化算法IWOA（improved whale optimization algorithm）是在传统的鲸鱼算法的基础上，引入了非线性收敛因子和非线性自适应权重策略。将光伏发电系统的输出功率作为目标函数，将鲸鱼的位置作为光伏电池某一点的输出电压，非线性收敛因子的引入不仅可以加快算法的收敛速度，而且可以提升全局最大功率点跟踪能力。非线性自适应权重因子能够让鲸鱼及时跳出局部极值，增强全局探索能力。通过改进鲸鱼算法搜索并更新鲸鱼的位置，从而更快速准确地跟踪到光伏系统的全局最大功率点电压，最终产生相应的占空比。和Boost升压电路结合，可以使光伏电池一直工作在最大功率点。

本算法的具体操作步骤如下。

步骤1对IWOA的相关参数初始化，设置种群数量N和最大迭代次数max_iter等。

步骤2利用Tent混沌映射在搜索空间中初始化位置分布相对均匀的N个个体。

步骤4对每头鲸鱼的适应度进行计算，比较和确定个体和全局极值。将鲸鱼当前适应度与最佳鲸鱼的适应度相比对，若当前适应度大，则保留适应度高的鲸鱼位置，将其适应度视为新的最佳，之后再将每个鲸鱼的适应度与鲸鱼群体最优适应度相比对，则保留鲸鱼群体的最优适应度，并及时更新适应度最佳的鲸鱼位置。

步骤5更新鲸鱼的位置，使之朝着最大功率点方向靠拢，利用式（14）执行随机的搜索觅食，利用式（16）执行收缩包围和螺旋更新位置。

步骤6检查是否满足结束条件。若满足，则停止迭代，此时即得到全局最大功率点电压；反之，重新计算适应度。

3 仿真实验与分析

为了验证改进型鲸鱼算法应用于光伏多峰值跟踪的优越性、可靠性，依次在静态阴影和动态阴影2种情况下进行仿真研究。为了保证能采集到下一个搜索步骤前光伏阵列的输出功率，将采样时间设定为1 ms。仿真模型如图2所示。

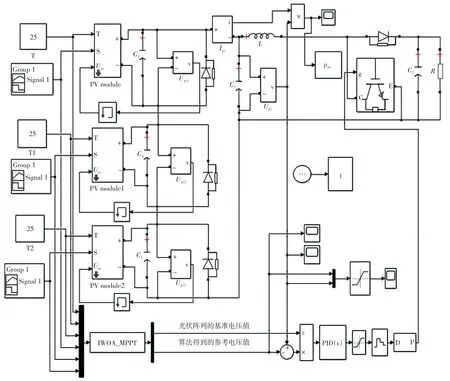
图2 基于改进鲸鱼优化算法的光伏系统MPPT仿真模型Fig.2 MPPT simulation model of photovoltaic system based on improved whale optimization algorithm

选取的某型号光伏电池的参数如表2所示。

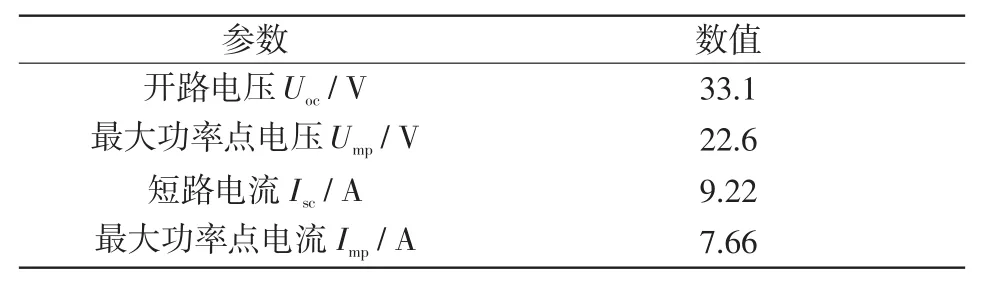
表2 光伏电池的参数Tab.2 Parameters of photovoltaic cells

3.1 静态阴影

在静态阴影情况下，为了验证改进新型鲸鱼算法应用于多峰值最大功率点跟踪时的可靠性及优越性，分别在双峰值、三峰值2种情形下进行仿真对比测试。将双峰值下的种群数量、迭代次数分别设置为10、30；将三峰值下的种群数量、迭代次数分别设置为30、60。

工况1：当处于双峰值情况、温度为25℃时，光伏阵列的光照强度依次设置为1 000、800、1 000 W/m2，其输出特性曲线如图3所示。

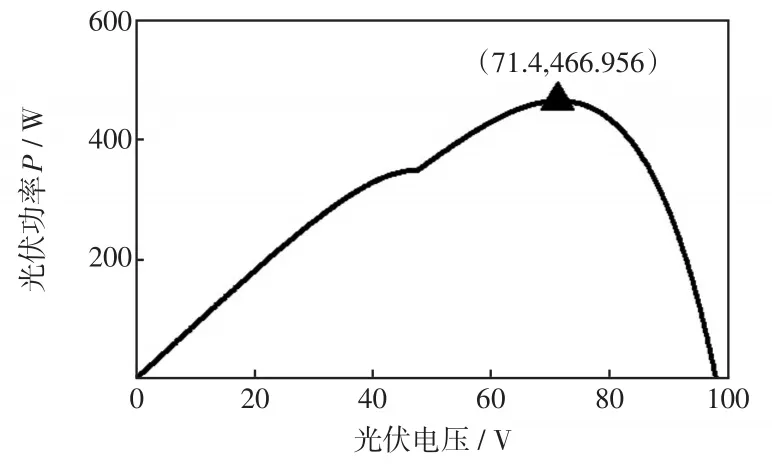
图3 光伏阵列的双峰值曲线Fig.3 Double-peak curve of photovoltaic array

由图3可见，在工况1情况下，光伏阵列的输出最大功率为466.956 W。

在工况1条件下，通过将PSO算法、LSO算法、WOA、IWOA进行仿真对比，来验证改进型鲸鱼算法IWOA的优劣性。迭代寻优结果如图4所示。

从图4可见，PSO算法迭代速度慢，且输出不稳定，第5次时容易陷入局部极值，迭代到第26次时才跟踪到最大功率点；LSO算法迭代22次左右搜索到功率最大值，迭代速度较慢；WOA迭代至第2次易陷入局部极值，迭代至第11次左右搜索到功率最大值；IWOA只需迭代3次左右就可搜索到功率最大值并且趋于稳定。IWOA搜索到的最大功率更接近理想功率。通过对比仿真曲线可知，相比于PSO算法、LSO算法、WOA，IWOA具有更快的迭代速度，跳出局部最优的能力更强，全局寻优能力更强，且能更准确地搜索到最大功率点。

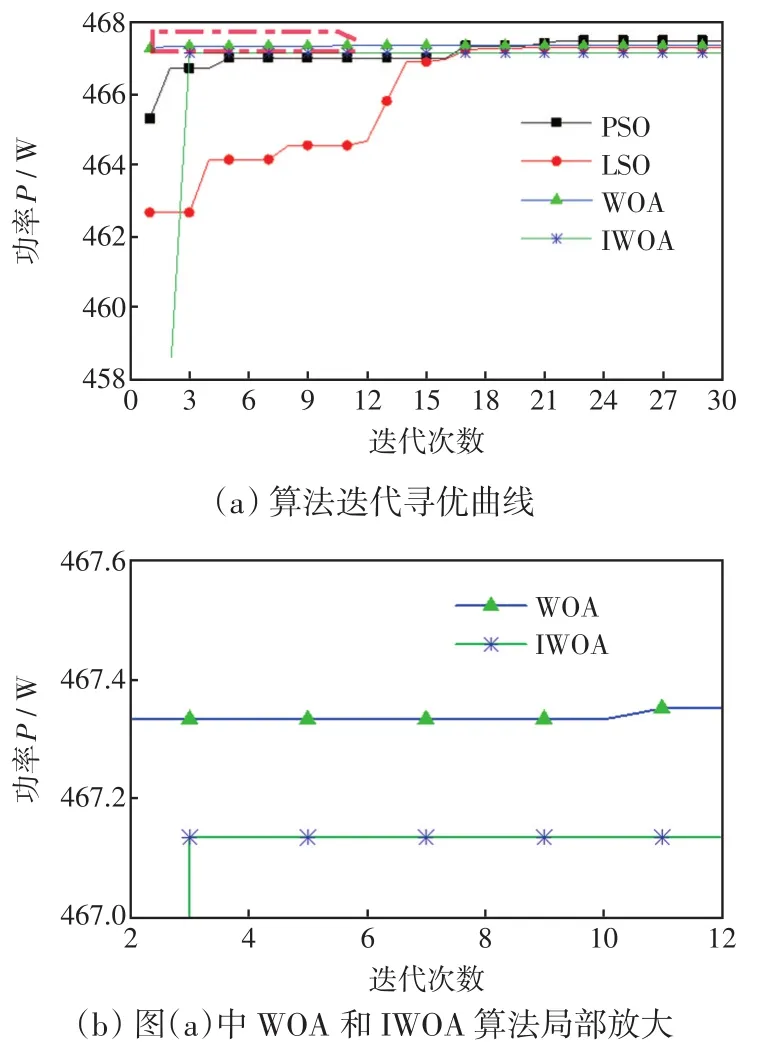
图4 4种算法在双峰值下迭代寻优结果Fig.4 Iterative optimization results of four algorithms under double-peak

在工况1的双峰值条件下，功率-时间追踪曲线如图5所示。

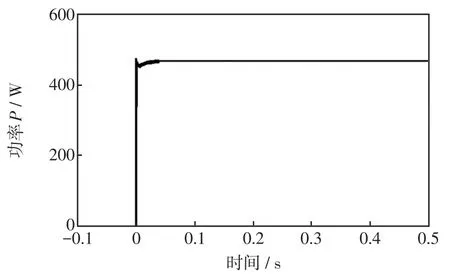
图5 工况1的功率-时间追踪曲线Fig.5 Power-time tracking curve under working condition 1

由图5可见，经过0.039 s，IWOA跟踪到最大功率点，其最大功率为467.36 W。IWOA不但跟踪时间较快，而且能提升全局最大功率点跟踪能力。

工况2：当处于三峰值情况、温度为25℃时，光伏阵列的光照强度依次设置为1 000、800、600 W/m2，其输出特性曲线如图6所示。

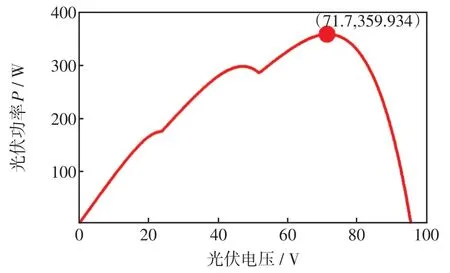
图6 光伏阵列的三峰值曲线Fig.6 Three-peak curve of photovoltaic array

由图6可知，在工况2情况下，光伏阵列的最大输出功率为359.934 W。

在工况2条件下，通过将PSO算法、LSO算法、WOA、IWOA进行仿真对比，来验证改进型鲸鱼算法IWOA的优劣性。迭代寻优结果如图7所示。

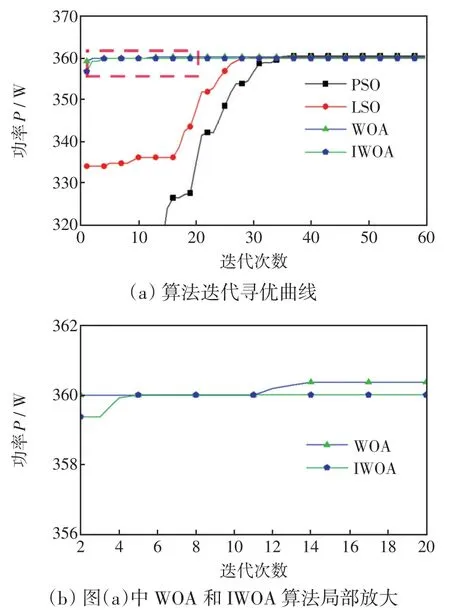
图7 4种算法在三峰值下迭代寻优结果Fig.7 Iterative optimization results of four algorithms under three-peak

从图7可见，PSO算法迭代至第36次左右才追踪到最大功率点，迭代速度较慢，且输出不稳定，LSO算法迭代30次左右搜索到功率最大值，且容易陷入局部极值，WOA迭代至14次左右搜索到最大功率值，且容易陷入局部极值；IWOA迭代至第5次左右就可搜索到功率最大值且趋于稳定；4种算法搜索的最大功率值近似。通过对比仿真曲线可知，相比于PSO算法、LSO算法、WOA，IWOA具有更快的迭代速度，跳出局部最优的能力更强，全局寻优能力更强，且能更准确地搜索到最大功率点。

在工况2的三峰值条件下，功率-时间追踪曲线如图8所示。

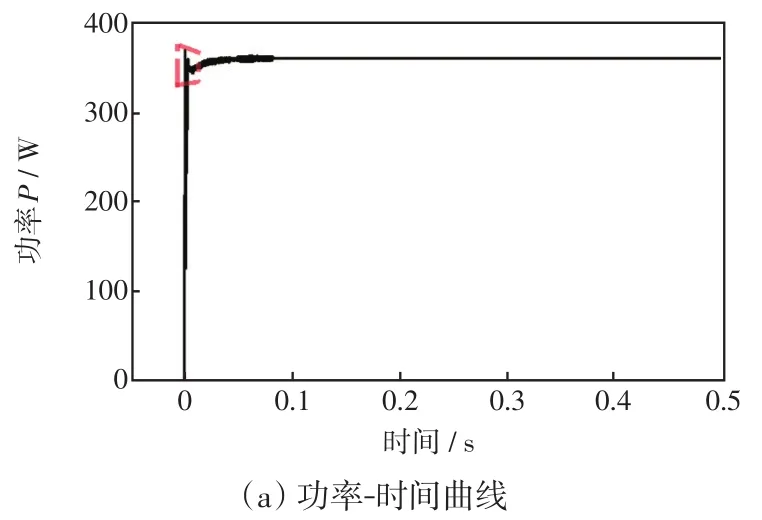
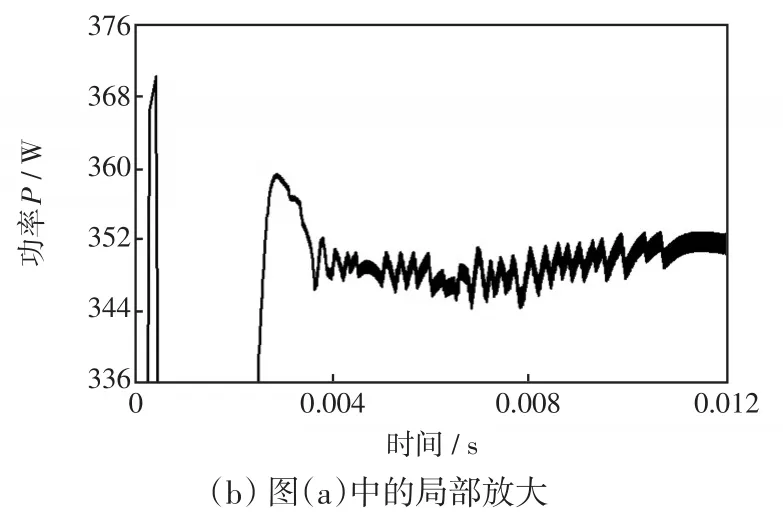
图8 工况2的功率-时间追踪曲线Fig.8 Power-time tracking curve under working condition 2

由图8可见，经过0.076 s左右，IWOA跟踪到最大功率点并达到稳定，其最大功率为360.361 2 W，与理想最大功率点仅差0.427 2 W。IWOA不仅跟踪时间快，而且能避免陷入局部极值，使之可以高精度地跟踪到全局最大功率点。

3.2 动态阴影

在实际应用中，光伏阵列接收的太阳辐射是不断变化的，因此，有必要在动态阴影条件下验证改进型鲸鱼算法的有效性。对动态阴影下仿真条件进行设置，起始时为情景1：3块光伏组件的光照强度依次为 S1=1 000W/m2、S2=800W/m2、S3=1 000W/m2；在0.1 s时，光照强度突然发生阶跃变化为情景2：3块光伏组件的光照强度依次为S1=1 000W/m2、S2=800W/m2、S3=600W/m2；在0.5 s时，光照强度突然发生阶跃变化为情景3：3块光伏组件的光照强度依次为900 W/m2、700 W/m2、500 W/m2。图9为光照强度从情景1变化到情景3的光伏发电系统理论输出的功率最大值。图10为光照强度从情景1变化到情景3的最大功率点跟踪仿真效果。

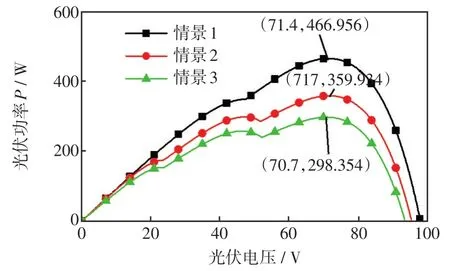
图9 功率特性曲线Fig.9 Power characteristic curve

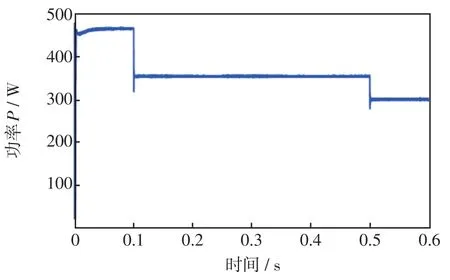
图10 功率跟踪效果Fig.10 Power tracking effect

由图9可见，光伏组件在情景1时，光伏发电系统的最大输出功率理论值为466.956 W；在0.1 s时，光照强度突然发生阶跃变化为情景2，光伏发电系统的最大输出功率理论值为359.934 W；在0.5 s时，光照强度突然发生阶跃变化为情景3，光伏发电系统的最大输出功率理论值为298.354 W。

由图10可见，光照强度在情景1时，经过0.031 s后，光伏发电系统的输出功率最大值稳定在468.92 W左右，该算法的跟踪精度约为99.6%；光照强度突变到情景2时，该算法经过0.036 s左右搜索到最大功率点，输出功率的最大值为361.6 W，该算法的跟踪精度约为99.5%；在0.5 s时，光照强度突变为情景3，该算法大约用了0.029 s搜索到最大功率点，输出功率的最大值为300.6 W，该算法的跟踪精度约为99.3%。经过上述分析可知，当光照强度突然发生阶跃变化时，该算法响应速度快、暂态过程短，可以高效率地跟踪到最大功率点。

4 结论

为解决局部遮阴等复杂工况下的光伏多峰跟踪问题，本文提出一种基于改进鲸鱼算法的MPPT控制，通过Tent混沌映射增加种群多样性，通过引入非线性收敛因子及非线性自适应权重策略提升全局搜索跟踪能力，并加快迭代速度。经过与粒子群算法、狮群算法、传统的鲸鱼算法的对比仿真验证，得到以下结论。

（1）所提的改进型鲸鱼算法具有更快的追踪速度和更高的寻优精度，可以在局部遮阴等复杂工况下高效率地工作。

（2）所提算法能避免陷入局部最优，能改善传统鲸鱼算法收敛后功率输出不稳定的弊端。

（3）所提算法在静态及动态多峰的情况下，可以高效率、高精度地追踪到最大功率点。