基于图注意力网络的配电网超分辨率量测生成方法

吕奇峰，陈 颖，肖谭南，于智同，宋炎侃，朱 童

（1.清华大学电机工程与应用电子技术系，北京市 100084；2.清华四川能源互联网研究院能源电力系统数字孪生研究所，四川省 成都市 610042；3.国网四川省电力公司，四川省 成都市 610042）

0 引言

在实现“碳达峰·碳中和”目标牵引下，可再生能源与电动汽车等柔性负载将大量接入配电网，导致配电网结构更加复杂。准确、快速的运行状态感知，对于配电网安全、经济、低碳运行至关重要［1-2］。

配电网量测主要由数据采集与监控（supervisory control and data acquisition，SCADA）系统管理，采样频率和量测精度都较低。为了获得高精度的稠密量测，有研究提出了配电网相量量测方法。但相量量测单元（phasor measurement unit，PMU）成本较高，无法大规模部署。因此，配电网状态量测呈现布局不均、精度不足的特点，量测结果时空稀疏度高［3-4］。

传统状态估计要求输入量测具有冗余度，通过迭代估计出满足电路定律的潮流分布。然而，实际配电网的量测时空稀疏度高，可能无法满足状态估计的冗余度要求，难以实现全面准确感知［5-6］。为此，有必要研究配电网状态的超分辨率生成方法，即利用稀疏量测数据，通过神经网络生成缺失量测信息，提高配电网状态感知分辨率。

已有研究探索了配电网量测生成技术。文献［7］提出了带有跳过连接架构的深层神经网络（deep neural network，DNN），称为Prox-Linear net，以模仿Prox-Linear 求解器的状态估计算法，优于广泛采用的Gauss-Newton 状态估计求解器。文献［8］从时空图角度提出基于时空特征图卷积网络的动态状态估计算法，提取量测数据的时空和节点的特征信息，融合得到实时状态估计结果并可以消除不良数据的影响。文献［9］利用配电网状态估计的近似可分离性，优化PMU 的布点，改进了拓扑感知DNN的设计，具有较强的鲁棒性。

上述研究以状态估计作为提高系统态势感知的方法，难以在量测时空分辨率较低的配电网广泛应用［10-11］。配电网拓扑作为一种图结构，由电气节点和导线支路组成，蕴含了丰富的图信息。随着图神经网络的出现，将较为成熟的神经网络扩展到了图域中，实现了深度学习与图数据的结合。目前，应用最广泛的图神经网络主要有图卷积网络（graph convolutional network，GCN）［12］和 图 注 意 力 网 络（graph attention network，GAT）等［13］。文献［14］利用GCN 对配电网进行量测超分辨率补全，充分考虑节点之间的联系和影响，提高了配电网量测在时间和空间上的分辨率。与GCN 在谱域进行卷积不同，GAT 通过引入注意力机制实现空域上的信息聚合，使模型更加关注邻居节点间的相互影响。因此，GAT 更适用于拓扑变化频繁的配电网态势感知。

针对配电网状态监测数据时空分辨率较低、配电网拓扑频繁改变的问题，本文提出了一种可以适应配电网拓扑变化的加入物理约束的图注意力网络（physics-informed graph attention network，PIGAT）。该方法将配电网潮流约束加入图注意力网络的训练过程中，利用注意力机制挖掘拓扑中的节点状态关联性，构建包含全部图连接关系的训练拓扑集进行训练，并根据拓扑邻接矩阵变化自适应生成新的网络参数，实现配电网量测最小化采集的状态及时感知，增强模型在超分辨率生成数据方面的拓扑泛化能力。

1 问题建模

1.1 配电网量测时空分辨率

受限于设备性能和投资成本，配电网量测配置分布不均现象显著，电气节点量测采样的周期、量测精度及同步性等方面存在较大差异［15］。

PMU 量测频率一般在20～100 Hz，传输间隔根据需求设置在数秒至数分钟之间［16］，数据传输时延小、精度高，可以直接测量节点电压相量和支路电流相量，但受限于PMU 较高的配置成本和通信压力，配置PMU 的节点比例一般在20%左右。SCADA系统量测频率一般在0.1～5.0 Hz，传输间隔一般设置在数分钟，数据传输时延大、精度低，测量值包括节点注入功率、支路功率和电压幅值。SCADA 系统量测一般可以满足配电系统的拓扑可观性。高级量测体系（advanced metering infrastructure，AMI）通常包含智能电表量测，量测频率一般不超过1 Hz，传输间隔一般为15 min［17］。

通常，在某一时刻，只可获得部分电气节点的量测数据。为了获得全网同步量测断面，需要根据已知电气节点状态生成未量测电气节点状态。超分辨率量测是从计算机视觉中引申来的概念。图像超分辨率［18］是指从一幅低分辨率图像或图像序列恢复出高分辨率的图像或图像系列。类似地，在配电网态势感知中，超分辨率量测是指从稀疏量测中恢复出更为稠密精细的配电网状态信息。如图1 所示，当实测和生成的电气节点状态具有较高的空间和时间分辨率，即所有电气节点状态均以较高采样率和精度被生成时，则得到了配电网超分辨率量测数据，可支撑配电网精细化运营管理和态势感知。

图1 空间分辨率提升示意图Fig.1 Schematic diagram of spatial resolution improvement

1.2 超分辨率状态生成数学建模

由于配电网中不同量测的时空分辨率不同，实际配电网需要完成的是基于多源稀疏量测的时序状态感知。对应的多源量测矩阵z如式（1）所示，包含了SCADA 系统和PMU 等多种量测系统的数据。

式中：zN(tn)为节点N在tn时刻的量测数据；ϕ为状态变量，表示当前时刻该位置没有量测数据。

由式（1）可知，配电网的量测数据在时空分布上具有很高的稀疏性。为了获得高分辨率的配电网状态矩阵，即节点电压矩阵V和节点相角矩阵θ，表达式分别如式（2）和（3）所示。

式中：VN(tn)和θN(tn)分别为节点N在tn时刻的节点电压和相角。

此时的时空状态感知即为求解与量测向量加权欧拉距离最近的理论值向量所对应的电压和相角，表达式为：

式中：h(·)为计算对应量测值的理论函数，包括节点注入功率计算公式、线路潮流计算公式等；Η(·)为量测权重矩阵函数；Vi(t)为t时刻节点i的电压；V(t)为t时刻两节点电压；Ninj为注入节点总数；Pinj(t)和Qinj(t)分别为节点在t时刻的注入有功和无功功率；Pline(t)和Qline(t)分别为线路在t时刻的支路有功和无功功率；Gik(t)和Bik(t)分别为t时刻拓扑节点i和k间导纳矩阵的实部和虚部；θik(t)为t时刻拓扑节点i和k间的相角；//为矩阵拼接符号。

传统状态估计可以通过冗余的量测数据迭代计算生成完整的状态数据，但对数据质量要求高。当存在不良数据时，会使状态估计的结果精度下降且计算耗时较长，无法满足状态及时感知要求。

事实上，历史量测数据与状态向量之间存在关联关系，可通过神经网络拟合其概率分布模型，通过输入部分量测数据，生成完整的状态向量，表达式为：

式中：p(V，θ∣z)为状态向量V、θ与量测z的条件概率模型；p(z)为量测z的概率分布模型。

状态感知的输入变量属于非欧氏空间的图数据，既有拓扑中节点的量测数据，也有拓扑中节点之间的连接矩阵。常用的卷积神经网络方法忽略了图结构信息，使状态感知精度难以进一步提高。同时，已有的配电网量测分辨率增强方法往往针对单一拓扑设计，当拓扑结构发生改变时，已有方法会因为无法适应新的拓扑而大大降低数值精度或出现潮流流向错误。由于配电网的拓扑可能会出现频繁的变化，针对原拓扑的量测设备布局可能无法很好适应新的拓扑结构，原来可观测的节点会变得不可观测。为了提高超分辨率方法的鲁棒性和通用性，应当设计具有拓扑泛化能力的超分辨率量测生成网络，适应于配电网重构拓扑场景。

2 用于超分辨率状态生成的GAT

2.1 GAT 原理

GAT 可以通过图节点之间的消息传递来表达节点相互依赖关系，具有精度高和泛化能力强的优点。同时，GAT 中引入了注意力机制，对消息传递参数赋予不同的权重。GAT 通过训练更新注意力参数实现相邻节点信息的有效聚合。上述消息传递和注意力机制是网络中的局部运算。当图拓扑改变后，GAT 可以自适应调整注意力参数，适应新的图拓扑，表现出良好的信息聚合和图特征学习效果［19］。

采用GAT 实现配电网超分辨率状态生成，通过注意力机制学习相邻电气节点状态相关性特征，并在配电网重构后自适应调整节点间注意力参数，增强了超分辨率状态生成模型的拓扑泛化能力。

2.2 配电网超分辨率状态生成GAT

配电网拓扑可以用一个无向图G={nN，E，A}表示，其中，nN为配电网节点集合，E为配电网边集合，A为邻接矩阵。拓扑中的节点由配电网电气节点组成，边由架空线路或电缆线路组成。

将时空稀疏量测数据作为GAT 的输入特征向量z=[z1，z2，…，zN]，聚合邻居节点信息后可以得到输出向量

GAT 通过将共享权重参数矩阵W应用在每一个节点上，实现共享的节点注意力机制a(·)并计算节 点 之 间 相 关 度eij=a(Wzi，Wzj)，eij表 示 节 点j对节点i的影响程度。将所有与节点i连接节点的相关度计算后，使用SoftMax 函数进行归一化得到注意力系数矩阵α，其元素αij的表达式为：

式中：LeakyReLU(·)为激活函数。

至此，将拓扑中所有与节点i相邻节点的时空稀疏量测输入zj，按照注意力系数分配的权重即可完成信息聚合得到输出特征向量的元素z′j为：

式中：σ(·)为激活函数。

注意力机制通过对关注事物的不同部分赋予不同的权重，从而降低其他无关部分的作用。如附录A 图A1 所示，GAT 针对配电网中每个节点和其相邻节点，通过训练更新注意力参数矩阵，实现邻居节点的信息聚合。由于输入量测数据的低时空分辨率，在一个时空断面上没有量测的节点可以通过其邻居节点的量测而获得数据。对于因配电网重构而发生的拓扑改变，GAT 可以做到自适应分配新的注意力参数矩阵，对新拓扑依然可以做到良好的数据聚合。

GAT 通过注意力机制解决了GCN 对同阶邻域节点只能分配相同权重的问题，改变了其每次更新整个配电网拓扑图操作的方式，更加注重于邻居节点的电气特征。在配电网拓扑结构变化时，可以自适应调整节点之间的注意力系数，增强了模型在不同结构配电网上的泛化能力。

2.3 考虑潮流约束的超分辨率方法

传统的神经网络训练一般通过计算输出与真值的均方误差（mean square error，MSE）作为损失函数，表达式为：

式中：Lmse为MSE 的值；n为样本统计总数；Xm为样本m的真值；X̂m为样本m的预测值。

使用MSE 作为损失函数使样本输出不断逼近样本真值，保证了模型对于输出结果的高数值精度。但对于一段时空中的电气状态量x是一个多维矩阵，表达式为：

式中：θi(t)为t时刻节点i的相角。

在训练过程中有无数组可行的W可以使输出结果陷入局部最优解，从而得到一组较小的MSE 满足模型的数值精度要求。然而，训练所得模型可能不满足实际潮流约束，出现对训练样本过拟合，弱化了模型拓扑泛化能力［20］。因此，超分辨率生成模型训练中应考虑物理约束，即要求节点状态量要满足的潮流平衡方程［21-22］，如式（10）和式（11）所示。

具体地，通过超分辨率生成的V和θ，可以计算得到节点i注入的有功功率pi(V//θ)和无功功率qi(V//θ)。将pi(V//θ)、qi(V//θ)和节点i注入有功真值和无功真值做差，可以得到超分辨率网络的潮流残差矩阵g(V//θ)为：

取g(V//θ)的绝对平均值作为潮流损失函数Lphy加入网络训练过程中，与Lmse共同构成神经网络的损失函数。这样不仅可以提高超分辨率生成数据精度，也可以让生成的数据满足电气物理规律，避免落入局部最优解。

综上，加入潮流约束的图注意力超分辨率模型的求解过程可以归纳为寻找同时满足数值精度要求和潮流损失要求的共享权重参数矩阵W。

式中：G为训练拓扑集数量；Xij为节点i和j间的潮流状态量真值；sij为节点i和j间的潮流复功率；Y为拓扑的节点导纳矩阵；Y*为Y的伴随矩阵；λ为物理约束的权重系数，其数值随着训练轮数逐渐提高；⊙为矩阵对应元素相乘的符号。

2.4 PI-GAT 的网络结构

由于邻接矩阵A的稀疏性，PI-GAT 中每层网络可以向外传播1 阶邻节点信息，w阶邻节点仅在第w次层间传播后才可以互相感知。当网络层数过小时，离量测数据节点较远的节点无法充分信息聚合；当网络层数过大时，信息传递出现均质化并且增大训练难度和训练时长。根据算例使用的配电网量测布局，确定量测时空分布中与量测节点最远的无量测节点即可确定网络层数。附录B 表B1 给出了本文使用的网络模型结构。

2.5 PI-GAT 训练方法设计

为了使PI-GAT 模型更好地应对可能会出现的各种重构拓扑，有必要将使模型掌握尽可能多的拓扑连接关系。但当拓扑规模较大时，重构拓扑数量呈指数型增长，若将所有拓扑均纳入训练集中，势必会构成难以克服的训练障碍，大大降低训练效率。为此，对PI-GAT 的训练方法进行了设计改进，使模型以较小的训练成本完成所需要的数据精度要求。

配电网的原拓扑与重构拓扑可以构成一个拓扑集合。对于拓扑集合中每条有联络开关的线路，需要在训练过程中让PI-GAT 模型学习线路所连接的节点之间的状态相关性。通过这样训练，一方面可以让模型掌握所有可能会出现的节点相互影响关系，另一方面也可以让系统更好应对未知的潮流方向。为此，可以构建一个由原拓扑和单一联络开关改变的重构拓扑的训练拓扑集合Gset，如式（14）所示。

因此，在训练过程中，任意两个节点间可能出现的连接关系均被训练集Gset所包含，进而当出现未出现在训练集中的系统拓扑出现时，所提模型可动态生成有效的注意力系数αij。PI-GAT 超分辨率模型示意图如图2 所示。

图2 PI-GAT 超分辨率模型示意图Fig.2 Schematic diagram of PI-GAT super-resolution model

3 算例分析

本文以IEEE 33 节点配电网系统作为测试算例，如 图3 所 示 共 有4 条 馈 线、33 个 节 点 和32 条 支路，每个节点均有负载或分布式电源接入。该系统中节点1 为父节点，节点8-21、9-15、12-22、18-33 和25-29 之间均有重构联络开关。

图3 IEEE-33 节点配电网拓扑Fig.3 Topology of IEEE 33-bus distribution network

3.1 算例设计

本文将拓扑中与多条馈线或重构线路相连的节点定义为支路节点，将在拓扑中只与一个节点相连的节点定义为末端节点。考虑到支路节点在拓扑中可以聚合更多的拓扑信息，将支路节点均配备PMU，数据传输间隔为1 min。末端节点可以提供关键的末端潮流数据和拓扑结构变化信息，更好应对拓扑变化时出现的潮流反转情况，将末端节点均配备AMI，数据传输间隔为15 min。非支路节点和末端节点的拓扑节点可以考虑配备SCADA 系统，数据传输间隔为5 min 或不设置量测。量测设备配置方案如表1 所示。本文以数据传输的时间为量测时标，根据时标信息即可构建量测矩阵，将64 帧内收集的量测数据归为一个时空片段量测数据集。

表1 量测设备配置方案Table 1 Configuration scheme of measurement equipment

将IEEE 33 节点算例在MATPOWER 中根据重构开关的不同组合，生成6 种重构拓扑的24 h 潮流稳态数据。在此基础上，添加标准差为0.1 的高斯扰动，以进一步模拟实际负荷的波动特征。潮流数据包含算例各节点的节点电压幅值、相角、节点注入有功功率和无功功率。将潮流数据以64 帧的时间长度切割并和重构拓扑关联矩阵一起打乱作为数据样本集。将样本集按照8∶1∶1 的比例划分训练集、验证集和测试集，其中，训练集有4 000 个样本，验证集和测试集各有500 个样本。为了测试本文方法对于未训练过的拓扑时的超分辨率拓扑泛化能力，额外生成了6 种拓扑和潮流数据作为拓扑泛化测试集，各有500 个样本。所提方法在Pytorch 上搭建PI-GAT，并采用Adam 优化器在GPU（型号为RTX3060）上训练1 000 轮，设定小批量（mini-batch）的规模为32，初始学习率为0.000 1，学习率每100 轮下降1 次。

3.2 评价指标

本文所提方法在训练过程中使用的损失函数L(s，v，̂，Y，λ)由两部分组成，表达式为：

式中：v和̂分别为超分辨率量测输出和潮流真值；s为潮流复功率。

3.3 拓扑泛化测试

为了测试本文方法的拓扑泛化能力，将所提模型与线性插值、3 次样条插值及GCN 进行了对比，如附录A 图A2 所示。PI-GAT 模型在训练200 轮时可以快速达到一个较小的值，并随着训练轮数增加而持续下降。

PI-GAT 模型对7 种拓扑测试的指标结果如表2 所示。表中：Ltotal为总损失。对于所有拓扑均可以根据低分辨率量测生成非常高准确率的超时空分辨率数据。由于配电网重构，会导致拓扑中原有的潮流流向发生改变，如馈线19-22 会连接节点2 或节点12，而这两种情况下的潮流流向是截然相反的。同样，在训练集拓扑6 中，节点33 也会因为拓扑重构与节点18 相连接，这与其他训练样本的潮流流向出现明显不同。

表2 7 种拓扑各项指标结果Table 2 Results of each index in seven topologies

PI-GAT 模型用两种不同损失函数训练时，对于泛化测试拓扑6 的指标结果如表3 所示。由于泛化测试拓扑6 相对于训练集的拓扑改变程度较大，并且出现了馈线26-29 由节点25 接入的新潮流方向。由表3 可知，只使用MSE 作为损失函数的PIGAT 模型，虽然准确率依然较高，但也出现了明显的准确率下降。在潮流方向改变的线路，所生成节点电压差异依然保持与训练集拓扑一致，违背了新潮流方向。在将潮流约束加入损失函数后，PIGAT 模型泛化能力进一步提高，准确地反映了潮流方向改变，提高生成量测精度。

总之，我们认为，内源激素GA3、ABA和IAA在龙牙百合鳞茎休眠的整个过程中起着重要的调控作用。但是激素的作用机理是十分复杂的，休眠的调控不仅与植物内源激素的绝对含量有关，也与植物组织或器官对内源激素的敏感性有关，更与各类激素之间的平衡，特别是促进生长类激素与抑制生长类激素之间的比例及平衡有关。对休眠解除期间各类内源激素的具体相互协作关系，还有待进一步从分子生物学层次进行研究。

表3 加入潮流约束的模型泛化测试结果Table 3 Generalization test results of model with tide constraints

进一步，图4 给出了针对泛化测试拓扑6 的某单次生成测试部分结果，即节点5 和节点27 的节点电压-时间变化曲线。其中，节点5 的量测传输间隔为5 min，节点27 的量测传输间隔为15 min。可以看出，PI GAT 模型在应用于未经过训练的新拓扑时，依然可以生成较为精准的超分辨率量测。

图4 节点5 和27 的PI-GAT 节点电压超分辨率结果Fig.4 Super-resolution results of PI-GAT bus voltage for bus 5 and bus 27

在统计了泛化测试拓扑6 中32 000 个潮流断面的各节点电压误差后，绘制了节点电压相对误差箱形，如图5 所示。图中：虚线上端横线和下端横线分别表示统计样本中最大误差和最小误差，红色横线为统计样本误差中位数。由图5 可知，加入了潮流约束的PI-GAT 模型在应对拓扑改变程度较大的测试拓扑6 时，依然可以将整体误差控制在很小的范围内。但需要注意到，潮流方向的大幅变化依然会提高关联节点电压的相对误差。馈线11-14、12-22、26-29 和29-32 均发生了潮流方向改变，输出结果虽然反映了真实潮流方向，但量测生成精度有所下降。

图5 泛化测试拓扑6 中节点电压相对误差箱形图Fig.5 Box plot of bus voltage relative error in generalized test topology 6

附录A 图A3 对比了PI-GAT、GCN、线性插值和样条插值在泛化测试拓扑6 节点16 的超分辨率结果。由图A3 可知，当测试拓扑相对训练拓扑集改变较大时，考虑潮流约束的PI-GAT 模型依然可以准确跟踪潮流变化，而GCN 模型结果与真实值之间存在较大误差。另外，由于两种插值方法不需要考虑拓扑变化，只需要在量测输入点之间插值即可，补充的数据虽然与实际值差距不大，但不能准确反映较长量测时间间隔中的潮流变化趋势。

图6 对比了不同方法超分辨率量测生成精度，本文提出的加入潮流约束的PI-GAT 模型对于拓扑的变化具有很强的泛化能力，可以适应不同改变程度的拓扑结构并保持很高的准确率。GCN 模型对于拓扑的变化也具有一定的适应性，当测试拓扑改变不大时可以提供较准确的数据结果。但当拓扑改变逐渐变大时，其输出结果准确性显著下降。两种插值方法可不依赖拓扑矩阵进行数据生成，但数据精度无法提高。

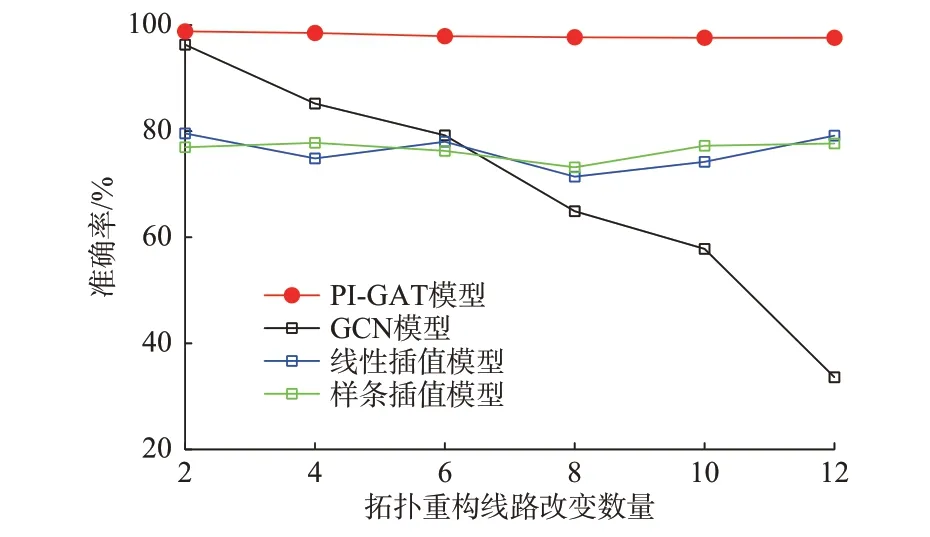
图6 4 种模型在不同拓扑重构线路数量下的准确率Fig.6 Accuracy of four models with different numbers of topologically reconfigured lines

3.4 大规模系统测试

由于算法的输入特征，例如关联矩阵与稀疏量测均为高度稀疏矩阵，当系统规模变大时，所占用的计算资源并不会指数增长。模型训练的基本要求为所有可能接入的线路在训练集中均有接入即可，无需反复重构拓扑作为训练集。因此，本文算法在更大规模的配电网系统中依然具有适用性。

为了验证所提算法和模型在更大规模配电网系统时的效率和准确性，本文对IEEE 123 节点配电网算例［23］进行了相关测试。在MATPOWER 中生成原拓扑及4 种系统重构拓扑的24 h 潮流数据，并根据潮流数据按照8∶1∶1 的比例划分训练集、验证集和测试集。5 种拓扑各项指标结果如表4 所示。

表4 5 种拓扑各项指标结果Table 4 Results of each index in five topologies

附录A 图A4 给出了5 种拓扑的PI-GAT 模型生成的节点电压值与实际值之间的相对误差平均值，可以看出所生成超分辨率量测结果依然保持较高数值精度。

需要指出的是，上述测试中，每份超分辨率数据生成时间约为4.5 ms，而系统状态估计所需耗时约为10.0 ms。可见，PI-GAT 模型生成超分辨率状态只需进行前向推断，无需迭代计算，执行效率较高，适用于电网在线分析场景。

4 结语

由于配电网中随机性和不确定性因素不断增加，配电网监控需要提高量测的时空分辨率，以满足全方面准确掌握系统运行状态的要求。本文的主要贡献有以下几点：

1）以提高系统整体量测数据分辨率为出发点，针对现有的基于神经网络和数值插值的量测数据补充方法泛化能力差、精度不足等问题，提出了基于加入潮流约束的GAT 模型的配电网适应性超分辨率方法，在模型中将MSE 和潮流残差共同作为损失函数，引入PI-GAT 学习量测时空信息映射关系，通过最小化量测实现及时状态感知。

2）比较了提出的PI-GAT 模型与GCN、线性插值和样条插值模型在数值精度和泛化能力上的差异，得出PI-GAT 不仅具有更高的数值精度而且对于拓扑改变具有更强的泛化能力的结论。对比了在损失函数中加入潮流约束与未加入潮流约束的泛化结果，验证所提方法具有更强的拓扑适应能力。

目前，本文提出的PI-GAT 模型以系统仿真潮流数据为数据集，通过离线训练参数，在线生成超分辨率数据，可以大幅提高量测数据时空分辨率并提高准确性，而且可以适应配电网重构带来的拓扑变化。下一步研究中，可以针对实际配电网拓扑识别不准确以及量测数据时标不统一等问题展开，并对模型训练样本生成方法进行设计和改进，提高模型训练效率和适应性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。