面向复合地图的移动机器人分层路径规划
武 星 杨俊杰 汤 凯 翟晶晶
楼佩煌南京航空航天大学机电学院,南京,210016
0 引言
路径规划是移动机器人研究的重点领域,其主要目的是在给定环境下搜索出一条从起点到终点的优化路径,该路径在不与障碍物碰撞的前提下,尽量保证行驶距离最短、安全性最高、行驶时间最优等一个或多个性能指标[1-2]。根据对环境信息的认知程度,路径规划可分为两类:对环境有完整认知的全局路径规划、环境未知或动态变化的局部路径规划[3-4]。前者旨在利用全局视野寻找一条全局优化路径,后者旨在躲避障碍物,修正全局路径。环境建模是机器人理解周围环境的重要途径,也是全局路径规划的前提,常用的环境地图有栅格地图[5-6]、可视图[7]、拓扑地图[8]。
随着移动机器人工作空间的不断扩大以及作业场景的日益复杂化,跨车间配送、非预期障碍物等因素增加了路径规划的难度。现有的全局路径规划方法如A*算法[9-10]、蚁群算法[11-12]、粒子群算法[13]、遗传算法[14-15]等常因搜索空间的膨胀导致搜索效率急剧降低,甚至无法搜索到最优解。传统局部路径规划方法如人工势场法(artificial potential field, APF)[16]、动态窗口法(dynamic window approach, DWA)[17]等存在易于陷入局部极值点、避障实时性及成功率不高等问题。
针对部分未知的复杂大场景环境,余翀等[18]提出一种分层次多步骤的路径规划算法,首先在拓扑层规划,采用起泡算法生成Voronoi图来描述全局拓扑关系,然后利用广义水平集实现拓扑层最优路径规划,最后在栅格层利用快速行进法(fast marching method,FMM)实现路径再规划。该方法平衡了单一路径规划算法的缺陷,发挥了融合算法优势,但未充分考虑机器人运动特性,生成的路径较长且拐点较多。MARTINS等[19]提出一种IMOA-star(improved multi-objective a-star)方法,通过重复利用存储为pickle格式的障碍图,避免了频繁计算栅格的启发函数从而缩短算法的执行时间,同时引入路径问题感知执行器,减小了路径长度和提高了路径平滑度,然而该方法未充分考虑动态障碍物对障碍图更新的影响。徐开放[20]提出一种基于度量-拓扑分层结构的复合地图的D*Lite和BP神经网络融合路径规划方法,全局采用低分辨率地图,并使用D*Lite算法规划出一组路径节点序列,路径节点间利用增强学习实现了相邻两个节点的抵达问题。该方法将任务拆解,减少搜索空间,是一种较好的解决方案,但只能输出离散的动作,不利于机器人连续控制。深度强化学习(deep reinforcement learning,DRL)兼具深度学习的感知能力和强化学习的决策能力,有望改善现有路径规划方法在未知环境下的缺陷,这类端到端的方法能够对周围环境迅速作出决策,灵活性高、适应能力强,可以更好地处理突发情况。然而,DRL还有些亟待优化的问题,如训练耗时长、样本利用率低等问题。
为了克服上述方法的不足且更好适应部分未知的复杂大场景环境,本文提出一种面向复合地图的移动机器人分层路径规划方法,引入层次图思想,建立了拓扑-栅格-度量复合地图,实现了不同抽象程度和精细程度的环境表示。在此基础上进行路径规划,先针对拓扑-栅格地图生成全局优化的初始路径,机器人沿初始路径行驶时再探测周围局部环境,并使用深度强化学习算法进行避障路径规划,通过分层分区域方式提高路径规划算法的效率和成功率。
1 复合地图分层路径规划框架
1.1 复合地图描述
1.1.1层次图定义
目前多数路径规划方法均基于某种环境地图在全局范围内开展搜索,搜索范围大导致搜索效率不尽人意。为减小路径规划算法的搜索范围,通常会对大规模场景进行抽象描述和层次分解,层次图非常适合这种情况。
层次图采用多叉树来表达,树中包含多个抽象层次,抽象程度自上而下逐层降低。每一层由一个或多个关键节点构成,节点之间通过边连接,因此每个抽象层都是一幅图。构建层次图是一个迭代的过程,某一层中的关键节点是其下一层图的抽象描述,逐层分解直至对环境做出详细的描述。每个关键节点都代表了某一局部环境,故层次图不宜过深,否则导致关键点间隔过近,抽象程度降低,进而会增加算法的复杂度。层次图序列L可表示为
L={L0,L1,L2,…,Ld}
其中,Li为第i层抽象。值得注意的是,L0为根层次,是对环境地图的最高层抽象;Ld为最深层,即最小的子地图。层次图中每一层Li都有图Gi对应,Gi由关键节点、普通节点、连接各节点的边及其权重等信息组成,本文将其演化为拓扑地图。普通节点仅用于辅助路径搜索,而关键节点负责连接子地图与其父地图,在层次图的同一层次中通过离线先验路径连接相邻子地图。以制造业公司场景为例,为每个子区域设置关键节点,层次图的表达方式如图1所示。

图1 层次图示例Fig.1 Example of hierarchical graph
在图1中,红色方点和蓝色圆点分别代表关键节点和普通节点,连接节点的黑色线条为先验路径(边)。其中,两个带有五角星标记的关键节点是同一个点,只不过显示在不同层级上,可实现相邻层级间的访问。根层次L0描述了公司的组织架构,包含行政室、研发室、制造室和休息室,L1则进一步描述制造室的功能布局。
1.1.2复合地图架构
首先,通过机器人操作系统(robot operating system,ROS)软件gmapping功能包将移动机器人作业环境描述为栅格地图形式。然后,利用层次图将全局栅格地图划分为若干个不同层次的子地图,且每个子地图均设置关键节点,同一层次的关键节点间通过离线路径(边)连接,具有明显拓扑特征,进而构建拓扑地图。栅格地图中,某物体的坐标通常由它占据栅格的中心点坐标替代,这种表示方式的精度有限,因此,移动机器人在运行过程中利用激光雷达和惯导系统等传感器维护局部度量地图,实现更高精度的位置表示。由此建立了一种拓扑-栅格-度量复合地图,如图2所示。
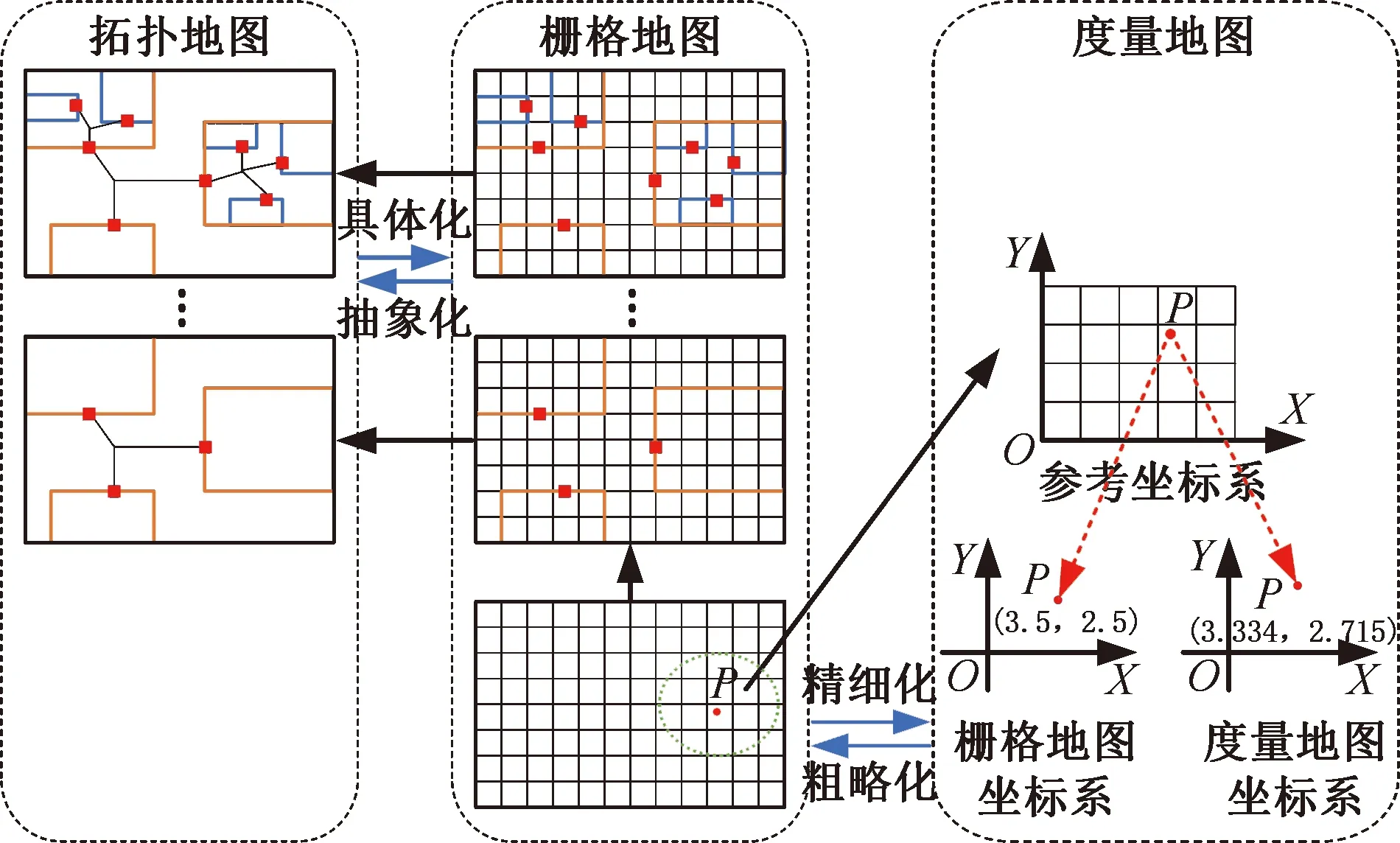
图2 拓扑-栅格-度量复合地图Fig.2 Hybrid topological-grid-metric map
图3展示了面向复合地图的分层路径规划架构。拓扑地图反映了关键节点之间的空间位置关系,利用Floyd算法规划最优点集序列,确保起点所在子地图的关键节点到终点所在子地图的关键节点之间的区间路径是离线最优的。将关键节点代表的子地图内部展开为栅格地图,提出改进A*算法进行内部路径的局部规划。度量地图利于移动机器人精细化描述周围环境,提出改进深度确定性策略梯度(deep deterministic policy gradient, DDPG)算法进行机器人的避障规划。

图3 面向复合地图的分层路径规划架构Fig.3 Hierarchical path planning architecture forhybrid map
1.2 分层路径规划方案
分层路径规划方案的流程如图4所示,主要分为两个步骤:首先在拓扑-栅格地图上规划出一条全局优化初始路径;然后移动机器人沿初始路径在行驶过程中实时检测其周围环境并维护局部度量地图,若离机器人最近障碍物距离小于避障阈值,则运行针对度量地图的改进DDPG算法进行避障路径规划。

图4 复合地图分层路径规划流程Fig.4 Procedure of hierarchical path planning forhybrid map
分层路径规划的处理流程如下:
(1)在栅格地图上采用细化算法生成离线先验路径,提取拓扑特征完毕后,构造拓扑地图并完善层次图。
(2)判断起始栅格S和目标栅格D是否处于同一子地图中,即判断是否隶属于层次图的同一节点,若是则直接利用改进A*算法规划出S到D的优化路径即为全局优化初始路径,转至步骤(6);否则转至步骤(3)。
(3)分别获取S和D在层次图中的深度LS、LD及它们所在子地图的关键节点CS、CD,若LS (4)以S为起点,CS为终点,利用改进A*算法在S所在子区域的栅格地图上搜索出一条局部路径并保存。同理,将CD设为起点,D设为终点,规划出另一条局部路径并保存。若无法搜索出可行解,则路径规划失败,算法结束。 (5)将步骤(3)生成的起始关键节点和目标关键节点之间的离线先验路径和步骤(4)搜索到的S和D所在子地图的局部路径合并,得到全局优化初始路径。 (6)机器人沿着初始路径行进时,一旦机器人离最近障碍物的距离小于避障阈值,利用改进DDPG算法完成避障后重新回到初始路径;直到机器人到达目标位置D,算法终止。 拓扑地图不易构建,原因在于拓扑特征(节点)的定义和识别难度较大。本节将利用细化算法生成离线先验路径,以选取拓扑特征,构建拓扑地图。在此基础上还研究了离线路径点集序列的优化方法,最终生成最优先验路径。 2.1.1离线先验路径生成 细化算法[21]是图像处理中常用的方法,能够有效提取原图像形状的拓扑结构。二维栅格地图由“0”和“1”组成,可以视为一幅二值化图像,通过细化算法将自由栅格区域细化,最终生成安全路径。需要注意的是,细化算法处理的是值为1的像素,故处理时需把自由栅格视为“1”,障碍栅格视为“0”。 细化算法的主要思想是:检查图像中某一像素是否符合删除的条件,一旦满足立即删除该像素(像素值由1变为0),重复迭代上述过程直到无法继续删除为止。检查像素p1时建立图5所示的3×3窗口,将p1作为中心单元,并判断周围的8邻域是否满足细化条件。每次迭代分为如下两个步骤: (1)2≤B(p1)≤6;A(p1)=1;p2×p4×p6=0;p4×p6×p8=0; (2)2≤B(p1)≤6;A(p1)=1;p2×p4×p8=0;p2×p6×p8=0。 其中,B(p1)表示p1周围8邻域中数值为1的个数;A(p1)表示以顺时针方向统计p2,p3,p4,…,p8,p9,p2数值从0变为1的次数。步骤(1)和步骤(2)交替进行,只有步骤(1)或步骤(2)中所有条件同时满足,p1才能被删除。 图5 细化算法窗口Fig.5 Window of thinning algorithm 2.1.2拓扑特征提取 栅格地图经过细化算法后会生成较为简洁的离线先验路径,该路径存在明显拓扑特征,利于构建拓扑地图。首先,人工选取区域入口栅格或其他具有代表性的栅格作为子地图的关键节点;其次,提取路径的分岔点作为拓扑图中的普通节点;最后,统计连接相邻节点的边所占据的栅格数作为边的权。每个节点存储自身编号和所有与之相连的节点编号及该拓扑边的权重,拓扑特征提取完毕后构建各层次对应的拓扑地图。 图6 拓扑特征提取示例Fig.6 Example of topological feature extraction 图6展示了按以上规则提取出来的拓扑特征,图中黑色栅格为障碍物,白色栅格为自由空间,灰色栅格为细化算法生成的离线先验路径,红色方形为关键节点,蓝色圆点为普通节点。 2.1.3优化离线路径点集序列 拓扑地图包含关键节点、普通节点和连接节点的边,是一张带权的路径网络图,从起始节点出发可以有多条路径到达目标节点。机器人路径规划期望路径长度尽可能地短,因此拓扑地图上的路径规划问题等价于在带权图中寻找起点到终点的最优点集序列问题。本文选用Floyd算法在带权图中求取多源点之间的最短距离。由于Floyd算法作用于拓扑地图,而拓扑地图又是对环境的高度抽象,局部细微的变动对拓扑结构影响不大,因此真实环境的细微变化不必在拓扑地图上频繁调用Floyd算法。 A*算法通过包含启发信息的代价函数来搜索最优路径,代价函数f(n)由两部分组成:起点沿着已生成的路径到达当前节点的开销g(n)和当前节点到终点的预估开销h(n),可表示为 f(n)=g(n)+h(n) (1) A*算法建立并维护两个列表:存放已经探测到但还未访问节点的Open列表和存放已经访问过节点的Close列表。初始化时只包含起点,Close初始化为空。从起点开始,遍历周围8邻域节点,若该节点在Open表中不存在,则加入至Open,否则判断是否需要更新Open表中该节点的代价。然后从Open表中弹出代价值最小的节点,同时移入Close表,以该节点为路径当前节点继续向目标点拓展,重复以上过程直至Open表为空或搜索到终点。路径上每个节点都有一个指向父节点的指针,通过跟踪指针向前回溯即可找到最佳路径。 标准A*算法在扩展节点时比较盲目,可能将多余节点加入Open表,增加了维护Open表代价的同时扩大了搜索空间,导致算法在大范围空间下的搜索效率不够理想。此外,规划出来的路径拐点较多,不利于移动机器人跟踪。针对以上问题,对A*算法进行改进,如图7所示。本文采用双向搜索机制,同时开展从起点向终点的正向搜索和从终点向起点的反向搜索,逐步生成路径节点向中间靠拢;在扩展过程中依据方向信息对候选的节点进行筛选,过滤掉一些无效节点,提高搜索效率;最后对生成的路径进行修饰,删除冗余点,提高路径质量。 图7 改进A*流程图Fig.7 Flow chart of improved A* algorithm 2.2.1筛选扩展点 图8展示了A*算法扩展过程,其中S为起始位置,m为被扩展到的节点,D为目标位置。路径规划期望路径长度尽可能地短,即路径方向尽可能贴合起点指向终点的方向SD。θ为当前节点到终点的方向mD与期望方向SD的角度偏差,可表示为 (2) |θ|越小,节点m被加入Open表的可能性越大。 图8 A*算法扩展过程Fig.8 Extension process of A* algorithm 式(2)中涉及反三角函数运算,在实际运用过程中会占用较多算力。为了简化扩展节点和预期路径符合程度的表示,同时放大各扩展节点之间的这种差异,本文选用图8中绿色矩形面积来引导路径规划过程。以m为原点分别向标准坐标系的X轴和Y轴延伸,并与边SD、DT相交于两点,可构成一个矩形,矩形面积φ(m)可表示为 (3) φ(m)越小,当前被扩展到的节点和预期路径符合程度越高,越有机会加入Open表中继续扩展。设置面积阈值φ0,当φ(m)>φ0且满足p(m)>p0时(其中p(m)为随机概率,p0为信任阈值概率),忽略当前被扩展的点m,重新选择新的扩展点。其余情况对m的处理方式和标准A*算法保持一致。通过引入方向指引信息,有一定概率忽略方向性不强的节点,进而减少了Open表中候选点的个数,缩小了算法的搜索空间。 2.2.2剔除冗余点 虽然上述改进步骤能够有效规划出一条路径,但依旧遵从8邻域扩展,即以45°为分辨率选择下个栅格,该方式生成路径会存在较多拐点,且并不一定是最优路径,故改进路径生成策略。首先在前文获得的初始路径中每对相邻节点距离二等分处插入新节点。然后将所有节点按起点指向终点方向从小到大编号,从终点向前搜索是否有可以略过的冗余点。当两节点连线经过障碍物时,则说明编号小的节点无法被删除,否则即可删除。重复以上过程直到搜索到起点,最后按顺序连接剩余的节点,如图9所示,其中虚线即删除冗余点后的路径。 图9 删除冗余点后的路径Fig.9 Path after removing redundant points 当移动机器人沿全局优化初始路径运行时,针对部分未知场景中的动态障碍物,研究了基于深度强化学习的避障路径规划方法,其研究方案如图10所示。移动机器人负责将自身感知到的状态数据输送至Actor网络中,经过基于价值分类经验回放机制的深度确定性策略梯度(deep deterministic policy gradient based on value-classified experience replay, VCER-DDPG)算法决策后,控制器输出信号指导机器人做出相应动作。 图10 基于VCER-DDPG算法的局部路径规划框架Fig.10 Local path planning framework based on VCER-DDPG algorithm VCER-DDPG算法的核心由两部分组成:价值分类经验回放池和Actor-Critic网络架构。价值经验回放池主要负责存储训练过程中产生的经验样本,并按一定的采样策略抽取部分样本用于训练。Actor称为策略网络,完成状态空间到动作空间的映射;Critic称为价值网络,使用价值函数对Actor输出的动作进行评价,指导Actor改进策略。为降低损失函数震荡发散概率,提高算法的稳定性,Actor和Critic均采用双重神经网络架构,即在线网络(online)和目标网络(target)。VCER-DDPG算法共包含4个深层神经网络,即 (4) (5) 其中,μ、μ′分别为online动作策略函数和target动作策略函数;θμ、θμ′分别为online Actor和target Actor网络参数;Q、Q′分别为online价值函数和target价值函数,θQ、θQ′分别为online Critic和target Critic网络参数;S为状态,时间步为t时的状态表示为St。VCER-DDPG训练的本质是利用深度学习更新优化Actor和Critic的网络参数,最终获得能应对复杂避障问题的online Actor网络。 完整的局部路径规划过程如下:首先,激光雷达的距离点云数据、机器人当前位姿、目标位姿被合并成一维状态数组St,在线策略网络依据状态St生成动作μ(St),叠加行为策略β后得到机器人最终执行的动作at。动作at由线速度和角速度组成,机器人控制器将at转化为实际控制信号,执行完毕后到达新的状态St+1。环境判断当前回合是否结束,同时利用奖励函数对动作at进行评价,给出奖励值rt。这一过程产生的经验样本(St,at,rt,St+1,done)由价值分类经验回放池进行存储。模型训练时,根据分层采样策略从经验回放池抽取小批量样本送入Actor和Critic网络进行训练,重复上述过程直到模型网络收敛至最佳避障策略。 原始经验回放机制采用等概率采样,未区分经验样本的价值,重复学习简单样本对网络指导效率有限,网络收敛速度较缓慢,因此,在训练过程中根据样本价值,将经验样本分类存放至不同的子经验回放池中。制定合适的样本价值衡量标准是对经验样本进行分类的前提,大多数强化学习算法采用时间差分误差δ作为状态值函数的估计,|δ|越大,向预期动作值的校正就越积极,因此δ很大程度上与样本的学习价值相关联。十分成功和失败的经验样本通常拥有较高的|δ|,重复回放这类样本能够及时审视当前策略的学习效果,加快网络收敛,提高训练效率。然而训练初期,对环境的探索有限,策略还未成熟,在状态空间的边缘也可能出现较大的|δ|,可能改变网络的收敛方向,仅仅依据时间差分误差δ无法准确衡量样本价值。从短期来看,奖励值r直接表现了动作的好坏程度,高奖励值样本在训练初期具有学习价值。本文将时间差分误差δ和奖励值r结合起来,制定了价值衡量方法,其表达式为 Vj=α|rj|+(1-α)|δj| (6) δj=rj+γQ′(Sj+1,aj+1;θQ′)-Q(Sj,aj;θQ) (7) 其中,Vj为样本j的价值,|rj|为样本j的奖励值的绝对值,γ∈(0,1]为奖励值折扣因子,α为|rj|的权重,|δj|为样本j的时间差分误差的绝对值,(1-α)为|δj|的权重,α随着训练过程动态更新。训练初期α取1,主要利用奖励值引导智能体快速学习策略,随着训练深入,时间差分误差δ能更好地指导策略更新,α逐渐减小以提高δ的权重。 价值分类经验回放池的结构如图11所示,分别由存放高价值样本的子回放池B1、存放近期样本的子回放池B2、存放普通样本的子回放池B3组成。子回放池均采用队列作为存储容器,新样本从队尾插入,容量达到上限时从队头弹出样本。 图11 价值分类经验回放池结构Fig.11 Structure of value-classified experience replay pool 价值分类经验回放池的构建步骤为:初始化时设置B1、B3两个子回放池中所有样本价值的平均值Vm为0,同时将奖励值的权重系数α设为1,训练过程中每产生一条样本先加入B2队尾,若B2达容量上限则从队头弹出一个样本,并计算该样本的价值,若高于Vm则将该样本添加至B1,反之存入B3。存储完毕后,更新Vm和α,重复以上过程直至训练结束。 为了保证采样所得样本的时效性和多样性,本文设计了分层采样策略,分别从B1、B2、B3子回放池中随机抽取适量样本。记小批量采样总数为N,包括子回放池B1采样数N1、子回放池B2采样数N2、子回放池B3采样数N3,即 N=N1+N2+N3 (8) 其中,N2为固定值,确保每次小批量采样均有近期样本,该类样本具有时效性,有助于及时调整网络收敛方向。训练初期,N1取较大值,通过选取大量高质量样本来促进网络朝正确方向收敛。随着训练推进,策略网络的成熟,机器人表现越发优异,高价值样本出现频率越来越高,为避免过拟合,应适当降低N1、提高N3。 VCER-DDPG的算法伪代码如下: 为了验证本文所提方法的有效性,将采用计算机软件仿真与机器人样机实验相结合的手段,分别在C++开发环境下进行全局路径规划仿真实验;然后在Gazebo仿真引擎中验证所提局部路径规划算法的避障性能;最后在真实场景中验证本文所提复合地图分层路径规划方法的有效性。 本次实验的环境由100×100个网格组成,每个网格边长为10像素,黑色栅格为障碍物,白色栅格可自由通行。实验选择标准A*算法、蚁群算法作为对比算法,以验证拓扑-栅格地图分层路径规划方法的性能,实验参数设置如表1所示。 表1 全局路径规划仿真实验参数 每种方法分别进行了3次路径规划任务,图12所示为采用标准A*算法进行路径规划的结果,图13所示为由蚁群算法规划获得的路径,图14所示为本文分层规划方法生成的路径。图12~图14中红色线条是算法生成的最终路径,灰色部分为初始路径或离线路径,算法搜索过的栅格(可反映规划算法的计算量)会被标记为绿色。 从图12、图13中可以看出,标准A*算法和蚁群算法生成的路径安全性不高,部分路段长距离贴合障碍物,机器人沿路径行走时较易发生碰撞。此外,算法在搜索过程中缺少方向性引导,搜索空间较大,路径摆动较为明显,不利于机器人运动控制。由图14可知,基于拓扑-栅格地图的分层路径规划方法利用细化算法可生成安全度较高的离线先验路径,同时在子地图内部运用改进A*算法时,对目标点的搜索更具有方向性,路径拐点更少,利于机器人控制。 (a)任务1 (b)任务2 (c)任务3图12 标准A*算法生成路径Fig.12 Path generated by the original A* algorithm (a)任务1 (b)任务2 (c)任务3图13 蚁群算法生成路径Fig.13 Path generated by the ACO algorithm (a)任务1 (b)任务2 (c)任务3图14 分层路径规划算法生成路径Fig.14 Path generated by the hierarchical path planning algorithm 为了通过量化性能指标对比分析三种路径规划方法的性能,对上述实验过程的路径长度、危险栅格数(经过障碍栅格周围8邻域)、搜索栅格数、运行时间进行统计,实验数据如表2所示。从表2中数据可知,相比标准A*算法,拓扑-栅格分层路径规划方法的路径长度平均增大了4.89%,但危险栅格数减少了42.99%,搜索栅格数减少了80.20%,运行时间缩短了91.75%;相比蚁群算法,拓扑-栅格分层路径规划方法的路径长度平均增大了11.1%,但危险栅格数减少了50.5%,搜索栅格数减少了84.8%,运行时间减少了4个数量级。综合以上实验数据可以发现,本文所提的拓扑-栅格分层路径规划方法显著缩小了算法的搜索空间,极大提高了搜索效率,最终生成的路径兼具安全性和平滑度,能够有效解决复杂大场景环境下的路径规划问题。 表2 全局路径规划实验数据 为了验证VCER-DDPG避障路径规划方法的有效性,首先结合ROS软件和TensorFlow框架进行DDPG深度学习程序的开发,并根据表3中的参数进行训练,训练完毕后,可通过加载模型网络参数以应用最终习得的避障策略。然后,在Gazebo软件中设计一个混合障碍场景:方形立柱充当静态障碍物,圆柱体以0.4 rad/s速度逆时针旋转充当动态障碍物。移动机器人在该场景中依次到达5个指定目标点记作成功,否则记为失败。 表3 训练超参数 实验过程中,使用了较为成熟的move_base导航功能包作为对比算法,分别对采用VCER-DDPG算法和move_base算法的机器人进行15次测试,统计成功率、路径长度、行驶时间等性能指标(其中路径长度和行驶时间只统计导航成功的测试数据)。两种方法的机器人运行轨迹如图15所示,实验数据如表4所示。 (a)VCER-DDPG的轨迹 (b) move_base的轨迹图15 动态避障的仿真轨迹Fig.15 Simulation trajectories of dynamicobstacle avoidance 表4 动态避障的实验数据 由实验结果可见,move_base功能包由全局路径规划器A*算法和局部路径规划器DWA算法构成,不易陷入局部最优,故move_base方法规划的路径长度更短。然而,复杂的决策机制同时可能会导致短期无可行解时机器人在原地等待,直至出现可行解。该行为也导致平均行驶时间稍长,甚至路径规划失败。而本文所提的深度强化学习算法是端到端的方法,根据状态直接输出动作,决策迅速,面对障碍主动进行避障,虽然牺牲了一些路径长度性能,但具有较高实时性且避障成功率更高,更适应动态未知环境。 真实场景实验中采用的移动机器人平台如图16所示。该机器人采用差速驱动方式,前面有两个主动轮,后面两个万向轮作为从动轮,并安装有多种进行环境/机器人状态感知的传感器,包括用于建图和定位的倍加福R2000激光雷达、用于探测周围障碍物的RPLIDARA2激光雷达、加速度计、陀螺仪模块等。 图16 移动机器人平台Fig.16 Mobile robot platform 为了模拟大范围的工作空间,本次实验由一个400 m2的实验室和50 m长的走廊及若干个房间组成,实验环境如图17所示。R2000激光雷达安装高度为60 cm,部分物体未被扫描到,建图时无法获取这些物体信息,对全局路径规划可能产生一定影响。然而,RPLIDARA2激光雷达的安装高度为46 cm,能够保证扫描到大多数障碍物,机器人运行过程中将建图时未能探测的物体视为障碍物从而采取避障策略。 (a)实验室 机器人平台基于ROS开发,具体步骤如下:首先配置系统环境,包括搭建分布式通信网络,利用SSH协议从远程端登录机器人主机,运行rviz工具;然后运用gmapping功能包建立整体环境的栅格地图,为后期定位和路径规划做准备;再者利用ROS插件机制,将move_base框架中的全局和局部路径规划器分别替换为本文所提的拓扑-栅格路径规划方法和VCER-DDPG局部路径规划方法;最后机器人运行基于move_base和amcl的导航算法,并通过笔记本上的rviz工具选取目标点,进行导航实验。 本次导航实验的运行轨迹如图18所示,其中红色圆圈处是机器人所处的初始位置,绿色箭头的末端是目标位置,机器人导航过程中的实际运行轨迹如图中的蓝色线条所示。在实验室和房间的门口设置关键节点,在它们内部主要由改进A*算法生成局部路径,在保证安全的前提下以路径最短为优化目标,因此路径相对径直。而走廊用于连接实验室和房间,机器人由离线路径引导,故轨迹更靠近区域中心。由图18可知,机器人绝大多数时间都沿着全局优化初始路径运行,当激光雷达探测到建图时未扫描到的障碍物或突然出现的障碍物时会自主进行局部路径规划。 图18 导航实验Fig.18 Navigation experiment 以图18中橙色线段分析主要的避障过程,图19通过时间序号的形式展现了各时刻机器人和行人的位置。面向卫生间走动的行人和长方体纸箱分别充当动态和静态的障碍物。记最近障碍物相对机器人前进方向的角度为ao,位于左侧的障碍物ao∈[-60°,0),位于右侧的障碍物ao∈(0,60°];记最近障碍物相对机器人的距离为do。这两个指标作为状态空间的组成部分,很大程度上影响了机器人的避障策略,故表5列举了不同时刻下的ao和do,并结合线速度v和角速度ω的变化情况(图20)来分析避障过程。 图19 避障过程Fig.19 Obstacle avoidance process 由图20可以看出,开始时,机器人沿初始路径向前行驶,在t=1.7 s时,探测到右前方行人,为避免发生碰撞,角速度迅速调整为负值,向左前方避障;t=3 s时,行人位于机器人右前方0.56 m处,由于距离较近,随即减小线速度,等待行人通过;t=4 s左右,行人位于机器人左前方,且已穿过走廊大半,基本不再产生干扰,机器人提高线速度的同时降低角速度幅值,并减小左拐的幅度;t=5.4 s时,纸箱成为主要避障目标,角速度变为正值,向右侧避障;t=9 s时,机器人即将绕过纸箱,同时位于走廊中间,角速度稳定在0附近,径直向前行驶。避障完成,回到初始路径上,最终安全、准确地到达目标点。 表5 避障路段的实验数据 图20 避障线速度和角速度Fig.20 Linear velocity and angular velocity duringobstacle avoidance 真实场景下的移动机器人路径规划实验结果表明,本文所提的复合地图分层路径规划方法在实际场景应用中也具有较好的效果。 针对部分未知复杂大场景环境,提出一种基于拓扑-栅格-度量复合地图的移动机器人分层路径规划方法。首先采用层次图思想,将机器人作业环境划分为多个以栅格表示的子地图,并建立多个子地图的拓扑架构及局部区域的精细化描述模型。其次,在不同地图层级上分区域搜索机器人路径,在拓扑地图上采用Floyd算法规划子区域之间的区间路径,面向栅格地图提出搜索子区域内部路径的改进A*算法,针对动态障碍物在度量地图上提出VCER-DDPG避障路径规划方法。最后,采用计算机软件仿真与机器人样机实验相结合的手段,验证了所提分层路径规划方法的有效性,路径搜索效率和避障成功率有明显提高,生成的路径兼具安全性和平滑性。2 拓扑-栅格分层全局路径规划
2.1 拓扑地图最优先验离线路径规划

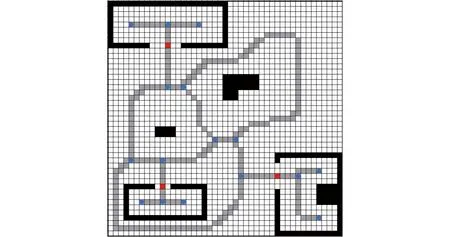
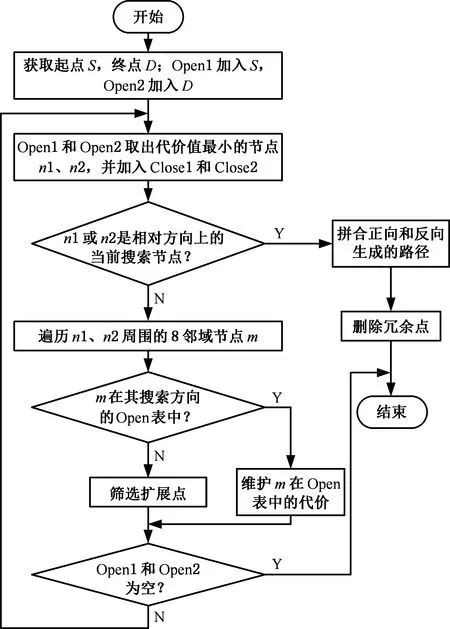
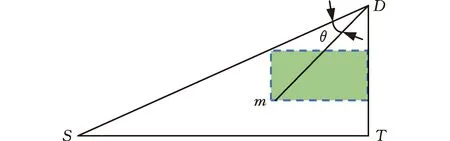
2.2 基于栅格地图的改进A*算法
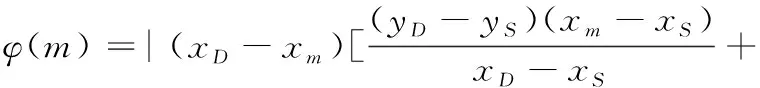

3 度量地图局部路径规划

3.1 价值分类经验回放池

3.2 VCER-DDPG算法流程

4 实验分析
4.1 全局路径规划仿真实验
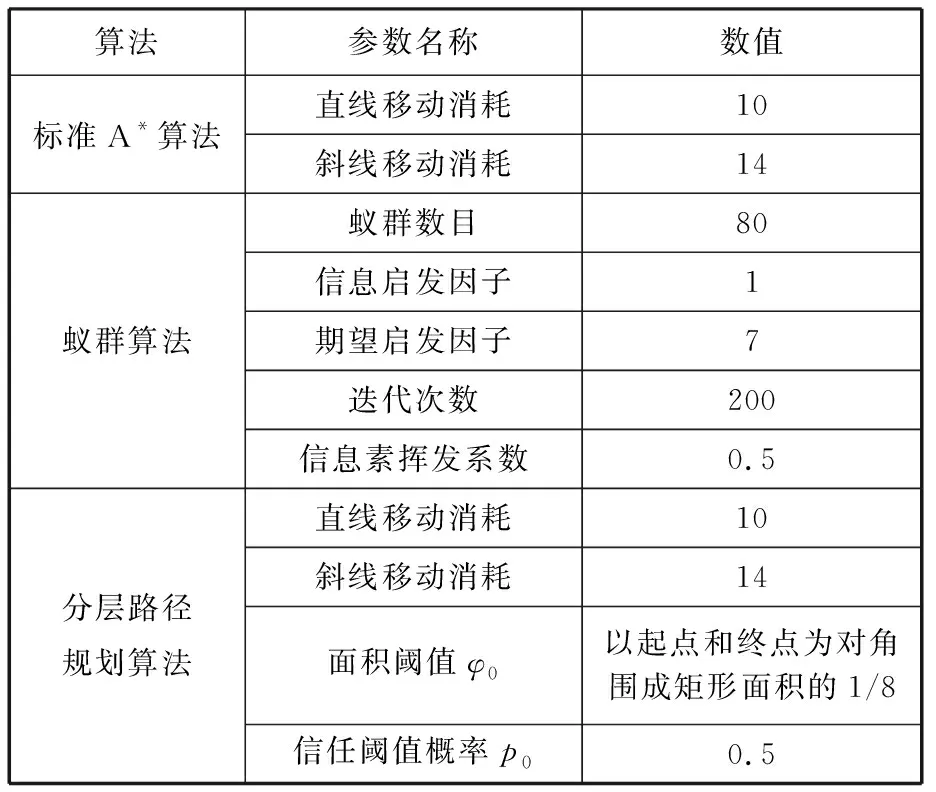
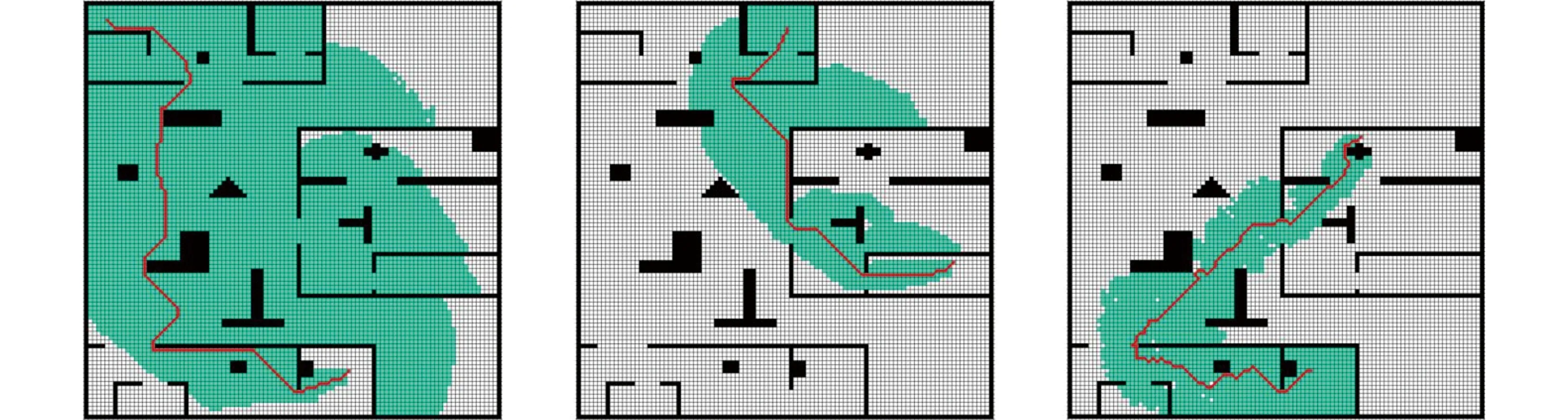

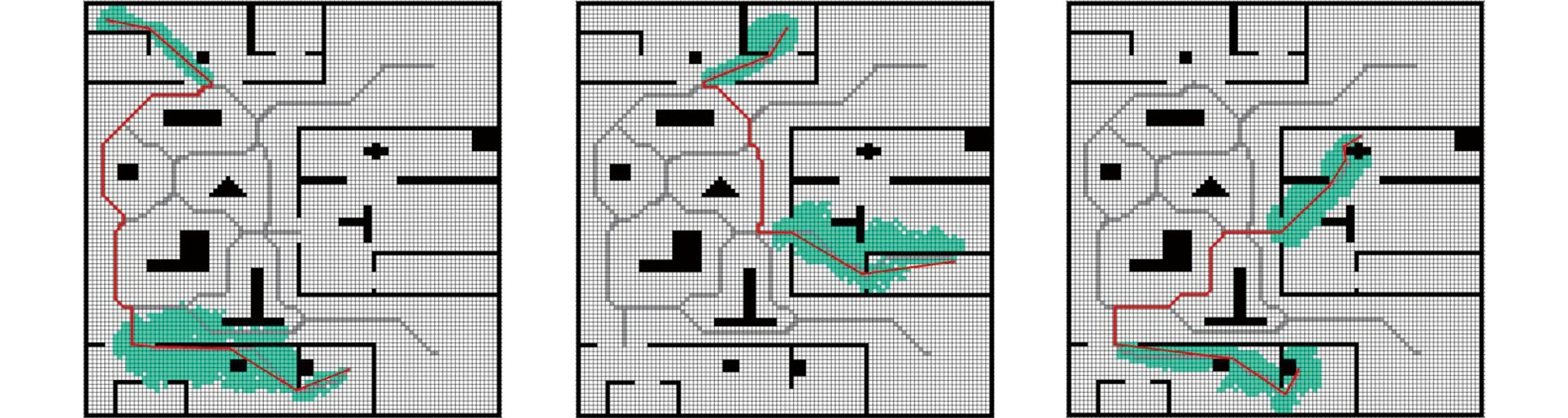
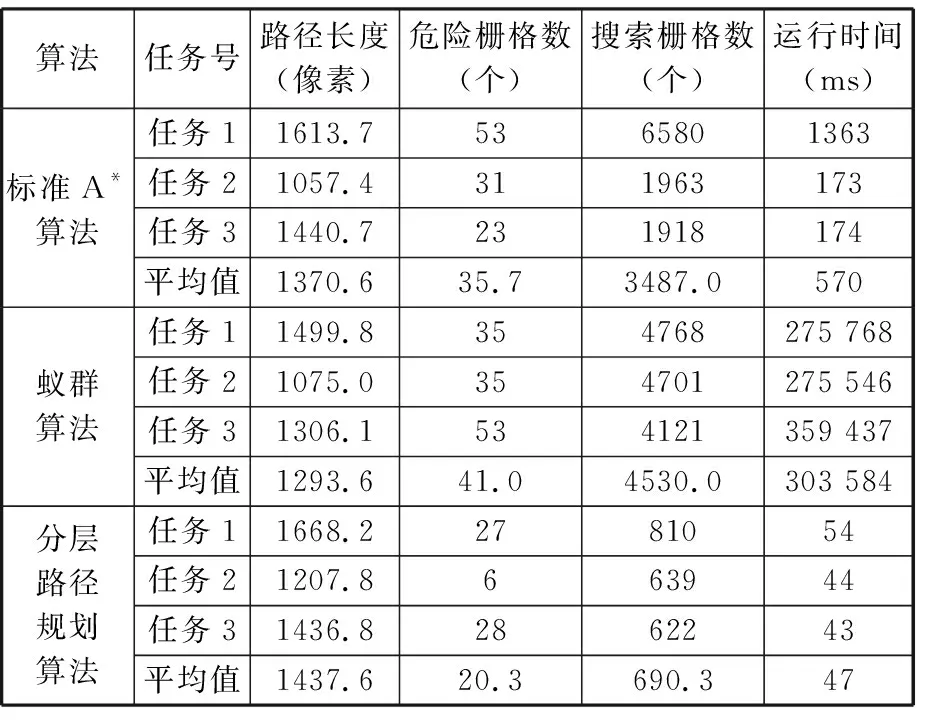
4.2 避障仿真实验
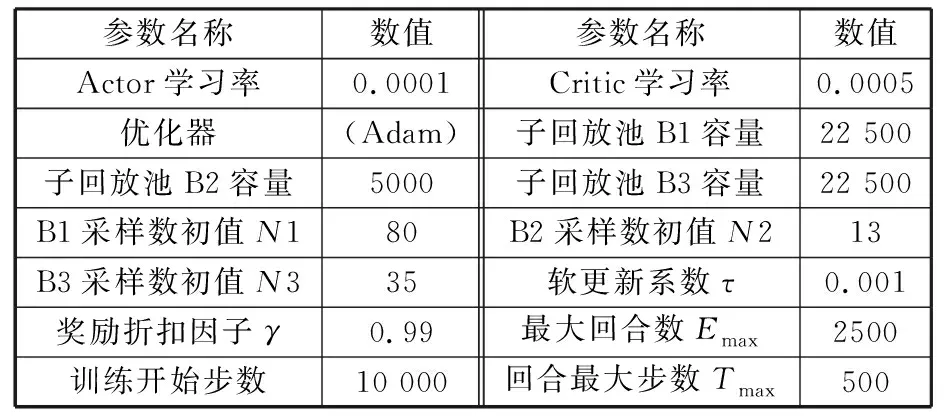
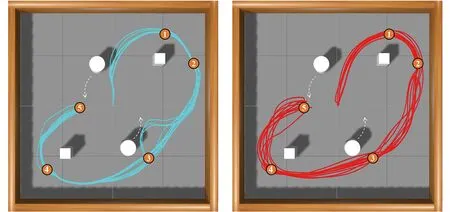

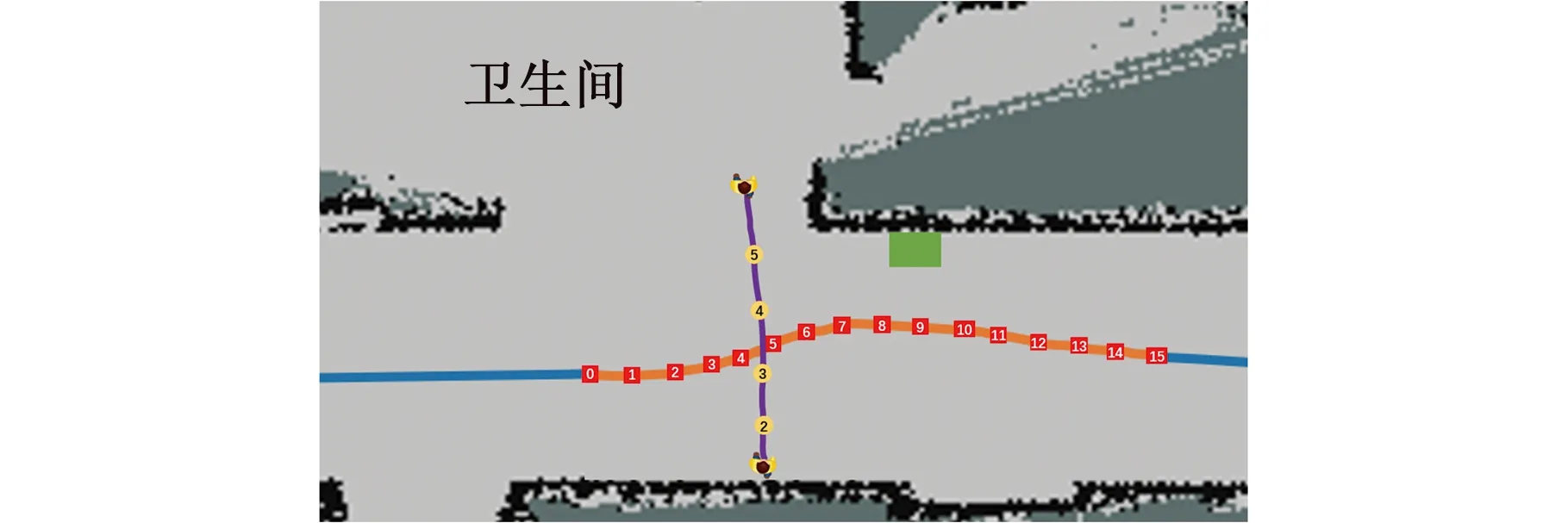
4.3 复合地图分层路径规划实验


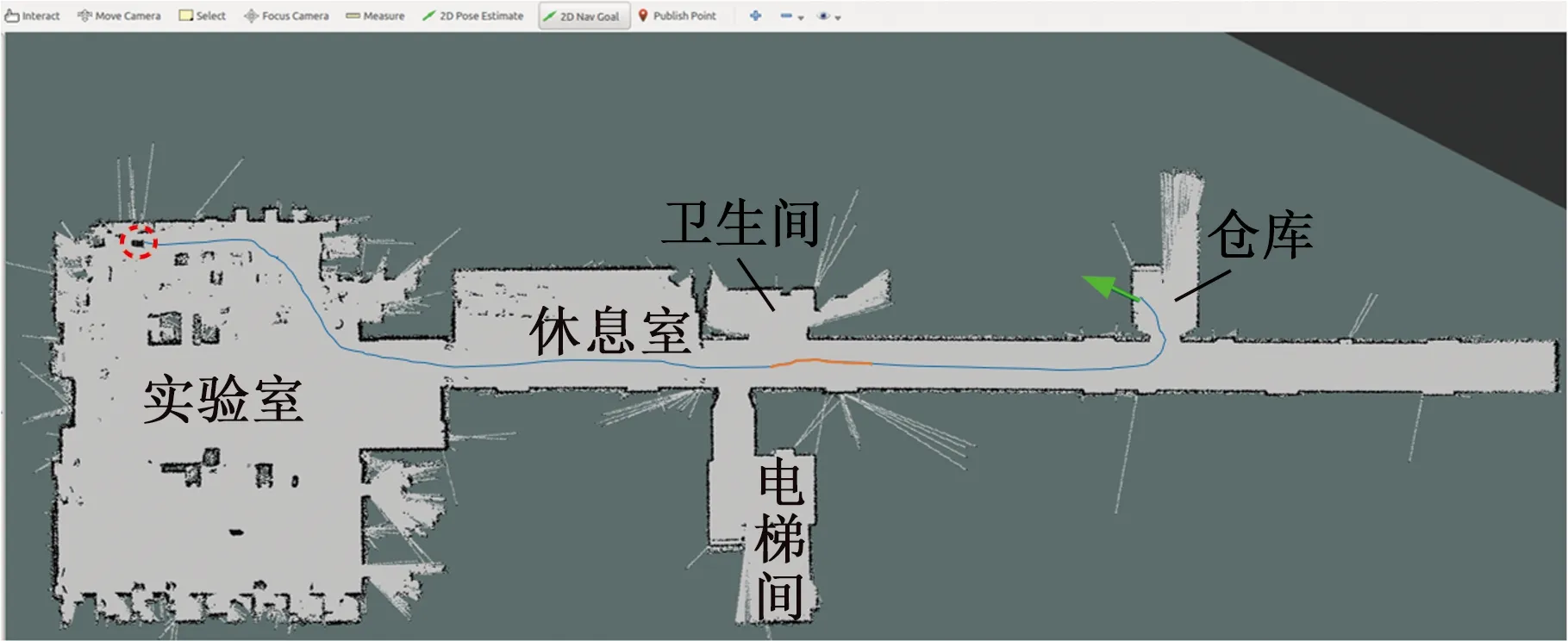


5 结语

