基于γ散度的单元水平模型小域稳健估计
庞智强,王朝旭,2,牛玺娟,2
(1.兰州财经大学 统计学院,甘肃 兰州 730020;2.青海师范大学 数学与统计学院,青海 西宁 810008)
一、引言
在抽样估计领域,由于受到小样本乃至无样本的挑战,小域估计方法得到了学者们的一致青睐。相比于传统的直接估计方法,借助于辅助变量的小域估计方法能够更好地解决小样本和无样本问题。实践中,小域估计方法在政府统计、人口统计、医学统计、农业统计、贫困率估计等领域有广泛的应用[1-7]。在理论层面,小域估计也受到高度重视,从Fay提出区域水平的Fay-Herriot(FH)模型[1]、Battese等提出单元水平的误差嵌套(NER)模型[2]、Datta和Ghosh提出的小域估计的贝叶斯预测方法[3],到Rao和Molina关于小域估计基础理论的系统综述[4]、Morales等提出的几类混合模型小区域估计理论[5],小域估计已经形成了较为完整的理论体系。在抽样调查的范畴,小域估计方法也是解决多层次目标量估计的有效途径之一,金勇进和赵雪慧对此曾做过专门讨论[8]。
在小域估计方法方面,基于模型的小域估计方法受到学者们更多的关注。基于模型的方法不仅能够估计无样本区域中感兴趣的变量值,还能更好地拟合观测数据的结构使估计具有更小的偏差。作为小域估计的基础模型之一,单元水平模型能够处理小域中每个单元级别的目标变量估计,并且能通过单元数据计算相应的区域水平值。受限于数据的收集、辅助变量的获取以及模型计算等方面的限制,单元水平模型并不像区域水平模型那样受学者的关注。若能够获取单元级别的观测数据和辅助信息,则建立单元水平模型是小域估计中更好的选择。如Battese等利用误差嵌套(NER)模型结合抽样数据和卫星数据估计县级水平农作物面积[2]。Datta和Ghosh推广了NER模型,利用分层贝叶斯方法讨论了广义线性混合模型下的估计量[3]。在小域模型参数以及目标变量的估计方面,经验最佳线性无偏估计量(EBLUP)成为应用最为广泛的方法,该方法能够很好地解决混合线性模型的估计问题。当观测变量为二分变量或计数变量时,经验贝叶斯(EB)方法受到了更广泛的应用[4]。在传统的单元水平模型中,区域随机效应和模型随机效应部分的误差均假定服从正态分布,但在实际应用中,观测数据中离群值很常见,使用传统的EBLUP方法会产生较大的估计偏差。本文重点关注随机效应分布非正态及模型观测存在离群值的单元水平模型,并提出针对这种模型的稳健估计方法。
离群观测是任何调查中都不可避免的事实[9],因离群值普遍存在,且会对估计量产生较大影响,因此众多研究专门探讨减小离群观测对调查估计影响的方法,常见的有三种。第一种,删除离群观测值,用剩余观测值进行估计和预测。很显然,这一方法当样本量非常大时,删除少数的离群观测可能是可行的。但当样本量本来就比较小时,这种方法不仅会带来信息的丢失,同时还会导致估计量偏离真实值。第二种,用非离群观测值替代离群观测值进行估计,并在非抽样总体中采用稳健投影的方式进行稳健预测。然而正如Chambers等所言,若观测值是准确获取的,不能认为每个观测值是唯一的,且没有理由说明在未抽样总体中不包含离群观测值[9]。第三种,通过构建对于离群观测值不敏感的稳健估计量,来减小离群值对估计结果影响,这类方法也是学者们关注的主要方法,本文也采用了这类稳健估计方法。
有关小域稳健估计的研究最早见于Ghosh和Lahiri的成果,他们利用贝叶斯方法讨论了分层均值的稳健估计[10]。后来,分层贝叶斯方法[3]、长尾分布假设、分位数回归等方法均用于研究稳健小域估计问题,但只是处理特殊情形下的稳健估计问题,且缺乏对估计参数性质的研究。Ghosh等提出了针对区域水平模型的稳健贝叶斯预测量,并用于克服由离群观测造成的过度收缩问题[11],但并没有考虑离群值对模型系数的影响。Sinha和Rao利用Huber-Ψ函数,通过对由离群值引起的项减小权重的方式,建立了单元水平模型的小域稳健估计量[12]。目前,该方法普遍应用于小域稳健估计。在稳健估计的其他研究方面,Smith等用稳健投影和分位数的方法研究了商业调查中的小域稳健估计[13],Bertarelli等通过偏差修正的方式研究了小域稳健估计问题[14],Jiang和Rao对稳健小域估计的研究历史进行系统总结后指出,在以后的研究中,小域估计方法可应用于大数据、关联数据等领域,同时其他的现代统计方法、学科理论也可以用于小域估计[15]。由此可见,小域估计的稳健估计研究仍需要进一步的完善,探索具有普适性的估计方法成为该类研究中不可或缺的内容。本文重点关注更普遍的假设条件下稳健小域估计,并给出估计方法和步骤。
在统计推断中,当观测数据存在严重的离群值时,基于密度的最小距离方法成为解决问题的一种有效方法。Basu等提出用最小化密度幂散度(MDPD)的方法来得到参数的稳健估计,其核心思想就是给离群观测项赋予更小的权重,从而获得更加稳健的估计量[16]。在密度幂散度(DPD)类方法中,通过一个调整参数α(0<α<1)来调整参数的稳健性和估计有效性之间的平衡,随着α增大,模型估计的效率降低而稳健性增加。一般该类方法需要通过选取调整参数,损失一点有效性而达到稳健性的目的。Jones等提出了基于γ散度的稳健估计方法[17]。该方法与DPD方法同属基于密度的最小距离方法,应用于稳健估计和回归等方面[18]。考虑到该类方法在稳健估计中的优异性质,本文将γ散度引入小域估计中用于解决小域估计中的稳健性难题。
在本文中,将γ散度应用于单元水平的小域估计模型,考虑模型误差有偏和存在离群值情形下,讨论模型的随机误差和区域误差被污染时的稳健估计问题。首先,提出基于γ散度的单元水平模型的参数估计方法,给出参数估计方程和估计算法,讨论了参数的渐近性质。其次,给出了有限总体区域均值的估计量,并根据估计参数的渐近性质,给出了稳健调节参数γ的选取算法。进一步利用Bootstrap方法给出了稳健估计量MSE的估计。最后,通过模拟数据和实际数据对本文提出的估计方法进行了模拟验证,并与Sinha和Rao的稳健估计方法进行了对比[12],验证了本文稳健估计方法的有效性。
二、模型及参数估计
(一)模型

当抽样得到的数据和辅助信息都是单元级别的数据时,单元水平模型成为了小域估计的有力工具。误差嵌套模型(Nested Error Regression model,NER)是最基本的单元水平模型,由Battese等提出[2]。其具体模型如下:
(1)
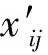
不失一般性,本文假设抽样得到的数据满足式(1)所示的模型,则由样本数据构成的模型可以写成如下的矩阵形式:
(2)
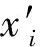
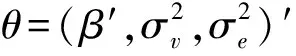
(3)
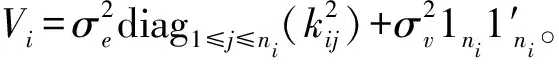
利用Sherman-Morrison公式可求出Vi的逆矩阵,
(4)
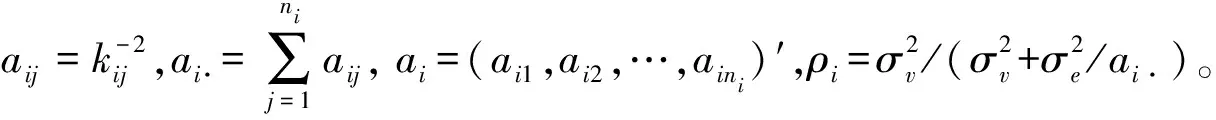
(二)γ散度及参数估计
假设某一总体未知的真实密度函数为g(x),用参数模型fθ(x)=f(x;θ)估计g(x),其中θ∈Θ,Θ为θ的所有可能的取值构成的p维参数空间。γ散度用于衡量两个概率密度之间的差异程度,γ散度的定义如下:
(5)
其中,γ>0是调整参数,θ为待估的未知参数。根据Kawashima和Fujisawa关于γ散度的论述[18],当γ→0时,式(5)中的γ散度退化为Kullback-Leibler(KL)散度,且最优的参数通过最小化式(5)得到。式(5)中的第一项与未知参数无关,因此最小化γ散度的问题变为:
(6)
式(6)中,当γ→0时,最小化γ散度的方法就退化为极大似然估计(MLE)。一般用抽样数据的条件经验分布函数来替代式(6)中的密度函数g(x),则上述目标函数可以写成:
(7)
称式(7)为γ似然函数。将式(3)的条件密度函数带入式(7),便可得:
(8)
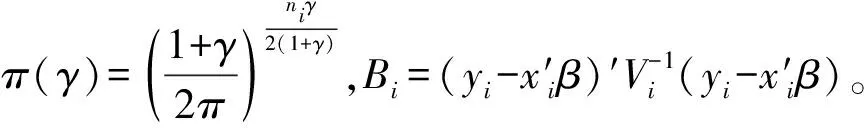
对式(8)的γ似然函数关于θ的每个分量求偏导数,便可得参数估计方程:
(三)估计参数的性质
为了便于标记,定义:
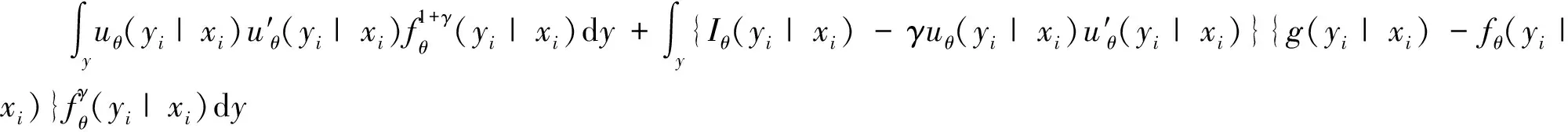
(1)存在参数空间Θ中的开集Λ包含最佳拟合参数θ,使得θ∈Λ时,J是正定矩阵。
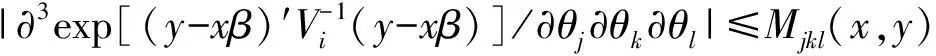
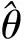
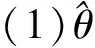
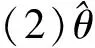
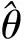
若θg是θ的真实值,对上式在θ=θg处进行泰勒展开,化简可得:
其中,Rm是泰勒展式中的余项。利用弱大数定律可知:
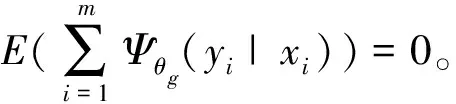
该定理说明了估计参数的一致性和渐近分布,在渐近分布的计算中,J(i)、K(i)中均含有未知的真实密度函数g(yi|xi),因此直接进行计算是难以做到的。在基本假设条件中,假定密度族fθ(yi|xi)中包含真实的密度函数,因此在J(i)、K(i)、ξ(i)的定义中,用fθ(yi|xi)替换g(yi|xi)进行估计。
从J(i)、K(i)、ξ(i)的定义中不难发现,当把矩阵J(i)认为是γ的函数时,矩阵K(i)可以表示为:K(i)=J(i)(2γ)-ξ(i)ξ(i)′,因此,矩阵K可以表示为:
通过上述协方差矩阵的计算可知,γ增大时参数方差增大,这说明MDPD估计量的效率随γ增大而减小。这一点进一步验证了优化参数γ用于控制MDPD估计量的效率和鲁棒性之间的权衡,当γ增加时稳健性增强效率降低。然而,后面的模拟实验表明这种效率的损失并不大。
(四)调整参数的选取
从上述结果中不难发现,利用DPD方法迭代得到的参数θ的估计表达式中,含有未知的调整参数γ。而γ的选取决定着稳健性和有效性的平衡,当γ的取值越接近于1,则估计得到的参数具有更强的稳健性,反之,稳健性越弱,有效性越强,因此选取适当的调整参数γ是稳健估计中很关键的因素。目前关于调整参数选取的方法主要有两种,一种是根据有效性和稳健性的占比关系,研究者根据自己的需求确定两者之间的占比,在此基础上,选取最优的调整参数。另一种方法是基于数据驱动的参数选择方法,Warwick和Jones通过最小化估计参数的MSE得到最优的调整参数[19]。但是,该方法依赖于初始值的选取,不同的参数初始值可能会产生不同的调整参数。Basak等在Warwick和Jones的研究基础上,提出了不依赖于初始值的调整参数选择方法[20]。本文采用Basak等提到的参数选取方法,选择最优的调整参数,用于构建稳健小区域估计量。
对于未知参数θ的真实值θ*最优的调整参数γ通过最小化MDPD估计量的MSE来获得,即:
(9)
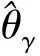
算法 IWJ算法
重复:1.利用WJ算法最小化正文中的式(9),并在γ的取值区间Iγ内更新γ:
2.固定γ(i+1),将其带入最小化γ散度的估计方程并更新得到θ*(i+1);
3.重复1、2,直至|γ(i+1)-γ(i)|<ε或|θ*(i+1)-θ*(i)|<ε*,其中ε、ε*为估计精度。
输出:γ(i+1)。
三、稳健小域估计量
(一)稳健经验贝叶斯预测量
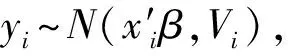
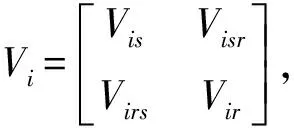
结合上述单元水平模型的假设,在抽样数据yis的条件下,yir的条件分布为:
yir|yis~N(μir|s,Vir|s)
(10)
其条件均值和条件协方差矩阵分别为:
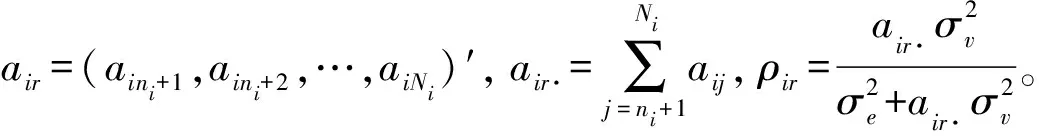
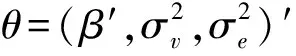
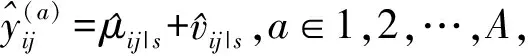
(11)
(二)区域均值的EBP
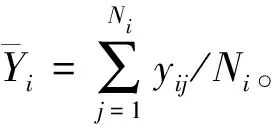
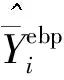
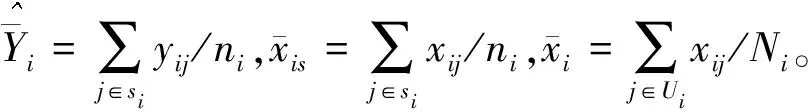
(三)区域EBP的MSE
估计单元水平模型的均方预测误差(MSPE)通常是比较困难的,原因有二:其一,单元水平模型中误差项和未抽中样本单元所服从的真实分布并不知道,从而无法获取密度函数进行MSPE的计算;其二,有时即便知道未抽样单元的分布,由于单元水平模型涉及的是单元层级的数据,在计算其期望的过程中会出现多重积分,这对MSPE的计算造成了极大的挑战。
在本文中,利用Sinha和Rao中提到的参数bootstrap方法来估计MSPE[12]。具体估计步骤如下:
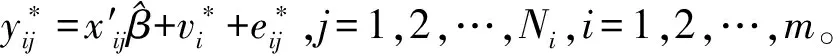

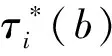
四、数值模拟与实例分析
(一)数值分析
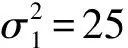
在模拟实验中,重点比较传统的极大似然方法(ML)、Sinha和Rao提到的稳健估计方法(RML)[12]以及本文提出的取不同调整参数(γ=0.1,0.2,0.3)时的稳健最小化γ散度的方法(RMG)。在RMG方法中,通过两种方式选取了调整参数γ,第一类为固定选取调整参数γ为0.1、0.2、0.3;第二类为使用IWJ算法选取的调整参数。将选取的调整参数带入参数估计方程,则可得模型参数的数值估计,其估计的平均结果见表1。首先比较四种污染情形下的模型参数的估计。表1给出了几种稳健估计方法在不同污染情形下的参数估计的偏差和均方误差,其中每种方法对应的第一列表示估计的偏差,第二列表示相应的MSE。
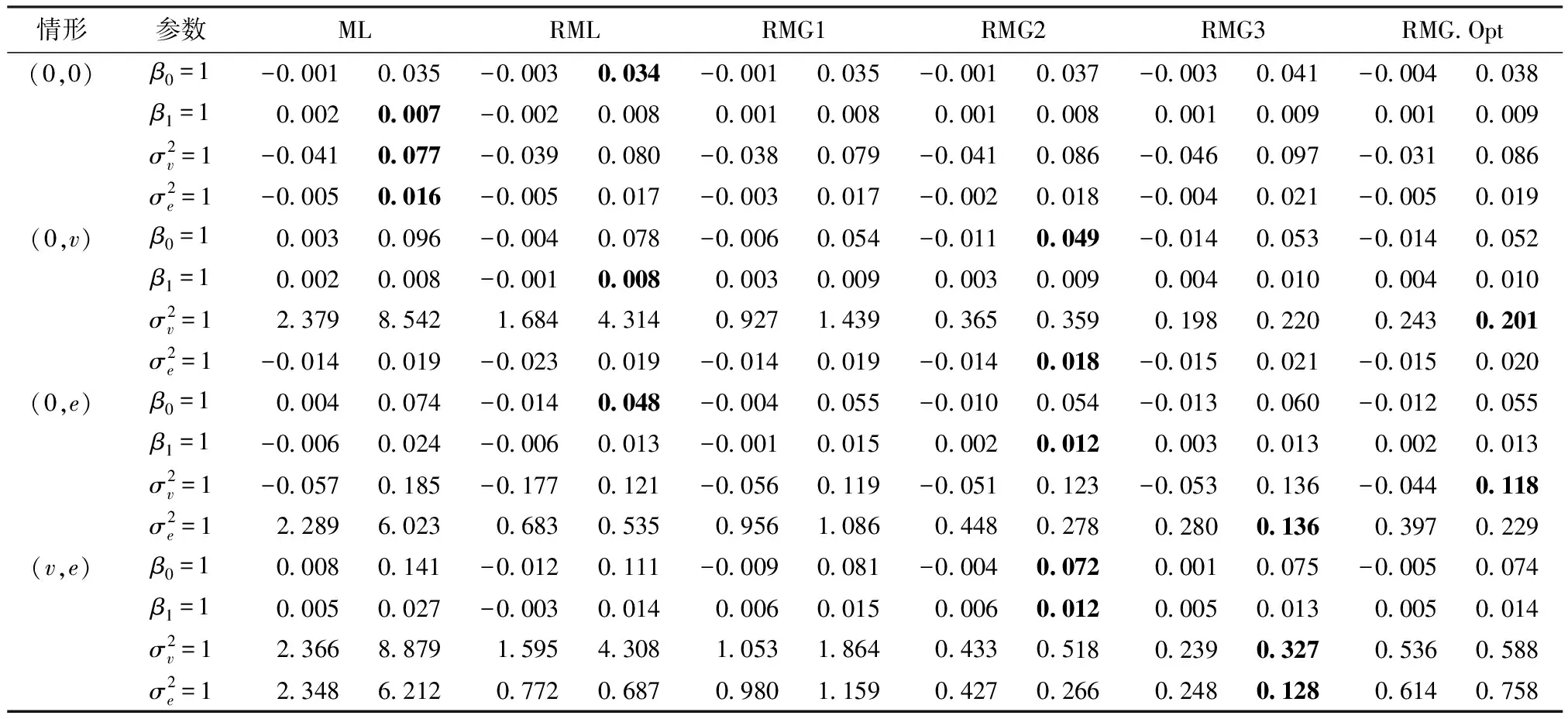
表1 四种污染情形下模型参数估计的偏差和MSE
从表1可以得出结论:当随机误差未被污染时,ML方法在参数估计中表现最好,但是RML以及具有较小调整参数的RMG方法和ML估计结果非常相近,说明在这种情形下,具有较小调整参数的RMG方法、RML与ML方法是几乎一样有效的,其偏差和MSE相差都不多。具有较大调整参数的RMG方法表现不好,恰好表明调整参数的选取至关重要,而最优调整参数可根据我们提供的算法得到。
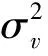
在区域效应和模型误差均被污染时,ML方法对方差部分的估计受离群值观测影响严重,以致于产生很大的偏差和MSE,RML方法减小了离群值带来的影响,但表现并非最好,RMG方法显著好于RML方法,只需要选取合适的调整参数即可。
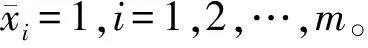

表2 四种污染情形下均值估计的偏差及其MSE
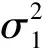
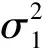
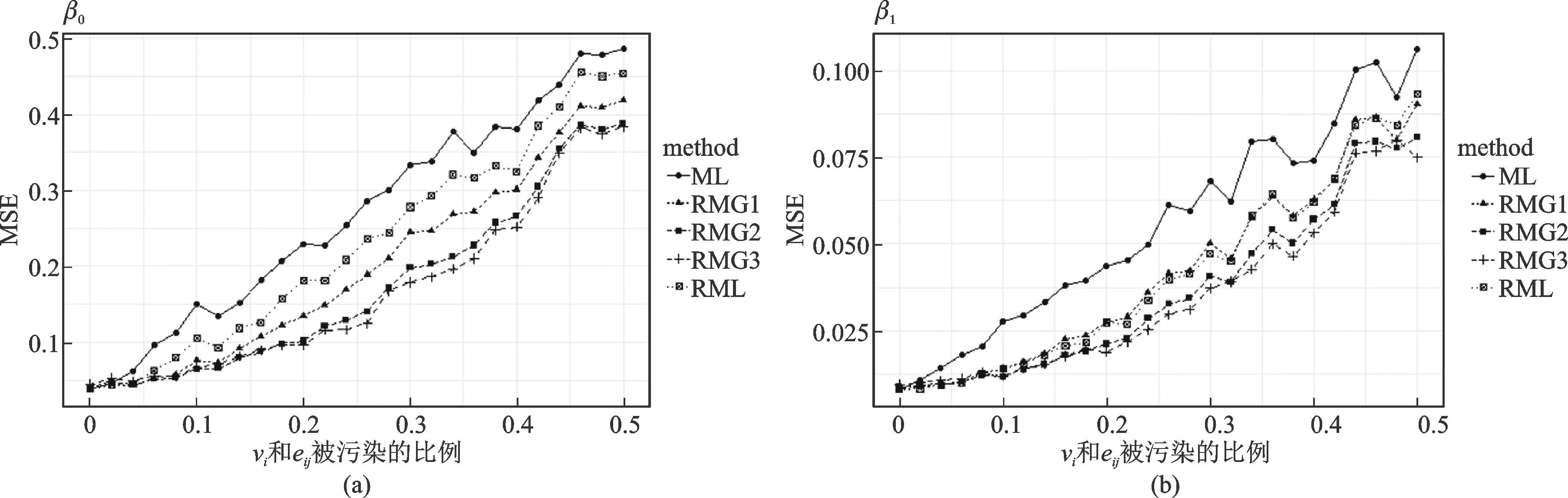
图1 模型系数的MSE随污染比例变化图
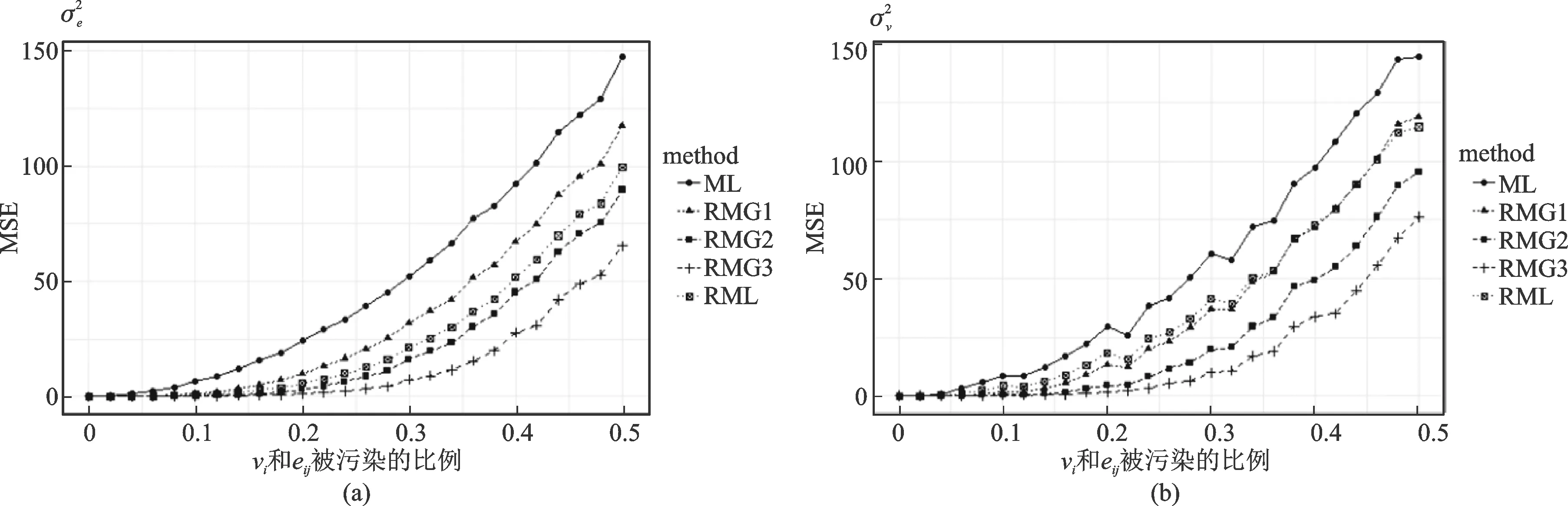
图2 估计方差的MSE随污染比例变化图
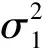
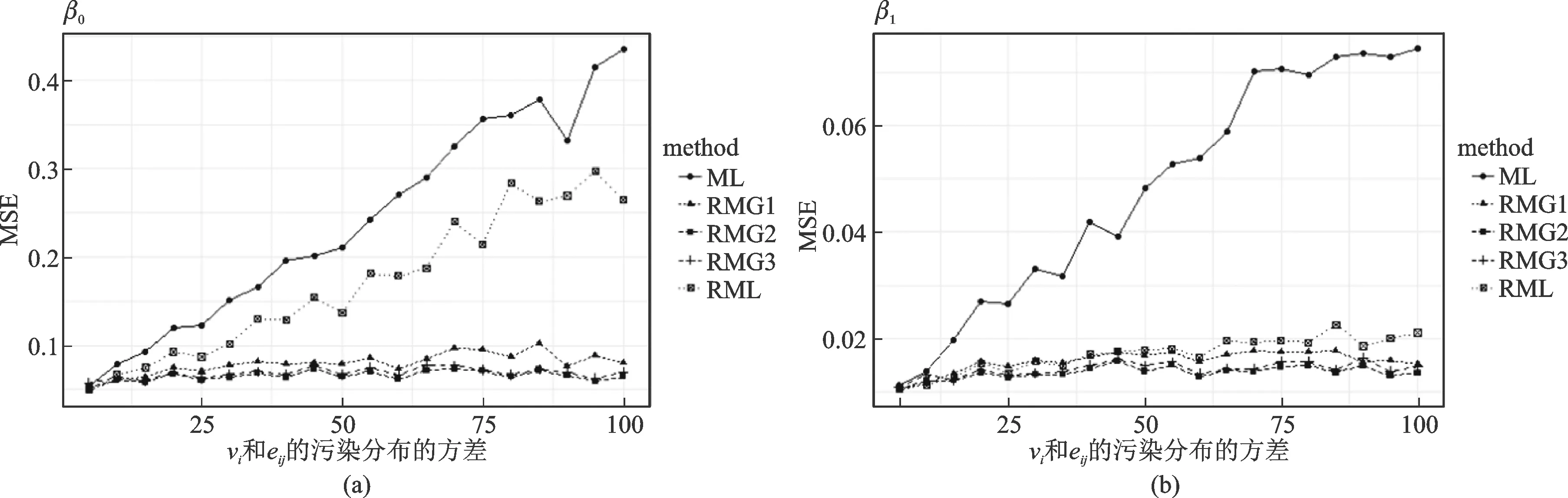
图3 模型系数的MSE随污染方差变化图
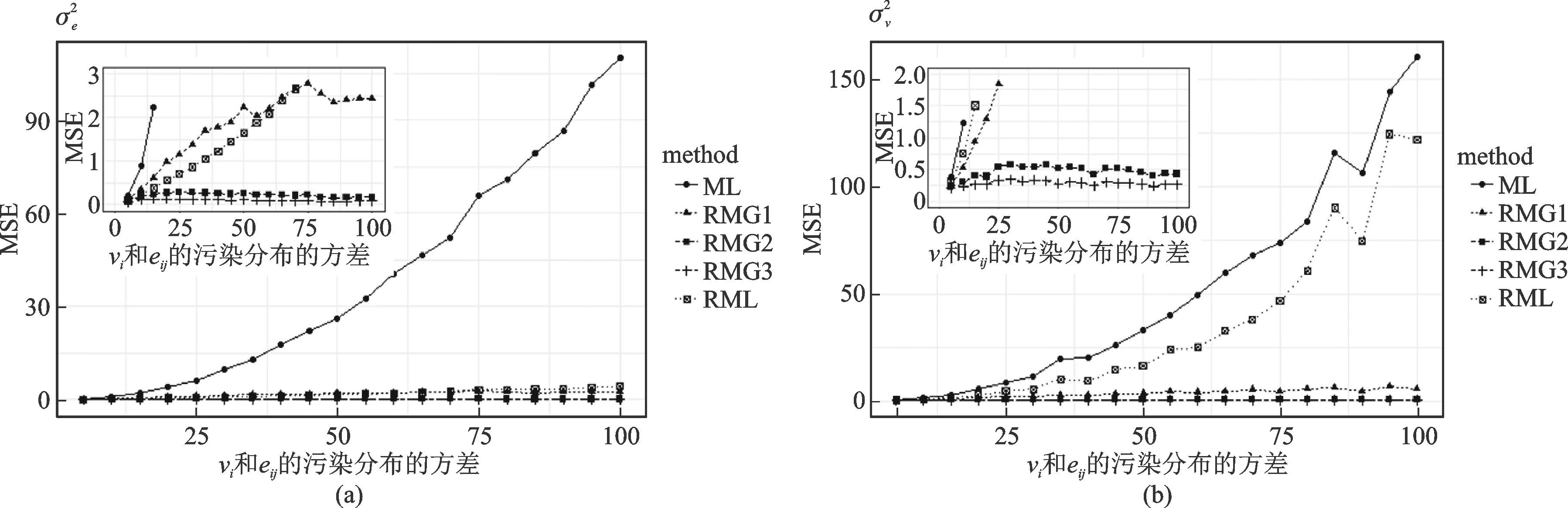
图4 估计方差的MSE随污染方差变化图
接下来考虑有限总体中小域均值的估计。比较在有限总体中用上述稳健估计方法得到的区域平均值的估计结果。设区域个数m=40,考虑区域总体数量Ni分别为40、80、200的情形下总体均值估计的表现。从第i个区域的Ni个单元中选取ni=4个单元作为随机观测样本。对每次模拟的数据集,可以利用上述模拟中提到的稳健方法获取每个区域上观测变量的均值,最后比较500次模拟之后区域均值的平均估计效果。
从表3的模拟结果上看,总的来说RMG方法在大部分情形下具有更小的MSE,在某些情形下虽不及RML方法的估计效果,但相差不大。另外,当区域尺度变大时如Ni=200,RMG方法得到的估计量具有更小的MSE,估计效果好于传统的估计方法。
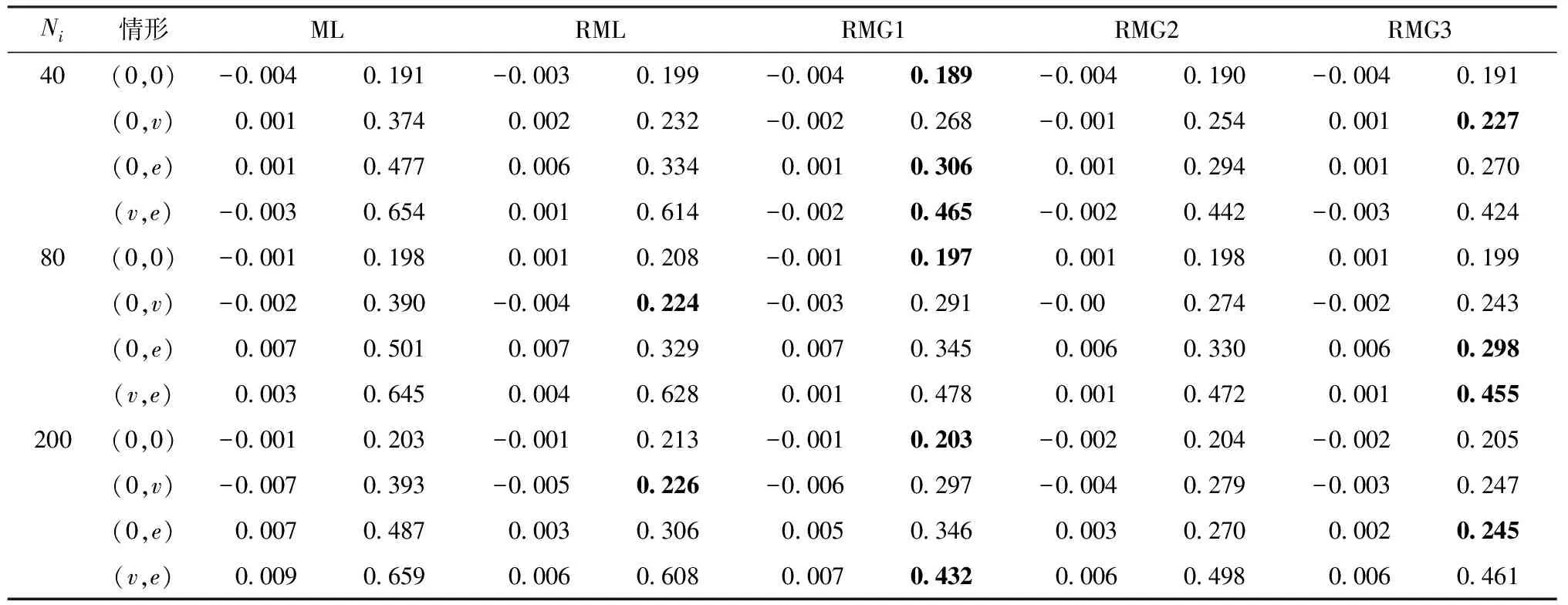
表3 不同污染情形下有限总体均值估计的偏差及其MSE
(二)实例分析
下面采用Battese等给出的数据(1)该数据由Battese等(1988)给出,主要结合了农作物种植面积的抽样数据和卫星观测数据,用于估计爱德华州12个县的玉米和大豆的种植面积。来验证本文提出的稳健估计方法[2]。该数据可以从R包sae中获得,其中包含了来自于12个县区的玉米和大豆的面积样本数据37个,以及每个区域上的玉米和大豆的像素值。用农场采访收集的数据作为因变量,卫星数据作为辅助变量,建立单元水平模型。
该模型可以作为模型(1)中kij=1,xij=(1,xij1,xij2)′的特殊情形。其中,yij表示第i个县第j个区域的玉米(大豆)的亩数,xij1和xij2分别表示第i个县第j个区域的玉米、大豆的像素值。
Battese等将Hardin县的值识别为离群值,并且在预测玉米和大豆的面积时只是将这一观测值简单地删除。Sinha和Rao则利用稳健估计方法对这一数据进行了分析,并给出了存在离群值时相应的预测值[12]。在这里,运用本文提出的方法对该数据进行建模分析,对每个区域上的玉米种植面积进行估计和预测。在用提出的方法进行预测估计之前,首先选取适当的参数γ,根据IWJ算法得出适用于该数据的最优γ=0.01。由于本数据中仅存在一个离群观测,因此在提出的稳健估计方法中,选取γ=0.01、0.05两种情形进行估计。在表4中给出了利用ML方法、RML方法以及本文的RMG方法估计得到回归系数和随机误差的方差。同时表中括号内给出了根据渐近分布得到的每个参数的标准误。结合表中数据比较而言,在调整参数γ=0.01时,用RMG方法估计得到的系数介于ML方法和RML方法得到的估计值之间。当调整参数γ增加到0.05时,模型估计的系数有了显著的变化。通过比较表4中展示的参数的标准误,可见用本文的方法估计得到的参数具有更小的标准误。
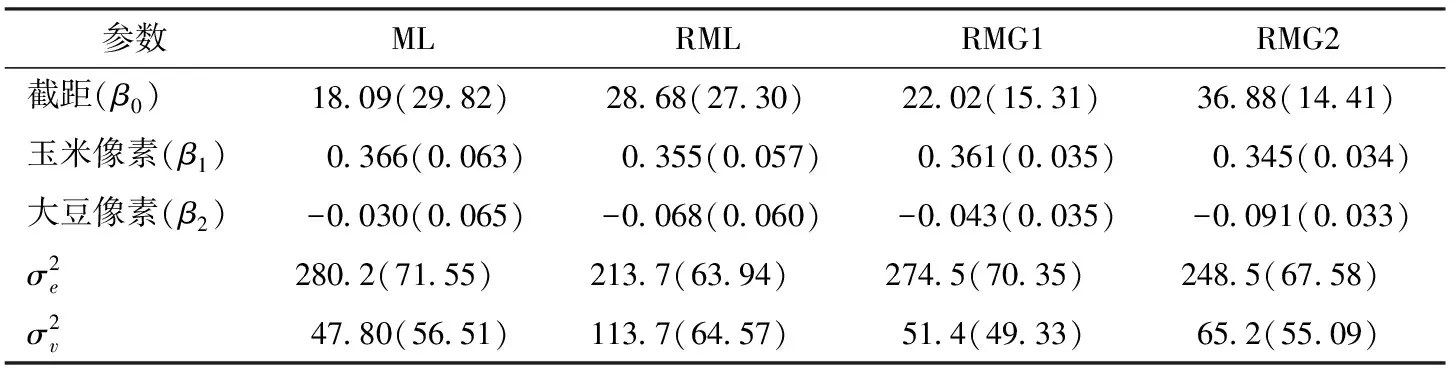
表4 模型参数的估计及其标准误
为了体现估计的效果,比较了几种估计方法对每个区域上玉米种植面积平均亩数的预测。由于每个区域上玉米种植面积的真实值并不知道,因此重点分析估计值的MSPE。采用上述估计方法得到的EBLUP值在表5中,其中括号内展示了用500个bootstrap样本得到的估计量的MSPE的估计值。
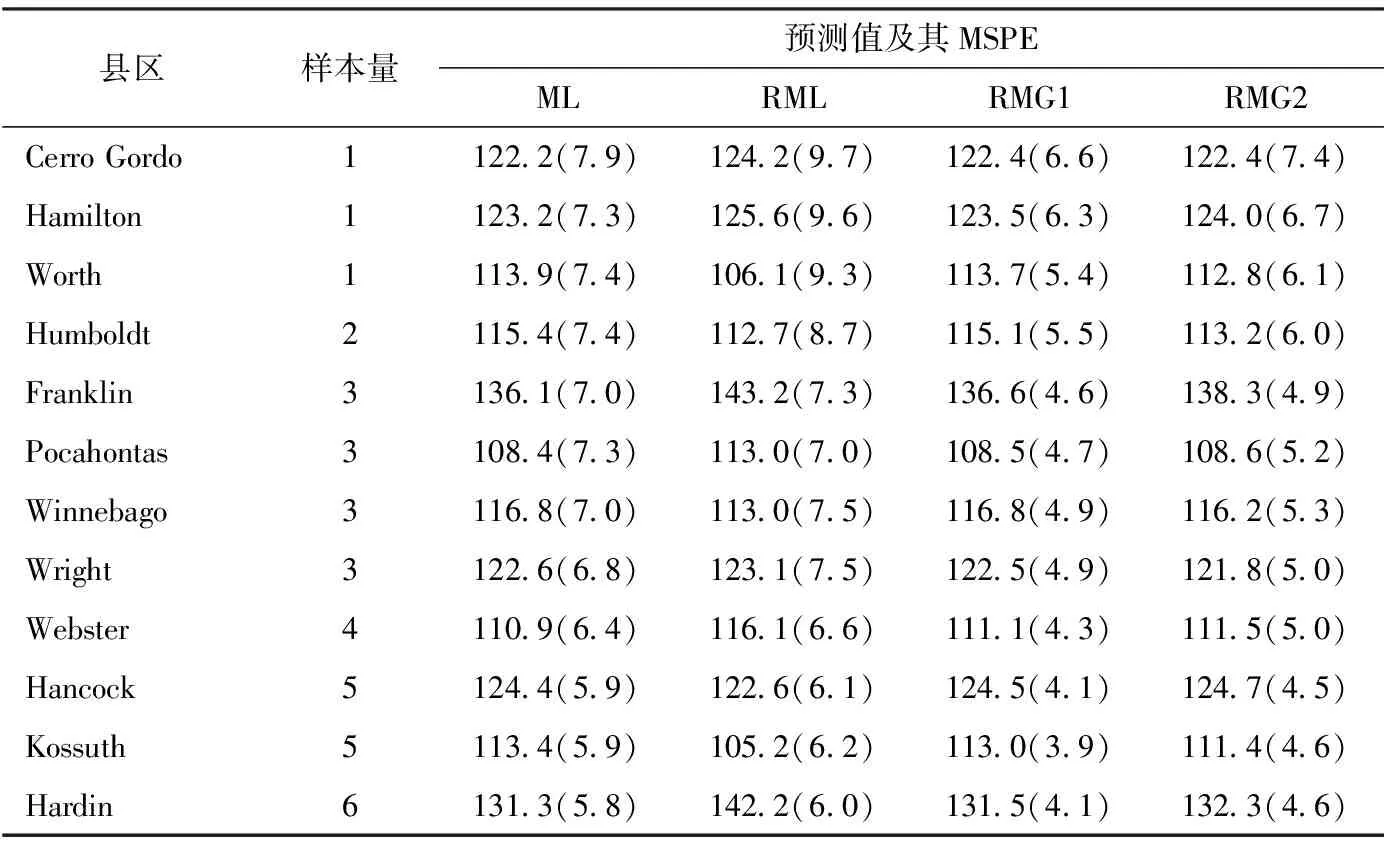
表5 区域玉米种植面积的预测及其Bootstrap MSPE
首先从估计结果上来看,RMG对没有离群值区域的估计更接近ML的结果,并且对区域Hardin的预测有了一定的改进。其次,通过比较bootstrap MSPE,提出方法RMG1和RMG2比其他两种估计方法得到的MSPE值更小,且最优调整参数γ=0.01时的RMG1表现更好。可见,RMG方法是有效的。
五、结论与研究展望
本文提出了一种针对存在离群观测值的单元水平模型小域稳健估计方法。通过引入MDPD方法,给出了解决具有离群观测和非正态分布误差的稳健估计方法。首先,给出了单元水平模型参数的估计方程和渐近性质。其次,结合参数的渐近分布,给出了最优调整参数的选择程序。再次,给出了有限总体中单元和区域均值的EBLUP值和估计量的MSE。最后,通过模拟数据和实际数据验证了本文提出方法的优越表现。在模拟部分,模拟了分布被污染时的稳健估计,讨论了三种污染情形下几类稳健估计方法的效果,还特别讨论了污染比例变化以及污染分布的方差变化时几类估计方法的MSE的变化情况。同时模拟结果表明,本文提出的方法能更好地解决这种离群情况。实际数据中,用一个小区域估计中很经典的数据说明本文提出的方法不仅十分有效,还能够很好地处理离群观测这一特殊情况。
进一步的验证表明,本文的方法针对随机效应服从其他有偏分布时也是有效的。当随机误差的分布被污染,且污染概率大于0.3时,本文的方法表现一般,比Sinha和Rao研究中的稳健估计方法差[12],但是在这种情形下,几类方法得到的MSE均很大,稳健估计结果都不太有价值。下一步,应尝试将本文方法进一步推广应用于指数分布情形的小区域估计问题。在本文的模拟实验部分,仅展示了模型误差项分布来自于混合正态分布时的估计结果。实际上,当模型误差项分布属于其他情形的有偏估计时,本文提出的估计方法都是适用的。例如当模型误差来自于t分布、对数正态分布、伽马分布等情形时,本文提出的稳健估计方法具有更小的偏差和均方误差,是一致有效的。这一点进一步说明该方法的普适性,能够在更一般的模型假设条件或存在离群观测时使用,并得到较为理想的估计结果。
在本文的研究基础上,还可以做如下工作:有关小域稳健估计的应用方面,Tang等提出了一种全局—局部收缩限样的方法来刻画小域估计中的随机效应,在贝叶斯分析的框架下给出了参数和目标变量的后验估计[21]。与本文提出的稳健估计不同,该方法主要适用于区域数量较大的区域水平模型。Kurisu等利用了和本文同样的估计方法,给出了区域水平模型的置信区间的估计[22]。类似地,可以在本文的基础上给出单元水平模型的置信区间估计。在本文的稳健估计方法中,调整参数的选取采用了IWJ算法,而Sugasawa和Yonekura给出了最小化密度幂类方法的调整参数选择的另外一种方法[23]。因此,在本文的研究框架下,同样可以采用Sugasawa和Yonekura提出的方法来选择调整参数,从而达到稳健小域估计的目的。

