翻折多变化,动态显身手
——立体几何中的翻折问题
■江苏省高邮市第一中学 徐晓霞
立体几何中的翻折问题是高考试卷中的一类创新题型,借助平面图形的翻折变成空间图形,进而借助平面图形的数量、位置等“变”与“不变”之间的联系,合理构建空间图形中的相关元素间的数量、位置关系,进而来解决一些相关的立体几何问题。此类问题能很好地考查同学们各方面的能力与素养。
一、线段长度问题
例1如图1,在平面四边形PDCB中,PD∥BC,BA⊥PD,PA=AB=BC=2,AD=1。如 图2,将△PAB沿BA翻折到△SAB的位置,使得平面SAB⊥平面ABCD。
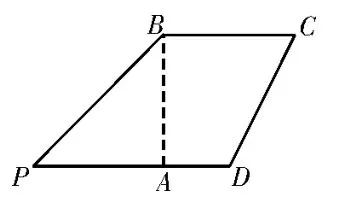
图1
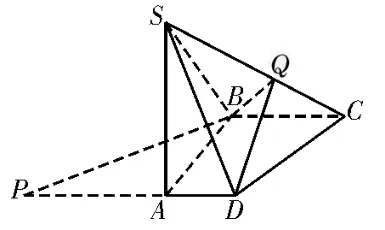
图2
(1)设平面SDC与平面SAB的交线为l,求证:BC⊥l;
(2)点Q在线段SC上(点Q不与端点重合),平面QBD与平面BCD夹角的余弦值为,求线段BQ的长。
解析:(1)依题意,AD⊥AB,因为PD∥BC,所以BC⊥AB。由于平面SAB⊥平面ABCD,且交线为AB,又BC⊂平面ABCD,所以BC⊥平面SAB。
因为l是平面SDC与平面SAB的交线,所以l⊂平面SAB,故BC⊥l。
(2)由(1)可知,AD⊥平面SAB,所以AD⊥SA,由题意可知SA⊥AB,AD⊥AB。
以A为坐标原点,AD,AB,AS所在直线分别为x轴,y轴,z轴,建立如图3 所示的空间直角坐标系A-xyz,则A(0,0,0),B(0,2,0),C(2,2,0),D(1,0,0),S(0,0,2),可得=(1,-2,0),=(2,2,-2)。
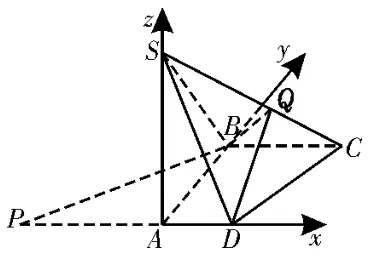
图3
二、空间角问题
1.线面角
例2如图4,在四边形ABCD中,AB=AD=,BC=CD=4,且AB⊥AD。如图5,将△BCD沿着BD翻折,当三棱锥C-ABD的体积最大时。
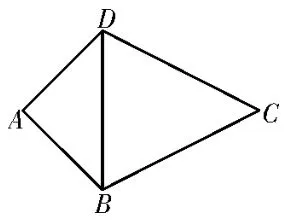
图4
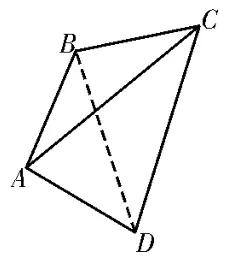
图5
(1)求此时三棱锥C-ABD的体积;
(2)求此时直线AD与平面ABC的夹角的正弦值。
解析:(1)在△BCD沿BD翻折的过程中,当平面ABD⊥平面BCD时,三棱锥C-ABD的体积最大。由平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,取BD的中点O,连接AO,则AO⊥BD,所以AO⊥平面BCD。又AB=AD=2,BC=CD=4,AB⊥AD,故BD=4,所以△BCD为正三角形。在△BCD中,BD边上的高为2,则(V三棱锥C-ABD)max=
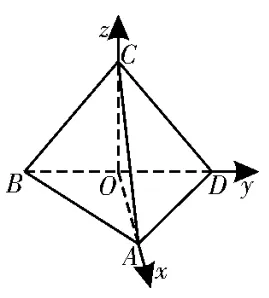
图6
2.二面角
例3如图7,四边形ABCD是等腰梯形,DC∥AB,DC=2,AB=4,∠ABC=60°,过D点作DE⊥AB,垂足为E。如图8,将△AED沿DE折到△A′ED的位置,且A′C=2。
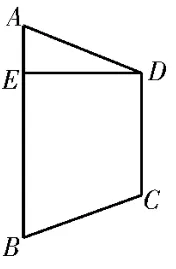
图7
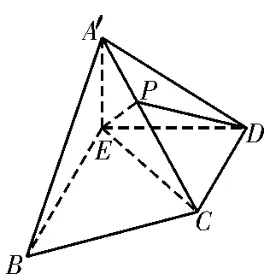
图8
(1)证明:平面A′ED⊥平面EBCD;
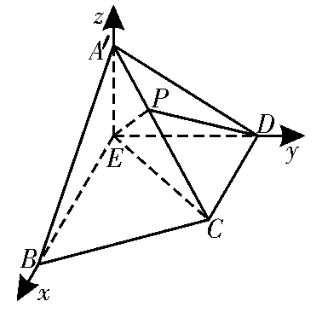
图9
三、空间距离问题
例4如图10,在等腰梯形ABCD中,AB∥CD,AB=2CD=2AD=2,∠ABC=60°。如图11,将△ACD沿着AC翻折,使得点D翻折到点P的位置,且AP⊥BC。
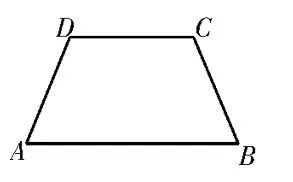
图10
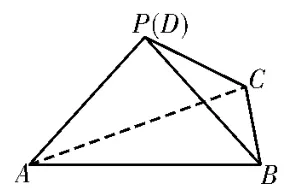
图11
(1)求证:平面APC⊥平面ABC;
(2)求点C到平面APB的距离。
解析:(1)在△ABC中,AB=2,BC=1,∠ABC=60°,由余弦定理得AC2=AB2+BC2-2AB·BC·cos 60°=3,所以AC2+BC2=AB2,所以BC⊥AC。而BC⊥AP,AP∩AC=A,所以BC⊥平面APC。又BC⊂平面ABC,所以平面APC⊥平面ABC。
立体几何中的翻折问题,看似背景简单,其实内涵深远,在很大程度上优化并改善同学们对立体几何的思维定式,合理构建空间立体几何直观图,使得静态数学动态化,让平面图形“立”起来,提升空间想象能力,优化数学思维品质。

