立体几何中外接球与内切球模型归纳
■安徽省芜湖市第一中学 周晓刚 江步云
近年来的高考和各级各类模拟考试中,立体几何的外接球和内切球问题,已成为常考常新试题,通常以选填题的形式出现,主要考查空间中的垂直与平行关系、空间距离、球的表面积和体积等知识。通过梳理高考真题和模拟题,不难发现该类问题可以归结为几类模型问题求解,在高考备考中,只要根据题目条件识别出问题所属模型,就可根据模型快速解题。下面笔者通过一些典型例题对立体几何中有关球的模型进行归纳,与读者交流,以期对同学们的高考备考能提供一些帮助。
一、外接球模型
模型一:正棱锥模型
由于正棱锥顶点的投影是底面的外心,由定心法可知正棱锥的外接球球心在底面的高上。若设正棱锥的高为h,底面外接圆的半径为r,外接球的半径为R,由图1,图2,图3知,对任意正棱锥,有OA=R,O1A=r,OO1=h-R(如图1,图3),或OO1=R-h(如图2)。根据勾股定理,可得到正棱锥外接球半径的通用公式为R2=r2+(h-R)2。
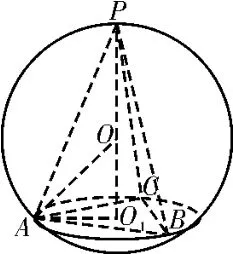
图1
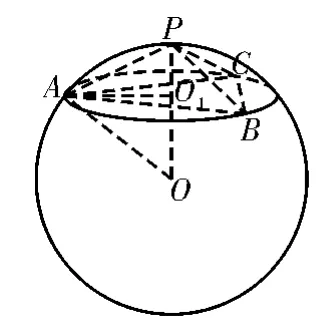
图2
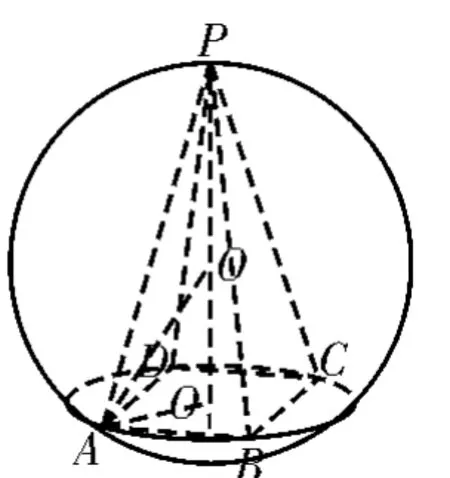
图3
例1所有棱长均为2的正四棱锥的外接球半径为____。
解析:易知底面(边长为2 的正方形)外接圆的半径r=,正四棱锥的高h=,根据公式R2=r2+(h-R)2,可得R=2。
模型二:线面垂直模型
众所周知,存在外接球的棱柱均为直棱柱,但直棱柱存在外接球的条件是底面存在外接圆。如图4,若设直棱柱的高为h,即OO1=,设底面外接圆的半径为r,即O1A=r,设外接球的半径为R,即OA=R。由勾股定理知R2=r2+,显然该公式对直棱柱的外接球具有一般适用性。而具有线面垂直特征的棱锥都可以补成一个直棱柱,而且该直棱柱和原棱锥具有相同的外接球。所以公式适用于所有具有线面垂直特征的棱柱与棱锥,其中R是外接球的半径,h是垂线段的长度,r是垂面外接圆的半径。
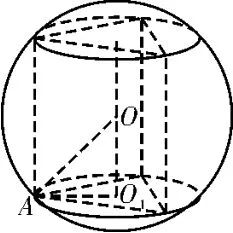
图4
模型三:增补成长方体的模型
众所周知,长方体的体对角线即为其外接球的直径。将棱锥增补成长方体的操作不仅仅局限于解决外接球问题,在截面等其他问题中也有类似操作。在这里我们主要阐述两种具体模型:对棱相等的三棱锥(如图5)、有三个面是直角三角形的三棱锥(如图6,图7,图8)。
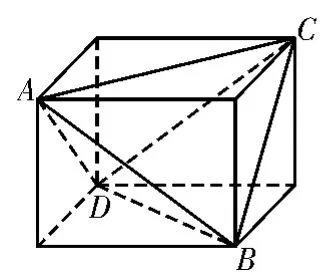
图5
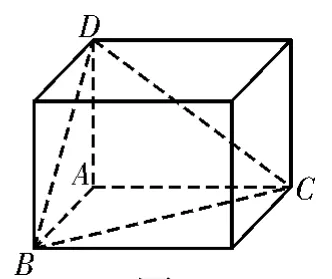
图6
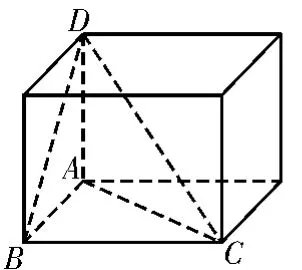
图7
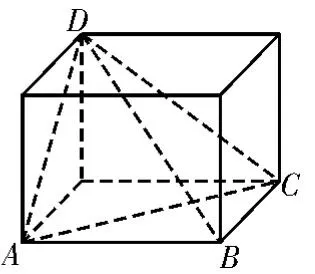
图8
例3在三棱锥D-ABC中,∠DAC=∠BCA=∠DBC=90°,BD=BC=5,且直线AC与BD所成角的余弦值为,则该三棱锥的外接球的表面积为____。
解析:观察到该三棱锥有三个直角但两两不共顶点,并没有线面垂直的特征,不符合模型二,所以只能增补成长方体(如图9)再作研究。直线AC与BD所成角即∠DBE,由cos∠DBE=知BE=3,DE=4,则外接球的直径为,表面积为4πR2=50π。
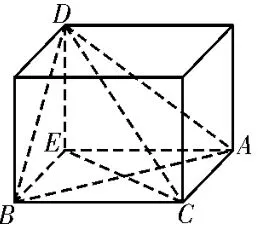
图9
模型四:一般模型
一般来说,除了上述三种特殊模型,其他均用一般方法——定心法解决。如图10,面ABC和面DEFG均是任意多面体的两个面,而O1,O2是这两个面的外心。由球的性质知过外心O1,O2分别作这两个面的垂线,两条垂线均过球心,即两条垂线的交点为球心,此为定心法。
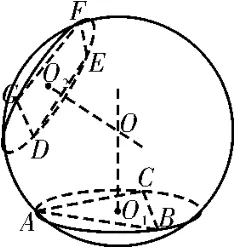
图10
例4如图11,在长方体ABCD-A1B1C1D1中,AB=2,BC=CC1=1,E,F分别为AB,CD的中点,则三棱锥D1-BEF外接球的表面积为_____。
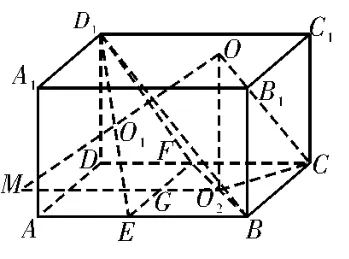
图11
评注:本题是定心法最一般的情况,也是最繁杂的情况,这种情况下会构造出四边形,而这个四边形的已知角是两个直角和一个二面角的平面角,已知边是二面角的平面角的两边,需要解出两条垂线段中的一条再进一步求半径。
例5已知四棱锥P-ABCD的底面ABCD是正方形,侧面PCD⊥平面ABCD,∠CPD=60°,AB=PD=2,则四棱锥PABCD的外接球的体积为____。
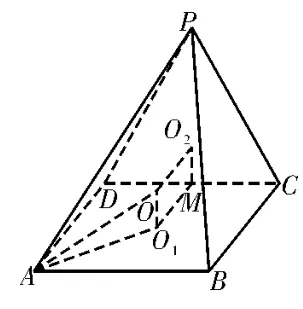
图12
评注:本题是将一般题型中的二面角特殊化为直二面角,难度大幅度下降。
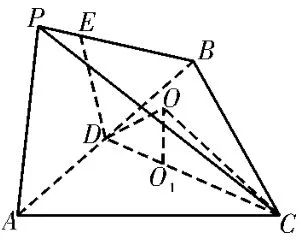
图13
评注:本题其中一个面的外心刚好在二个面的交线上,如同例4 中的四边形退化成直角三角形。
二、切球模型
模型一:多面体的内切球
如图14,球O为四面体A-BCD的内切球,由球的性质知四面体O-ABC,O-ABD,O-ACD,O-BCD的高均为内切球的半径r,则VA-BCD=VO-ABC+VO-ABD+VO-ACD+VO-BCD不妨设四面体A-BCD的体积为V,表面积为S,则r=。很显然此结论具有一般性,对所有具有内切球的多面体均适用。但应用此结论有两个前提:第一是必须为多面体,第二是必须为内切球。而第二点同学们容易将“几何体能打磨成(装下)最大的球”误以为一定是内切球,这一论断的前提是该几何体必须具有内切球。
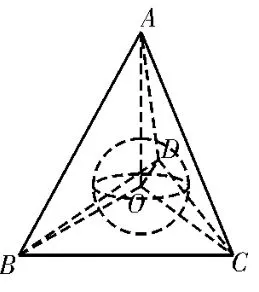
图14
例7(1)边长为2的正四面体的内切球的半径为____。
模型二:其他切球
内切问题内容丰富,除多面体的内切球外,还有旋转体的内切球、棱切球,以及多个球与几何体内切等。解决这类问题的思路基本一致,即探寻球心和切点。
例8三个半径为3的球两两相切放置在水平桌面上,则三个球与桌面围成的空间中能放置的最大球的半径为____。
解析:显然所求球与三个球和桌面均相切。设三个球的球心分别为O1,O2,O3,与桌面的三个切点分别为A,B,C,则三棱柱是一个底面边长为6,高为3 的正棱柱。如图15,设所求球的球心为O,半径为r,与桌面的切点为D,则三棱锥OO1O2O3为正三棱锥,底面边长为6,侧棱长为r+3。根据题意可求三棱锥O-O1O2O3的高为,而根据相切知OD=r,三棱锥O-O1O2O3的高又为3-r,则=3-r,解得r=1。
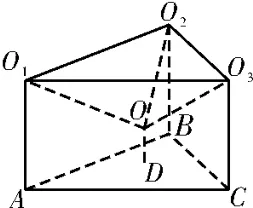
图15
评注:解决本题的关键在于确定四个球心和四个切点的位置。
关于外接球和内切球问题,解题的关键在于记住几个特征明显的模型,方便快速甄别,其他的模型均用一般方法解决。

