立体几何中动点轨迹问题的通性通法总结

■安徽省芜湖市第一中学 刘海涛

在立体几何的高考复习备考过程中,频繁出现有关动点轨迹的问题,该类问题一般以选择、填空题的形式出现,主要考查空间中点、线、面的平行与垂直关系,空间中的距离、角度,解析几何中的点的轨迹等知识,综合性强,难度较大,已成为高考复习备考的一大课题。本文通过几道典型例题归纳总结出有关立体几何中动点轨迹问题的通性通法,现与读者交流。

一、由动点保持平行性求轨迹

例1在棱长为2 的正方体ABCDA1B1C1D1中,E,F分别是棱C1D1,B1C1的中点,P是上底面A1B1C1D1内一点(含边界),若AP∥平面BDEF,则点P的轨迹长为( )。

解析:如图1 所示,分别取棱A1B1,A1D1的中点M,N,连接MN,B1D1。因为M,N,E,F为所在棱的中点,所以MN∥B1D1,EF∥B1D1,则MN∥EF。又MN⊄平面BDEF,EF⊂平面BDEF,所以MN∥平面BDEF。连接NF,由NF∥A1B1,NF=A1B1,A1B1∥AB,A1B1=AB,可得NF∥AB,NF=AB,则四边形ANFB为平行四边形,则AN∥FB。而AN⊄平面BDEF,FB⊂平面BDEF,则AN∥平面BDEF。又AN∩NM=N,所以平面AMN∥平面BDEF。又P是上底面A1B1C1D1内一点,且AP∥平面BDEF,所以点P在线段MN上。又MN=B1D1,所以点P的轨迹长为。故选B。

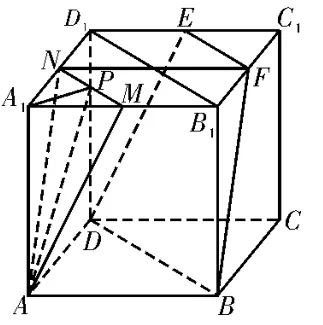
图1

评注:由P是动点,得AP为动直线,考虑将AP放入过定点A且平行于平面BDEF的平面(记为α)内,又P是上底面A1B1C1D1内一点(含边界),故P点的轨迹为所求平面α与上底面A1B1C1D1的交线(线段MN),于是只需确定M,N两点的位置即可。

通性通法:处理由一动点P(在某一定平面γ内或某空间几何体的表面Γ上)与一定点A形成的动直线AP与定平面β平行,求动点P的轨迹问题时,一般有两种处理策略:①将线面平行转化为面面平行,即过点A作平面α,使得α∥β,α与γ(或Γ)的交线即为动点P的轨迹;②利用法向量垂直关系求轨迹,即设点P的坐标得到直线AP的方向向量,利用·n=0(n为平面β的法向量),得到动点P的轨迹方程。

二、由动点保持垂直性求轨迹

例2在棱长为1 的正方体ABCDA1B1C1D1中,M,N分别为BD1,B1C1的中点,点P在正方体的表面上运动,且满足MP⊥CN。给出下列说法:①P可以是棱BB1的中点;②线段MP的最大值为;③点P的轨迹是正方形;④点P轨迹的长度为2+。其中所有正确说法的序号是____。

解析:如图2 所示,分别在棱CC1,DD1,AA1,BB1上取点E,F,G,H,使得C1E=D1F=AG=BH,连接EF,FG,GH,HE,FH,D1H,FB。在正方形CC1D1D中,由C1E=D1F,得EF∥CD,EF=CD。同理AB∥GH,AB=GH。又AB∥CD,AB=CD,所以EF∥GH,EF=GH,则四边形EFGH为平行四边形。由AB⊥平面BB1C1C,HE⊂平面BB1C1C,得AB⊥HE。又AB∥GH,所以HE⊥GH,故四边形EFGH为矩形,其中GH=1,HE=,FH=。在 正 方 形BB1C1C中,tan∠NCC1·tan∠HEC=×2=1,则∠NCC1+∠HEC=90°,所以CN⊥HE。由AB⊥平面BB1C1C,CN⊂平面BB1C1C,得CN⊥AB。又AB∥GH,所以CN⊥GH。又GH∩HE=H,所以CN⊥平面EFGH。由题知D1F∥HB,D1F=HB,则四边形D1FBH为平行四边形。又M为BD1的中点,则M也为FH的中点,所以M∈平面EFGH。由MP⊥CN,CN⊥平面EFGH,M∈平面EFGH,点P在正方体的表面上运动,得点P的轨迹为矩形EFGH,显然①和③错误,②和④正确。故填②④。

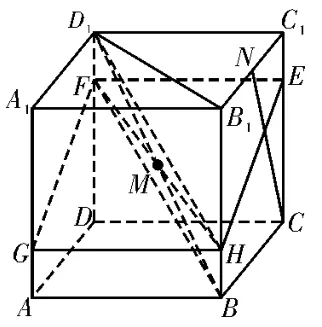
图2

评注:由P是动点,得MP为动直线,考虑将MP放入过定点M且与定直线CN垂直的平面(记为α)内,又点P在正方体的表面上运动,故P点的轨迹为所求平面α与正方体表面的交线(矩形EFGH),于是只需确定E,F,G,H四点的位置即可。

通性通法:处理由一动点P(在某一定平面γ内或某空间几何体的表面Γ上)与一定点M形成的动直线MP与定直线l垂直,求动点P的轨迹问题时,一般有两种处理策略:①将线线垂直转化为线面垂直,即过点M作平面α,使得l⊥α,α与γ(或Γ)的交线即为动点P的轨迹;②利用向量垂直关系求轨迹,即设点P的坐标得到直线MP的方向向量,利用·a=0(a为直线l的方向向量),得到动点P的轨迹方程。

三、由动点保持定距(或等距)求轨迹

例3在棱长为4 的正方体ABCDA′B′C′D′中,E,F分别是AD,A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′上运动,则线段MN的中点P的轨迹(曲面)与正方体(各个面)所围成的几何体的体积为( )。

解析:如图3 所示,连接PF,NF。在 正 方 形AA′D′D中,由E,F分别为AD,A′D′的中点,得EF∥AA′,且EF=AA′=4。由AA′⊥平面A′B′C′D′,得EF⊥平面A′B′C′D′。又FN⊂平面A′B′C′D′,所以EF⊥FN。又P为MN的中点,所以FP=MN=1,故点P的轨迹是以F为球心,1为半径的球面,则点P的轨迹(曲面)与正方体(各个面)所围成的几何体为球F的,所以所求几何体的体积为V=。故选D。

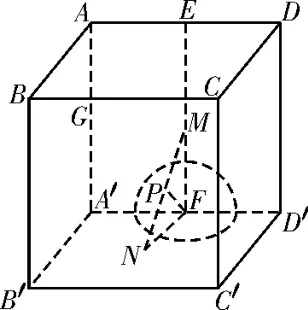
图3

评注:由M,N为动点知P为动点,得PF为动线段,连接PF,NF,发现PF为直角△MNF的斜边MN上的中线,又MN=2,则PF=1,由此得到动点P到定点F的距离为定值1,根据球的定义知点P的轨迹是以F为球心,1为半径的球面,问题转化为求球体与正方体的公共部分的体积。

通性通法:若由两个动点M,N(或一个动点M与一个定点N)构成的动线段MN的长度为定值,处理该线段的中点P的轨迹问题时,一般有两种处理策略:①根据问题特征,找到与M,N所在直线(或面)有关联的定点F,研究线段PF的长度是否为定值,根据题意判断点P的轨迹是球(或圆);②建立空间直角坐标系,将题中几何语言“翻译”为代数语言,得到动点P的轨迹方程。

四、由动点保持定角(或等角)求轨迹

例4在正方体ABCD-A1B1C1D1中,M,N分别为AB,A1B1的中点,P是边C1D1上的一个点(包括端点),Q是平面PMB1上一动点,满足直线MN与直线AN的夹角与直线MN与直线NQ的夹角相等,则点Q所在轨迹为( )。

A.椭圆 B.双曲线

C.抛物线 D.抛物线或双曲线

解析:由题设知,Q点的轨迹为以AN为母线,MN为轴,AB为底面直径的圆锥侧面,及其关于A1B1反向对称的锥体侧面与平面PMB1的交线,如图4所示。若P在边C1D1上移动的过程中,只与下方锥体有相交,则Q点轨迹为抛物线;若P在边C1D1上移动的过程中,与上方锥体也有相交,则Q点轨迹为双曲线。故选D。

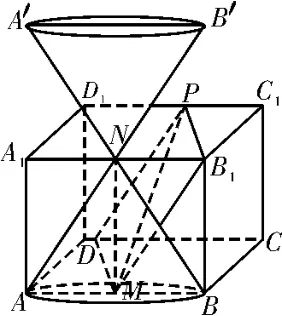
图4

评注:由题设知,直线MN与直线AN的夹角∠ANM为定值,则动直线NQ与定直线MN的夹角为定值,由此得动点Q的轨迹是以AN为母线,MN为轴,AB为底面直径的圆锥侧面,于是问题转化为动平面PMB1与圆锥体侧面的交线,应用数形结合,根据平面与双锥面相交所成曲线的性质判断点Q所在轨迹的形状。

通性通法:已知由一个动点Q(在某一定平面γ内或某空间几何体的表面Γ上)与一个定点N(在某一定平面α内)构成的动直线QN,两定点M,N构成定线段MN,若动直线NQ与定直线MN的夹角为定值(或动直线NQ与平面α所成角为定值),则动点Q的轨迹为圆锥体的侧面与平面γ(或表面Γ)的交线(一般为圆、椭圆、双曲线、抛物线的全部或一部分)。若需定量知道曲线的长度(围成的区域面积),则可借助空间直角坐标系,通过设动点Q的坐标,利用向量的夹角公式等,得到动点Q的轨迹方程。

例5如图5,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,AB∥CD,AB⊥AD,CD=AD==2,PA=3,若动点Q在△PAD内及边上运动,使得∠CQD=∠BQA,则三棱锥Q-ABC的体积最大值为____。

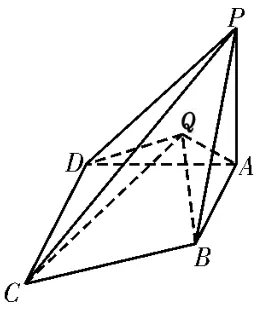
图5

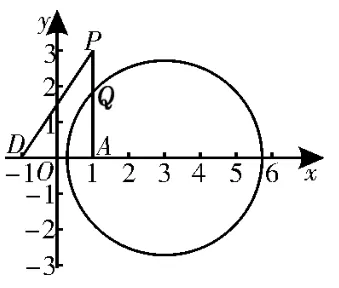
图6

评注:解答该题的关键是在得到QD=AD后,在平面PAD内,建立平面直角坐标系求出点Q的轨迹是圆(x-3)2+y2=8在△PAD的边上或内部的圆弧,由数形结合直观得出点Q到DA的距离最大为2,即三棱锥Q-ABC的高的最大值为2。

通性通法:已知由一个动点Q(在某一定平面γ内或某空间几何体的表面Γ上)与四个定点A,B,C,D,若∠CQD=∠BQA,则考虑解△CQD和△BQA,尝试将问题转化为动点Q到两定点D,A(或D,B,或C,A,或C,B)的距离相等(或成定比例),利用坐标系借助平面解析几何知识求出动点Q的轨迹方程。

五、投影求轨迹

例61822 年,比利时数学家旦德林(Dandelin)利用圆锥曲线的两个内切球,证明了用一个平面去截圆锥,可以得到椭圆(其中两球与截面的切点即为椭圆的焦点),实现了椭圆截线定义与轨迹定义的统一性。在生活中,有一个常见的现象:用手电筒斜照地面上的篮球,留下的影子会形成椭圆。这是由于光线形成的圆锥被地面所截产生了椭圆的截面。如图7所示,在地面的某个点A1的正上方有一个点光源,将小球放置在地面,使得AA1与小球相切。若A1A=5,小球的半径为2,则小球在地面的影子形成的椭圆的离心率为____。

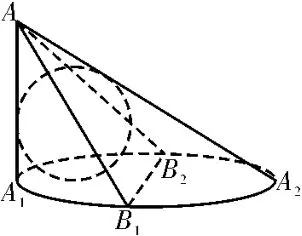
图7

解析:作出过A,A1,A2三点的截面,如图8 所示,设球与AA2相切于点D,球与A1A2相切于点F1(椭圆的左焦点)。在Rt△AA1A2中,设A2F1=x,则DA2=x,AA1=5,A1A2=x+2,AA2=x+3,所以52+(x+2)2=(x+3)2,解得x=10,则长轴长A1A2=2a=12,即a=6,c=6-2=4,所以离心率e=。故填

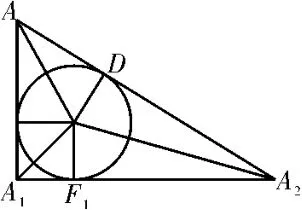
图8

评注:由题干中的介绍不难明白小球在地面的影子形成的椭圆,球与地面的切点为该椭圆的左焦点,于是考虑利用光线形成的圆锥的轴截面来解题,得到如图8 所示的平面图形,接着利用平面几何知识可轻松解题。

通性通法:一般地,球的正投影为圆,非正投影为椭圆,这是因为点光源的光线形成圆锥,被地面所截产生了椭圆的截面,其中球与地面的切点为椭圆的一个焦点。

六、翻折与动点求轨迹

例7已知矩形ABCD中,AB=1,AE=,如 图9 所示,将△ABE沿 着BE进行翻折,使得点A与点S重合,若点S在 平 面BCDE上的射影在四边形BCDE内部(包含边界),则动点S的轨迹长度为____。

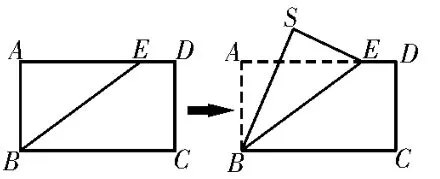
图9

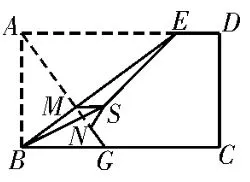
图10

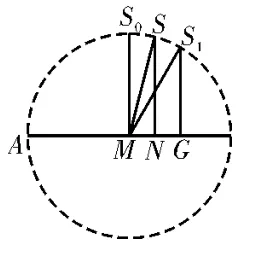
图11

评注:过点A作AM⊥BE于点M,交BC于点G,在翻折的过程中,不改变这一垂直关系,故可得到BE⊥平面SMG,从而平面SMG⊥平面BCDE,由面面垂直的性质定理不难得到,点S在平面BCDE上的射影N落在线段MG上。由翻折过程可知,SM=AM=判断出S的轨迹是以M为圆心,为半径的一段圆弧,求出圆心角,利用弧长公式求出弧长。

通性通法:立体几何中的翻折问题,看似变幻莫测,实则有据可循,一般情况下,需要始终牢记以下几点:(1)在折线同侧的量,折叠前后不变。(2)“跨过”折线的量,折叠前后可能会发生变化;这些变与不变的关系,构建了平面图形与空间图形之间的桥梁。因此,在解决立体几何翻折问题时,常见的解题策略有:①翻折过程中寻找不变的垂直关系求轨迹;②翻折过程中寻找不变的长度关系求轨迹;③可以利用空间坐标运算求轨迹。

立体几何中的动点轨迹问题,主要考查空间想象能力,分析变化中的不变量,考查的内容以教材中的公理和基本定理为主,若我们能熟练掌握这些基本公理、定理、概念、公式等,牢记文中归纳总结出的六大类型及其通性通法,定能轻松掌握立体几何中的动点轨迹问题。