基于不平衡电流拟合的差动保护可靠性评估

曾星星，高 原，杜继成，杨 洋，文 旭，白 江，蒋长江，樊 东，夏 春

（国家电网有限公司西南分部，成都 610041）

基于电流互感器（CT）的差动保护测量回路路径长且转换连接点多，容易出现接触不良、回路多点接地、电磁干扰、采取误差、极性接错及电磁饱和等问题[1-2]，从而降低了差动电流的测量准确性，以致影响差动保护可靠动作，严重威胁电力系统的安全稳定运行。

目前针对差动保护可靠性研究主要基于CT 误差机理的分析，进而对差动保护提出相应改进措施。罗苏南等[3]及王程远等[4]建立了CT 误差分析等值模型，指出励磁分流、铁芯剩磁及介质损耗是影响CT 误差的主要因素，并推导了CT 饱和误差计算公式。余保东等[5]进而基于CT 饱和误差特性对差动保护影响的分析提出了抗饱和电流差动保护措施。上述研究虽然减小了CT 饱和误差的影响程度，提高了差动保护的可靠性，但忽略了对其灵敏度的考虑。

对此，曹团结等[6]分析了CT 饱和误差关于一次电流变化特性，并提出了分段比率制动原理的电流差动保护，改善了差动保护的灵敏度。刘中平等[7]分析了重负荷下输电线路电流差动保护的灵敏度缺陷，提出一种改进的稳态电流差动判据提高保护灵敏性。袁宇波等[8]基于改进Hausdorff 距离算法提出一种新的差动保护原理，兼备速动性及抗CT 饱和特性影响。

差动保护能否可靠快速动作与所设定差动电流门槛值大小直接相关，而实际工程中不同类型和电压等级的差动电流特性存在差异，因此根据固定的差动电流门槛值去判断系统的故障情况是不全面的。然而，差动电流测量值的大小直接关系着保护装置能否正确动作，其数值不仅受到信号测量和处理精度的影响，还与系统一次电流和线路温度密切相关[6，9-11]，目前对此还鲜有文献研究。

为此，本文在深入剖析差动不平衡电流与其一二次电流及运行温度关系的基础上，利用BP 神经网络方法建立差动不平衡电流拟合关联函数，通过差动不平衡电流拟合值与整定值对比，提出电流差动保护可靠性评估新思路。

1 差动不平衡电流机理分析

1.1 差动不平衡电流产生原因

根据电流差动保护原理的基尔霍夫电流定律，差动电流为差动保护各连接支路二次电流的求和

式中：Icd为母线差动电流；I2i为连接于母线的各支路二次电流。

理想条件下，以电流互感器为核心的测量回路无误差，当系统在正常运行及区外故障时，差动电流为0，如式（2）所示。

实际工程中，由于各支路电流测量回路误差的影响，差动保护中将出现差动不平衡电流Iunb，如式（3）所示。

测量回路误差主要源自于CT 激磁阻抗所引起的激磁电流。图1 为电流互感T 型等值电路模型，Z2、Ze和ZL分别为CT 二次绕组阻抗、等效励磁阻抗和负载阻抗，I1、I2和Ie别为归算到二次侧的一次电流、二次电流和激磁电流。

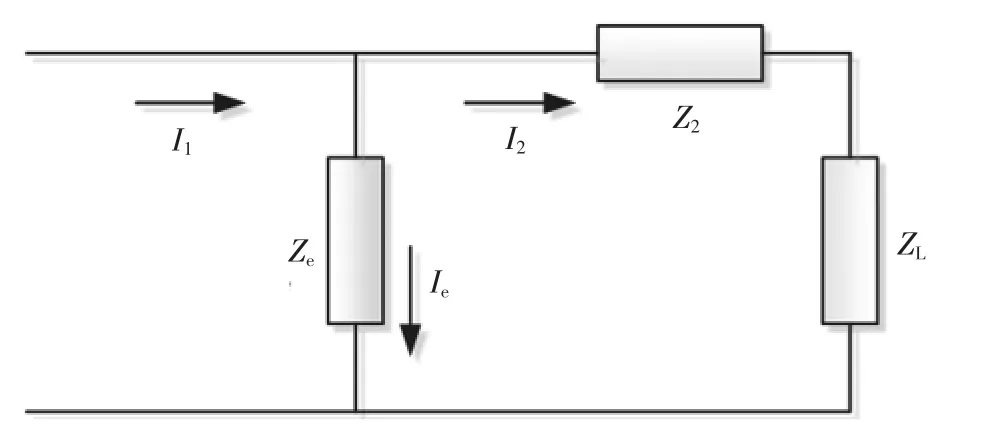
图1 电流互感器T 型等值电路

由于激磁电流Ie的存在，因此I1≠I2，即产生了电流互感器瞬时误差ε，其定义如下

式中：I1和I2分别为CT 瞬时变比一次电流和二次电流。

根据图1 所示的CT 等值T 型电路可得

由此，将式（5）代入式（4），ε 可进一步表示为

又将式（4）代入式（3），差动不平衡电流Iunb可进一步表示为

正常运行情况下，Z2+ZL≪Ze，CT 误差ε 近似为0。当差动保护各连接支路配置同型号CT 时，式（7）中各支路CT 误差相同，差动不平衡电流基本为0。

系统发生短路故障时，保护用CT 一次短路电流很大，一、二次电流及励磁电流中同时出现直流分量，使铁心磁场密度瞬间达到饱和值，从而使励磁阻抗Ze大大下降，由式（6）可知，电流互感器误差将显著增大。而且差动保护各连接支路CT 一次电流各不相同，即饱和程度存在较大差异，式（7）中各支路CT 误差各不相同，从而将产生较大的差动不平衡电流。

1.2 差动不平衡电流特性分析

电力系统故障情况下，CT 一次电流为大幅值正弦波，二次电流因CT 饱和特性发生畸变，且因磁场强度周期性变化而使铁心形成的交流磁滞回环进一步加深了CT 二次电流的畸变，从而使CT 二次电流含有不可忽视的高次谐波。由于差动保护性能与二次电流高次谐波紧密相关，国际电工委员会提出以复合误差作为保护用CT 在一次系统发生短路故障时的误差指标[5]。

式中：i1、i2分别为CT 的一、二次瞬时电流值；Ii为CT一次电流的有效值；Kn为CT 的额定变比，T 为一个周波的时间。

同时，根据索南加乐等[9]的研究可得CT 复合误差与一次电流的关系曲线，如图2 所示。

图2 ε=f（I1）曲线

因此，CT 误差又可表示为温度函数

综上可知，CT 误差与其对应各支路一次电流和运行温度密切相关。由式（7）、图2 及式（9）可建立母线差动不平衡电流与其各支路一次电流和运行温度的关联函数，如式（10）所示。

然而，工程实际中并不能直接获取一次采样电流I1i，因此无法建立如式（10）所示的关联函数。但根据电流互感器原理，差动保护各支路一次电流I1i经电流互感器转换为其对应的二次电流I2i，即I1i=NI2i，N 为电流互感器变比。由此，差动不平衡电流可进一步表示为二次电流与运行温度的关联函数，如式（11）所示。

2 差动不平衡电流关联函数拟合

BP 神经网络[12-13]是指基于误差反向传播算法的多层前向神经网络，采用有导师的训练方式。能够以任意精度逼近任何非线性映射，可以学习和自适应未知信卢，构造出来的曲线或函数具有较好的鲁棒性。算法流程：首先初始化网络的结构和权值，然后根据输入样本前向计算BP 网络每层神经元的输入信号和输出信号，根据期望输出计算反向误差，对权值进行修正，如果误差小于给定值或迭代次数超过设定值，结束计算。

采集差动保护系统初始运行时的差动电流与其对应的二次电流和线路运行温度，基于BP 神经网络拟合方法即可得到差动不平衡电流关联函数。

假定某元件G 连接有2 条支路，其差动保护初始运行时二次电流采样幅值分别为Ih21和h22，各支路线路温度分别为Th1和Th2，系统差动电流为Ihcd。设BP 神经网络隐含层有5 个神经元，可得如图3 所示的基于BP神经网络的差动不平衡电流关联函数拟合模型。

图3 不平衡电流关联函数拟合模型

获取采样点k 的差动保护系统各二次电流幅值与其对应线路温度，代入已建立的差动不平衡电流关联函数，即可得采样点k 的差动不平衡电流的拟合值。具体步骤如下。

1）取得原始数据。获取差动保护系统初始运行时差动电流Ihcd及其对应各支路二次电流幅值与线路温度的历史数据Ihcd、Ih2i和Thi。

2）根据BP 神经网络技术要求建立Ihcd关于Ih2i和Thi的关联函数拟合模型。

3）求取b1、b2、b3、b4及b5。将1）中原始数据代入2）中建立模型，利用BP 神经网络算法求得b1、b2、b3、b4及b5，即可得差动不平衡电流关联函数Iunb=φ（I21，…，I2i，…，I2n，T1，…，Ti，…，Tn）。

3 差动保护可靠性评估

比率制动差动保护的通用特性如图4 所示，其中Icd为差动电流，Icdmin为差动电流阈值，Ir为制动电流，Irmin为拐点制动电流值，K 为动作特性曲线l 的斜率。其数学表达式为

图4 差动保护的动作特性曲线

差动保护区外故障时，差动电流阈值Icdmin越大，差动保护可允许较大误差，保护越不容易误动，可靠性越高；但同时差动电流阈值Icdmin越大，也越不容易反映母线内部故障，差动保护灵敏度越低。因此，差动不平衡电流的测量对于其可靠性和灵敏度至关重要。

由1.2 节所建立的差动不平衡电流关联函数，若已知差动保护各连接支路二次电流I2i与其对应运行温度Ti及差动不平衡电流关联函数，便可计算得到差动最大不平衡电流。

通常差动保护设备初始投运阶段，并不存在恶劣的运行环境、绝缘老化及维修等隐藏故障，因此认为此时的差动不平衡电流最能反映差动保护性能。由此，可利用差动保护系统初始运行数据建立如式（11）所示的拟合关联函数。采集差动保护系统某时段的二次电流及其线路运行温度，将其代入所得到的拟合关联函数即可得拟合差动不平衡电流Ifunb，进而得到对应时段母线差动最大不平衡电流的拟合值Ifunbmax。

根据图4 可知，通过比较Ifunbmax与Iunbmax，即可判断母线差动保护系统的可靠性。

1）若最大不平衡差动电流拟合值大于原始值，即Ifunbmax＞Iunbmax；差动保护原始动作特性曲线l 将向上平移到l′处，且处于原差动保护的动作区，实际差动保护装置可能会误动。调整之后将降低母线保护误动的可能性以提升系统的可靠性，有利于系统的安全稳定运行。

2）若最大不平衡差动电流拟合值小于原始值，即Ifunbmax＜Iunbmax；差动保护原始动作特性曲线l 将向下平移到l″处，此时母线差动保护处于制动区，实际差动保护装置可能会拒动。原系统差动电流不变的情况下，Ifunbmax较Iunbmax更小，不但降低了差动保护拒动的概率，提高了系统的可靠性，同时也提升了其灵敏度。

由此，可得到提高母线差动保护可靠性方法的步骤。

1）根据差动保护初始运行数据，建立母线差动不平衡电流关联函数Iund=φ（I21，…，I2i，…，I2n，T1，…，Ti，…，Tn）。

2）获取采样时段t1—t2内差动保护系统的二次电流I2i与运行温度Ti，代入步骤1）所建立的差动不平衡电流关联函数，计算该时段内最大差动不平衡电流拟合值Ifunbmax。

3）比较Ifunbmax和Iunbmax，并调整母线差动电流阈值Icdmin以提高母线差动保护可靠性。

4 结论

电流差动保护对于电力系统至关重要，差动电流阈值的合理性直接关系保护装置能否可靠运行。为此，本文基于BP 神经网络方法建立了差动不平衡电流与其二次电流和运行温度的关联函数，通过调整差动电流阈值进而提高差动保护可靠性。本方法考虑运行环温对电流差动保护可靠性影响，通过实时运行数据可在线评估电流差动保护装置运行可靠性，根据差动不平衡电流拟合值及实际检测情况降低原差动电流阈值，进而防止母线差动保护拒动，具有工程实践应用价值。