统计中的易错题归类剖析

湖北省襄阳市第五中学 王云龙

统计是高中数学中的重要知识,也是高考命题的热点内容。涉及抽样方法、用样本估计总体、变量间的相关关系、回归方程和独立性检验等知识,主要考查同学们的分析数据、处理数据和运算求解等能力。本文剖析了统计中的一些典型易错问题,以飨读者。

题型一、列联表填写有误,导致结果错误

例1研究表明,季节变化引起的光照强度会影响人群的情绪,其主要原因是光照可以控制褪黑素的分泌,干扰正常的生物节律,进而间接参与情绪的调节,为了探究光照强度是否也会影响其他动物褪黑素的分泌,科研人员将200 只小白鼠置于光照条件下,控制光照时长,将光照时长按[0,4),[4,8),[8,12),[12,16),[16,20),[20,24]分组,绘制成如图1所示的频率分布直方图。试验发现,共有130 只小白鼠褪黑素分泌正常,其中光照时长不小于8 h 的有90 只褪黑素分泌正常。

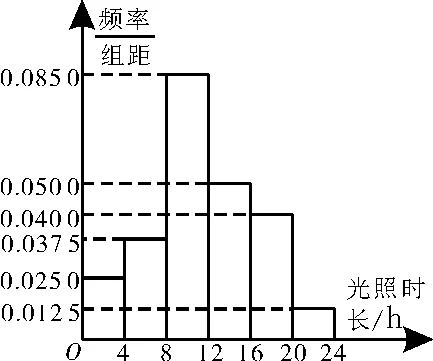
图1

(1)填写表1 所示的2×2 列联表,并根据列联表及α=0.05 的独立性检验,能否认为褪黑素分泌与光照时长不小于8 h 有关联? (单位:只)

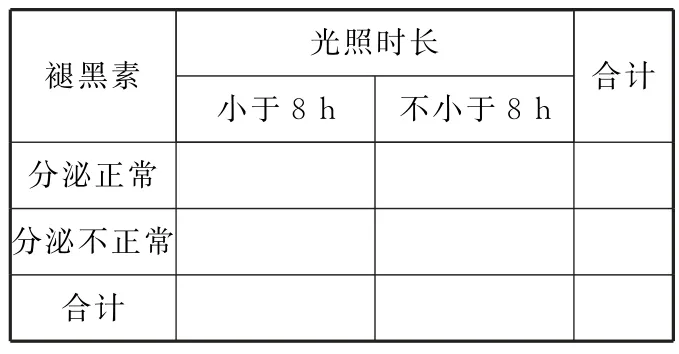
表1

(2)以样本中的频率估计概率,计算光照时长小于8 h 的条件下,小白鼠褪黑素分泌不正常的概率。

表2

解析：(1)(0.037 5+0.025)×4×200=50(只)。

依题设,光照时长小于8 h 的有50 只,不小于8 h 的有150 只,褪黑素分泌正常的有130只,其中光照时长不小于8 h 的有90只,小于8 h 的有40 只,故列联表如表3 所示:

表3

假设H0:褪黑素分泌与光照时长不小于8 h 无关联。根据列联表3 中的数据,得3.841,根据α=0.05 的独立性检验,认为褪黑素分泌与光照时长不小于8 h 有关联,此推断犯错误的概率不超过0.05。

(2)令事件A=“小白鼠光照时长小于8 h”,事件B=“小白鼠褪黑素分泌不正常”,则,所以在光照时长小于8 h 的条件下,小白鼠褪黑素分泌不正常的概率为

易错点剖析：本题容易出现两种错误:①理解题意有困难,2×2列联表的值填写有误,导致计算K2的值出错;②独立性检验思想方法理解不到位,不会找α=0.05 对应的参考数值k0,不能准确解释k0与K2大小关系对应的统计含义。

题型二、相关系数r 不理解,导致模型错误

图2

例2多年来,清华大学电子工程系黄翔东教授团队致力于光谱成像芯片的研究,2022年6 月研制出国际首款实时超光谱成像芯片,相比已有光谱检测技术,实现了从单点光谱仪到超光谱成像芯片的跨越,为制定下一年的研发投入计划,该研发团队为了解年研发资金投入量x(单位:亿元)对年销售额y(单位:亿元)的影响,结合近12年的年研发资金投入量x和年销售额y的数据(i=1,2,…,12),该团队建立了两个模型:①y=α+βx2,②y=eλx+t,其中α,β,λ,t为常数,e为自然对数的底数,对历史数据的初步处理得到散点图,如图2所示,令12),计算得到表4中的数据。

表4

(1)设ui和yi的相关系数为r1,xi和vi的相关系数为r2,请从相关系数的角度,选择一个拟合程度更好的模型。

(2)①根据(1)中的选择及表中数据,建立y关于x的回归方程(系数精确到0.01);

②若下一年销售额y需达到80亿元,预测下一年的研发资金投入量x是多少亿元?

易错点剖析：本题容易出现两种错误:①不理解相关系数r的含义:越接近于1,相关性越强,不会根据相关系数的大小选择回归模型;②非线性回归方程转化为线性回归方程后,不会合理利用参考数据求解模型参数,导致回归方程出错。

题型三、公式运用不合理,导致计算错误

例3重庆轨道交通9号线一期已于2022年1 月25 日开通运营,全长32.29 公里,从高滩岩站至兴科大道站,一路经过23座车站。沙坪坝站是目前客流量最大的站点,某数学兴趣小组在沙坪坝站做乘客流量来源地相关调查,从上车人群中随机选取了100名乘客,记录了他们从来源地到沙坪坝站所花费时间t,得到表5:

表5

(1)估计所有在沙坪坝站上车的乘客花费时间t的中位数。

(2)已知t∈［0,6）的6 人,其平均数和方差分别为5和1.5;t∈［6,12）的30人,其平均数和方差分别为8和9。请计算样本数据中t∈［0,12）的平均数和方差。

总之,熟练掌握数据统计方法,深刻理解统计方法的含义,可以让我们在学习统计的过程中更加游刃有余。