数学文化视角下序言课的教学设计探讨*
——以高中“微积分”为例
湖北省黄冈市黄冈师范学院(438000) 华永莲 马晟 张莹莹
1 引言
《普通高中数学课程标准(2017年版2020年修订)》(以下简称课标)中提出:数学文化应融入数学教学活动[1].这无疑确立了中国数学课堂,文化教学的课程形态.教师应有意识地结合相应教学内容,将数学文化渗透在日常教学中,引导学生了解数学的发展历程,认识数学在科学技术、社会发展中的作用,感悟数学的价值,提升学生的科学精神、应用意识和人文素养[1],这为数学教师文化教学指明了实践方向.将数学文化融入教学,还有利于激发学生的数学学习兴趣,有利于学生进一步理解数学,有利于开拓学生视野、提升数学学科核心素养[1],更向我们阐明了数学文化所具有的深厚的文化育人的功能和价值.为此,数学文化教学课例、策略等的探讨研究应时而生.其中,关于微积分的教学设计与教学对策多以新授课内容为例展开研究[2-5].由此可知,知识的学术形态转化为教育形态重在教学设计,即“备好课”是上好课的关键.也有学者以学习理论为导向探讨建构主义与学习迁移理论在大学微积分教学中的应用策略[6-7].情境认知学习理论在数学教学中的应用研究相继出现[8].可见,适当的应用学习理论是提高课堂效率的必要武器.由此提出,以学习理论为指导,融入数学文化进行教学设计是提升数学学科核心素养的重要落脚点.
《课标》建议抓住内容主线,引导学生从整体上把握课程[1].显然,序言课是很好的突破口,但因课时紧张,大多数教师并不重视序言课教学.查阅发现对序言课的教学研究也是廖若星辰.可见,对序言课的重视度还不够高.序言课是数学教育领域中较为新颖的一个研究方向,序言课的学习是为了促进新知识的学习,具有先行组织者的作用[9].由此,本文以情境认知学习理论为指导,选择令学生头疼的微积分内容,融入数学文化,以史为线展开微积分序言课教学设计,以期在所谓的浪费时间的教学中,抓微积分内容主线落实立德树人、提升素养的基本育人理念.
2 情境认知学习理论的主要观点及教学启示
以下将从理论主要观点和教学启示两方面阐明其对本文的指导.
2.1 主要观点
情境认知理论的核心观点是活学活用、知识来自于活动;主张将关注的焦点从学习者本身转到整个学习所处的情境脉络以及其中的学习活动.
2.2 教学启示
首先,数学知识应根植于情景脉络之中.按照情境认知理论,任何数学理论都有其产生的现实背景.本文引领学生大致经历微积分的发展历程,使学生对微积分的认识根植于情境脉络中,感受其文化价值.其次,通过运用来理解数学.按情境认知理论,数学知识既是境域的,又是通过活动和运用不断发展的.本文设计行李箱优化问题、物理运动问题等,使学生在生活、自然中把握微积分的本质,领会微积分的思想基石.最后,数学学习是一个文化浸润的过程.按情境认知理论,教师要关注环境文化对学生的影响.本文借助多媒体创设趣味问题情境、科技情境,启发学生思考,拓宽其视野,改善数学学习.
3 序言课教学设计
3.1 设计理念
序言课大致分为三类:知识层面、方法层面、文化层面[9].本课设计将在数学文化视野下,选取微积分发展过程中的重大事件与关键人物,以史为轴线,并以情境认知理论为指导,在师生双边互动的情境脉络中开启微积分的历史画卷,突出微积分内容主线.使学生体验微积分学的核心思想,探索微积分的实质,落实立德树人、提升素养的基本理念.
3.2 基于数学文化的微积分序言课教学设计
整个教学过程通过四步走环节使学生自决钻研本章序言课三大核心问题:为什么学微积分? 学什么内容? 怎么去学微积分?
3.2.1 问题导入-发人深思-感知极限
问题1惠子(公元前370-前310年)曰:“一尺之棰,日取其半,万世不竭”,你怎样看?
问题2芝诺悖论(Zeno 约公元前5世纪)——希腊神话中的英雄阿喀琉斯追不上乌龟吗? (乌龟起点靠前100 米)
设计理由以中西方哲人的名言与悖论作为问题导入,创设趣味性问题情境,使学生以数学的眼光与现实的角度解答以上问题,自然一千个读者的心中有一千个哈姆雷特,不同的学生会有不同的回答.由此,学生产生思维碰撞,使课堂气氛达到一种“愤”的状态,此所谓不愤不启,教师顺利引出微积分的历史起源.使学生感受无限寓于有限之中,二者既对立又统一,培养学生辩证唯物主义的世界观与方法论.
3.2.2 历史探源-理清脉络-领会实质
问题3回顾小学探究圆面积的过程,总结我们曾收获的思想方法.
引入史料中国古代刘徽(公元225-295年) 的割圆术——如刘徽所言“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.可见刘徽的极限思想并未受到无限的困扰,并不断倍增圆内接正多边形的边数,逐步逼近圆为求圆周率的方法.以此思路刘徽坚持算到了正3072边形,由此计算出圆周率在3.1415 和3.1416 之间.两个世纪后祖冲之将刘徽的方法用于24576 边形,最终将圆周率的虎钳收紧至3.1415926 与3.1415927 之间,领先西方一千一百多年.
设计理由问题3 是小学六年级内容,学生在回顾中再次感受无限分割近似求和的思想方法.借此引出知识源流——割圆术,体会其中蕴含的微积分最初的极限思想.再者,祖冲之计算圆周率的刻苦求实、坚忍不拔都是我们孜孜以求的.进而,弘扬中华文化,增强名族自豪感,树立文化自信,培养学生的爱国主义情操.
问题4类比求圆面积“无限分割”的思想,请尝试求抛物线弓形面积,如图1.
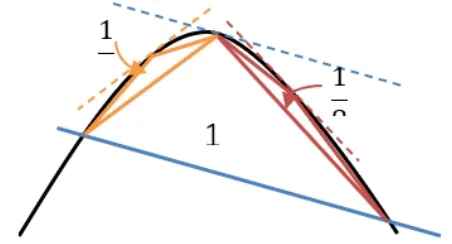
图1
引入史料古希腊数学家阿基米德(公元前287-前212年) 最早使用穷竭法进行了积分运算.首先他为碎片化内接三角形建立了一致模型,如图1.即每一级内接三角形的顶点是其底边的平行线与抛物线的交点.随后阿基米德证明了每个新层级的三角形面积是上一级的1/8.最后给这无穷层级的三角形进行面积求和.假设一级内接三角形面积为单位1.
则:所以:4S=求得:
紧接着,阿基米德通过双重归谬法(双重反证法) 对此前结论进行了严格论证,即弓形面积不可能小于4/3 或大于4/3,因此只能等于4/3.此论证过程是建立在有限内接三角形的基础上展开的,它避免了无穷,故他的证明无懈可击,也是对穷竭法的进一步完善.阿基米德并将其广泛应用于求解曲面面积和旋转体体积,是微积分学的先驱.
设计理由首先,斯宾塞、波利亚以及克莱因等人相信种族的发展积淀为个体的发展,个体知识的发生遵循人类知识的发生过程,即历史发生原理[10].故遵循历史先积后微的发展顺序设置此问题.其次,根据维果斯基的“最近发展区”理论,适当拔高难度.学生即使不能完全求解问题4,也会有一种无限分割、近似求和的数学思想在脑海中浮现.此时引出阿基米德在《抛物线求积法》中求解抛物线弓型面积的策略.在此使学生进一步领会微分即无限细分弓形面积,积分即求无穷内接三角形面积之和.
问题5请设计一款行李箱,宽和深均为x,且长宽高之和不超过45.猜一猜x为何值时行李箱容积最大呢? 该怎么求解呢? (如图2,直线向上滑动,最大值处两点合并为一点)
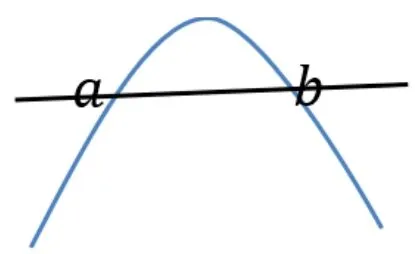
图2
因:V=x·x·(45−2x),由:V(a)=V(b),即:45a2−2a3=45b2−2b3,化简得:45(a+b)(a−b)=2(a2+ab+b2)(a−b),令:a≈ b,90a=6a2,求得:a=0,a=15.
引入史料到17世纪20年代末,费马借助重交点概念,几乎找到了所有代数曲线(只能用x和y的整数次幂来表示)的切线.相继,笛卡尔在1637年出版的《几何学》中公布了他求切线的方法(用圆去横穿曲线找到重交点)[11].而后,费马徒手算出了曲线y=xn(n ∈N+)下方的面积.遗憾的是他们至此都未发现求曲线下方面积和曲线以及曲线的切线之间蕴藏的秘密.笛卡尔也不知道他创造的xy平面这个十字路口,使方程与曲线、代数与几何、东西方数学都在此相遇意味着什么.直到牛顿和莱布尼茨的登场,他们站在前人的肩膀上将彻底统一微分学与积分学.
设计理由此题改编自费马设计的优化问题,使学生先猜测后分析.学生可以通过小组合作,尝试不同设计,猜测出立方体15×15×15 设计似乎使箱子容量最大,这种猜测并不具有一般性,但这种猜测可以激发学生对未知知识的探求兴趣.而后学生列出方程,根据提示分析求解.最后向学生说明刚才所用的代数分析法就是费马曾解决此类优化问题用过的,并引入史料说明解析几何的诞生和求切线问题为微分学的发展开辟了道路.使学生明白,伟大的微积分的诞生,是古今中外历代科学家心血和智慧的凝聚,并不是某一个人的成就.
问题6请根据以下图像探究问题.
(1)图3、4 中的路程与图形面积有何关系?
(2)图3、4 中面积(由(1)可知面积是路程)的变化率与速度有何关系呢?
(3)图3、4 中速度的变化率(加速度)与直线的斜率有何关系呢?
(4)图3、4 若是曲线,猜想以上关系还成立吗?
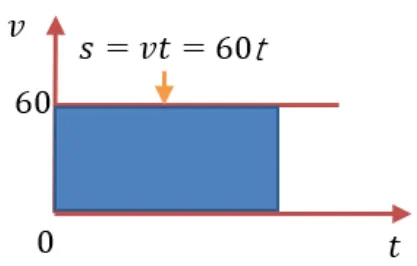
图3

图4
师生探究发现以下关系:
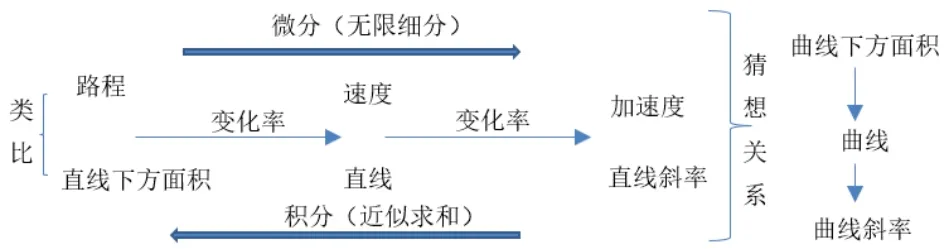
引入史料1艾萨克·牛顿出生于1642年的圣诞节.16岁时,母亲让他离开学校并强迫他经营家庭农场,他讨厌农活,最终在家人的劝说下母亲同意他回到学校.1664-1665年冬天,牛顿受沃利斯的《无穷级数》一书中求曲线下方面积新方法[11]的影响,即把复杂形状想象成简单形状的无穷级数之和.通过类比,对新方法进行改进升级,用符号代替形状.就这样,年仅22 的牛顿能用幂级数表示出任何曲线或函数,找到了求任意曲线下方面积的系统方法.到1671年牛顿已统一了微积分的各个部分,并将其扩充为《流数术与无穷级数》.这本著作在他有生之年并未公开发表,直到1736年才出版[11].
引入史料2莱布尼茨身为外交官、逻辑学家、语言学家和哲学家的他发现微积分的方法与牛顿正好相反.在求无穷级数(如1/(1×2)+1/(2×3)+···+1/n(n+1)+···)的和时,他把特殊结构的和改写成连续差之和的形式,因此出现大规模抵消,最终问题得到解决.这让他想到了把曲线下方面积分成很多竖直的矩形[11],就好比很多连续的数,那么求很多竖直矩形面积的和不就类似于求许多连续的数之和,中间也会出现大规模抵消.最终,在1672-1676年他创立了自己的微积分.虽然莱布尼茨发现微积分晚于牛顿,但由于他创造的微积分易于理解,并且他用一套简洁的符号表示微积分并于1686年率先发表,因此人们都认为他也是微积分的发明者[11].
设计理由问题6 中的运动现象是学生高一年级物理中学过的,对此学生很清楚速度是距离的变化率,加速度是速度的变化率.通过类比使学生把运动关系与几何关系建立联系,从而推出面积、直线与直线斜率三者间的关系,并说明以上过程正向推理是微分,反向推理是积分,这便构成微积分的两大部分,再从推理结果对任意曲线下方面积、曲线与曲线斜率三者关系进行猜想.此环节联系物理学科,通过类比、猜想使微积分思想方法浮出水面.此种设计是为凸显数学的学科交融性与科学价值,且在一定程度上留给学生猜想与探索的空间.最后,介绍牛顿和莱布尼茨发现微积分的方法不同,但他们的相同点在于对知识的迁移与类比,牛顿由形到数,莱布尼茨由数到形,他们大胆的类比与迁移的思想方法与深邃的智慧都是我们前进道路上值得珍视的.
3.2.3 科技力量-拓宽视野-着眼未来
课堂接近尾声,教师借助多媒体与精简的语言让学生体验科技情境.
科技情境计算机动画之与微积分——动画师通过反复分割平面,用几万个甚至几十万个多边形创造出我们喜欢的动画卡通人物.细分程度越高,动画越逼真,所占用内存越少.这无不体现了阿基米德的洞见:任何平滑表面都可以令人信服地用三角形来逼近[11].
设计理由顺应《课标》建议:引导学生认识数学在科学技术、社会发展中的作用,感悟数学的价值,提升学生的科学精神、应用意识[1].通过以上情境,使学生感受“在互联网+”时代,微积分不仅是一种数学符号语言,更是一种强大的科技工具.放眼当下,师者传道授业解惑也,放眼未来,必为学生之未来负责.因此,在这里展示科技情境不单是为拓宽学生视野,更是让学生透过科技情境看到微积分的力量,让学生着眼于未来思考微积分的价值.
3.2.4 核心三问-内化于心-外化于行
课后作业思考我们为什么学微积分? 我们能学到什么? 在此过程中我们该怎么学呢?
设计理由《课标》建议:丰富作业形式,提高作业质量,提升学生完成作业的自主性、有效性[1].以序言课的核心三问为课后作业,不同的学生有不同的出发点、孕育点和落脚点.不是老师告诉学生“我”为什么而学、“我”学到了什么、“我”要怎么学,而是通过以上问题情境、历史脉络、科技情境为指引,引导学生独立思考本节课的核心三问,留给学生独立探索的空间,从而使学生对微积分的伟大思想有所内化,那么每个学生必定都有自己的一本蓝图,这样在接下来的学习中才会自决钻研,即内化于心,外化于行.
4 结论
本文以数学文化为线,以情境认知理论为指导,创设相关情境脉络.设计重“廓”,即微积分核心思想的凝练与本质的归纳,而不是具体内容的讲解.其中,引入中国惠子名言与古希腊芝诺悖论,是引领学生初步感悟极限思想,也让学生辩证的看待有限与无限,二者即对立又统一.引入知识源流,如刘徽的割圆术、祖冲之与圆周率等,是为引领学生弘扬中华文化,增强民族自豪感,树立文化自信,在此可以毫不夸张的说祖冲之将圆周率的虎钳收紧至8 位数,绝对称得上人类史上的壮举.设计匀速直线运动与自由落体运动问题,是为学生方便推理面积、直线、直线斜率三者间关系的同时,也为学生展示自然运动拥有数学的内核.介绍计算机动画之与微积分,意在向学生展示微积分在影视艺术等领域的科技力量,不单为拓宽学生视野,更是让学生体会到应用这种科技工具于人类而言是多么令人兴奋与惊叹的事,使学生不仅仅局限于现在的学习,更是放眼于未来的发展.
作为一名数学工作者所期望的是,我们该引领我们的学生站在前人的肩膀上,在生活中、在自然中发现纯粹数学领域中的微积分,在初步理解微积分的前提下,尝试着用微积分语言去描述周围世界,在掌握更多相关知识后,努力用微积分者(理解微积分的人)特有的眼光观察世界,在完全掌握微积分的思想方法后,用微积分这个强大的科技工具去改造世界.

