基于多数据融合+BP 神经网络的农业温室大棚环境监控系统的研究

许德立, 皇甫森森, 李澍源

（1.福建农林大学金山学院, 福州 350002；2.厦门大学嘉庚学院, 福建 漳州 363105；3.福建师范大学后勤管理处, 福州 350117）

在现代农业温室大棚中, 温室内环境对经济作物发展非常重要。由于温室内环境主要与温室植物的生长发育、植物有机质的吸收与能量转换等有关, 所以有必要对温室的环境加以严格监控, 以保证温室一直保持在最适宜于经济作物生长发育的环境[1］。因此, 为了促进温室农业技术的发展、创新和优化生产设备, 提高农产品质量和生产效率, 实现科学生产、合理产业化和高效实现大棚作物的高产, 有必要开发大棚农产品生产的软硬件技术以及主要系统和硬件[2］, 将更恰当的控制策略和自动化产品应用于农业生产, 以保障温室作物适宜的气候条件[3］。

目前, 中国科技发展水平不断提高, 人们对现代农业智能化水平的要求也不断提高, 利用智能化方式实现农业温室大棚的气温调节、相对湿度调节、水肥灌溉等。但如何能有效地实时监测农业温室大棚环境, 并作出正确的控制策略是一直存在的问题, 也在不断地改善。目前只有少数智能温室监控系统运用于中国的温室生产[2］。温室环境控制工程技术是一项非常全新的农业种植技术, 通过该项技术可以实时地对农业种植过程中各类环境参数的变化进行监测[2］, 根据监测情况采取必要的措施, 保证农业大棚环境处于植株适合生长的环境, 使作物在最佳自然环境条件下正常生长, 并能更好地提高产量[3］。

目前, 中国已在温室监测和控制等领域开展了若干探索与实践, 常见的智能温室大棚属于简单的智能监控系统, 它是依靠大棚内单一类型传感器数据采集后的环境参数作为调节控制的依据, 这样就会存在调节控制力度不够或者调节过度的问题[1］。针对上述问题, 有必要研究一种基于多数据融合+BP 神经网络的农业温室大棚监控系统。在大棚内部分布多点传感器, 避免了单个传感器测量不准确的问题, 通过加权平均算法进行数据融合, 再结合BP 神经网络对参数的变化趋势进行判断, 最终得到决策后的控制策略。通过多数据融合+BP 神经网络预测的方法, 实现更为精准的大棚环境参数的预测, 同一类型多个传感器监测的多个数据进行融合后所获得的参数（如相对湿度、温度、二氧化碳浓度等）, 相比单一传感器监测得到的数据更为准确, 对融合后的测量数据再加以神经网络的训练, 获得各参数变化的趋势, 为良好的大棚种植环境提供保证[3］。

1 系统总体框架

农业温室大棚系统架构如图1 所示, 系统架构分为多点传感器数据采集层、数据融合层、BP 神经网络全局融合层3 个层级。

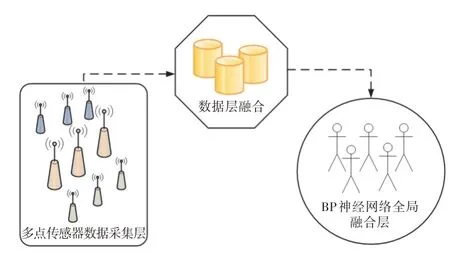
图1 农业温室大棚系统架构

根据温室大棚需要采集的不同类型参数, 采用不同的传感器, 首先, 通过多点布置让传感网中的数据采集层获得不同环境参数集[4］；其次, 进行数据融合, 滤除异常部分以获得准确数据[5］；最后, 将数据融合后的多个类型数据参数（如温度、相对湿度）作为BP 神经网络输入, 进行各参数变化趋势的预测, 得到最终的控制策略[6］。

2 农业温室大棚环境监测系统数据融合模型

数据的处理和应用是农业温室大棚环境监控最重要的部分, 得到精准的参数数据以及参数变化趋势, 以此为依据对温室大棚内各项自动控制设备的调控具有非常重要的指导意义。温室大棚环境中参数有很多, 如温度、相对湿度、光照度等, 每个参数都需要经过多个传感器采集, 并对数据进行处理, 才能得到有效的控制数据[5］。本研究以温室大棚环境的温度和相对湿度2 个参数作为该系统的研究对象, 研究温室大棚的监控情况, 建立基于多传感器数据融合技术的2 个层级的融合模型, 农业温室大棚环境监测系统数据融合模型如图2 所示。

图2 农业温室大棚环境监测系统数据融合模型

农业温室大棚监控系统采用2 个层级的融合数据, 第一级是数据融合层, 是将传感网中获取的数据集作为数据融合层的输入（即一级融合）, 该级融合层是应用了自适应加权融合算法, 对本温室大棚中的温度和相对湿度数据集进行处理。第二级是神经网络融合层, 将数据融合层得到的温度、相对湿度作为该级的原始数据, 采用BP 神经网络算法进行融合, 从而提高温室大棚环境监测的可靠性。

3 结果与分析

3.1 多点传感器数据融合

3.1.1 加权平均数据融合算法 加权平均融合算法在许多研究中已经被证明是一种较为成熟的融合算法, 该方法能实时处理动态的原始数据。加权平均融合算法可以提高系统的精度、测量范围以及增加系统的可信度[6］。

在温室大棚中对某一参数（如温度）, 利用n个传感器进行温度数据的采集, 采集到的温度数据集利用加权平均融合算法处理。

对某个温度传感设备i, 在时刻k进行状态估计, 且相互间的估计误差互不相关, 其所在的局部状态估计值表示为, 假定其为无偏估计[5, 6］。

v1,v2,…,vn为各传感设备的权重, 可得到和vi的关系式：

加权平均融合算法使v1,v2,…,vn的值相近, 根据公式（1）,, 如公式（2）所示,就是经过融合后的状态估计值。

3.1.2 自适应加权融合算法与应用 在数据的采集过程中, 由于测量目标存在随机干扰和传感器本身性能的差异, 各传感器的实际测量值必定会有所偏差, 这就会导致本系统在一级融合层开始就会产生偏差。所以各传感设备需要采集多个测量值, 采用自适应加权算法, 可以在不需要先验知识的情况下直接对其有效处理[6］。所以, 本系统参数的多点数据融合采用自适应融合算法能有效将产生的偏差减小, 以获得较为准确的环境参数, 保证获取的温度、相对湿度数据位于尽可能小的偏差范围。

1）算法模型。本系统中的各环境参数都有多个传感器位于不同监测点, 若传感器个数为n,X1,X2,…,Xn分别为这些传感器采集到的数据。

在保证总方差最小的条件下, 对X1,X2,…,Xn进行加权融合, 通过自适应的方式寻找对应的最优加权因子, 经过该方式得到融合后的最优值。本温室大棚系统的自适应加权算法模型如图3 所示。

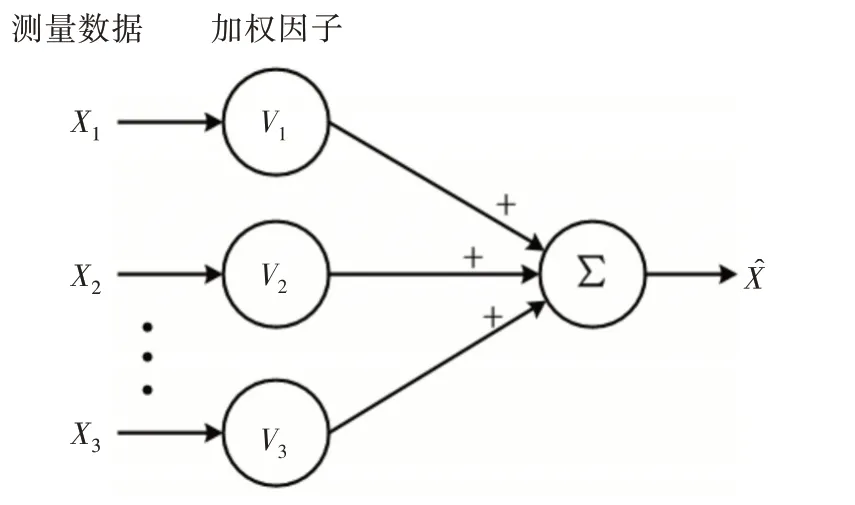
图3 自适应加权算法数据融合模型

2）原理分析。根据上述算法模型分析, 本系统采集某个参数的传感节点数为n, 对应各节点的方差为不同设备采集数据相互独立, 认为其属于估计真值X的无偏估计值[6, 7］。公式如下：

总均方误差为：

由于X1,X2,…,Xn两两之间是相互独立状态, 又是属于X的无偏估计, 故有：

由公式（6）可知,σ2的值和精度的高低成反比, 因此, 求其最小值就可以保证所得参数的准确度, 且σ2取得极值的情况与每个传感器的V相关[5-7］。

当系统参数数据经过上述处理后, 得到最小均方误差, 由多元极值理论得到V, 计算公式如下：

已知温室大棚内某个参数的各点传感器某时刻的测量值, 且X为常量。这是作为上述估计的必要条件, 此时可得到精确度较高的估计值。

对上述的某个p传感器进行监测采样, 共取得k个数据, 求得p传感器的均值为：

同理可得：

当σ2最小时对应的符合精度要求, 此时最小值为：

3.1.3 自适应加权融合算法仿真 温度和相对湿度采样次数为5、10、30 次, 自适应加权算法以及算术平均值算法后的均值与均方值如表1 所示。当采样次数为10 次时, 在本系统中融合效果最好。结果表明, 自适应加权算法相较于传统的算术平均值算法具有高融合度和精度, 但采样次数需要根据不同系统进行相应调节, 一般不大于30 次为最佳。

表1 不同采样次数的自适应加权算法以及算术平均值算法均值与均方值

图4 为算术平均值算法和自适应加权算法温度、相对湿度数据融合对比图, 温度真实值为23 ℃, 相对湿度真实值为75%。采用自适应加权算法进行数据融合可以有效地得到接近真实值的融合数据, 而采用普通的算术平均值算法可能因为存在异常值, 导致数据在某个时刻由于异常数据过大或过小, 使融合后数据偏离真实值较远。所以, 采用自适应加权算法融合后的数据更为准确, 提升了BP 神经网络输入数据的可靠性。

图4 算术平均值算法和自适应加权算法温度、相对湿度数据融合对比

3.2 BP 神经网络数据融合

3.2.1 BP 网络设计 BP 神经网络是一种前向型网络, 它可以将得到的误差反馈后进行修正[8］。这种模型基本结构为输入层、隐含层、输出层, 故需要对其基本结构中所包括的网络层数、各层节点个数、网络初始权值、学习速率提前进行设计[9-12］。

1）网络的层数。输入层和输出层是神经网络中必须具备的, 而隐含层是根据需要对其层数进行确定；需要注意的是网络误差的高低与对应层数成反比、与系统精度高低成正比, 若增加对应层虽然可以使系统预测更加精准, 但其整体结构也更加复杂。在综合考量后, 本系统采用3 层隐含层结构的BP 神经网络, 可实现任意的n维到m维的映射。

2）各层的节点数。输入层和输出层的选择都是根据实际应用要求决定的, 本研究的全局融合中心是以温度和相对湿度作为输入变量, 即温度、相对湿度2 个参数作为输入层的2 个节点。对神经网络来说, 其性能的好坏、预测精准度的高低在一定程度上是受隐含层节点数多少的制约, 如何获得合适的节点数, 通常需要根据不同的系统特性进行测试或依据先前的经验来确定[10-13］。根据经验可以参照以下公式进行设计：

式中,L为隐含层节点数；n为输入节点数；m为输出节点数, 输出层节点数根据实际应用选择；a为常数, 取值范围为a∈[1,10]。

由于温度、相对湿度对农作物的生长具有重要的影响, 一个合适的温度和相对湿度调节区间能保证植株的生长环境处于较好的生长条件下。本系统输出信息包括最适宜、适中、恶劣, 因此这3 种状态即为本系统所确定的输出层节点。根据公式（14）, 本系统确定L为4。本系统温室大棚的环境舒适等级分为3 级, 级别越高说明所处的环境越适宜。等级划分如表2 所示, 0 级表示环境较为恶劣, 需要及时做出调整；1 级表示环境较为舒适, 暂无须调整；2 级表示环境最适宜, 有助于农作物生长。

表2 农业温室大棚环境等级划分

3）网络的初始权值。BP 网络中隐含层的传输函数通常采用S 型传递函数, 本系统在该初值的选取时应保证不能偏大, 且本温室大棚神经网络系统选取连接权值为不在同一时刻相等的某一随机数, 其区间位于[-1,1]。

4）学习速率。学习速率如果选得太小, 则收敛慢, 网络训练时间增加；如果学习速率过大, 会导致网络稳定性降低。综合考虑, 本系统选取的学习速率η为0.01。图5 为确定了网络层数以及各层节点数后的温室大棚BP 神经网络结构。

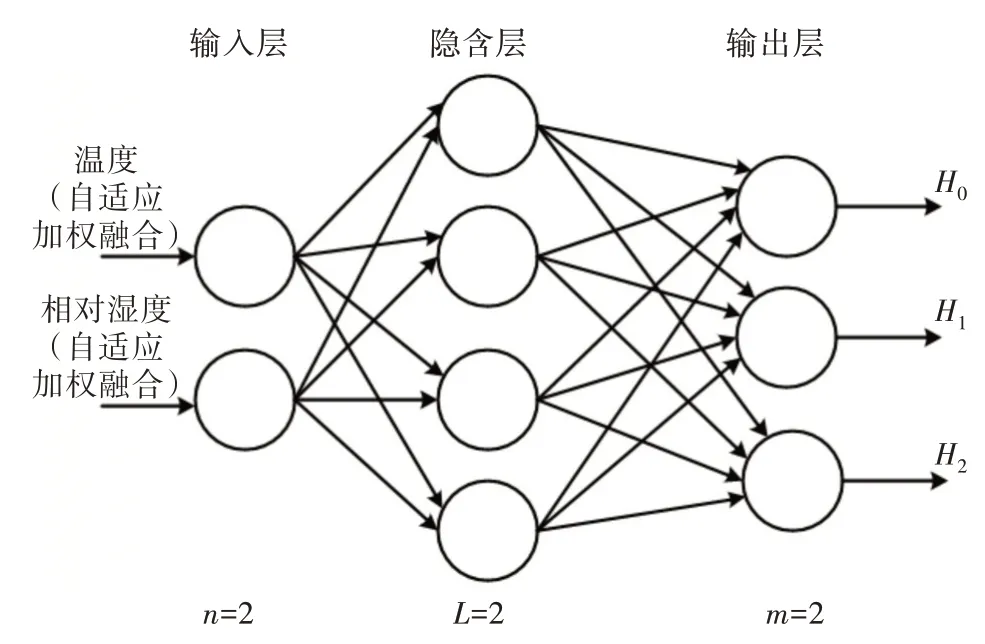
图5 农业大棚BP 神经网络结构

3.2.2 BP 网络模拟测试结果 本系统BP 神经网络训练样本数据的选取, 采用重要数据样点的选取方法, 这样避免了无效数据, 同时可以重点针对重要数据训练, 使训练效果更好, 本系统选取温度、相对湿度传感器的3 个数据样本。由图6 可知, 当训练次数为1 时, 预测准确率在73%左右, 训练次数增加到50 次时, 预测准确率提高到85%左右, 当训练次数增加到200 次及以上时, 准确率基本维持在98%左右。由于初始数据已经经过自适应加权融合, 在训练次数为1 次时, 训练预测准确率也可以达到70%左右, 可见在BP 神经网络输入前对数据进行融合处理, 可以较好地提升预测的最低准确率。

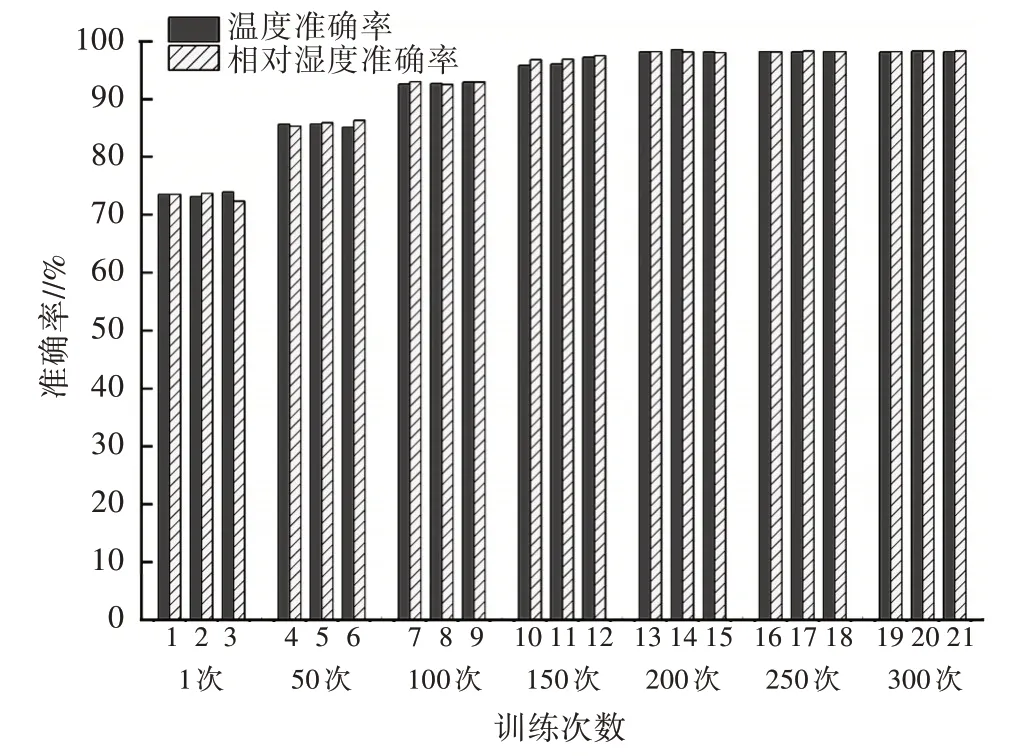
图6 BP 神经网络的预测准确率

4 小结

在农业温室大棚的智能监控和管理工作中, 智能控制技术的运用对于改善生产管理水平和产品质量有一定的指导作用。通过利用智能控制的优势, 克服传统温室监控的技术缺陷, 能够完成对温室内智能监控与管理工作, 从而提高农业植物的生产现代化、自动化与智能化。

本研究阐述了在农业温室大棚内利用多传感器对不同点位传感器监测数据进行采集。第一级数据融合层将传感网中获取的参数数据集作为数据融合层的输入, 该级融合层是针对本农业温室大棚中的温湿数据集, 应用自适应加权融合算法对多点数据进行处理。第二级是神经网络融合层, 将数据融合层得到的温度、相对湿度作为该级的原始数据, 采用BP 神经网络算法进行融合, 进而对环境优劣情况进行预测。