基于可满足性模理论的虚拟网映射问题求解

余建军 吴春明

1(衢州职业技术学院信息工程学院 浙江 衢州 324000) 2(浙江大学计算机科学与技术学院 浙江 杭州310027)

0 引 言

网络虚拟化技术作为解决互联网僵化问题的关键技术，正成为云计算范式的核心技术。虚拟网映射[1]是网络虚拟化技术的核心问题，其任务是当单个虚拟网络构建请求动态到达后，构建该虚拟网络的映射方案并完成映射。单个虚拟网映射问题是NP难问题[2-3]，求解该问题的精确算法具有非多项式时间复杂度，故当前提出的单个虚拟网映射算法主要集中在启发式算法[2,4-7]，当然也有少数单个虚拟网映射问题的精确算法被提出，因为精确算法设计对启发式算法设计具有启发意义，且精确算法可用于中小规模问题求解以及启发式算法的性能评估。精确算法可以分为两阶段映射精确算法和一阶段映射精确算法两类[8]。

两阶段映射精确算法采用迭代技术，每次迭代都是在完成虚拟节点映射后进行虚拟链路映射，迭代的依据是虚拟网映射方案的目标函数。文献[9]以映射代价最小化为目标，建立了基于路径的单个虚拟网映射问题的混合整数规划模型P-VNE；在分析P-VNE模型的对偶规划模型的基础上，提出了求解单个虚拟网映射问题最优解的嵌入于分支限界搜索框架下的列生成算法。文献[10]以最小化物理网络资源消耗为目标，通过增强文献[9]的P-VNE模型，建立了基于路径的单个虚拟网映射问题的混合整数规划模型，并基于该模型设计了两阶段映射精确算法。该算法的主要流程如下：① 首先假设部分物理节点已经被虚拟节点所映射；② 基于虚拟网络拓扑结构进行虚拟链路映射，从而形成MILP模型新的约束条件，并得到该虚拟网映射问题的上届；③ 假设虚拟链路已经完成映射，然后完成虚拟节点映射，从而形成MILP模型新的约束条件，并得到该虚拟网映射问题的下届；④ 重复步骤①、②和③，直到虚拟网映射问题的下届等于或接近等于上届。

一阶段映射精确算法是指虚拟节点映射和虚拟链路映射同时进行的精确算法。一阶段映射精确算法是通过建立单个虚拟网映射问题的数学规划模型，然后通过分枝定界法、整数规划算法等常用方法求解。文献[11]以最小化物理网络资源消耗和负载均衡为目标，建立了基于节点-链路的单个虚拟网映射问题的整数线性规划模型，并采用优化软件CPLEX求解该模型，该模型的约束条件包括了链路延迟约束和虚拟节点最大距离约束。文献[12]针对小规模的单个虚拟网映射问题，以映射代价最小化为目标建立数学规划模型，并用优化软件LINGO来求解。

虚拟网映射问题精确算法设计的关键是提高其求解效率，目前所提出的一阶段映射精确算法是基于求解数学规划模型的优化软件来实现的，其求解效率有待进一步提高，以进一步增强其实用性。鉴于可满足性模理论在线性逻辑约束公式优化问题求解领域有突出优势[13]，本文基于可满足性模理论，设计了虚拟网映射问题一阶段映射精确算法，并通过实验对比和分析，验证本文方法的有效性。具体而言，针对物理网络不支持路径分割且物理节点不支持重复映射的虚拟网映射问题[2]，首先建立以物理网络资源消耗量最小化为目标的单个虚拟网映射问题的整数线性规划模型；然后，基于可满足性模理论[13]提出了一种解决物理网络不支持路径分割且物理节点不支持重复映射的虚拟网映射问题的精确求解方法。

1 问题描述和数学模型

1.1 问题描述

1.2 虚拟网映射收益及目标

虚拟网映射问题是在线优化问题，其求解目标往往是多样化的[2]，如从物理网络提供商的角度，其目标是最大化长期收益；从服务提供商的角度，其目标是最小化从物理网络提供商租用的资源量；其他还有节能、安全、容错等[14]，本文以最大化物理网络提供商长期收益为其映射目标。在单个虚拟网映射时，因其收益是常数，为达到长期映射目标，最小化映射成本是单个虚拟网映射问题的主要目标[2]，本文将物理网络资源(CPU容量和物理链路带宽)消耗量定义为映射成本[10,12]。

1.3 整数线性规划模型

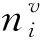
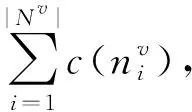
(1)

(3) 约束条件为：

(2)

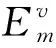
(3)

(4)

(5)

(6)

式中：si和ti是第i条虚拟链路的两个端点对应的源节点，式(4)、式(5)和式(6)表示流守恒，即除了源节点si和目标节点ti外其他节点的网络净流量为0。

(7)

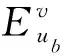
(8)

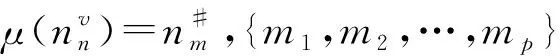
(9)

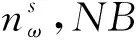
式(9)确保每个物理节点最多只能被一个虚拟节点所映射。

2 基于可满足性模理论求解器的虚拟网映射问题求解

2.1 虚拟网映射问题的SMT公式

命题逻辑可满足性问题(SATISFIABILITY，SAT)[13]是NPC问题，SAT技术被广泛应用于自动电子设计、静态程序分析、测试用例生成等领域。针对SAT存在只面向命题逻辑公式、表达能力有限等问题，人们将SAT扩展为可满足性模理论(satisfiability module theories，SMT)[13]。SMT是判定一阶逻辑公式在组合背景理论下的可满足性问题，SMT技术在测试用例自动生成、线性逻辑约束公式优化问题求解等领域有突出优势。

通过构建虚拟网映射问题的SMT公式VNM_SMT，从而将虚拟网映射问题建模为线性逻辑约束求解优化问题。虚拟网映射问题的SMT公式由式(10)-式(19)组成。

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

蕴涵词用⊃表示，A⊃B等价于A∨B。式(10)确保物理节点剩余CPU容量大于等于映射到该物理节点的虚拟节点的CPU容量需求。式(11)确保任意物理链路上所映射的所有虚拟链路带宽之和小于等于该物理链路的剩余带宽。式(12)确保源节点不能成为流的中间节点。式(13)、式(14)和式(15)表示流守恒，除了si对应的源节点和ti对应的目标节点外其他节点的网络净流量为0。式(16)确保每个源节点(对应虚拟节点)只能映射到唯一的一个物理节点上。式(17)确保每个物理节点最多只能被一个虚拟节点所映射。式(18)表示优化目标是最小化物理链路带宽消耗量。

2.2 基于SMT求解器的虚拟网映射问题求解

2.2.1SMT求解器

用以求解SMT问题的自动化工具称为SMT求解器。SMT求解器的算法实现分为两类，第一类是积极类算法，它将SMT公式转化为SAT公式，然后用SAT求解器求解；第二类是惰性算法，它将SMT公式层次化为布尔公式与理论公式，然后采用SAT求解器与理论求解器互动求解[13]。

积极类算法将SMT公式转化为SAT公式时，SAT公式长度随问题规模呈指数型增长，故不适用于大规模问题求解。而惰性算法通过SAT求解器与理论求解器互相配合，提高了问题求解效率，成为大多数SMT求解器的选择。

目前，主流SMT求解器支持的背景理论有整数集上的线性算数理论(quantifier free_linear integer arithmetic，QF_LIA)、实数集上的线性算数理论(quantifier free_linear real arithmetic，QF_LRA)、数组理论、未解释函数理论等[13]。

2.2.2 虚拟网映射问题求解

(|Ns|-1)]进行二分搜索，该区间的下界是虚拟网络所有链路的带宽之和，表示每条虚拟链路所映射的物理路径的长度至少为1；上界是虚拟网络所有链路的带宽之和与物理节点数减1之乘积，表示每条虚拟链路所映射的物理路径的长度至多为物理节点数减1。OPT-MathSA[15]、Z3[16]和SYMBA[17]等SMT求解器均能满足问题求解需要。

3 平均性能实验评估

基于SMT求解器的虚拟网映射问题精确求解方法属于一阶段映射精确算法。目前提出的求解虚拟网映射问题的精确算法，其本质是求解混合整数线性规划模型的不同方法，主要包括列生成算法(Column Generation Algorithm，CGA)[9]、最优分解法(optimal decomposition approach，ODA)[10]和采用优化软件的分枝定界法等[11-12]。

下面采用实验的方法评估基于SMT求解器的虚拟网映射问题精确求解方法的平均性能，具体把所提出的基于SMT求解器的方法同列生成算法[9]、最优分解算法[10]和基于优化软件方法[12]进行比较，虚拟网映射问题的线性整数规划数学模型采用VNM_IP。

3.1 实验环境及性能评估指标

基于Mininet和FlowVisor[18]构建仿真环境，SMT求解器采用Z3 4.4.4，优化软件CPLEX采用CPLEX11.0，优化软件LINGO采用LINGO 11.0。本实验在配置Intel(R) Core(TM) i5- 480M@ 2.67 GHz CPU，4 GB内存的电脑上进行。对基于Z3求解虚拟网映射问题的性能分析，主要使用虚拟网请求接受率、单位时间物理网络提供商的平均收益和求得虚拟网映射问题最优解所用平均时间等三个评估指标。

3.2 实验数据的设定

物理网络和虚拟网络构建采用当前研究常用的方法[2]，即采用GT-ITM[2]工具构建物理节点CPU容量和物理链路带宽均在[480,580]内均匀分布的包含30个物理节点和40条物理链路的物理网络。虚拟网络的到达是平均每5分钟有1.3个请求的泊松过程，每个虚拟网络的生存时间符合均值为5 000分钟的指数分布；虚拟网络的虚拟节点数在[2,5]间均匀分布，虚拟网络的连通度是50%，虚拟节点CPU容量和虚拟链路带宽均在[1,6]内均匀分布。另外，求解每个虚拟网映射问题的时间限定在4分钟之内。

3.3 实验结果及分析

实验发现采用优化软件CPLEX和LINGO求解性能相差很小，故下面针对采用优化软件CPLEX的结果进行分析。

(1) 基于SMT求解器的求解法提高了请求接受率和长期收益。图1和图2表明前750个虚拟网络请求到达后所有算法都能够完成构建，但随着时间的推移和请求数的不断增加，所有算法的请求接受率和平均收益就相对稳定。基于SMT求解器的求解方法的请求接受率稳定在0.809左右，比列生成算法CGA、最优分解算法ODA和基于优化软件CPLEX的方法分别提高19.2%、15.5%和9.6%；物理网络提供商单位时间(设为5分钟)平均收益稳定在17 283左右，比列生成算法CGA、最优分解算法ODA和基于优化软件CPLEX的方法分别提高20.1%、16.6%和10.9%。因虚拟网请求接受率等同于求得虚拟网映射问题最优解比例，故基于SMT求解器的求解方法求得虚拟网映射问题最优解比例稳定在0.809左右，比其他三种算法至少提高9.6%。

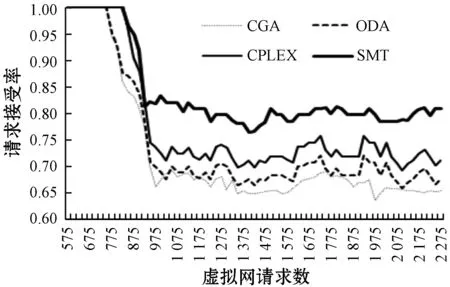
图1 虚拟网构建请求接受率

图2 物理网提供商平均收益

(2) 基于SMT求解器的求解法的最优解平均求解时间更短。从图3可观察到基于SMT求解器的求解方法，求得虚拟网映射问题最优解所用平均时间在3.43分钟左右，比列生成算法CGA、最优分解算法ODA和基于优化软件CPLEX的方法分别减少2.9%、8.1%和9.4%。从图1和图2可知，相比于列生成算法CGA、最优分解算法ODA和基于优化软件CPLEX的方法，基于SMT求解器的求解方法的物理网提供商单位时间平均收益提高幅度高于虚拟网请求接受率提高幅度至少0.9%，说明在限定时间内基于SMT求解器的求解方法能够求解出更加复杂的虚拟网映射请求，可以得出基于SMT求解器的实际求解方法的求解效率比图3所示结果更优。

图3 最优解平均求解时间

4 结 语

针对物理网不支持路径分割且物理节点不支持重复映射的虚拟网映射问题，基于可满足性模理论，构建解决虚拟网映射问题的SMT公式，并采用SMT求解器求解最优解。实验表明，与目前基于求解混合整数线性规划模型的精确算法相比，基于可满足性模理论的虚拟网映射问题求解精确方法，具有更高的有效性和实用性。后期，将对如何进一步优化虚拟网映射问题的SMT公式继续开展研究，以进一步提高求解效率。