基于随机参数Ordered Probit模型的山区公路摩托车事故严重程度研究

李小刚，田毕江，杨文臣，李 薇，岳 松

(1. 云南交投公路建设第一工程有限公司，云南 昆明 650034；2.云南省交通规划设计研究院有限公司 陆地交通气象灾害防治技术国家工程实验室，云南 昆明 650200)

0 引言

山区双车道公路是连接城市与乡镇的重要通道，由于山区双车道公路各种交通方式混行、行车环境极其复杂，且具有影响行车安全的平面交叉口、接入口、穿村镇路段等不利因素，同时缺乏中央分隔带等交通安全设施，道路安全性能较低。摩托车作为山区居民出行的主要交通工具，占山区城镇居民出行方式的比例高达30%～50%[1]。受自身性能和道路环境限制，极易引发安全事故。据统计，与其他机动化道路使用者相比，摩托车驾驶员通常因在撞车事故中缺乏保护而导致更高的死亡率和受伤率，全球大约25%的道路交通死亡事故发生在摩托车事故中[2]。根据《统计年鉴2021》，2020年我国共发生45 789起摩托车交通事故，占交通事故总数的10.14%。其中，摩托车交通事故受伤人数为53 582人，死亡人数为10 463人，占比为18.67%，山区公路上与摩托车有关的事故占比约为25%。可见，山区公路摩托车交通安全问题已成为重大的民生问题，亟需展开研究，以制订有效对策来改善农村地区摩托车交通安全水平。

国内外已有大量学者开展了关于交通事故严重程度影响因素方面的研究，但研究对象主要聚焦于数据较为丰富的高速公路和城市道路，研究方法多采用离散选择统计模型剖析交通事故严重程度的影响因素，如二分类回归法[3]、多分类回归法[4]、有序回归法[5]及随机森林法[6]等。针对摩托车事故严重程度影响因素分析，Wang等[7]以佛罗里达州摩托车单车碰撞事故为基础，分别建立了有序Logit回归、异构选择模型及广义有序选择回归模型分析水平曲线对事故伤害严重程度的影响，发现曲线半径越大事故严重程度越小。Allen等[8]采用有序Logistics模型研究摩托车事故影响因素，发现驾驶员预判错误和危险驾驶行为是导致摩托车事故的最主要原因。温惠英等[9]基于美国印第安纳州部城市道路的10 a摩托车单车碰撞事故数据，构建巢式Logit模型首次分析了单起摩托车碰撞事故严重程度影响因素，发现驾驶员性别、年龄、是否使用头盔、是否酒驾、是否超速、是否发生在农村地区等与摩托车事故严重程度显著相关。当前，国内外学者主要以城市道路的摩托车事故为研究对象，对山区公路上的摩托车事故特征及影响因素关联关系的认识较为缺乏。秦雅琴等[10]最先关注了山区公路摩托车事故，采用传统有序Logit 模型建立了摩托车事故严重度分析模型，为防治干线公路摩托车交通事故提供了一定依据。

但是，现有山区公路摩托车事故严重程度影响因素分析模型均假设解释变量对每起事故的影响具有一致性。实际上，每个个体的结果对解释变量的反应是不同的，因此不能被认为是固定的。此外，交通事故的发生是人、车、路和环境中的多个因素相互作用引发的结果。而事故调查无法全面记录与事故相关的所有影响因素，这些因素会影响参数估计和模型预测的准确性和合理性[11]。为了捕捉不同事故之间的异质性，随机参数模型逐渐被广泛应用在交通安全领域。Dinu等[12]首次将随机参数模型引入农村双车道公路事故严重程度估计研究中，并得出考虑异质性的随机参数模型相较于传统统计模型具有更佳的模型拟合效果。Chang等[13]提出了一种结合潜在类别聚类分析和随机参数Logit模型的二阶段法，对湖南省摩托车碰撞数据进行了分析，发现性别、是否搭载乘客及事故发生日等因素对摩托车事故严重程度存在异质性效应。国内学者对交通事故数据异质性的研究较少，李俊辉等[14]以2016年美国德克萨斯州3 476起货车翻车事故为研究对象，构建了货车翻车驾驶员伤害严重程度混合有序Probit 模型，发现混合有序Probit模型能捕捉到男性、饮酒等随机参数的异质性效应。朱彤等[15]采用随机参数模型分析了16个影响因素与公交车碰撞事故责任之间的定量关系，发现随机参数模型可以很好地解释数据中未观测到的异质性。

综上所述，国内外学者在摩托车交通事故严重度影响因素分析研究方面取得了一定成果，但城市道路与山区公路在交通事故特征及其影响因素等方面显著不同，且国内与国外的交通环境存在一定差异。同时，现有常用的统计分析模型存在数据同质性假设，无法刻画事故数据中的异质性，导致模型估计出现偏差。因此，有必要针对我国山区公路摩托车事故严重程度进行深入研究。为同时考虑事故严重程度的有序特性和异质性，本研究以2012—2017年发生在云南省楚雄市Y公路的504起摩托车交通事故为研究对象，采用RP-OP建立摩托车交通事故严重程度异质性分析模型，并与OP模型进行对比，以较为完善的参数估计与检验体系验证模型的有效性和准确性，得到更符合影响山区双车道公路摩托车事故严重程度的显著变量。最后结合弹性分析法确定不同显著自变量对摩托车不同等级事故严重程度的影响，以期有助于识别影响山区双车道公路摩托车交通事故严重程度的关键因素，为有关管理部门制订交通安全改善措施提供一定的理论依据。

1 数据描述

1.1 数据说明

选取云南省山区双车道公路Y为研究对象，该公路按照二级公路标准建设，全长162.03 km，设计速度为60 km/h，路基宽8.5 m，平曲线最小半径200 m，最大纵坡为6%，无中央分隔栏，路面均为改性沥青混凝土路面，年均日交通量为2 215 pcu/d。该山区公路路侧接入口密度大，且位置隐蔽、视距不良。全线村镇分布较多，路侧无隔离防护设施，行人牲畜易横穿道路，行车环境极其复杂，属于典型的山区双车道公路。

以该公路2012—2017年间发生的交通事故为研究对象，数据来源于该市交通管理部门统计汇总的格式化交通事故报表，所有事故调查均由一线有经验的交警记录上报。事故数据记录(示例)如表1所示，包含简易程序事故和一般程序事故的发生时间、事故地点、受伤人数、天气、事故认定原因、事故概况等要素。2012—2017年Y公路共发生2 234起交通事故，其中涉及摩托车的交通事故517起，占比达23.14%。经过对摩托车事故数据进行编码、赋值处理，剔除事故位置信息定位不准确、记录信息不全等数据13起，最终保留504起摩托车交通事故。

表1 交通事故数据记录信息(示例)Tab.1 Traffic accident data recording information (case)

1.2 数据处理

1.2.1 因变量构建

《道路交通管理信息采集规范》(GA/T 946.3—2011)[16]按人身伤亡或财产损失程度将交通事故严重程度划分为4个等级：死亡事故、重伤事故、轻伤事故和财产损失事故。然而，由于我国交通事故统计信息与医院交通事故受伤报告间缺乏信息共享，故无法对受伤程度进行等级划分。因此，本研究参照《道路交通管理信息采集规范》，综合已有研究[6]，将摩托车交通事故严重程度划分为轻微(Ⅰ)、严重(Ⅱ)和恶性(Ⅲ)3个等级，如表2所示，各严重程度下的事故占比分别17.06%，77.78%和5.16%。

表2 山区双车道公路摩托车交通事故严重程度划分标准Tab.2 Classification criteria of motorcycle traffic accident severity on two-lane mountainous highway

1.2.2 自变量选取

交通事故是由多重复杂因素的导致的意外事件，事故原因涉及驾驶员、车辆状况、道路条件及环境情况等方面。根据山区公路摩托车事故时空分布特征(图1)可发现摩托车事故季节分布具有规律性，冬季事故率最高，秋季事故率最低；平直路段事故率最高，但就事故严重程度而言，平曲路段恶性事故最高，占恶性事故数的46.15%。

图1 摩托车事故分布Fig.1 distributions of motorcycle accident

在此基础上，综合山区双车道公路既有事故数据中可提取的有效信息、线形设计数据和实地调研情况，从摩托车驾驶员(包括年龄、性别、操作行为、是否有责)、车辆(包括涉事车型)、道路(包括平曲线、竖曲线要素、交叉口)、环境(包括季节、工作日、光线、路表)和事故信息(包括碰撞类型)5个方面，选取16个可能影响山区双车道公路摩托车事故严重程度的潜在影响因素进行研究。各分类变量特征及描述性统计信息如表3所示。

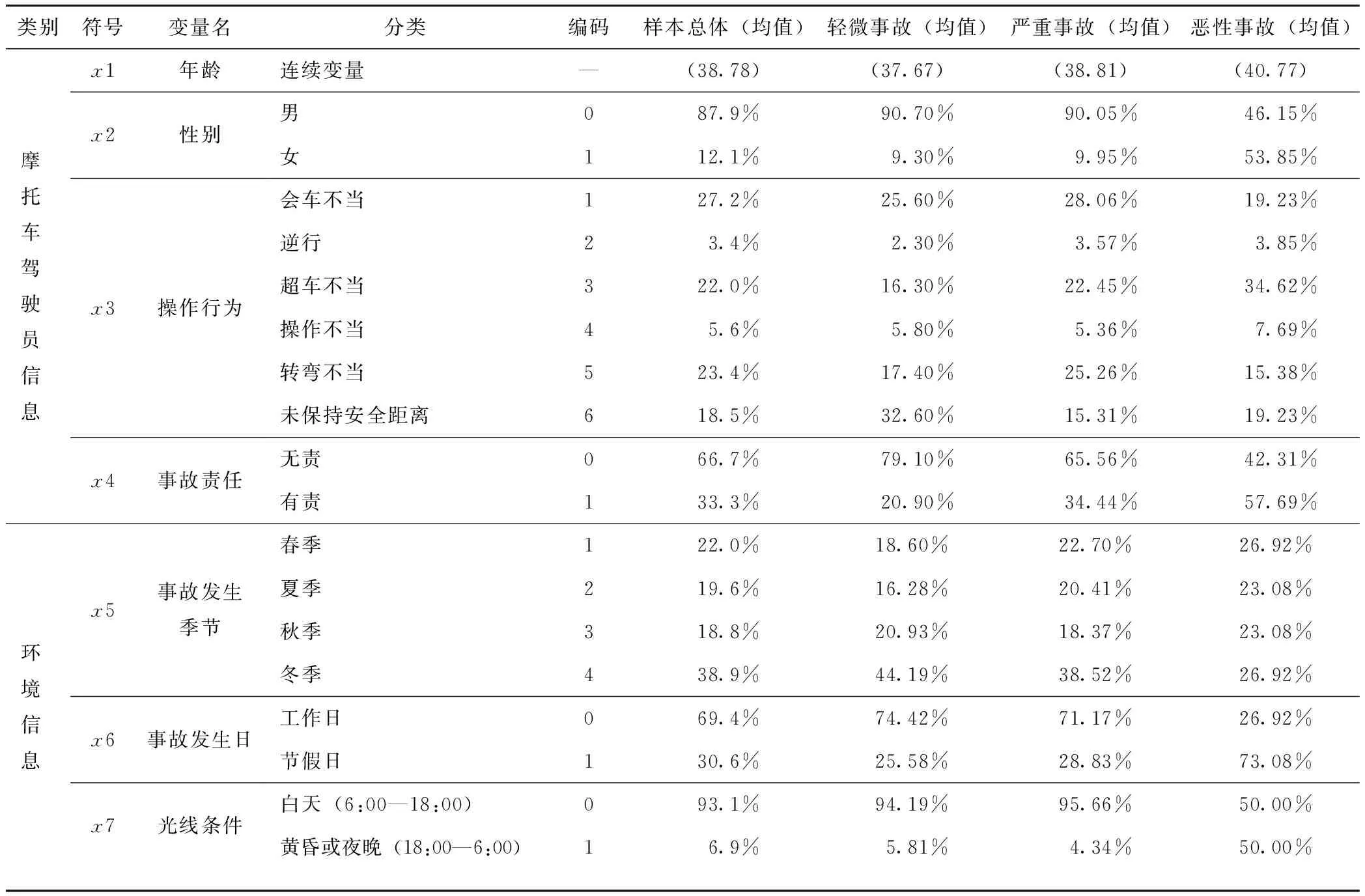
表3 自变量的定义与描述性统计Tab.3 Definition and descriptive statistics of independent variables

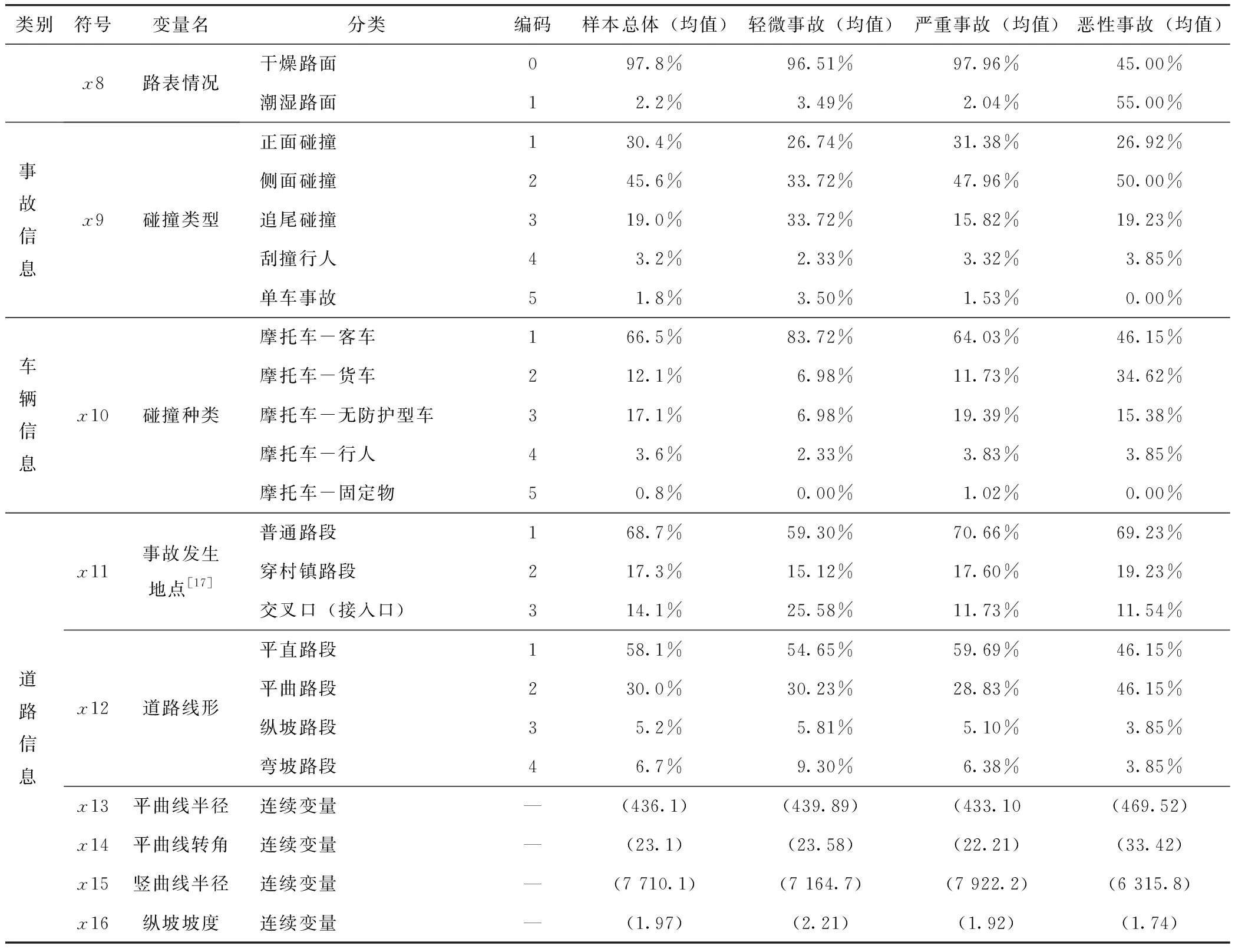
续表3

2 模型构建

2.1 随机参数有序Probit模型

(1)

式中,Xi为自变量向量；βi为系数向量；εi为误差项。

摩托车事故的严重程度yi定义为：

(2)

式中，j(j=0,1，…，J)为事故严重程度等级，本研究j有3个等级，j=0为轻微事故；j=1为严重事故；j=2为恶性事故，由阈值参数μi,j确定；μi,j为判断阈值的割点，是交通事故严重程度分级点。

不同等级的摩托车事故严重程度概率计算公式可表示为：

(3)

式中，p(y=i)为第i起事故发生事故的概率；Φ为概率密度参数向量；μi,1为第i起严重事故(j=1)的分级点。

根据现有研究[13]，在每个系数上加上1个服从正态分布的随机误差项解释个体异质性。RP-OP模型的第k个解释变量对第i起事故的随机效应计算公式为：

(4)

式中，β′ki为随机系数向量；βki为系数向量；σi为随机误差项向量，采用Halton最大似然估计得到。

2.2 模型弹性分析

由于OP模型与RP-OP模型参数估计值不能定量解释变量影响效应，本研究采用弹性系数和边际效应值量化变量对因变量的影响程度，弹性系数计算公式为：

(5)

式中，Xjk为事故严重程度等级j的第k个显著变量。但弹性系数仅适用于连续变量，对于分类变量而言，概率不能由分类值微分直接得到，可通过式(6)计算分类变量的伪弹性值[18]。

(6)

2.3 模型评价

为测试模型有效性，选取对数似然比(Log-likelihood Ratio，LR)和赤池信息准则(Akaike Information Criterion，AIC)检验山区双车道公路摩托车事故严重程度OP模型和RP-OP模型的拟合优度及其差异性[11]，计算式分别为：

LR=2[LL(βrandom)-LL(βfixed)]，

(7)

AIC=2k-2lnL，

(8)

式中，LL(βrandom)为RP-OP模型收敛时的对数似然值；LL(βfixed)为OP模型收敛时的对数似然值。似然比服从卡方分布，其自由度等于2个模型的参数差；k为模型参数数量；L为似然函数。AIC越小，卡方值越高，模型拟合优度越高[11]。

3 实证分析

3.1 参数估计

本研究使用Nlogit5.1进行模型求解，选取显著性水平为0.05，并采用逐步回归法确定显著变量，模型估计结果如表4所示。

从表4可以看出，在满足95%置信水平条件下，发现摩托车驾驶员性别、操作行为、摩托车驾驶员是否有责、是否是节假日、是否是黄昏或夜晚、路面是否潮湿、是否涉及货车及是否属于交叉口路段共8个变量与山区双车道公路摩托车事故严重程度显著相关。其中，女性驾驶员、超车、摩托车、黄昏或夜晚、路面潮湿和涉及货车7个变量与事故严重程度呈正相关关系，交叉口路段与事故严重程度呈负相关关系。

表4 OP模型和RP-OP模型的估计结果Tab.4 Estimation result by OP model and RP-OP model

由模型检验结果可知，构建山区双车道公路摩托车碰撞严重程度预测模型时，固定参数和随机参数模型间拟合优度存在较大差异，考虑异质性的RP-OP模型较OP模型拟合效果更好。具体地，RP-OP模型对数似然值从-274.954提高至-278.238，RP-OP模型的AIC值从575.9下降至576.5。同时，利用2个模型收敛时对数似然值构造似然比统计量LR值为6.567，大于6.251(自由度为3时，90%显著性水平下的卡方临界值)。表明RP-OP模型适应度高于OP模型，具有较高的拟合度。

基于OP模型参数估计结果，将OP模型中8个显著变量作为RP-OP模型的侯选变量，并假定为随机参数。运用Halton抽样法(抽样次数为200)对各显著变量进行正态分布模拟仿真。RP-OP模型结果显示，OP模型中的8个变量在RP-OP模型中均显著，且除事故发生日变量外，各变量的显著性水平均达到99.99%。女性、驾驶员超车不当及是否有货车参与3个变量参数为随机参数。

3.2 影响因素分析

基于RP-OP模型的估计结果，根据式(5)～(6)计算得到8个显著变量的边际效应值(表5)，解释各变量对山区双车道公路摩托车事故严重程度的影响方向和强度。

(1)摩托车驾驶员属性

从表4发现，摩托车驾驶员是否有责与摩托车事故严重程度显著相关。根据表5进一步得出，摩托车驾驶员有责会造成严重事故和恶性事故的概率分别增加7.68%和2.43%，对应轻微事故的概率减小110.11%。主要由于山区双车道公路弯道多、坡度大、无隔离设施，摩托车驾驶员采取逆行、超车、不按规定会车等危险驾驶行为时，往往会在道路上导致更高的事故风险及严重程度。

表5 RP-OP模型中自变量的边际效应Tab.5 Marginal effect of independent variables in RP-OP model

(2)行车环境属性

事故发生在节假日的参数估计值为0.327，说明碰撞发生在节假日时，会增加事故严重程度的发生概率。根据表5可知，节假日导致严重和恶性碰撞的概率分别增加4.22%和1.09%。原因是双车道农村公路是连接乡镇和县城的关键道路，县城或乡镇的学生或就业人员通常选择在周五和周日往返村镇和县城，导致节假日交通流量显著增加，进一步增加了双车道农村公路上摩托车事故风险。

事故发生时光线条件的参数估计值为1.568，表明黄昏或夜晚相较于其他驾驶时间，更倾向于发生严重/恶性事故。具体地，黄昏或夜晚发生轻微和严重事故的概率分别降低14.27%和10.61%，而发生恶性事故的概率将增加24.84%。因为山区双车道公路线形条件复杂，且没有照明条件，导致驾驶员视距变短，没有足够的反应时间，显著增加了严重事故的发生概率。

相比干燥的路面状况，潮湿路面更容易发生恶性事故。潮湿路面导致轻微事故的概率降低6.45%，严重事故和恶性事故的概率分别增加63.07%和1.45%。其原因是在湿滑的路面条件下，道路摩擦力大幅下降，操作不当的情况下车辆易出现失控打滑现象，导致车身侧翻、连续追尾等事故发现，增加事故严重程度。

(3)道路属性

交叉口路段参数估计值为-0.515，表明接入口路段对摩托车事故严重程度具有显著的负效应。根据前文事故位置分布统计，发现交叉口周围事故多发，死伤事故次数较为集中。但通过模型检验，交叉口路段引发严重和恶性交通事故的概率分别减小13.01%和1.28%，轻微事故的概率增大14.29%，表明交叉口并未增大山区双车道公路的摩托车事故严重程度。其原因可能是摩托车驾驶员对交叉口危险源更加敏感，往往会降低速度谨慎驾驶，因此降低事故的严重程度。

3.3 异质性结果分析

在摩托车驾驶员性别方面，随机参数异质性结果显示(表4)，女性变量对应系数服从(0.721，0.9872)的正态分布。根据正态分布累计概率计算结果可知(图2)，相比男性驾驶员，山区双车道公路上76.73%的女性摩托车驾驶员发生严重事故的概率高于男性。由边际效应结果可知(表5)，女性摩托车驾驶员发生严重事故和恶性事故的概率分别增加了5.78%和4.54%，同时轻微事故的概率降低了10.32%。这与Chang等[13]研究结论一致。摩托车驾驶员性别对事故严重程度的异质性效应是由人体生、心理多种因素共同作用导致，包括感知/反应时间、驾驶经验、对道路的注意力、视力、体重、身高等。

图2 女性参数的正态分布图Fig.2 Normal distribution of female parameter

就摩托车驾驶员操作行为而言，驾驶员超车不当变量对应系数服从(0.432，0.3442)正态分布。累积频率结果(图3)表明，山区双车道公路89.62%的摩托车驾驶员因超车不当发生严重事故的概率高于其他操作行为，而对于10.38%的驾驶员超车不当则会降低严重事故的可能性，揭示了摩托车驾驶员超车不当的异质性。表5显示，超车不当增加了发生严重和恶性事故的风险，分别增加了5.55%和1.94%，轻微事故的可能性降低了7.49%。这种异质性可能是由摩托车驾驶员不同的驾驶习惯导致。双车道上超车是较为危险的驾驶行为，驾驶人需观察本车道和对向车道的车辆，以保持安全距离。如果超车不当，易引发正向碰撞、追尾、刮擦等交通事故，但当驾驶经验丰富的驾驶员或最近发生事故的驾驶员超车时往往会产生风险补偿行为，以避免在超车时出现高风险情况。

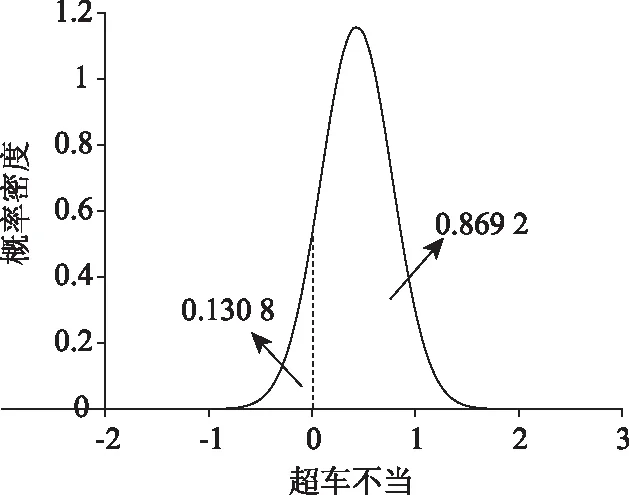
图3 超车不当参数的正态分布Fig.3 Normal distribution of improper overtaking parameter

在事故车型方面，事故涉及货车变量对应系数服从(0.723，0.5622)的正态分布。参见图4，与不涉及货车的摩托车事故相比，90.15%涉及货车时发生严重或恶性交通事故的概率大大增加，表明货车对摩托车事故严重程度的影响存在异质性效应。从边际效应结果(表5)可以看出，货车-摩托车导致严重和恶性事故的概率分别增加5.76%和4.57%，轻微事故的可能性降低10.34%。表明大多数与货车的碰撞更有可能导致摩托车事故严重程度的增加。此差异性结果可归因于货车车身高、体积大、盲区广、载重多，驾驶人行车过程中稍不注意往往易引发严重的交通事故。同时山区双车道公路弯道多、线形复杂，且摩托车稳定性较差，在发生撞车事故时摩托车驾驶员完全暴露于环境中，导致摩托车驾驶员更容易受到恶性伤害。

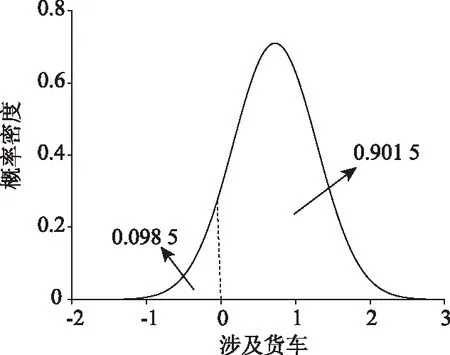
图4 涉及货车参数正态分布Fig.4 Normal distribution of involving truck parameter

4 结论

本研究以2012—2017年云南省楚雄州Y公路504起摩托车碰撞事故为研究对象，从人、车、路、环境和事故5个方面选取了16个潜在影响因素作为候选自变量，以事故严重程度为因变量，分别采用OP和RP-OP模型探究了影响山区双车道公路摩托车事故严重程度的显著因素，得到以下主要结论。

(1)OP和RP-OP模型均可识别山区双车道公路摩托车事故严重程度的关键因素，但考虑个体异质性的RP-OP模型拟合优度高于OP模型，能准确刻画未观测到的异质性和影响因素之间的交互作用。

(2)OP和RP-OP模型参数估计结果均表明，摩托车驾驶员性别、操作行为、是否有责、是否是节假日、是否是黄昏或夜晚、路面是否潮湿、是否涉及货车及是否属于交叉口路段共8个因素与山区双车道公路摩托车交通事故严重程度密切相关。RP-OP模型发现女性驾驶员、驾驶员超车不当及事故涉及货车3个参数服从正态分布，其对摩托车事故严重程度具有显著的异质性影响效应。

(3)女性摩托车驾驶员、驾驶员超车不当、摩托车驾驶员有责、节假日、黄昏或夜晚、路面潮湿、涉及货车7个因素均与山区公路摩托车事故严重度呈正相关关系，分别导致恶性事故发生概率增大4.55%，1.94%，2.43%，1.09%，24.84%，1.45%，4.57%；而交叉口路段与摩托车事故严重度呈负相关，导致恶性事故发生概率降低1.28%。

(4)与现有的事故严重程度影响因素分析模型相比，本研究建立的模型考虑了影响因素异质性，数据易获取且模型简单，便于进行山区双车道公路摩托车交通事故严重程度预测。但摩托车事故严重程度还受驾驶人个体属性(驾龄、驾驶行为)、交通流、道路环境(视距、安全防护设施)等影响，在实际运用本方法前，还需采集山区不同公路的摩托车事故数据，扩大事故样本量，进一步验证本研究成果。在后续研究中，可以进一步考虑山区双车道公路的道路条件和交通流等因素，实现更高精度的摩托车交通事故严重程度预测。