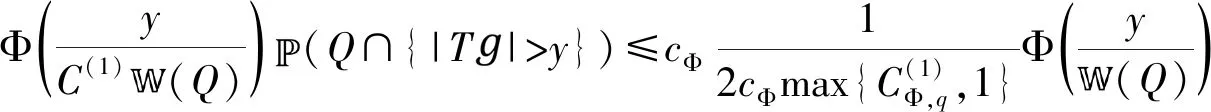弱Hardy-Orlicz-Morrey鞅空间的原子分解
陶昌玲,于 林
(三峡大学 理学院,湖北 宜昌 443002)
1 引言
在函数空间和调和分析理论中,Morrey空间的研究由来已久[1],且已取得丰富成果[2-3]。众所周知,经典的鞅Hardy空间理论是建立在Lebesgue空间Lp的基础之上[4-5]。近年来,Morrey空间理论被拓展到鞅论研究中并引起广泛关注。例如,Ho[6],陶昌玲和于林[7],分别对Hardy-Morrey鞅空间建立了不同形式的原子分解定理;Nakai-Sadasue[8]引入Morrey-Campanato鞅空间研究分数次积分算子的有界性;Jiao[9]更是将Hardy-Morrey鞅空间的研究拓展到变指数空间Lp(·)的框架之上。
最近,Yu[10]引入弱Hardy-Morrey鞅空间的概念,对此类空间建立原子分解定理,并以此为工具获得了一系列新的鞅不等式。本文旨在将这一研究进一步推广到弱Hardy-Orlicz-Morrey鞅空间。对弱Hardy-Orlicz-Morrey鞅空间证明一个所谓“混合型”原子分解定理。确切地说证明弱Hardy-Orlicz-Morrey鞅空间中的每一个鞅都可以分解为一序列弱原子的和,而每一个弱原子又可以进一步分解为一序列弱简单原子的和。正因为如此,称这里得到的原子分解为“混合型”。
这种原子分解的优点之一是,可以仅在弱简单原子满足一定条件下就能得到一些有趣的鞅不等式。例如,利用所得到的原子分解定理证明弱Hardy-Orlicz-Morrey鞅空间上次线性算子的有界性,并由此将一些经典的鞅不等式从空间推广到弱Orlicz-Morrey空间。
2 概念及引理
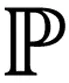

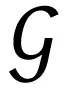




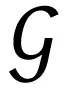
注1设Φ(t)∈Q(α0,α1),易证
Φ(st)≤max(sα0,sα1)Φ(t)。其中s,t∈(0,+∞)。
Φ(st)≤cΦmax(sα0,sα1)Φ(t)。
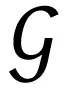
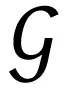
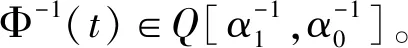
注3[6]特别地,当Φ(t)=tp(0 此外,下列等价范数成立 (1) 其中,下确界inf取遍f的所有上述原子分解。 Φ(st)≤max(sα0,sα1)Φ(t),s,t∈(0,+∞)。 (2) 由此可证(ⅱ)和(1)中的一个不等式。 (3) (4) (5) 不失一般性,不妨设A=2mA(mA≥0),且有2j≤2mA+j≤A·y=2mA·y<2mA+j+1。因此,有 因Φ∈Q[α0,α1]且0<α0≤α1<∞,则Φ(t)t-α1非增,Φ(t)t-α0非减。因此,一方面,有 另一方面,有 此外,f∈wHMΦ,φ, 由上式及(2),可以得到(1)。定理证毕。 (6) (7) 对所有0 (8) (9) (10) ‖M(f)‖wMΦ,φ≤CΦ‖s(f)‖wMΦ,φ,‖S(f)‖wMΦ,φ≤CΦ‖s(f)‖wMΦ,φ, {|M(aB)|>0}⊂{aB≠0}⊂B,{|S(aB)|>0}⊂{aB≠0}⊂B, 此外,将定理2分别应用于q=2时的M(·)和S(·),得到 ‖M(f)‖wMΦ,φ≤CΦ‖s(f)‖wMΦ,φ,‖S(f)‖wMΦ,φ≤CΦ‖s(f)‖wMΦ,φ。
3 原子分解







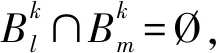
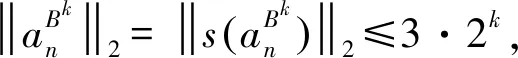
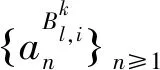
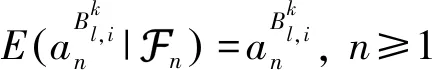

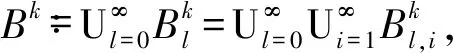



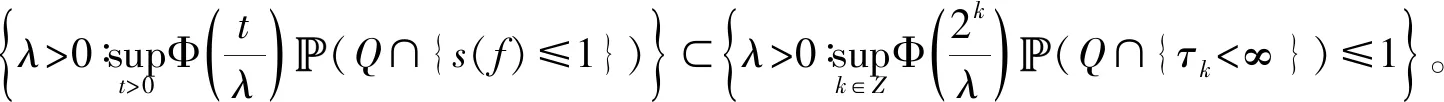
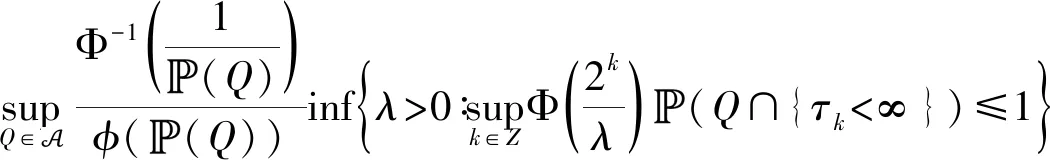


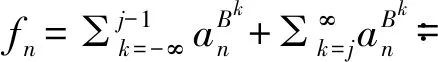

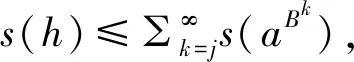
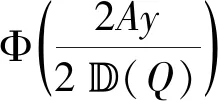
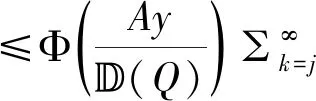
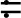
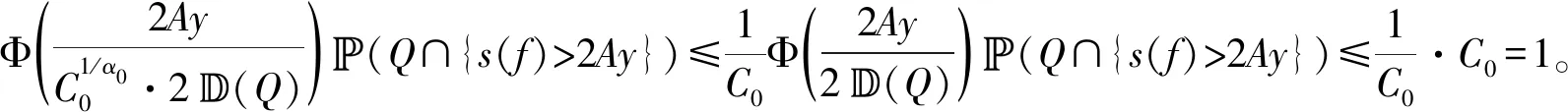

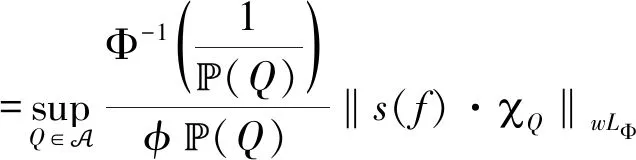
4 应用:鞅不等式