升力式航天器太阳同步冻结回归轨道保持策略

金宇帆 王 壮 闫晓东

西北工业大学航天学院，西安 710072

0 引言

面对时敏目标的观测需求，超低轨道飞行器具备快速发射入轨、高机动特性、更高分辨率的优势[1]。太阳同步冻结回归轨道，可以实现针对特定区域的对地观测任务时，飞行器经过同一星下点光照特性和轨道高度相同，且经过一个回归周期后星下点轨迹重复，能显著提高观测效果。根据上述优势，需要设计一种近地点位于超低轨道高度甚至临近空间的太阳同步冻结回归轨道。

对于太阳同步冻结回归轨道的设计与轨道保持策略的研究较少。文献[2]中提出了基于切向单脉冲的最低燃耗轨道面内保持策略，策略有效使卫星星座跟踪并捕获太阳同步冻结轨道。文献[3]中针对人工太阳同步轨道设计方法进行了研究，提出了利用施加连续推力调整升交点赤经实现太阳同步轨道的方法，能够满足太阳同步轨道的要求。文献[4]中通过分析太阳同步回归轨道的轨道根数和星下点经度/纬度的关系，推导了一组轨道根数的修正公式，结合迭代修正，得到一组严格回归的轨道根数。该轨道能够重访空间目标点，具有较高的回归精度。

运行于超低轨道的飞行器，受地球非球形引力和大气阻力摄动影响，其轨道高度会迅速衰减，为了延长飞行器在轨飞行寿命，需要研究有效的轨道保持方法。文献[5]针对低轨星座在轨运行的高精度构型保持问题,提出了一种基于极限环的高精度相位保持方法，设定参考轨道，经数值仿真验证，相位保持方法能够在卫星定轨数据精度不高、数据采样间隔较大的情况下,实现低轨星座系统的高精度相位保持。文献[6]采用以轨道根数为基础的控制方法，针对超低轨道飞行器使用离子推进器保持轨道进行仿真，验证了离子推进器对超低轨道飞行器高精度轨道保持的有效性。可见现有研究主要聚焦于应用化学推力或电推力实施轨道保持控制，一般将气动力作为阻力摄动，没有考虑气动升力对于轨道保持的作用。事实上，对于具有一定升阻比的升力式航天器而言，气动升力可在近地点位于临近空间的太阳同步冻结回归轨道保持过程中发挥重要作用，这也将是本文研究的方向。

气动力辅助变轨技术(AOT)是由London在1962年提出的概念[7]。姬聪云针对微小卫星气动力辅助变轨过程，研究分析了在变轨过程中不同的近地点高度对优化效果的影响[8]，结果表明，气动力变轨节省燃料能力随近地点高度的降低而变强，但飞行器所受的过载、驻点热流和动压也越大。左光研究了类X-37B飞行器的气动力辅助异面变轨性能，计算了变轨所需的燃料消耗量和轨道倾角改变量，并与采用冲量变轨方式的燃料消耗量进行了比较[9]，结果表明气动力辅助变轨节省燃料的能力会随着轨道倾角改变量增大而变强。可见目前针对气动力辅助变轨技术的研究集中在以燃料最省为目的的轨迹优化问题，未针对利用气动力辅助变轨技术实现例如太阳同步轨道或冻结轨道等特殊轨道的方法研究，而本文将针对这些问题进行研究分析。

轨道优化理论方面的研究兴起于20世纪三、四十年代，主要应用于航天器设计优化领域。迟进梓等针对连续小推力航天器轨道转移制导问题，将卫星变轨过程转化为两点边值问题，并引入混合遗传算法，结果表明该方法对小推力航天器变轨过程具有良好的优化效果[10]。张亚锋等研究了Gauss伪谱法在有限推力轨道转移优化问题中的应用，选取能量最优为性能指标，计算了同面和异面轨道转移过程，验证了Gauss伪谱法对于轨道转移优化问题的适用性[11]。本文也将借助Gauss伪谱法求解多段连续轨迹优化问题。

1 轨道保持问题模型

1.1 轨道保持动力学模型

为了分析飞行器稀薄大气环境飞行状态，需要建立飞行器稀薄大气动力学模型。在建模过程中进行如下假设：

(1)飞行器被视为重心不变的质点；

(2)地球为扁球体，仅考虑J2带谐项影响；

(3)大气随地球一起旋转，相对地球保持静止；

(4)在机动过程中侧滑角不存在，仅依靠攻角与 倾侧角改变气动升力方向。

经推导整理建立如下飞行器位置坐标系下动力学微分方程组：

(1)

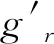
(2)

式中：α表示飞行器攻角，D和L分别表示飞行器所受气动阻力和升力，计算公式如下：

(3)

式中：ρ表示大气密度，CD和CL分别表示飞行器阻力系数和升力系数，Vr表示飞行器相对大气速度，计算公式如下：

(4)

式(1)中gωe、g′r只考虑J2项时计算公式如下：

(5)

式中：J2=1.08263×10-3，μ为地球引力常数，Re为地球半径。

在真空环境中飞行时，飞行器不受气动力影响，依靠发动机推力调整轨道参数，将控制量设定为发动机推力大小和方向，对式(1)中部分方程进行调整：

(6)

式中：ux为本体系X轴控制分量，uy为本体系Y轴控制分量，uz为本体系Z轴控制分量，up为控制量平方和。

1.2 轨道要素与状态量转换关系

在研究过程中，需要在轨道要素数据与位置坐标系下状态数据间进行变换，由位置坐标系下运动状态计算轨道要素变换关系如下：

(7)

式中：a表示半长轴，r表示位置矢量，e表示偏心率矢量，Ω表示升交点赤经，i表示轨道倾角，ω表示近地点幅角，f表示真近点角，轨道根数示意图如图1所示。

图1 经典轨道根数示意图

2 太阳同步冻结回归轨道参数设计

飞行器位于太阳同步冻结回归轨道时，在间隔回归周期时间飞行至相同地区上空时太阳对地光照情况及飞行器对地观测高度与上一回归周期一致，在应对特定区域观察任务时，设定合理的轨道参数，将轨道的近地点置于大气层内，降低观测高度，可以极大地提高飞行器对地侦察的观测效果。

设计近地点经过大气层的太阳同步冻结回归轨道，需要综合考虑地球自转、地球非球形引力摄动及大气摄动的影响，其中大气摄动作为实现太阳同步冻结回归轨道的控制量之一，在初始轨道参数设计中不予考虑，暂时忽略。

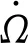
(8)

式中：TΩ为轨道周期，计算公式为：

(9)

回归轨道满足：

NΔθ=D×2π

(10)

式中：N为轨道回归周期运行圈数，D为回归周期。

对于地面时敏目标观测任务，应尽可能缩短回归周期，结合超低轨道飞行环境，设定飞行器回归周期为1d，飞行器的轨道周期为1.5h，飞行器飞行16圈后完成回归，由轨道周期计算公式(9)可以得到飞行器的轨道半长轴为6652.645km，设定轨道近地点高度为70km，则轨道远地点高度为479km。

考虑太阳同步轨道设计要求。平太阳沿着赤道作周年视运动，经365.24422个平太阳日再次经过春分点，则平太阳在赤道上移动角速度为360/365.2422=0.9856(°)/d，则每个轨道周期移动角度为0.9856°/16=0.0616°。

在只考虑地球扁率J2项影响时，升交点赤经变化率[12]为：

(11)

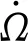
由回归轨道设定的轨道参数可以推导得到轨道倾角为96.5732°。

考虑冻结轨道设计要求。只考虑地球扁率J2项影响时，近地点辐角变化率为：

(12)

令近地点辐角变化率为0，可以推导得到轨道倾角为63.43°或116.57°。

综合太阳同步轨道和冻结轨道受地球扁率J2项影响时的轨道倾角要求，为了节省轨道调整所需燃料，取两者轨道倾角要求的中间值108°作为轨道倾角初值。

设某一区域为观测区域，考虑近地点辐角受地球非球形引力摄动影响，存在沿逆行轨道运行方向后退的现象，设定轨道初始近地点辐角为50°，升交点赤经为280°，从远地点开始飞行，则飞行器轨道初始参数设定如表1所示。

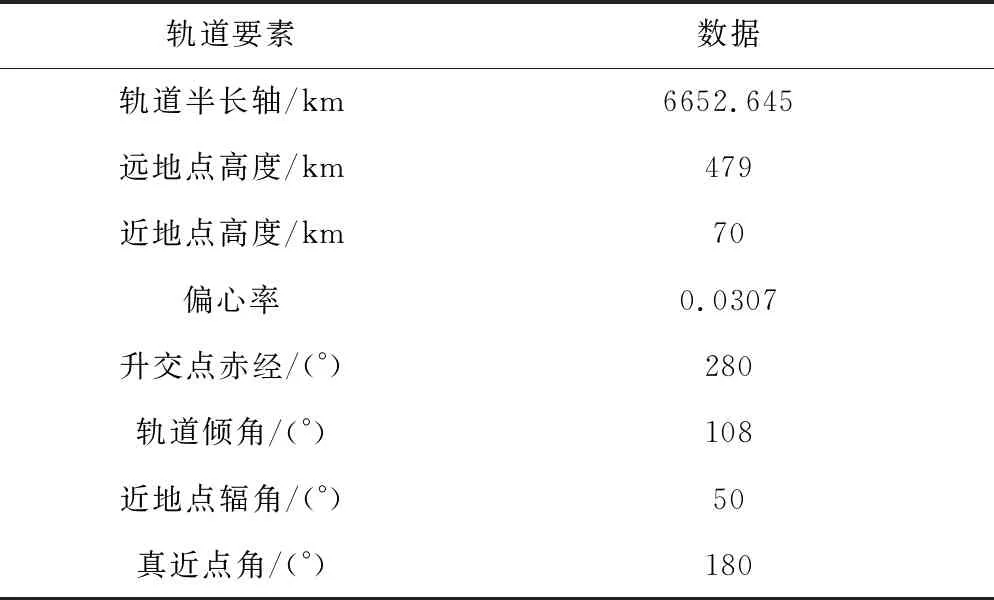
表1 轨道参数初值设定

3 太阳同步冻结回归轨道保持策略和优化模型

3.1 太阳同步冻结回归轨道保持策略

按照所设计的轨道参数，太阳同步冻结回归轨道主要受地球非球形引力摄动和大气摄动影响，轨道保持策略主要围绕2方面设计：1)克服两摄动项带来的轨道面进动过量、轨道能量衰减及近地点辐角后退等负面影响；2)利用两摄动项作用，控制轨道面进动量满足太阳同步轨道升交点赤经进动量要求。据此设计单个太阳同步冻结回归轨道周期三段式轨道保持策略：

(1)第一段为开普勒段，飞行器起始位于轨道的远地点，按照设定的轨道参数自由飞行，期间不施加任何控制量，飞行高度到达大气层边缘高度时第一段结束；

(2)第二段为大气层内飞行段，飞行器进入大气层，调整飞行器攻角和倾侧角控制飞行器气动升力，微量调整飞行器升交点赤经进动量，跃出大气层后第二段结束；

(3)第三段为动力调整段，飞行器跃出大气层后飞向轨道远地点过程，调整飞行器推力方向和大小，补充轨道能量同时调整飞行器近地点辐角，控制升交点赤经和轨道倾角，最终回到远地点时除升交点赤经外其他轨道参数回归初值，升交点赤经变化量满足单个轨道周期太阳同步回归轨道要求，完成整体轨道保持过程。

太阳同步冻结回归轨道保持过程示意图如图2所示。

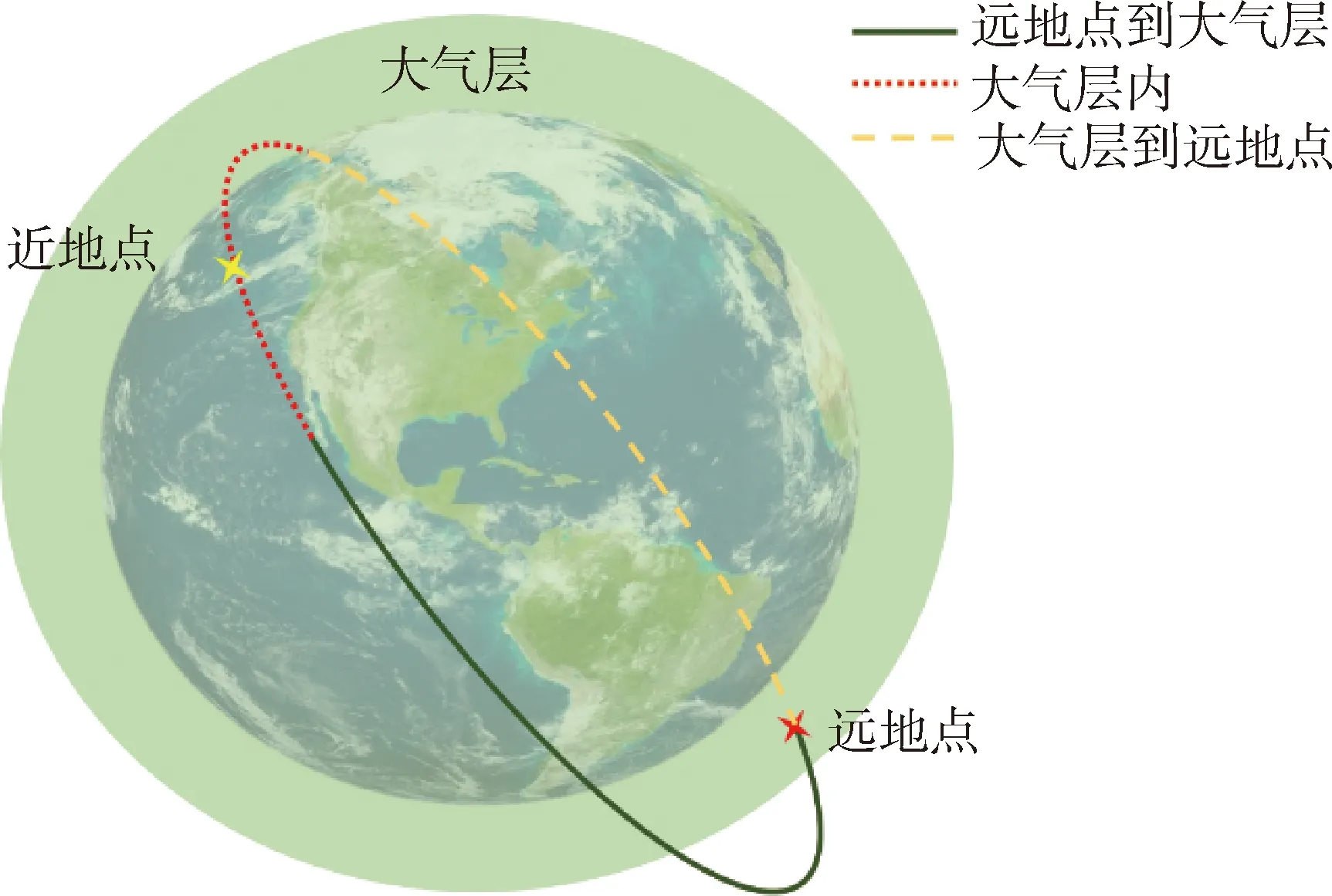
图2 太阳同步冻结回归轨道保持过程

3.2 太阳同步冻结回归轨道保持优化模型

对于太阳同步冻结回归轨道保持策略，最主要的任务就是保证飞行器在轨时间尽可能长，由此将轨道保持过程第二段和第三段归结为以燃料最省为性能指标的轨迹优化问题，设置优化模型如下：

性能指标：

J=-mtf

(13)

(1)大气层内飞行段：

优化变量约束：

(14)

状态约束：

(15)

路径约束：

(16)

(2)动力调整段：

优化变量约束：

(17)

状态约束：

(18)

路径约束：

upmin≤up≤upmax

(19)

优化问题的终端约束：

(20)

两阶段状态量满足内点约束：

(21)

式中：X(tfi)为各阶段状态量。

4 仿真验证

4.1 飞行器模型与大气模型

传统卫星由于大多服务于较高轨道高度，在设计过程中很少考虑到自身的气动特性，超低轨道气动力辅助对于传统卫星模型效果不佳，为了有效验证气动力辅助对超低轨道飞行器的作用，需要采用升力式飞行器模型进行仿真分析。

本文中采用CAV-H飞行器作为仿真验证对象，其模型参数如表2所示。

表2 CAV-H模型参数

气动加热模型为：

(22)

动压模型为：

(23)

法向过载模型为：

(24)

位于超低轨道的飞行器飞行速度大多超过Ma23，所以只取用CAV-H飞行器Ma23气动参数作为参考，为了提高优化效率，对气动参数进行拟合估计，得到如下气动参数计算公式：

(25)

其中,攻角单位为(°)，拟合后气动参数数据如表3所示。

表3 气动参数

在10°攻角情况下达到最大升阻比，在30°达到最大升力系数。

大气模型采用美国标准大气(US1976)，在本文中规定120km高度为大气边界高度。80km～120km高度大气密度如图3所示。

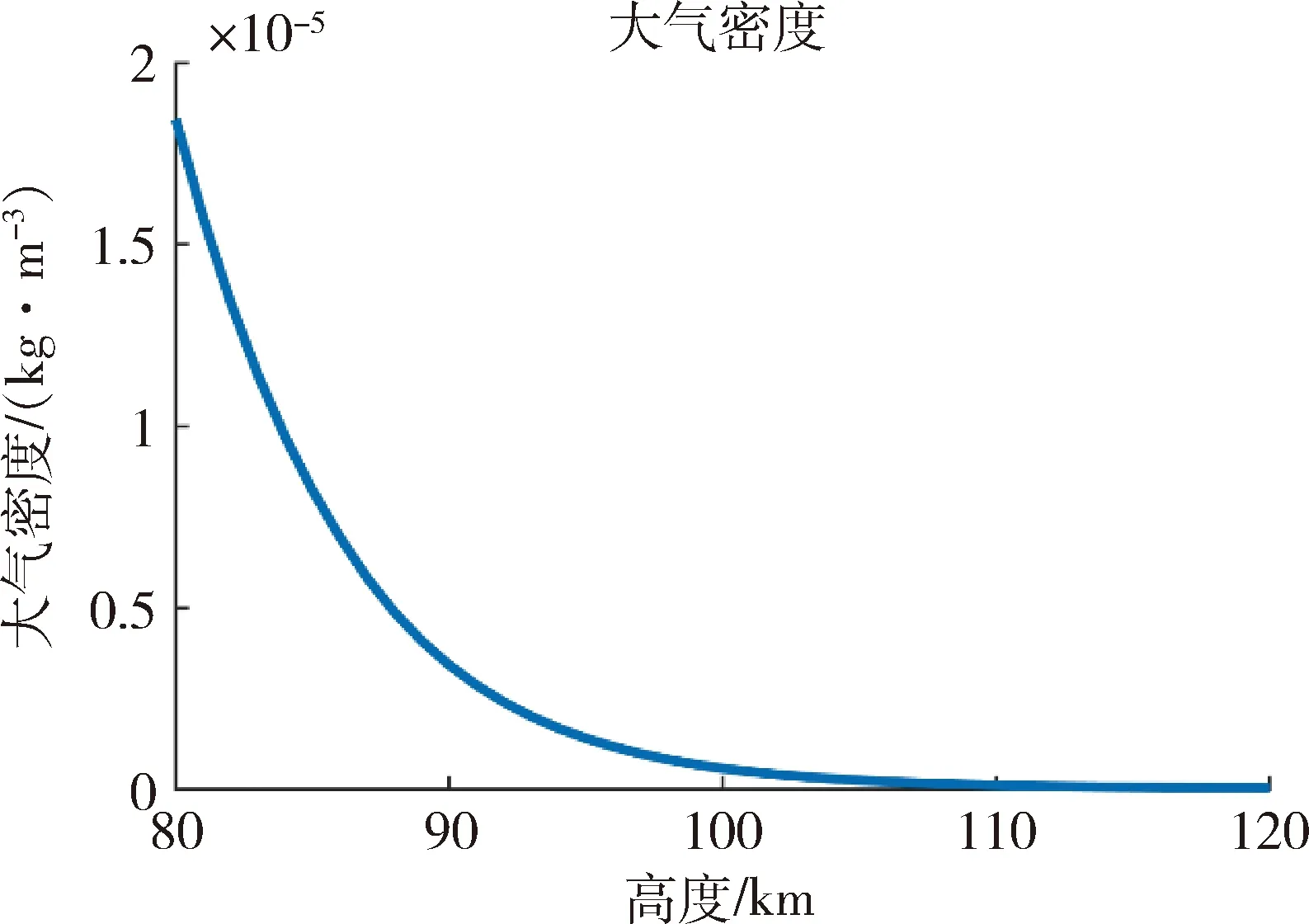
图3 大气密度

由图3可以看到，大气密度随高度降低呈指数增长，80km轨道高度大气密度高出120km轨道高度3个数量级。

4.2 策略有效性验证

为了验证策略的有效性，对表1设置的初始轨道参数，应用式(7)转换为位置坐标系下初始状态量，代入式(1)动力学模型，忽略其中动力项，进行开普勒飞行段积分计算，在到达大气层边缘时停止，得到表4所示再入大气层初始状态量。

表4 再入大气层初始状态量

设置大气层内飞行段优化变量约束及路径约束如表5所示。设置动力调整段优化变量约束及路径约束如表6所示，设置优化问题状态约束如表7所示，设置优化问题终端约束如表8所示。

表5 大气层内飞行段优化变量约束及路径约束

表6 动力调整段优化变量约束及路径约束

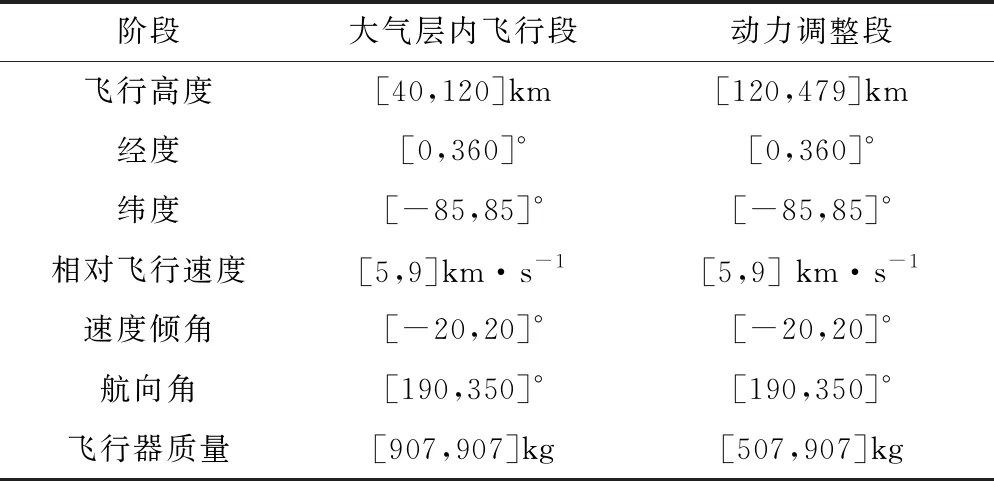
表7 状态约束

表8 终端约束

其中:升交点赤经通过式(26)计算而得：

ΔΩ=Ω0-ωeTΩ+0.9856°/16

(26)

采用高斯伪谱法和序列二次规划算法对太阳同步冻结回归轨道保持过程进行仿真分析，同时与相同初始轨道参数下不考虑大气摄动、只考虑地球自转及地球非球形引力摄动，不施加任何控制量时轨道参数变化情况进行对比，得到如表9和表10所示数据。

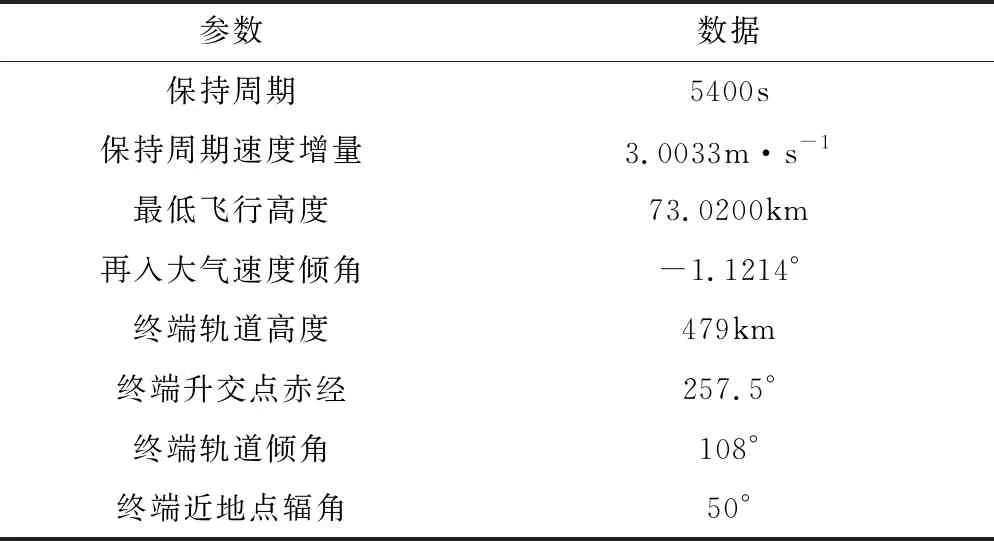
表9 轨道保持过程参数

表10 不考虑大气摄动椭圆轨道参数

由表10可以看到，在无控不考虑大气摄动情况下，在一个轨道周期内，轨道的升交点赤经进动量小于太阳同步轨道要求，近地点辐角沿飞行器飞行方向存在小幅后退，这是由于地球非球形引力摄动在当前轨道倾角大小下无法同时满足太阳同步轨道和冻结轨道的要求，为实现太阳同步冻结回归轨道必须对飞行器施加轨道控制。

由表9中数据可知，飞行器采用太阳同步冻结回归轨道保持策略时，由于气动力作用，飞行器轨道近地点高度由设计的70km提高到了73km，同时在单个轨道保持周期内，升交点赤经、近地点辐角满足太阳同步冻结轨道的要求。轨道保持过程如图4所示，为方便观察升交点赤经受大气摄动及地球非球形引力摄动影响的变化情况，在绘制升交点赤经变化过程时消除地球自转带来的升交点赤经变化。

由图4中轨道保持过程可以看到，飞行器进入大气层后，通过控制攻角与倾侧角调整所受气动力，小幅增大升交点赤经进动量以接近太阳同步轨道要求。在大气层内近地点辐角受气动阻力影响大幅后退，在动力调整段控制发动机开关以及推力方向，最终使飞行器满足太阳同步冻结回归轨道要求。

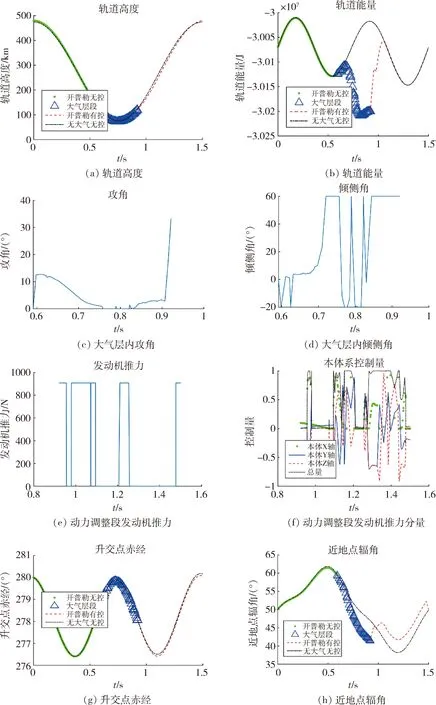
图4 单次周期轨道保持过程

4.3 24小时轨道保持过程仿真分析

为更直观观察太阳同步冻结回归轨道保持策略的有效性，采用单次周期轨道保持策略，同时连接16次轨道保持过程，对飞行器24小时太阳同步冻结回归轨道保持过程进行仿真分析，得到如表11所示结果。

表11 24小时轨道保持过程参数

由表11数据可知，飞行器按照所设计的轨道保持策略，可实现14.7d的太阳同步冻结回归轨道保持任务。经过24h飞行后升交点赤经增加0.9856°，近地点辐角和轨道倾角和初始值相同，满足太阳同步冻结回归轨道的要求。轨道保持过程如图5所示。

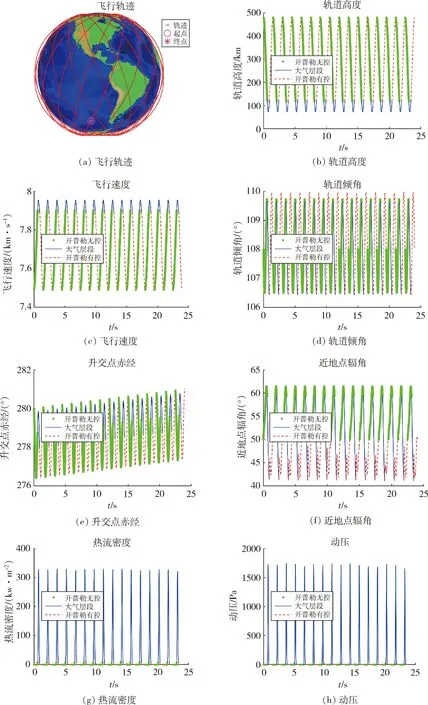
图5 24小时轨道保持过程

由图5(a)可以看到，飞行器经过24h飞行，星下点轨迹回归到起始飞行点，满足回归轨道要求；由图5(e)可以观察到，升交点赤经呈缓慢增大状态，单个轨道保持周期增大0.0616°，在24h轨道保持过程后最终增大0.9856°，满足太阳同步轨道要求；由图5(d)和(f)可以观察到，近地点辐角和轨道倾角在单个轨道保持周期相同的时间大小相同，满足冻结轨道要求；同时由图5(g)和(h)可以看到，飞行器在大气层内承受的峰值动压和热流都比较小，飞行包线具有可行性。

5 结论

本文以升力式飞行器为对象，以航天器对地侦察任务为需求，结合超低轨道飞行器对地观测的优势与升力式飞行器较强的机动能力，设计了一种近地点位于临近空间的太阳同步冻结回归轨道，并设计了气动力结合发动机推力的轨道保持策略与优化方法。针对太阳同步冻结回归轨道保持过程进行了飞行仿真和速度增量需求分析，结果表明：

1)通过设计合理的轨道倾角，利用地球非球形引力摄动，同时控制飞行器所受气动力，飞行器可以满足太阳同步轨道要求。若加以控制利用，两者对于飞行器在轨运行具有积极影响；

2)结合气动力与发动机推力的轨道保持策略，可以实现升力式飞行器14.7d的太阳同步冻结回归轨道保持任务。