高考中志在必得的复数题

焦娅琼

(山东省淄博市张店区第一中学)

复数专题内容是高考热点,主要以选择题或填空题的形式出现,考查复数的概念、复数的四则运算、复数的模及复数的几何意义等,难度较小.本文以2022年高考真题为例,分析总结复数的考查方向.

1 真题再现

真题1(2022年新高考Ⅰ卷2)若i(1－z)＝1,则＝( ).

A.－2 B.－1 C.1 D.2

真题2(2022年新高考Ⅱ卷2)(2＋2i)(1－2i)＝( ).

A.－2＋4i B.－2－4i

C.6＋2i D.6－2i

真题3(2022年全国甲卷理1)若z＝－1＋＝( ).

真题4(2022年全国甲卷文3)若,则＝( ).

由于z＝1＋i,故2－2i,则,故选D.

真题5(2022年全国乙卷理2)已知z＝1－2i,且,其中a,b为实数,则( ).

A.a＝1,b＝－2 B.a＝－1,b＝2

C.a＝1,b＝2 D.a＝－1,－b＝2因为z＝1－2i,且z＋＋b＝0,所以(1－2i)＋a(1＋2i)＋b＝(1＋a＋b)＋(－2＋2a)i＝0,所以得a＝1,b＝－2,故选A.

真题6(2022年全国乙卷文2)设(1＋2i)a＋b＝2i,其中a,b为实数,则( ).

A.a＝1,b＝－1 B.a＝1,b＝1

C.a＝－1,b＝1 D.a＝－1,b＝－1

2 回归课本

回归到课本中,复数专题主要有以下几个考点.

考点1考查复数的概念.如表1所示,处理复数概念问题时,一般采用定义法解决.

表1

基本方法将复数问题实数化,这是解决复数问题最基本的思想方法.

考点2考查复数的运算.如表2所示,在处理复数四则运算问题时,一般按照运算法则进行,应加强数据处理能力的训练.

表2

基本方法先把复数z用复数的代数形式表示出来,再用待定系数法求解,这是解决复数运算问题的基本方法.

考点3考查复数的几何意义如表3所示.

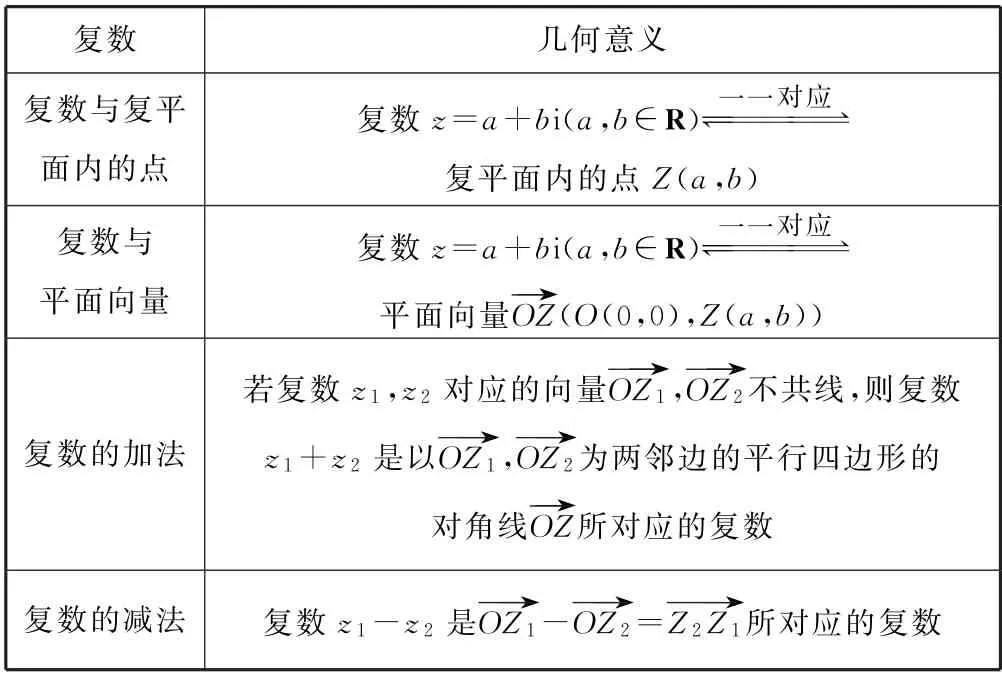
表3

3 创新模拟

4 拓展延伸

图1

复数乘、除运算的三角表示:已知复数z1＝r1(cosθ1＋isinθ1),z2＝r2(cosθ2＋isinθ2),则

5 综合评价

从近几年高考情况来看,考查的重点仍是复数的四则运算,也兼顾考查复数的几何意义、求模、共轭复数等基本知识,既属于简单题,也属于易错题.对于综合创新的考查形式,求解瓶颈是“转化”,在充分理解题意的基础上化“生”为“熟”,考试中力求快、准、稳.

(完)