野战机场体系布局韧性研究*
陈一村,陶西贵,冯进技,赵 健,朱 云
(军事科学院国防工程研究院,北京 100850)
0 引言
机场是战场设施体系的重要组成部分,是保障战机夺取制空权最直接的支撑设施,也是攻防对抗中极具脆弱性且易受敌袭击的设施[1-3]。机场体系按照时间维度划分,可分为永备机场和野战机场。其中,永备机场在战争初期往往就已经暴露,难以伪装,作为“活靶子”易被敌多波次打击造成保障中断。同时,永备机场在修建时位置固定,难以全方位满足战场上力量投送和物资补给等动态多样化需求。而野战机场具有修建速度快、可部署点位多、机动性强以及作战运用方式灵活多样等特征,容易隐蔽和伪装,是战时完成临时性、紧迫性军事任务的重要补充。如,俄罗斯建造多个野战机场加强对北极地区控制力,一旦发生异常情况,野战机场就由待命状态转为战时状态,快速承担该地区战机起降和弹药补充等任务。
因此,构建布局合理的野战机场体系,提高野战机场在敌打击下的作战保障效能,是战场设施体系作战保障能力研究的前沿[4-7]。在以往针对机场空间布局的研究中,大多聚焦单个机场选址优化[6,8]和作战保障效能评估[9-10]等研究上,基于体系空间布局的定量研究鲜见。而实际上,体系对抗作为未来战争的主要特征之一,重要程度高、保障能力强的单个点位,在攻防对抗时更容易成为打击重点,进而对体系造成巨大损伤[11-14]。因此,为避免形成重点依赖少数高价值、高能力目标的脆弱野战机场体系,在野战机场进行部署时,必须考虑敌攻击策略来优化整个体系的空间布局,建设韧性布局的野战机场体系提高生存能力和保障能力。
受空间布局制约,野战机场体系内机场数量与作战保障效能并不是呈线性关系。一方面,战场中适合建造野战机场的点位是有限的,且由于人力、物资和费用等多方面约束,野战机场体系内各节点的数量和容量受制约,不可能完全发挥所有节点最大能力。另一方面,野战机场在完成相应保障任务时,受体系内节点间的衔接性、网络连通性以及敌袭击策略等影响,野战机场保障能力也是呈动态随机变化的。因此,依据作战需求,快速部署形成保障可靠的野战机场体系韧性布局,是当前亟需解决的难题。
鉴于此,针对野战机场体系韧性布局问题,以野战机场体系最大化作战保障能力为目标,考虑野战机场潜在点位、最大保障范围、作战需求可达性和建设资源总量等约束,建立战时随机破坏条件下体系韧性布局模型,利用群智能算法和蒙特卡罗随机试验,快速求解可行的空间布局方案并进行优化。以某野战机场体系为例,量化分析了不同空间布局策略对体系作战保障能力的影响,以期为野战机场体系的快速构设和作战运用提供决策支撑。
1 需求可达性及分配模型
1.1 模型假设
战时构设的野战机场体系中,作战指挥员总是力图在有限的人力、装备和物资等条件下,最大化的满足作战需求,同时会尽可能提高作战需求的满足程度,结合野战机场任务特征,本文作出以下假设:
1)作战指挥员本着最大化满足作战需求原则,会在有限的人力、装备和物资等条件下最大化进行野战机场体系建设;
2)结合野战机场体系快速构设的时效性和隐蔽性等特征,敌随机攻击条件下会造成体系内部分野战机场(节点)失效;
3)各作战需求本着便捷性原则,在选择不同野战机场时,会依据机场的可达性按比例进行分配;
4)野战机场体系主要涉及同一类型野战机场及其对应的作战需求,其建设费用、作战需求的保障范围等能力参数相同;
5)考虑野战机场对战线、起降区域地面平整度和道面承载力等相关要求,体系各节点的位置应从潜在部署点位上进行选取,且节点间距离在40 km以内潜在部署点位不设置两个同向跑道机场。
1.2 作战需求可达性分析
在实际场景中,人员往往会偏向选择邻近的、到达时间较短的机场进行服务[15-17]。因此,考虑野战机场体系内节点最大保障能力、作战需求与机场距离以及其他因素影响,任意作战需求点i 对野战机场体系内任意节点k 的可达性aik可表示为:
式中,N1和N2分别表示作战需求点和野战机场潜在点位的集合;dma(xkm)表示野战机场的最大保障覆盖半径;di(kkm)和(km/h)分别表示需求点i 到达机场节点k 的距离和速度;η1为常量修正系数,表示战场环境、我军战场通行能力和敌军作战能力等其他影响因素对机场可达性的修正。式(1)表明在野战机场体系内,作战需求的可达性主要受需求点到对应野战机场所耗费的实际时间影响,且时间越短,可达性越强。
1.3 野战机场需求分配模型
随着敌我双方对抗的深入,作战需求一般沿战线呈分散、无序分布,而野战机场的最大保障范围和保障能力有限。为了尽可能满足战场区域内全部需求点的作战需求量,需要多个野战机场成体系共同作用,其首先面临的就是野战机场分配问题。因此,基于模型假设,野战机场体系作战需求分配模型可表示为:
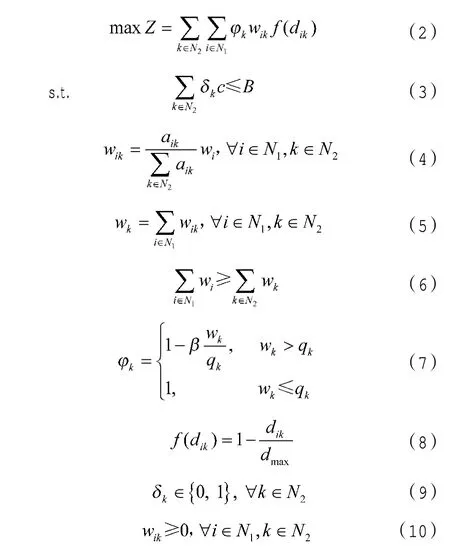
式中,Z 表示目标函数,体现野战机场体系的作战需求满足度;wi表示需求点i 的作战需求总量;wik表示节点k 承担来自于需求点i 的作战需求量;wk表示节点k 承担的作战需求总量;qk表示节点k 的最大保障能力;c 表示单个野战机场建设所需资源量;B 表示可用的野战机场体系总建设资源量;表示衰减系数;(fdik)表示在交战过程,我方前往野战机场路途中作战需求的损失量,是以dik为自变量的单调递减函数;δk为整数自变量,取值为0 或1。
式(2)表明,当wk不大于最大保障能力qk时,其作战需求满足程度随wk增大而增大,否则会进行部分衰减,这也符合现实条件,即当作战需求远高于野战机场能力时,野战机场超负荷运行,并不会完全满足所有的作战需求。同时,随着作战需求点与野战机场距离增大,f(dik)减少,表明需求点到达机场的难度会增加;式(3)表示野战机场体系总建设资源约束;式(4)~式(6)分别表示野战机场可达性与承担各需求点对应作战需求量的守恒关系;式(7)表示野战机场承担的作战需求总量wk一旦超过其最大保障能力qk,衰减系数将会利用β(0<β<1)对目标函数进行相应折减,防止野战机场过度超负荷运行;式(8)表示dik越大,f(dik)越小,其最大值为1。式(9)表示自变量δk的取值范围,当潜在点位k 部署野战机场时δk取值为1,否则为0;式(10)在整个野战机场体系中,作战需求量具有非负性。
2 随机破坏条件下野战机场体系韧性布局分析模型
在实际作战场景下,当作战需求点位及需求量确定后,我方在一定时间段内可依据潜在部署点位隐蔽快速的完成野战机场体系部署[18-19]。但是,在这一过程中,仍会面临敌快速精确打击的风险,出现部分野战机场(节点)失效的情景,进而影响野战机场体系保障能力生成。因此,要实现野战机场体系韧性布局,必须考虑随机破坏条件下野战机场体系的作战保障能力。
对此,可采用蒙特卡罗方法来对野战机场体系进行随机失效统计试验。首先,根据野战机场体系需求可达性及需求分配模型,可以得到m 组较优的野战机场体系布局Gm,其满足作战需求的程度为Zm(G)。针对任意一种体系布局,开展P 轮次模拟。在第p 次模拟中,随机选择失效节点(破坏事件e),则野战机场体系空间布局发生改变,节点k 承担来自于需求点i 的作战需求量wik将发生变化,此时满足作战需求的程度将变为。因此,随机破坏条件下野战机场体系韧性布局R 的分析流程如图1 所示,可表示为:

图1 随机破坏条件下野战机场体系韧性布局分析模型Fig.1 Analysis model of field airfield system resilience layout under random destruction condition
其中,R 表示随机破坏事件后,野战机场体系满足作战需求的韧性程度;N3表示第p 次模拟时,随机破坏事件下野战机场的集合。其他约束条件为式(3)~式(10)。
3 求解流程与算法设计
3.1 模型分析
野战机场体系韧性布局分析模型本质上是基于需求分配模型的进一步随机破坏分析,一般需要针对每一种可行的体系布局方案开展数百轮次随机分析,而需求分配模型能够产生的符合约束条件的体系布局方案数量较多,且随潜在部署点位规模扩大呈爆炸式增长,很难通过枚举方法进行比较分析。如,假定野战机场潜在部署点位数量为20 个,则其部署方案将达到220>1 000 000。
因此,将每一种野战机场体系布局作为一个可行解,必须控制进行随机破坏分析的可行解数量。但是,随机破坏条件下野战机场体系韧性布局分析模型具有非线性。其中,每一种可行体系布局方案求解是典型的0~1 整数规划问题,求解方法通常包括解析方法和启发式算法[20]。其中,解析方法通常需要将问题等价或约束松弛转化为线性规划问题进行分析,但转化难度高且计算效率低。而相比于解析方法,启发式算法不直接依赖模型的数学性质,可以快速的获得近似全局最优解。因此,本文基于粒子群智能算法来生成可行的野战机场体系的韧性布局。
3.2 算法设计

其中,α 表示惯性权重,其值越大表明粒子i 对自身速度延续的程度越高;ζ1和ζ2分别表示粒子i 朝自身和群体历史极值位置所在方向移动的学习因子;r1和r2分别表示粒子随自身和群体移动的随机性,每次速度更新时随机生成,其取值范围在0~1 之间;vmax和vmin分别表示粒子i 移动的最大速度和最小速度,主要避免粒子因速度过大跳过全局极值位置,或因速度过小陷入局部极值无法摆脱。在粒子群体不断迭代优化和趋向移动搜索的过程中,一旦群体发现最优解且后续不再发现其他更优解存在,粒子群体将利用式(13)和式(14)来调整自身的速度和位置,总体上不断趋近更优解所在的位置。
3.3 野战机场体系韧性布局方法
依据作战需求点和潜在部署点位的分布,通过粒子群智能算法,可以选取一定数量规模的较优解作为随机破坏试验条件下野战机场体系的初始布局。而在随机破坏试验条件中,敌方一般仅能掌握少量野战机场部署点位,很难在较短时间内摸清我方野战机场体系的总体部署,进而其选择目标时就会具有随机性。因此,通过选取一定数量的较优布局方案作为初始条件,利用蒙特卡罗法进行多轮次计算分析,当随机试验达到一定规模时,就可以分析和比较得到随机破坏条件下的总体部署方案,实现野战机场体系的韧性布局。
下页图2 为随机破坏条件下,基于作战需求可达性和分配模型的野战机场体系韧性布局方法流程。主要步骤如下:
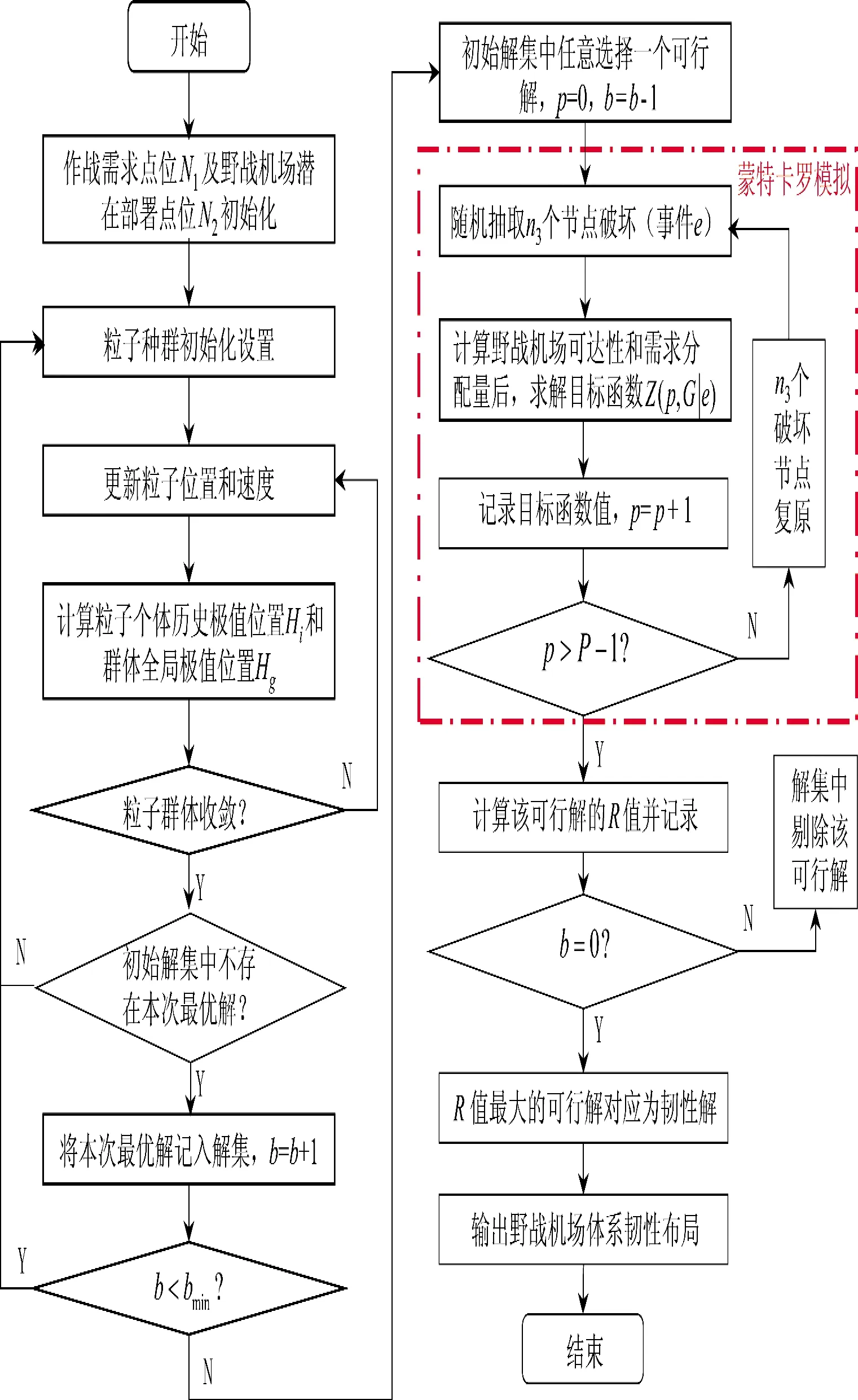
图2 随机破坏条件下野战机场体系韧性布局方法流程Fig.2 Method flow of field airfield system resilience layout under random destruction condition
1)参数的初始化设置。主要根据不同场景中作战需求点集合N1和潜在野战机场部署点集合N2,将野战机场等参数初始化,并定义f(dik)函数,同时将粒子群体数量n、解空间维度k 以及每个粒子i 的初始位置Xi和初始速度Vi等参数初始化,同时初始解集设置为空集;
2)粒子位置更新与收敛判断。依据式(13)~式(14),更新粒子位置和速度,并依据式(2)~ 式(10)计算各粒子的目标函数值Z,进而对比分析得到个体历史极值Hi和全局极值Hg。当粒子群体在一定时间段内全局极值不再发生变化或迭代次数达到最大限定时间后,则认定粒子群体收敛,进入下一步,否则,继续更新粒子位置和速度,寻找更优全局极值;
3)初始空间布局方案解集生成。判断全局极值所对应的最优解是否在初始解集中,若不存在,则记入初始解集中,否则,返回粒子种群初始化设置。此外,记入初始解集后,判断初始解集的规模b 是否小于规定数量bmin,若小于,则返回粒子种群初始化设置以重新开始寻优,否则,进入下一步,针对初始解集的任一解进行多轮次随机破坏分析;
4)蒙特卡罗模拟。选取初始解集中的可行解进行P 次随机破坏试验后从解集中剔除,直至解集为空集。任意可行解在一次随机破坏试验中,均有n3个节点随机遭到破坏,对应的野战机场失效,不再具备保障能力,进而作战需求的可达性和对应机场的需求分配发生改变,形成新的动态平衡,其目标函数值为Z(p,G|e);P 次随机试验后取平均值即为该可行解对应空间布局方案的R 值;
5)野战机场体系韧性布局方案生成。将初始解集中所有解的R 值进行比较分析,输出最大值对应的空间布局方案,该方案即为野战机场体系的韧性布局。
4 案例设置
如图3 所示为一个几何尺寸为340 km×260 km的矩形区域,每个正方形几何尺寸为20 km×20 km,17×13 个正方形覆盖了由点划线围绕的整个交战区域,共包含30 个作战需求点(N1),22 个野战机场潜在部署点位(N2)。受行动时间和作战条件限制,利用潜在点位实际部署野战机场,其满足作战需求的最大保障覆盖半径dmax为90 km。此外,为便于计算,将作战需求量在每个正方形中位置中心化,并将建设资源量和需求量进行单位化。

图3 作战需求点和野战机场潜在部署点位分布示意图Fig.3 Schematic diagram of operational demand points and potential deployment points of field airfields
因此,在案例设置中,通过网格划分,各作战需求点和潜在部署点位可通过网格中心点的坐标进行一一对应,其序号、坐标和作战需求量wi如下页表1 所示。同时,野战机场修正系数η1、最大保障能力qk和建设资源量c,以及粒子群智能算法中群体数量n 和解空间维度l 等参数的初始化设置如表2所示。其中,每个粒子i 的初始位置Xi和初始速度Vi在可行域中随机产生。

表2 案例其他相关参数设置Table 2 The other parameters setting for different types of airports
由表1 和2 可知,该区域作战需求总量为1 600,单个野战机场最大保障能力和建设资源为260 和10,当前建设总资源为80。因此,最大可建设包含8个节点的野战机场体系,最大保障能力满足作战需求总量。此外,考虑野战机场体系的节点规模和计算效率,设置初始解集规模为4,同时每个可行解均进行200 次随机破坏试验,每次试验随机选择2 个机场节点进行破坏,进而通过统计分析可得到野战机场体系的韧性布局。
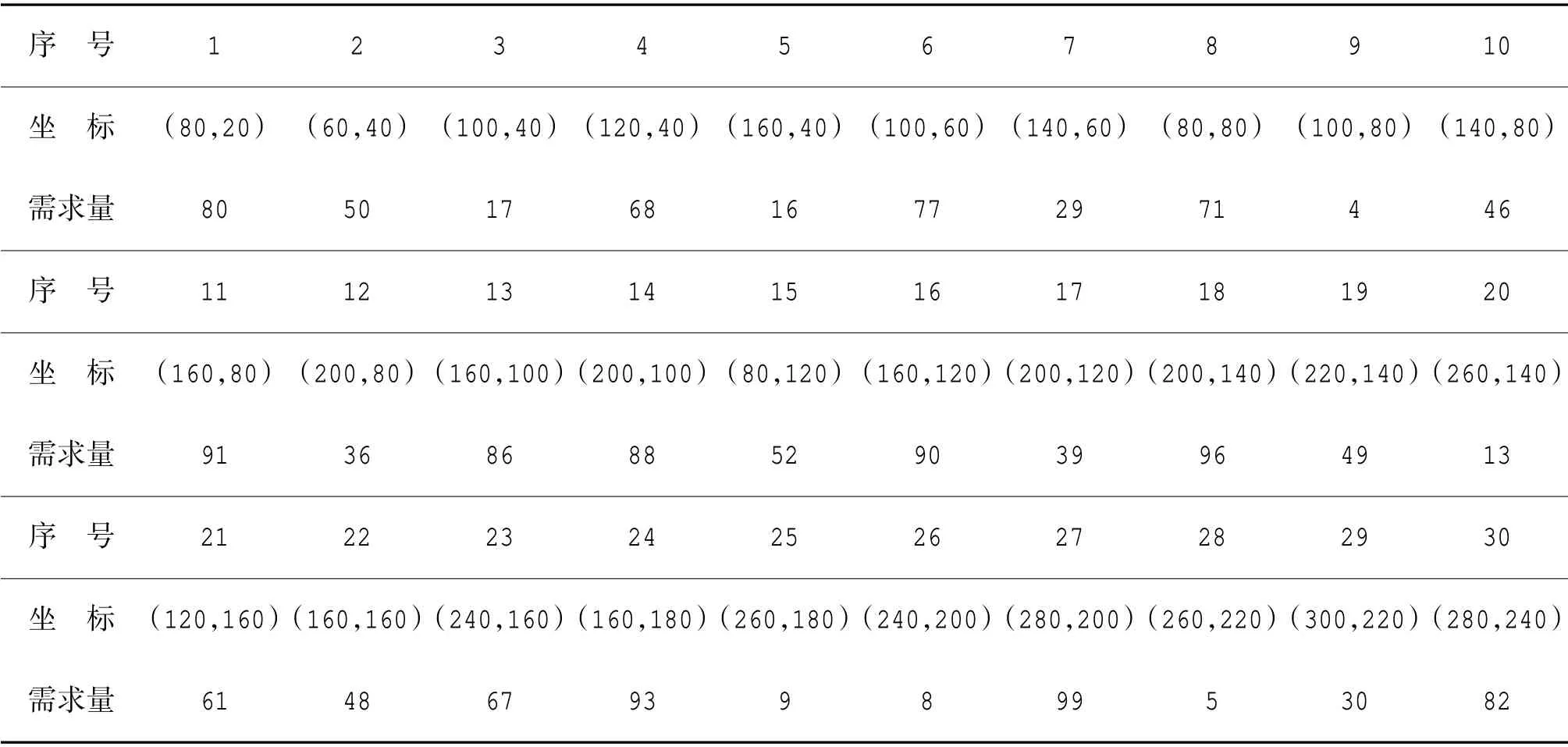
表1 作战需求点位坐标及需求量Table 1 Coordinates and demand of operational demand points
5 结果分析与讨论
5.1 野战机场体系空间分布的初始解集
针对案例设置,本文选取种群为200 的粒子群智能算法,限定每轮次迭代次数为100 作为粒子群收敛条件,最终通过4 轮次迭代,得到了包含4 个较优可行解的野战机场空间布局的初始解集,其迭代过程、对应的野战机场体系空间布局形态和节点保障范围如下页图4 所示。从图4 中目标函数的变化曲线可以看出,利用粒子群智能算法,每轮次迭代可快速收敛,并且野战机场体系在分布上能够保障所有作战需求点。由于算法的随机性,每轮次目标函数Z 的结果均不同,具有较强的波动特征,但均优于初始时刻的目标函数值。
因此,在4 轮次迭代得到的初始解集中,野战机场体系空间布局对应目标函数Z(作战需求满足度)的较优最高值为848.17,较优最低值为825.76。其中,图4(a)、(c)和(d)均部署了8 个野战机场,图4(b)部署了9 个野战机场,资源利用较多,这表明野战机场体系内节点数量越多,体系的作战需求满足度并不会越高,两者之间不存在相关关系。
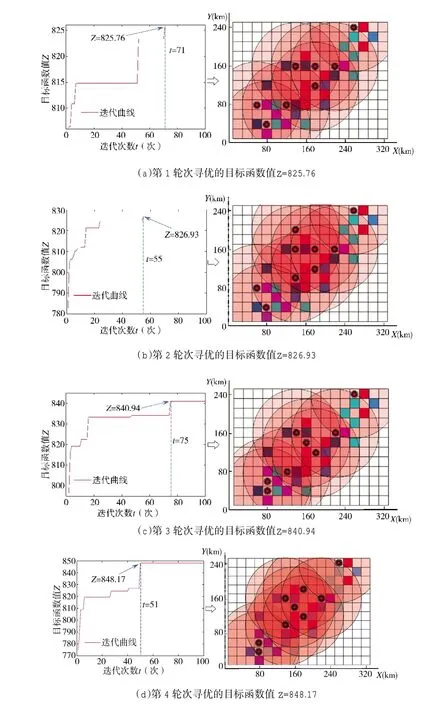
图4 初始解集求解迭代过程及其野战机场体系对应空间分布Fig.4 Iterative process of initial solution set and corresponding spatial distribution of field airfield system
5.2 野战机场体系韧性布局方案分析
针对初始解集中4 个不同的较优可行解,根据式(3)~式(12),采用蒙特卡罗方法,考虑2 个节点遭受袭击破坏失效情景进行200 次独立随机试验。其中,野战机场体系在部分节点失效前作战需求满足度Z、失效后韧性程度R、作战需求满足度最大值和最小值及其对应失效节点坐标如156 页表3 所示。
由表3 可知,基于随机破坏条件下野战机场体系韧性布局模型,能够实现野战机场体系的韧性布局,既满足作战需求的同时,兼顾随机打击的情景。在4 个初始可行解中,第3 轮次求解得到的空间布局方案在面临2 个节点失效情景中,体系韧性程度取值最高,且其失效前也具备较好的保障能力。第3轮次的空间布局方案,在包含8 个节点的野战机场体系内,位置为(220,160)和(260,240)的2 个节点破坏时,其出现最不利情景,作战需求满足度为655.34,相比于失效前,下降了22.07%。而第2 轮次中,尽管其体系内包含9 个节点,但在位置为(260,240)和(80,40)的2 个节点破坏时,出现最不利情况下,低于其他3 种空间布局方案最不利情况对应的作战需求满足度。
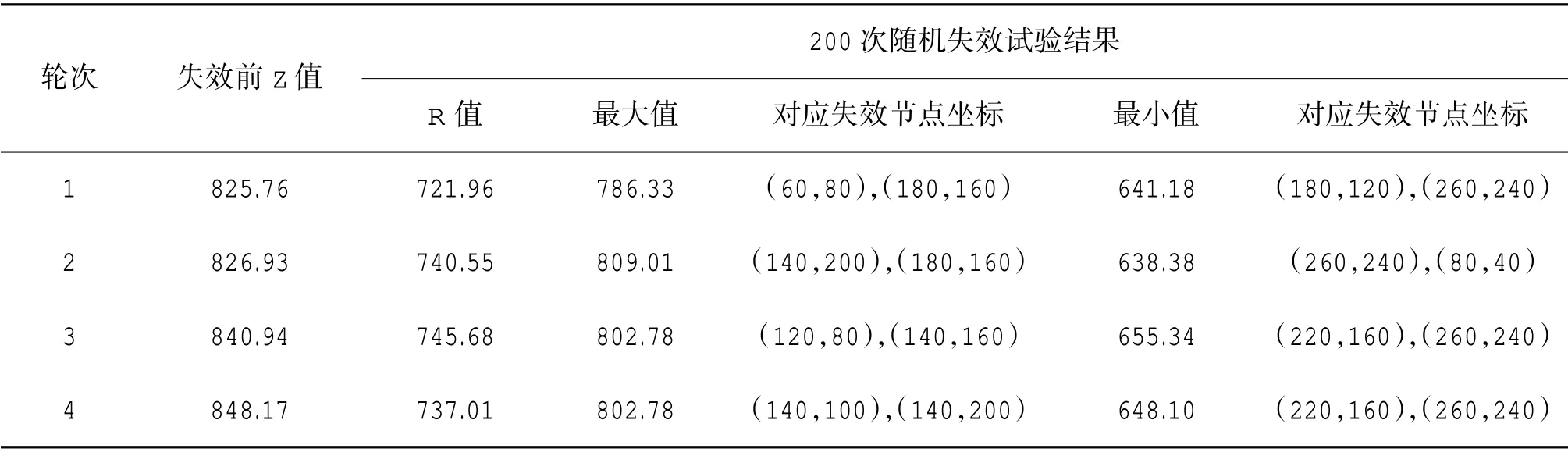
表3 初始解集200 次随机试验的计算结果Table 3 Calculation results of initial solution set of 200 randomized trials
案例研究结果表明,在不考虑敌打击失效情景下的野战机场体系的最优空间布局方案(第4 轮次),其体系面临打击后的作战需求满足度低于次优布局方案(第2、3 轮次)。一方面,战时敌打击具有随机不确定性,在信息受限条件下很难快速形成最优打击方案。另一方面,在节点失效后,第2、3 轮次的空间布局方案中失效节点的临近节点对其支撑作用更为显著。因此,为形成野战机场体系韧性布局,增强作战保障能力,必须考虑战时机场节点失效情景,以提前规划更为合理的空间布局。
6 结论
本文针对野战机场战时空间规划布局问题,以野战机场体系最大化作战保障能力为目标,考虑野战机场潜在点位、最大保障范围、需求可达性和建设资源总量等约束,建立了随机破坏条件下野战机场体系韧性布局模型,并设计相应算法,为后续开展多约束条件下永备机场和野战机场相结合的韧性布局研究提供理论基础。基于案例研究,结果表明:
1)利用群智能算法和蒙特卡罗随机方法,能够有效求解随机破坏条件下野战机场体系韧性布局模型,并实现野战机场体系空间布局的快速优化;
2)合理的野战机场体系空间布局是提高资源利用效率,增强体系保障能力的基础。在4 轮次求解中,第2 轮次优化得到的机场体系节点数量最多,但其体系的作战需求满足度并不是最高,且在最不利节点失效条件下的作战需求满足度最低;
3)在不考虑敌打击失效条件下,相比于其他次优方案,野战机场体系空间布局的最优方案在体系部分节点失效后的作战需求满足度并不是最优的;
4)基于随机破坏条件下野战机场体系韧性布局模型,能够实现野战机场体系的韧性部署,即满足作战需求的同时,兼顾随机节点失效的情景。

