对称区间上和为零的三元n次幂和最大值问题研究
2023-03-11 07:11叶秀锦
中学数学研究(江西) 2023年3期
叶秀锦 臧 军
贵州省毕节市七星关区第五实验学校 (551700) 华南师范大学数学科学学院 (510631)
原题已知a,b,c∈[-2,2],a+b+c=0,求a3+b3+c3的最大值.(《数学通报》2020年2月问题2530[1])
笔者在原题的基础上推广得到两个定理,为了证明这两个结论需要用到引理1和引理2.
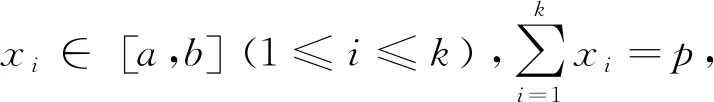

证明:引理1和引理2的证明见文献[2].
定理1 已知t>0,a,b,c∈[-t,t],a+b+c=0,l∈N*,则a2l+b2l+c2l≤2t2l,等号成立当且仅当a,b,c中有1个t,1个-t和1个0.
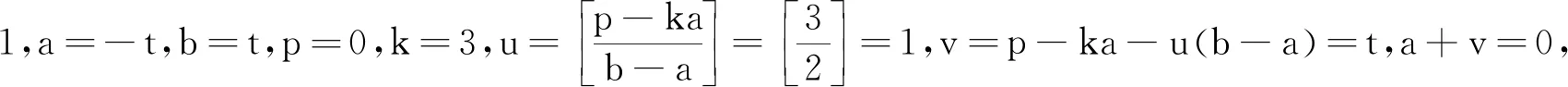

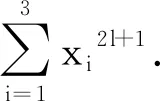

(2)如果k≥1,由引理2,那么s=0.
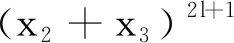
猜你喜欢
中国水土保持(2022年12期)2022-02-01
文化创新比较研究(2020年8期)2021-01-22
草原歌声(2020年2期)2020-09-25
贵州工程应用技术学院学报(2020年2期)2020-07-24
动漫星空(兴趣英语)(2017年11期)2017-02-17
小学生导刊(低年级)(2016年5期)2016-05-27
小朋友·快乐手工(2015年11期)2016-01-07
海关与经贸研究(2014年3期)2014-02-28

