基于AACGA算法的校园防疫配送路径优化
郭文强,杜正毅,李 嫔
(新疆财经大学,新疆 乌鲁木齐 830012)
1 引言
新冠疫情的出现,各省市需要采取相应措施来应对重大公共卫生突发事件。在应对的过程中,各学校所需大量防疫用品成为需要解决的问题。在此特殊环境下,如何实现疫情物资合理有效的配送,满足各高校的需求的同时节省运输成本,是本文要研究的内容。
车辆路径问题(Vehi ̄cle Routing Problem,VRP)于1959年由Dantzig等[1]提出。该问题同旅行商问题相似,都是组合优化领域中典型的NP难问题,各国学者研究至今,解决这类问题的方法主要有两类:精确算法和启发式算法。精确算法有分支定界法[2],动态规划算法等方法。精确算法能够有效的求出问题的最优解,但是随着访问客户点数量的上升,其算法复杂度会大量增加,要想解决对应问题需要花费大量的时间和费用,故逐渐被淘汰。启发式算法有人工蜂群算法[3-4],禁忌搜索算法[5],模拟退火法等[6],这类算法往往通过对过去经验的归纳推理及实验分析来解决问题,往往能够较快的得到满意解,比起精确算法更加实用,从实际决策需求的角度出发,启发式算法更加具有合理性。
蚁群算法[7-9](ant colony optimization,ACO)和遗传算法[10-12](Genetic Algorithm,GA)在解决VRP问题时使用较为广泛。蚁群算法的灵感来自于自然界中真实蚂蚁的行为,它已被证明是一种对于许多NP难问题完全可接受的启发式算法。遗传算法是一种遵循适者生存原则的进化算法,通过模拟染色体的交叉、变异等操作寻找更好的可行解来解决相应的问题。
近年来,为了弥补蚁群算法自身的缺点,提高算法的有效性,国内外学者在蚁群算法和其它算法的融合方面开展了大量的研究。例如文献[13]基于蚁群算法和遗传算法的各自特点,提出了把蚁群算法和单种群遗传算法相结合的混合算法,文献[14]提出了A*算法与蚁群算法相结合的算法,解决了冷链物流配送问题等。本文针对这种静态融合算法的局限性上,提出一种自适应蚁群遗传算法(adaptive ant colony-genetic algorithms,AACGA),以乌鲁木齐市22所学校为例,进行VRP问题的仿真模拟,最终实验结果证明,该算法在解决这类问题时能够得到更好的可行解。
2 建立问题模型
2.1 模型假设条件
根据本次研究,对疫情配送路径优化模型做出如下假设:
1)配送车辆为同一种类型的车辆;
2)配送中心(医院)只有一个,由该医院担任对所有(客户点)学校的配送任务。
3)学校和医院所在的地点和对疫情物资的需求量已知。
4)车辆在完成自己的配送任务后,由当前的配送地点驶回医院。
5)不考虑城市内出现意外突发事件。
6)车辆行驶的路程和时间成正比,即每辆车所行驶的距离决定了其配送成本。
7)一所学校不接受多台车辆的服务,车辆到达学校时要保证满足该校的需求。
8)一辆车服务的所有需求点的需求量之和不能超过车辆的额定荷载量。
2.2 符号说明
基于以上描述,本研究构建疫情期间物资配送路径优化的数学模型,首先对模型中的基本符号进行说明,表1表达了模型中基本符号的含义。

表1 模型符号说明表
2.3 优化函数的建立
首先,将配送中心编号定为0,客户点由英文字母i,j表示,决策变量的取值Xijk,yijk分别表示如下
疫情配送优化调度模型如下

(1)

(2)

(3)

(4)
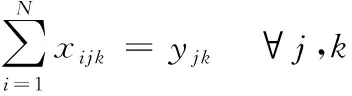
(5)
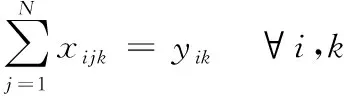
(6)
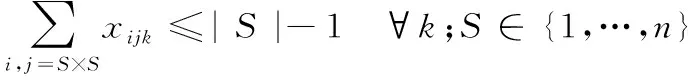
(7)
xijk=0 或 1 ∀i,j,k
(8)
yik=0 或 1 ∀i,k
(9)
式中:目标函数式(1)表示使目标函数配送成本最少;约束条件式(2)表示车载配送容量限制,约束条件式(3)表示配送车辆最大距离限制;约束条件式(4)表示每所学校保证有且只有1辆车为其服务,约束条件式(5),(6)为流量平衡约束,即每所学校及医院所进入和离开的车辆数相等;约束条件式(7)的目的是消除子回路;约束条件式(8),(9)表示决策变量的取值为0或1。
3 AACGA算法
蚁群算法最开始用于解决旅行商问题(TSP),现在也广泛用于路径优化。为了缩短蚁群算法的搜索时间,加快收敛速度,同时达到全局搜索的效果,本研究采用遗传算法与其结合的方式。自适应蚁群遗传算法是在基本蚁群算法的基础上,对其进行一定的改进,对其中的某些参数进行自适应调整后,通过在蚁群算法内部插入遗传算子,对蚁群遍历结果进行交叉变异等局部搜索操作,最后根据结果更新每条路径中的信息素浓度,从而更好的发挥蚁群算法中的信息素反馈机制;同时,蚁群算法的正反馈机制同样作用于遗传算法的初始种群,也提高了遗传算法的搜索效率。两种算法相互融合,提高了算法的寻优性能,其算法的流程图如图1所示。
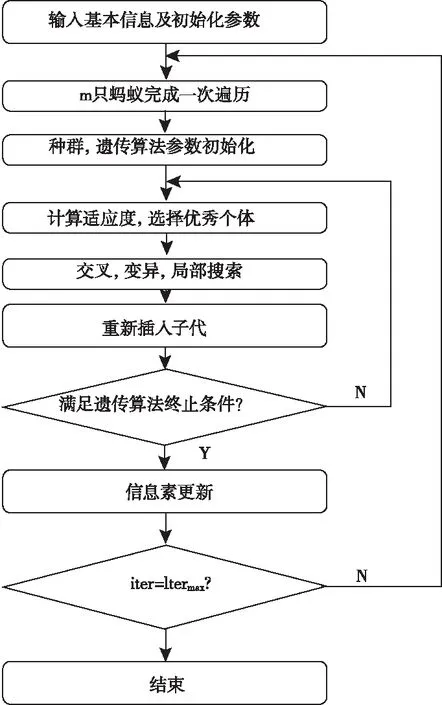
图1 算法流程图
3.1 基本蚁群算法模型构建
1)初始车辆的确定
求解前,需要先确定初始车辆的使用数目,为了避免车辆不足的情况出现,加入参数θ(0<θ<1)使其具有一定的弹性。初始车辆数m可由式(10)求得:
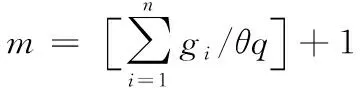
(10)
其中,[ ]表示不大于括号内数值的整数,一般来讲,条件越复杂,则约束越多,θ越小,表示一辆车能容纳的货物越少,本文中取θ=0.85。
2)状态转移概率
蚂蚁从起始点出发时,每一步都要选择要访问的对象,蚂蚁通过路径上已有的信息素浓度,以及当前位置与要访问地点的距离,来决定其下一步要访问的每个地点的概率。初始状态,各条路径上的信息素相等,即τij(0)=p(p为常数),之后蚂蚁在访问各个客户点的过程中,优秀的蚂蚁个体不断更新路径上的信息素,使得后来的蚂蚁更趋向于选择这些路径。蚂蚁的概率转移公式如式(11)所示

(11)

3) 更新信息素
蚂蚁在遍历过程中通过不断释放信息素,使得自己经过的路径信息素的含量增多,同时,路径上的信息素随着时间的推移不断挥发,从而形成信息素的不断更新。本文使用antcyclesystem模型进行更新,即蚂蚁释放的信息素含量由其经过路径的整体信息来决定,这种方法更具有全局性。更新规则为
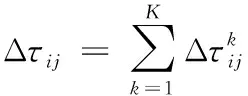
(12)
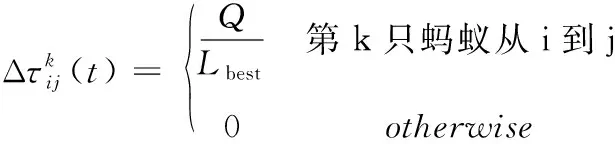
(13)
在该式中,Lbest为当次迭代中寻找到的最优路径的长度。Q为事前设定的常数,其值越大,蚂蚁所遗留的信息素浓度越高。式(14)是对当前所有路径所包含的边(i,j)的信息素更新公式如式(14)
τij(t+n)=(1-ρ)τij(t)+Δτij
(14)
ρ表示信息素挥发程度,ρ越大,信息素挥发越快。
3.2 AACGA算法构建
1)改进转移概率
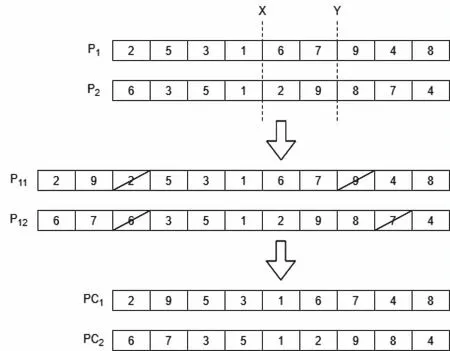
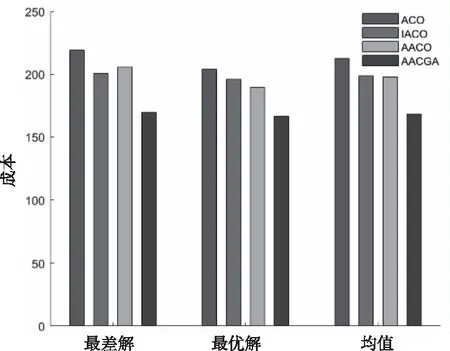
为了防止算法收敛缓慢,无法寻找的合适的解。本文引入概率转移参数r0,0 (15) 当r>r0,蚂蚁选择的方式同基本蚁群算法,利用“轮盘对赌”的方式决定下一个前往的地点;当r≤r0时,蚂蚁直接选择启发函数与信息素函数乘积最大的路径。通过这种方式使得蚂蚁能够更快的寻找到最优解。 2)自适应概率转移参数选择 如果将r0设为一个固定的值,那r0的取值如果过大或过小,都会对最后的结果产生较大影响。为了寻找到一个较为合适的r0值,本文对该值进行自适应调整,使r0随着算法的运行不断向更合适的方向变化,当算法执行过一次循环后,如果找到了更好的解,则表明在局部范围内存在着更优解,故增大r0使寻优效率增强;如果长时间所寻找到的最优解没有变化,表明算法可能陷入了局部最优解,这时需要减小r0的值,使其随机性变大,促使算法在其它区域寻找到更优秀的解,具体设置如式(16)所示 (16) Zbest为当代求得的最优解,Nmax为最优解保持不变的情况下迭代次数的上限,λ为一个[0,1]之间的参数,p为解连续停滞的代数。 3)插入遗传算子 自适应蚁群遗传算法是在蚁群算法的基础上,将遗传算子插入到算法内部,每当所有蚂蚁进行完一次周游后,运用遗传算法中的交叉,变异,局部搜索等操作再次进行优化,扩大搜索范围,最后根据产生的最优个体来更新信息素分布,从而实现全局寻优;同时,利用蚁群算法的反馈机制,反作用于遗传算法上,加强算法的搜索效率。 在所有蚂蚁对所在客户点完成一次周游后,将所有产生的解以染色体的形式表示,并对当前产生的染色体进行选择操作,首先按式(17)计算每条染色体的适应度: Fk=1/Zk (17) 由该式可知每条染色体适应度的值为其对应解的倒数,即成本越低其对应的函数值越高,之后使用轮盘对赌法选择染色体时更容易被选中。本文中采用精英保留策略,即在父代染色体中适应度排在前1/10的染色体直接遗传到子代,该策略可有效保证好的个体不会通过交叉变异等操作而丢失。 染色体的交叉过程如图2所示。对于两个染色体P1,P2随机产生两个交叉点X,Y。将各自截取的染色体片段提取出来,连接到对方染色体的头部形成新的染色体P11,P12。然后去掉原染色体中对应序号相同的染色体片段,形成最终染色体PC1, PC2。通过这种方式生成新的解,增加了解的多样性,有利于寻找到更优解。之后通过变异算子,对局部系统中少量的染色体进行变异, 通过随机交换一条染色体中的片段,使得染色体能够跳出局部最优解,从而在其它范围进行搜索,有利于解的多样性。 图2 染色体交叉示例图 以新冠肺炎疫情为例,疫情期间,新疆省医院面对各高校进行防疫物资配送服务,面向师生供应以药品,口罩等防疫为主的物资。本文选取新疆乌鲁木齐市的22所高校为例,根据防控规定,各学校所需的疫情防控物资需要统一进行配送。依据百度地图整理每个配送点的经纬度,并将这些数据通过ARCGIS转化为平面坐标。设定医院坐标为(0,0),各个高校的相对坐标及对应的每日需求补给量与该校的学生及其教职工人数有关,具体数据见表2。 表2 各学校基本信息 在AACGA算法中,含有大量参数,这些参数的取值往往会影响到最后的结果,本文经过反复实验,最终确定使用的参数如表3所示。 表3 实验参数 运用MATLABR2018b编程对该算例进行求解运算,在求解目标函数时,对4种算法分别进行测试,并将结果以图表的形式呈现出来进行比对。其中,对前文改进的前两处分别进行测试,得到改进的蚁群算法(IACO)以及自适应蚁群算法(AACO),另外两种算法为基本蚁群算法(ACO)算法和本文所研究的AACGA算法。 本次仿真中,将这四种算法分别运行10次,并记录这10次所得出的成本以及收敛代数,表4展示了这10次实验所得出的数据。通过对比分析,ACO算法所得出的配送成本最大值为219.24,最小值为204.18,平均值为212.76,比较其它算法明显看出其成本最高;IACO算法所求得的配送成本比起ACO算法有了明显的提升,最优值仅有196.12;AACO算法所得的最优解为189.63,相比较前两种算法而言更为优秀,但每次实验所求得的解相差较大,并不稳定。同时,这三种算法的收敛代数都呈现一个不稳定的状态,起伏较大。最后,对比前三者可知,AACGA算法所求得的配送成本明显降低,平均值仅有168.24,而且最佳的收敛代数明显提前,且浮动较小,并且结果稳定。图3对四种算法所得的最优解,最差解和均值以图表的形式展示,能直观的看出AACGA算法求解结果明显优于其它三种算法。 表4 运行结果比较 对照前表的相关数据,取每种算法实验中所得的最佳结果放于图4-图5中,图4中的四幅图分别对应了四种算法求得的配送方案路线图,通过对比不难看出,前三种算法求得的方案,都有着圈内交叉的现象,即车辆在行驶过程中产生了不同程度的路径交叉,耗费了多余的成本,而第四幅图中的每辆车所行驶的路径都形成了一个完整无交叉的闭环,这种方式明显更为高效,图5中也展示了这四种方案对应的收敛图,不难看出AACGA算法能够实现更为快速的收敛,也证实该算法的有效性。 图3 各算法结果对比图 针对原有算法求解车辆路径问题时的不足,本文融合了遗传算法和蚁群算法的优点,并在算法中引入了参数的自适应调整,使得种群能够更好的寻找最优解,通过选取实际问题进行多次优化仿真模拟,证明该算法能够有效降低疫情物资配送的运输成本,加快算法的收敛速度。本文算法适用于在疫情等紧急突发事件中的物资配送等业务,文章本身还有可以延伸思考的地方,为了能够更符合实际,以后将尝试更大规模的,或含有模糊限定条件的例子进行仿真。 图4 各算法配送方案最优解 图5 各算法收敛情况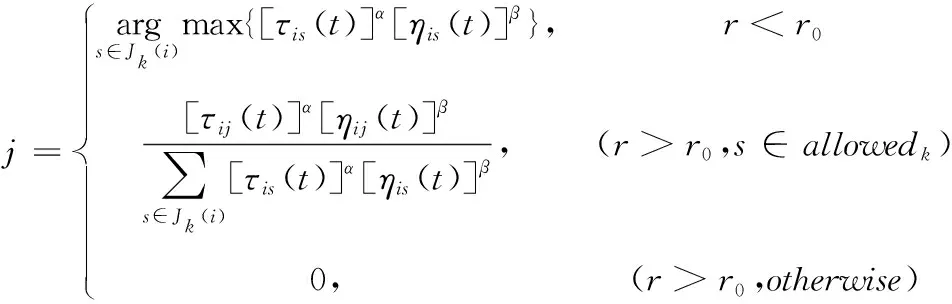
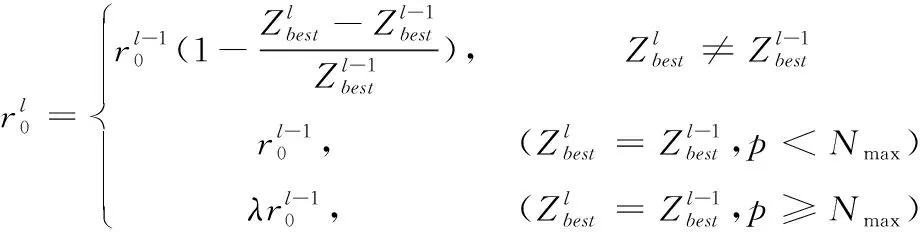
4 算例分析
4.1 背景介绍

4.2 实验参数设置

4.3 结果与讨论

5 结束语



