电子侦察卫星作战效能FASSA-SVR评估模型
陈 涛,饶世钧,洪 俊, 董 航, 张延光, 许晓波, 张 鑫
(1.海军大连舰艇学院,辽宁 大连 116000; 2.中国人民解放军91878部队,广东 湛江 524000)
0 引言
随着航天科技的发展,电子侦察卫星技术日趋成熟。在海湾战争、伊拉克战争和叙利亚战争中,美军将电子侦察卫星广泛应用于战场态势感知、远程目标指示和打击效果评估[1-2]。电子侦察卫星已经成为支援部队战术行动的重要平台。因此,研究电子侦察卫星作战效能评估,对于空间侦察技术的研发论证和战场应用具有重要的现实意义。
近年来,国内一些专家学者已经对电子侦察卫星作战效能评估开展了研究。文献[3]运用过程中心法(PFT)的效能分析方法,基于PFT建立了电子侦察卫星作战效能评估指标体系;文献[4]建立了三星时差定位精度模型,并通过该模型仿真分析了海洋监视卫星的作战效能;文献[5]对海洋监视卫星的侦察效能进行了分析,并通过卫星工具包(STK)仿真计算得到了卫星对作战区域的目标截获概率。传统的武器系统效能评估方法,如指数法、模糊综合评判法、ADC法、灰色理论法、层次分析法等,这些方法依赖于人工打分,易受主观因素的影响[6]。除此之外,上述效能评估方法缺乏自适应性和自主学习能力,无法对武器系统复杂的非线性关系进行有效映射。
支持向量回归(Support Vector Regression,SVR)是一种泛化能力较强的机器学习方法,具有较强的自适应性和自主学习能力。但在效能评估过程中,支持向量回归的惩罚因子c和核函数参数σ基本上是通过人为设定,故而存在一定盲目性。针对上述问题,本文采用萤火虫麻雀算法(FASSA)优化支持向量回归(SVR)的相关参数,得到基于FASSA-SVR的电子侦察卫星作战效能评估模型,并通过仿真实验对该模型进行了验证。
1 萤火虫麻雀算法
萤火虫算法(Firefly Algorithm,FA)是YANG受萤火虫发光行为的启发而提出的群智能优化算法,该算法具有进化过程简单、全局搜索能力强等优点[7]。在自然界中,萤火虫会通过短促而有节奏的闪光吸引异性,完成交配繁殖;有少部分萤火虫则通过闪光吸引猎物,进而捕食;此外,还有一些萤火虫将闪光作为一种预警保护的信号。
在萤火虫算法中,搜索区域中的各位置点即萤火虫个体,搜索过程即是萤火虫利用发光特性吸引其他个体向自己移动的过程。所有萤火虫均遵循扰动原理进行位置更新变化,即适应度值越好的萤火虫,对应的亮度越好,亮度较差的萤火虫会受到吸引,向亮度较好的萤火虫移动。萤火虫的相对荧光亮度算式为
I(r)=I0×e-γdi j
(1)
式中:di j为萤火虫i与萤火虫j之间的空间距离;γ为光强度吸收系数;I(r)为荧光亮度函数,当r=0时,萤火虫具有最大荧光亮度,即I0。
萤火虫扰动原理由下列两式确定,即
(2)
di=di+β(di j)×(dj-di)+α×(Nrand-1/2)
(3)
式中:β(di j)为萤火虫的吸引力函数;β0为空间距离di j=0时的吸引力;γ与di j的含义同上;di和dj分别为萤火虫i和萤火虫j所处的空间位置;α为步长因子且α∈[0,1];Nrand是在[0,1]区间上服从均匀分布的随机数值。
麻雀搜索算法(Sparrow Search Algorithm,SSA)是由XUE等在2020年提出的新型群智能优化算法,该算法受到了麻雀觅食行为和反捕食行为的启发[8]。在麻雀觅食群体中,可分为探索者、加入者和预警者3类角色。探索者在群体中负责发现食物并引导整个群体获取食物;加入者根据探索者的引导获取食物;预警者负责侦察预警,一旦发现捕食者,则立刻向群体发出警告,让所有麻雀离开危险区域飞向安全区域继续觅食。
探索者的位置更新规则为
(4)

加入者的位置更新规则为
(5)
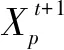
预警者的位置更新规则为
(6)

虽然麻雀搜索算法具有稳定性强、收敛速度快等优点,但也存在易陷入局部最优、收敛精度低等不足[9]。针对以上缺点,利用萤火虫算法对其进行改进。具体改进思路如下:在麻雀搜索算法完成搜索后,利用萤火虫扰动原理分别对麻雀算法中的探索者、加入者和预警者3类角色的位置进行扰动更新。若扰动后的位置优于扰动前,则更新麻雀位置;若扰动后的位置劣于扰动前,则不更新麻雀位置,并继续让麻雀进行扰动,直到搜索到最佳位置。
2 构建作战效能评估指标体系
根据文献[10]中电子侦察卫星支援海上远程精确打击作战分析,可归纳总结电子侦察卫星作战效能评估指标体系如图1所示。

图1 电子侦察卫星作战效能评估指标体系Fig.1 Evaluation index system of operation effectiveness of electronic reconnaissance satellite
1) 任务响应时间。任务响应时间是衡量电子侦察卫星能否对作战海域进行及时、有效侦察的指标,可通过舰艇编队上报需求,卫星主管部门规划侦察任务以及卫星飞行至作战海域所消耗的时间进行量化。任务响应时间越短,则卫星对于侦察任务的反应越及时,相对地,电子侦察卫星效能值也越高。
2) 连续侦察率。连续侦察率是指电子侦察卫星对作战海域进行持续侦察的能力,具体可由卫星的连续侦察时间和满足连续侦察时间条件的窗口数进行评估。连续侦察率量化数值范围为0~1,数值越大代表卫星的连续侦察能力越强,其对应的效能值也越高。
3) 定位误差。定位误差是指电子侦察卫星对目标位置进行侦察测量时,其测量位置与目标真实位置之间的误差。影响定位误差的主要因素有卫星定位体制、卫星测向精度和卫星位置误差等[11-12]。定位误差越小,则卫星对目标位置的定位也越准确,相应的效能值越高。
4) 目标识别率。目标识别率是电子侦察卫星正确判别目标属性的能力,可以通过卫星的正确识别数与总识别目标数之比确定。目标识别率的数值越大,代表卫星对目标的识别能力越强,其效能值也越高。
5) 信息传输延时。信息传输延时是指从电子侦察卫星在作战海域执行侦察任务起,到卫星主管部门将情报产品下发至舰艇编队作战平台为止,期间所消耗的总时间。信息传输延时越小,卫星的作战效能值越高。因为信息传输延时越小,则海上目标的机动散布区越小,反舰导弹捕捉到海上目标的概率也越大[10]。
3 效能评估模型
支持向量机是一种由VAPNIK等提出的可用于模式分类识别[13]和非线性回归[14]的机器学习方法。支持向量回归(SVR)是支持向量机的一种拓展,其算法的基本原理是:对于线性不可分的问题,通过核函数将样本数据映射至高维特征空间,进而在高维特征空间找到线性决策函数[15]。支持向量回归的表达式为
(7)

在核函数的选择上,对于效能评估领域,通常选择径向基函数(Radial Basis Function,RBF)作为核函数,其表达式为
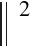
(8)
式中,σ为核函数参数。惩罚因子c和核函数参数σ直接影响着SVR模型的预测精度,c值决定了SVR模型的泛化能力,σ值决定了SVR模型的训练和预测速度[16]。因此,需要慎重选择惩罚因子和核函数参数。
本文构建的基于萤火虫麻雀算法(FASSA)优化SVR效能评估模型,其建模评估流程和运行步骤如图2所示。

图2 FASSA-SVR建模评估流程和运行步骤Fig.2 FASSA-SVR modeling evaluation process and operation steps
1) 初始化麻雀种群数量,探索者、加入者和预警者比例,迭代次数,设置预警值、觅食边界等相关参数。
2) 计算适应度值并进行排序,根据适应度值分别找到最佳位置个体和最差位置个体。
3) 运用式(4)~(6)确定麻雀种群中的探索者、加入者和预警者位置。
4) 利用式(3)模拟萤火虫扰动,对麻雀个体进行位置更新。
5) 重新计算适应度值,并更新麻雀位置。若扰动后适应度值优于扰动前,则更新麻雀位置;若扰动后适应度值劣于扰动前,则不更新麻雀位置,并重复执行步骤2)~5)。
6) 运用FASSA算法得出的惩罚因子c和核函数参数σ优化SVR模型,再运用优化后的SVR模型对归一化处理后的样本进行训练,而后进行反归一化处理,输出仿真结果。
4 仿真与分析
4.1 算法性能测试
为测试萤火虫麻雀算法的性能,选择原始麻雀搜索算法与其进行对比测试,所用标准测试函数来源于文献[17],即
(9)
(10)
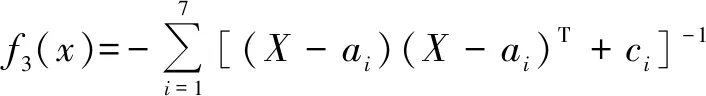
(11)
采用Matlab 2016a进行仿真实验,在测试中,将种群数量和最大迭代次数分别设置为100和500,得到萤火虫麻雀算法与麻雀搜索算法的测试结果见图3。
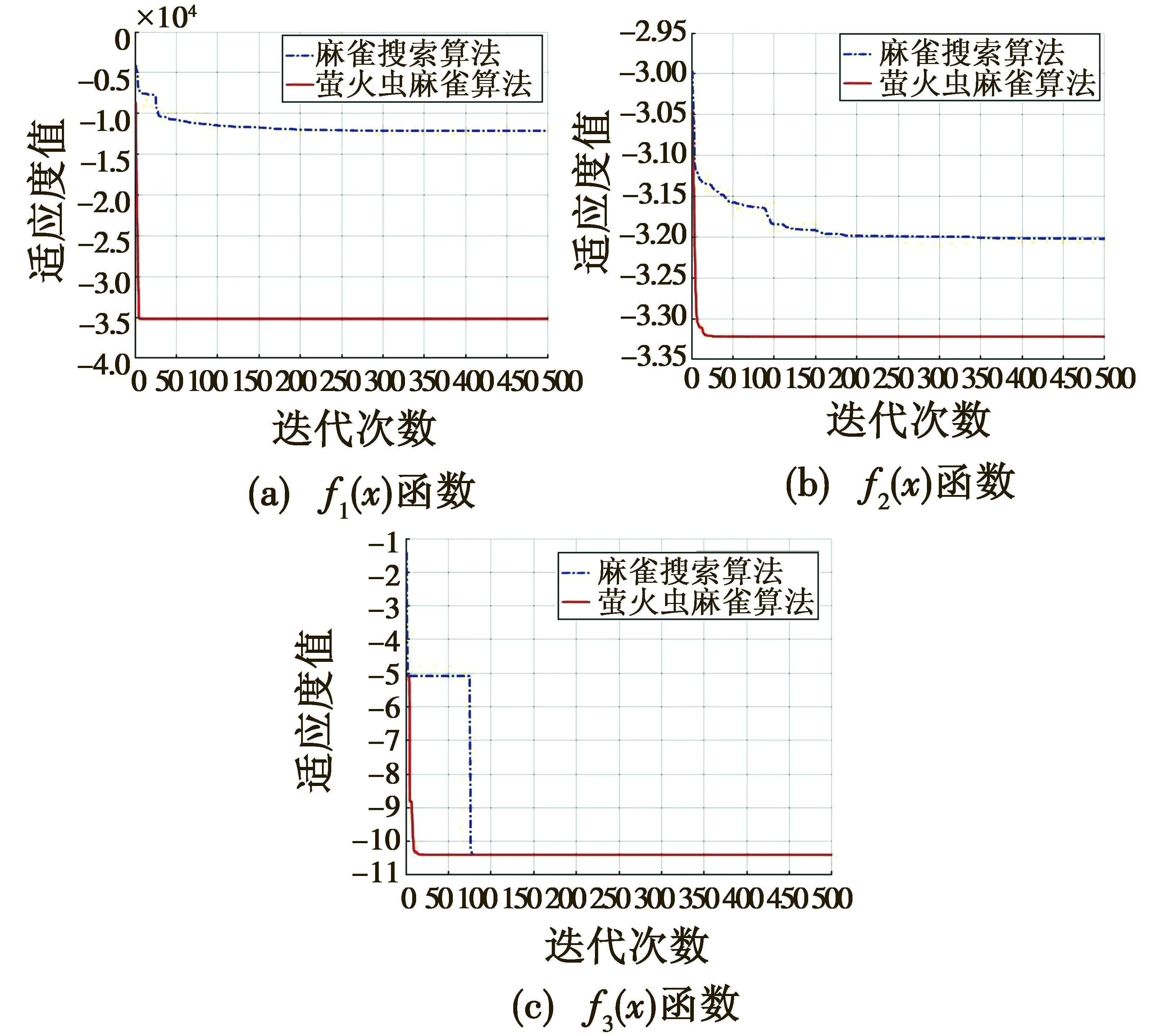
图3 性能对比图Fig.3 Performance comparison chart
从图3中可以看出,对比麻雀搜索算法,萤火虫麻雀算法的收敛精度更高,收敛速度更快,从而验证了萤火虫麻雀算法的优越性和有效性。
4.2 效能评估模型仿真
假设将任务响应时间、连续侦察率、定位误差、目标识别率和信息传输延时作为影响电子侦察卫星作战效能评估的5个主要因素,对应萤火虫麻雀算法支持向量回归(FASSA-SVR)效能评估模型的5个输入节点,FASSA-SVR模型的输出值即为电子侦察卫星的作战效能评估值。部分仿真实验数据如表1所示。
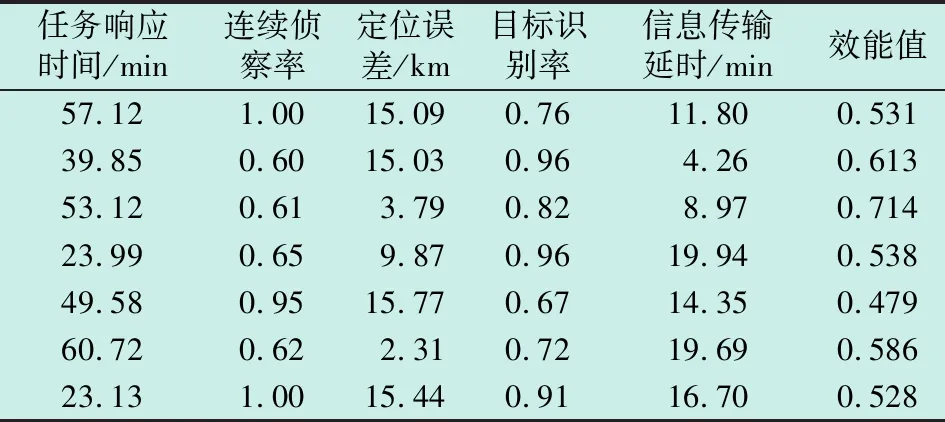
表1 部分仿真实验数据Table 1 Partial data of simulation experiment
本文通过仿真实验收集了1000组数据,选取其中的950组数据作为训练样本数据,剩下的50组数据作为预测样本数据。为验证该效能评估模型具有较强的拟合能力和较高的效能评估精度,本文还构建了支持向量回归(SVR)、遗传算法支持向量回归(GA-SVR)和自适应粒子群支持向量回归(APSO-SVR)评估模型,用于进行比较实验。为保证评估结果的客观性和公正性,在训练SVR,GA-SVR和APSO-SVR评估模型时,使用相同的训练样本数据进行训练。在训练结束后,运用同样的预测样本数据进行预测,得出了SVR,GA-SVR,APSO-SVR和FASSA-SVR评估模型的作战效能评估值以及真实效能值曲线,如图4所示。
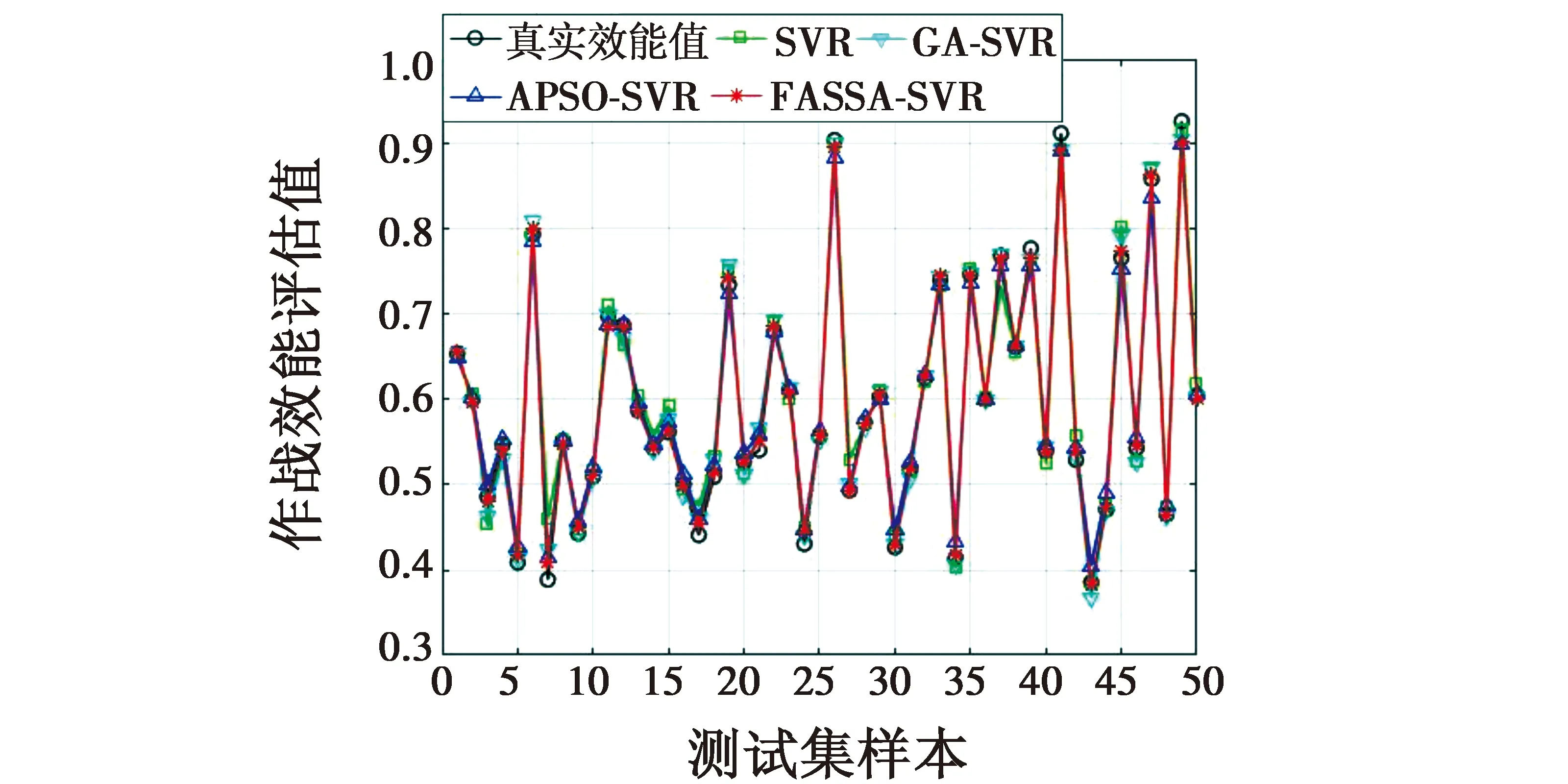
图4 作战效能值对比Fig.4 Comparison of operation effectiveness value
从图4中可以看出,FASSA-SVR评估模型输出的作战效能值比SVR,GA-SVR和APSO-SVR评估模型更接近真实值,说明FASSA-SVR模型具有更强的拟合能力。
将SVR,GA-SVR,APSO-SVR和FASSA-SVR评估模型的作战效能值分别与真实效能值进行比较,并选择平均绝对误差(MAE)、均方误差(MSE)、均方根误差(RMSE)、平均绝对百分比误差(MAPE)4项评价指标,对4个效能评估模型进行性能对比,得到了4个评估模型的输出误差、绝对误差和评价指标对比结果,分别如图5、图6和表2所示。
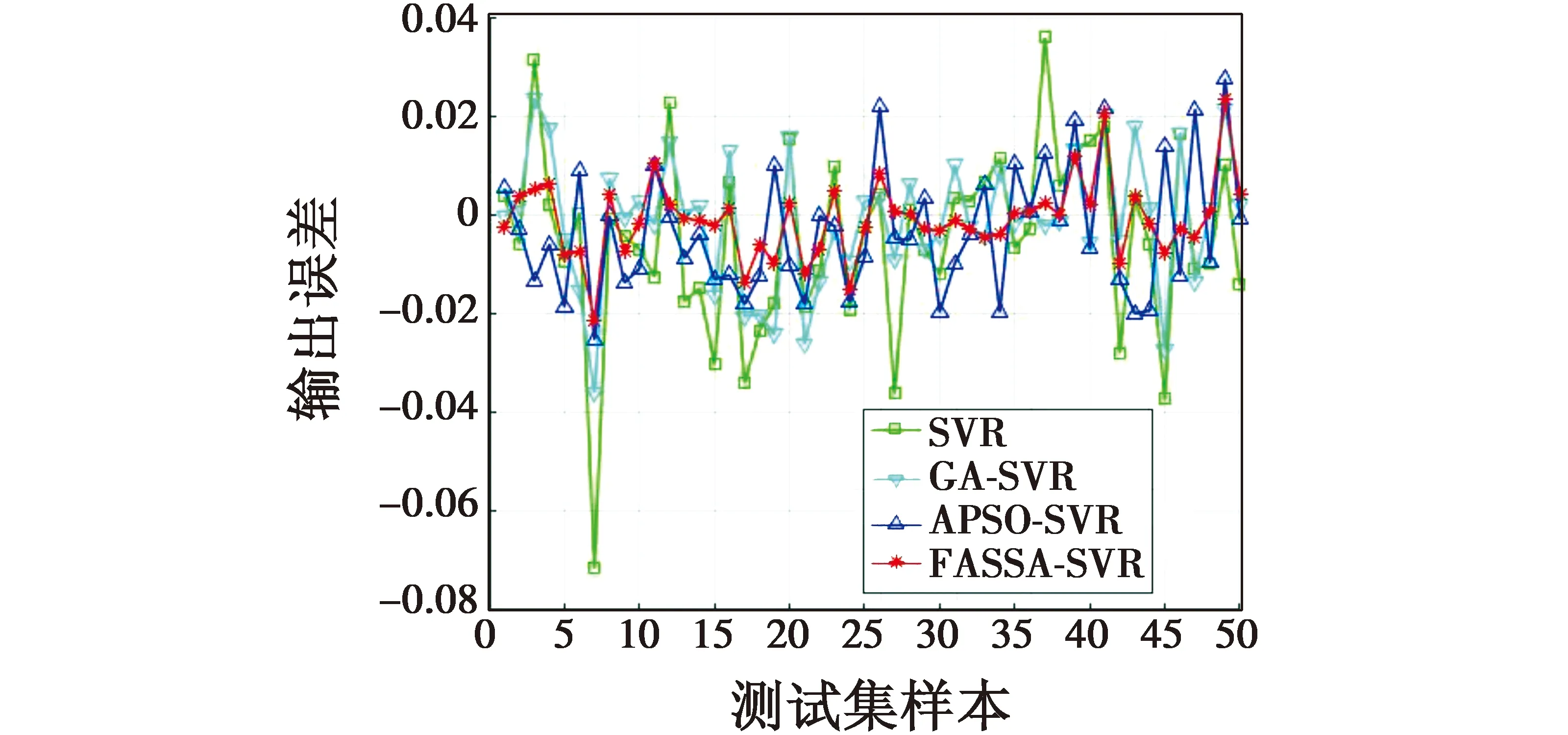
图5 输出误差Fig.5 Output error

图6 绝对误差Fig.6 Absolute error
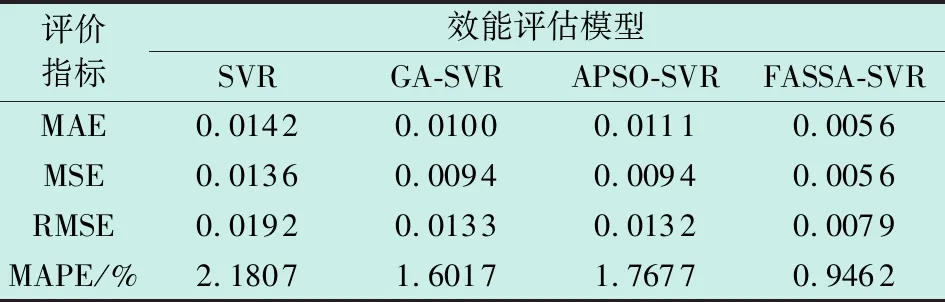
表2 4种效能评估模型性能对比Table 2 Performance comparison of four effectiveness evaluation models
从图5中可以看出,相较于SVR,GA-SVR和APSO-SVR评估模型,FASSA-SVR评估模型的输出误差更加接近于0;从图6中可以看出,FASSA-SVR评估模型的绝对误差远小于SVR,GA-SVR和APSO-SVR评估模型;由表2可知,FASSA-SVR效能评估模型的4项评价指标全面优于其他效能评估模型,进一步证明了本文所构建的模型具有更高的效能评估精度。
5 结束语
本文运用萤火虫麻雀算法优化支持向量回归,构建了基于FASSA-SVR的电子侦察卫星作战效能评估模型。仿真结果证明FASSA-SVR评估模型在拟合能力和效能评估精度方面均优于SVR,GA-SVR和APSO-SVR评估模型。基于智能群优化算法的效能评估模型具有较强的自主学习能力和自适应能力,可对复杂非线性系统的效能进行较为准确的评估,可为今后设计电子侦察卫星作战效能评估系统提供一定参考。

