非线性能量收集认知无线电网络的次用户吞吐量最大化方案
葛海江,贾宁,池凯凯,陈云志
非线性能量收集认知无线电网络的次用户吞吐量最大化方案
葛海江1,贾宁1,池凯凯2,陈云志1
(1. 杭州职业技术学院信息工程学院,浙江 杭州 310018;2. 浙江工业大学计算机科学与技术学院,浙江 杭州 310023)
针对一对主用户和对次用户构成的认知无线电网络(cognitive radio network,CRN),研究了非线性能量收集的认知无线电网络的次用户吞吐量最大化问题。具体来说,对于考虑次用户发射器(secondary transmitter,ST)电路功率的情况,首先将主用户吞吐量需求下的次用户吞吐量最大化(secondary throughput maximization,STM)问题建模为一个非线性优化问题,然后将它转化成凸优化问题,最后提出一种联合使用黄金分割和二分法的低复杂度算法,获得主用户发射器(primary transmitter,PT)能量传输和次用户信息传输的最优时间分配以及主用户发射器的最优发射功率。对于忽略次用户发射器电路功率的情况,首先证明次用户吞吐量最大化问题的凸特性,然后设计了一个更高效的算法来求解。仿真结果表明,相比等时间分配方案和链路增益优先级方案,提出的设计算法能显著提升次用户吞吐量。
认知无线电网络;非线性能量收集;次用户吞吐量最大化;低复杂度;凸优化
0 引言
近10年来,随着无线设备和服务需求的不断增长,有限的频谱资源已经成为一种稀缺资源。然而,美国联邦通信委员会(Federal Communications Commission,FCC)调查研究显示,现有的频谱资源未被充分利用(授权频谱的利用率范围为15%~85%)[1]。这种现象使得认知无线电(cognitive radio,CR)技术应运而生,该技术允许非授权用户,即次用户(secondary user,SU),在不降低主用户性能的情况下,有机会访问授权用户的授权频谱[2]。 获得授权的用户被称为主用户(primary user,PU)。除了频谱利用率不足带来的挑战,随着全球能源的不断消耗,针对能源短缺的挑战,具有可再生能源(如太阳能[3]、风能[4]和射频信号[5]等)的绿色网络[6]吸引了许多学者的关注。
为了应对上述两个挑战,能量收集认知无线电网络(energy-harvesting cognitive radio network,EH-CRN)是一种很有前途的方法,可以有效地提高能量效率和频谱效率[7-9]。一方面,从环境可再生能源中获取的能量可以缓解CRN的能量限制,这是因为它提供了永久性的能源供应,而不需要人为地充电或更换电池;另一方面,机会频谱的接入可以提高CRN的频谱效率和吞吐量。
针对EH-CRN的相关研究[7-21]大多集中在可再生资源驱动的CRN方面。对于仅有一条主链路和一条次链路的CRN,Wang等[10]通过优化PU和SU之间的时间分配来最大化SU的吞吐量,Zheng等[11]通过分析电池充电和能量收集的影响来最大化次用户吞吐量。Pratibha等[12]通过优化传输时间和收集时间来最大化次用户吞吐量。在无人机中继协作下,Li等[13]通过优化中继的发射功率和次用户发射器(secondary transmitter,ST)的发射功率实现次用户吞吐量最大化(secondary throughput maximization,STM)。对于具有多对SU的EH-CRN,Xu等[14]研究了PU和SU之间的时间和功率分配,以最大限度地提高多跳CRN的端到端吞吐量。Wang等[15]在干扰功率和最小吞吐量需求的约束下,通过优化发射功率分配来最大化次用户平均吞吐量。Kalamkar等[16]通过协同优化SU的时间和能量分配来实现SU总吞吐量最大化。Liu等[17]提出了一种联合优化子信道、功率和时间分配的算法,以实现EH-CRN的总吞吐量最大化。Zheng等[18-19]通过研究协同频谱感知以及PU和SU之间的最优时间分配来实现EH-CRN的总吞吐量最大化。Xu等[20]通过联合优化功率控制和时间分配来实现PU的吞吐量最大化。Jafari等[21]研究了全双工和半双工模式下SU的最优时间和能量分配,使得SU吞吐量最大化。
此外,具有理想硬件的EH-CRN[22]只考虑发射功率而没有考虑电路本身的功率,因此在实际网络设计中可能是不准确的。为此,研究人员对包含电路功率的EH-CRN做了一些相关的研究。在满足SU最小体验质量需求的情况下,Yang等[23]研究了带有固定电路功率和动态电路功率的EH-CRN的最优发射功率分配。Xu等[20]在考虑PU和SU电路功率的情况下,研究了协作CRN中无线供能PU的吞吐量最大化。
综上所述,对EH-CRN的研究都基于线性能量收集模型,然而,实际的射频(radio frequency,RF)能量收集电路的转换效率会随着RF输入功率的变化而变化[24-25]。具体地,当能量收集电路的RF输入功率不断增加时,电路的转换效率将先增大后减小。当RF输入功率增大到一定值时,电路将进入饱和状态,收集电路的输出功率将维持不变。因此,传统的线性能量收集模型并不能真实地反映实际RF能量收集电路的非线性特性。研究人员针对非线性能量收集的CRN做了一些相关的研究工作。Wang等[26]通过联合优化能量收集时间、信道分配和发射功率实现非线性能量收集CRN的次用户总吞吐量最大化。针对基于非线性EH模型和非正交多址接入(non-orthogonal multiple access,NOMA)的CRN,在最小传输速率和最大干扰功率的约束下,Wang等[27]通过优化发射功率实现每个SU的收集能量最大化。Prathima等[28]通过优化SU能量收集时间、PU与SU双向的数据传输时间以及SU的接收功率实现EH-CRN的总吞吐量最大化。
鉴于此,研究基于非线性能量收集且考虑用户电路功率约束的EH-CRN的次用户吞吐量最大化问题具有重要意义。本文的创新工作主要体现在以下两个方面:(1)在EH-CRN中,首次对非线性能量收集、SU的电路功率以及主用户吞吐量的需求进行了整体的考虑,实现了次用户吞吐量的最大化,使得研究更加符合实际的需求;(2)对于SU是否有电路功率的情况,本文分别设计了低复杂度的算法,实现了EH-CRN的STM,相比等时间分配方案或链路增益优先级方案,所设计的算法获得的次用户吞吐量更大。
在非线性EH-CRN中,主用户发射器(primary transmitter,PT)在每个时隙开始时都具有一定的能量。每个初始能量为零的ST都没有固定的电源,完全由从主用户信号中获取的RF能量进行供电。由于SU中结合了能量收集的功能,PU和SU之间的时间分配变得更加复杂,因此,对于非线性EH-CRN,本文将联合优化PU和SU之间的时间分配,实现SU电路功率约束下的EH-CRN的STM。
1 系统模型和吞吐量建模
本节首先描述EH-CRN系统模型,然后进一步介绍时序模型,最后分别给出PU和SU的吞吐量建模方法。
1.1 系统模型
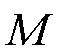
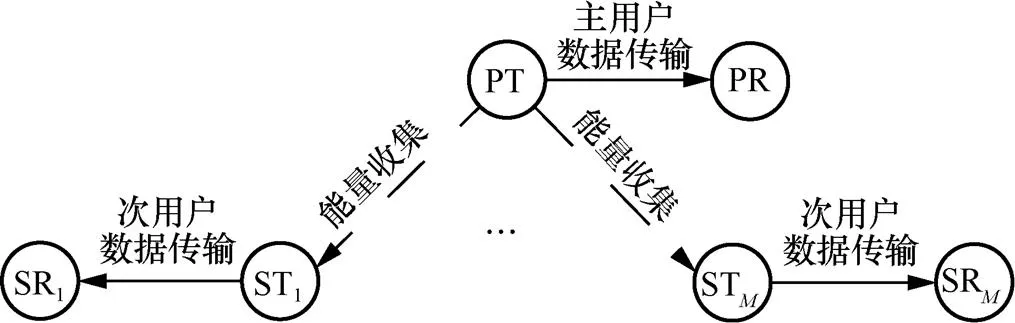
图1 带有一对PU和M对SU的EH-CRN示意图
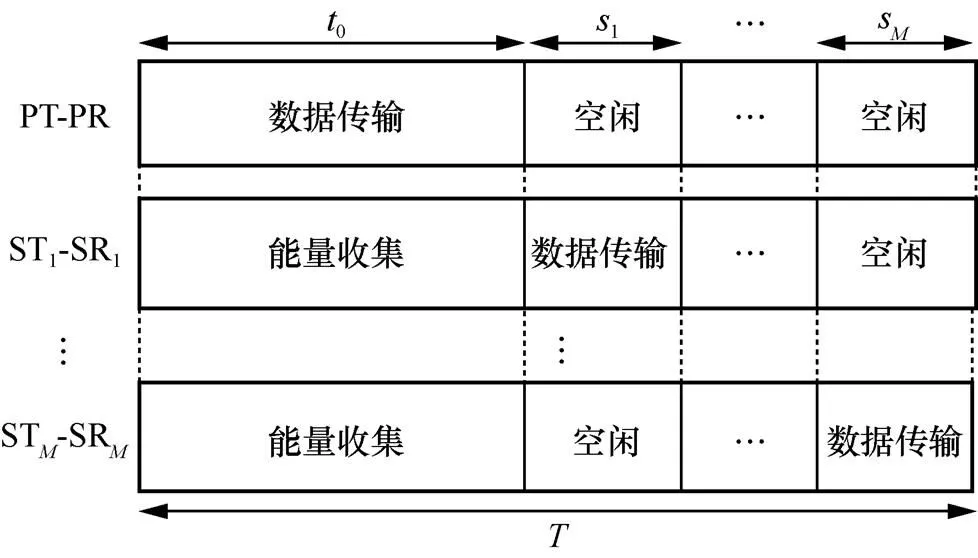
图2 基于TDMA的EH-CRN的HTT协议
1.2 时序模型
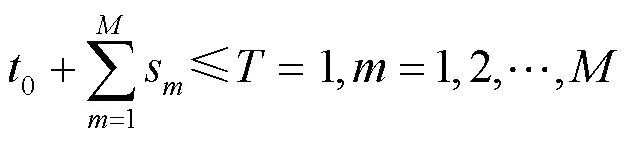
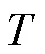
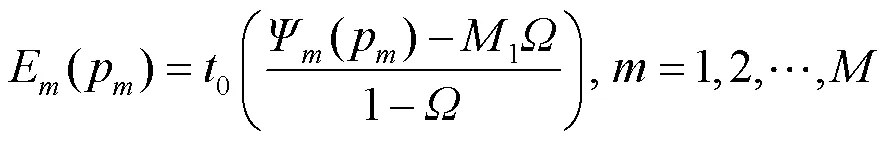
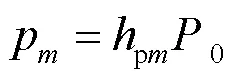
1.3 吞吐量建模
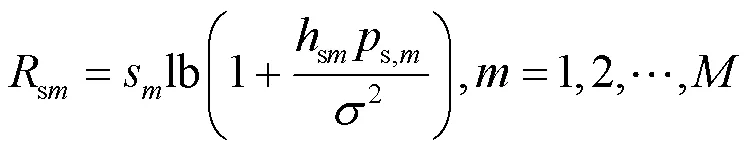
同样地,PT-PR的吞吐量,单位为bit/(s·Hz),可表示为:
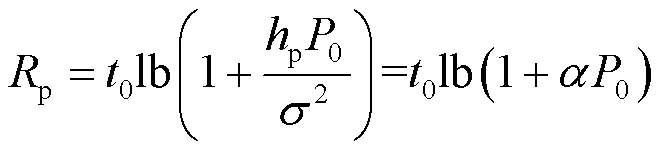
2 满足PU最小吞吐量需求的EH-CRN的STM高效算法
对于具有PU最小吞吐量需求的EH-CRN的STM,首先引入一些定理,将STM问题简化为一个凸优化问题,然后提出一种高效的算法来求解。
2.1 问题建模
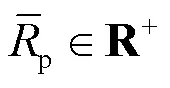
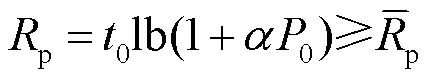
因此,基于PU最小吞吐量需求的STM问题被建模为:
(P1):
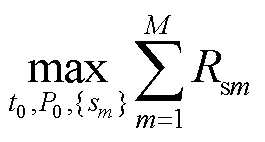
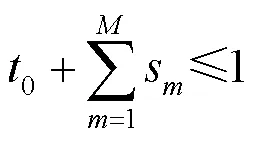
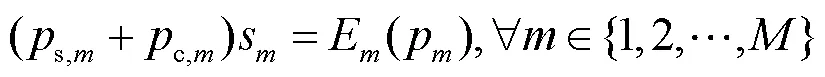
证明 请参考文献[31]的定理1。
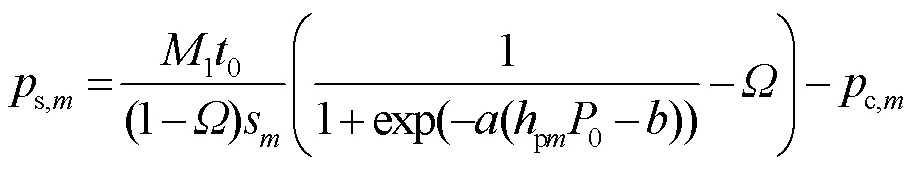
将式(8)代入式(4),可得:
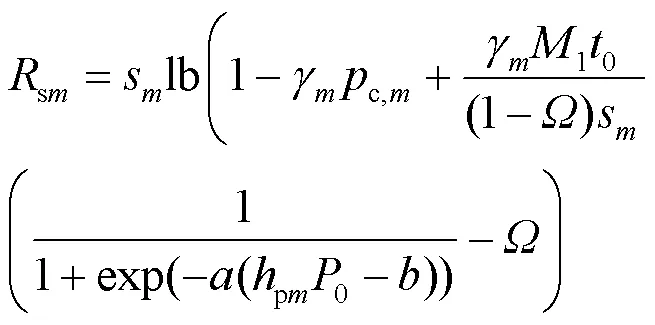
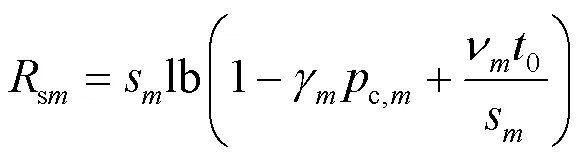
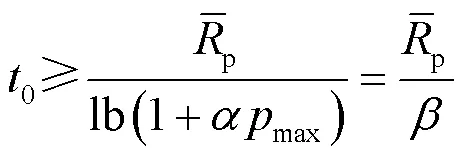
基于定理1,问题(P1)被转换为如下问题。
(P1.1):
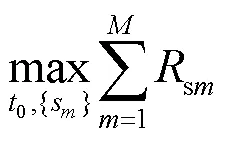
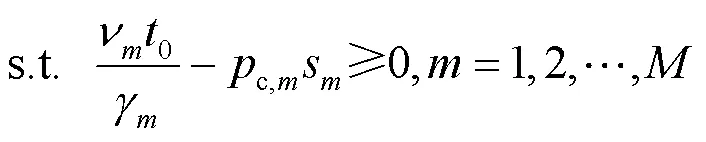
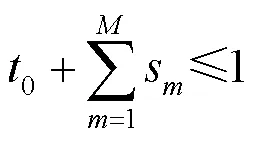
定理2 问题(P1.1)是一个凸优化问题。
证明 请参考文献[32]的定理3.2。
根据定理3,问题(P1.1)能被转换为如下问题。
(P1.2):
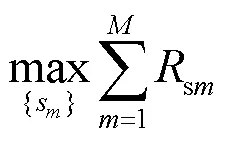
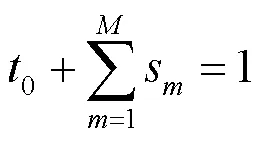
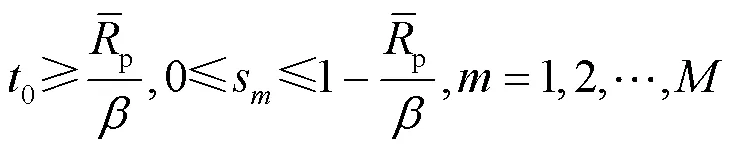
定理4 问题(P1.2)是一个凸优化问题。
定理4的证明跟定理2的证明类似,简略起见,这里省略证明过程。
接下来,定义次用户的最大吞吐量为:
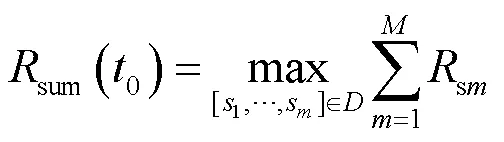
其中,是满足式(13)中的所有约束条件的可行集合,即是给定下可获得的最大次用户吞吐量。的凹函数特性如图3所示,是关于的凹函数,这是因为是凸函数的无限集上的逐点上确界[33]。其中,是获得最优解时的取值。
2.2 STM问题的高效算法
本节首先引入一些定理,将STM问题简化为如下两个步骤,从而解决问题(P1.2)。
为了完成上述两个步骤,这里引入如下定理。
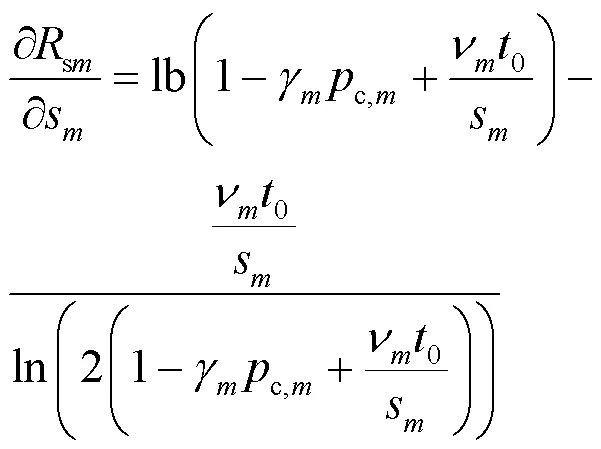
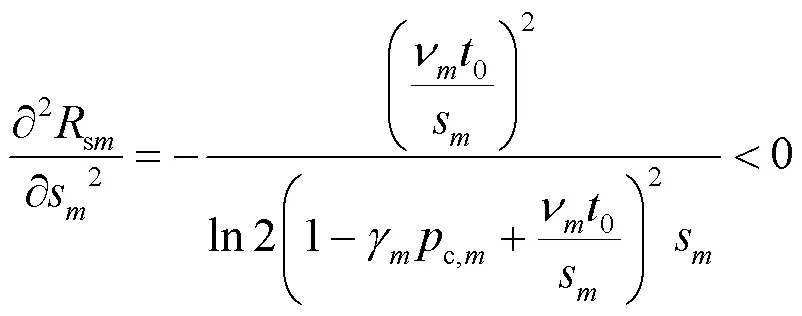
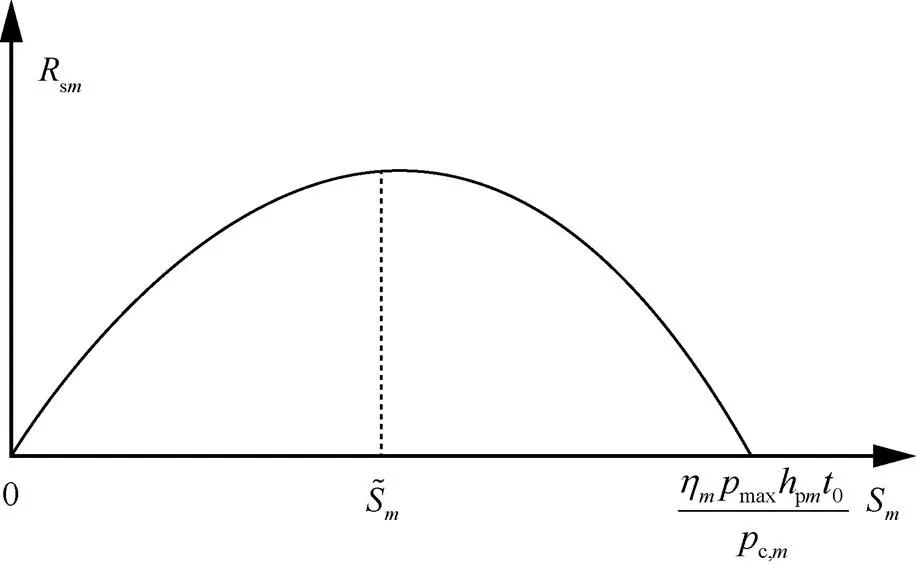
图4 给定时的凹函数特性
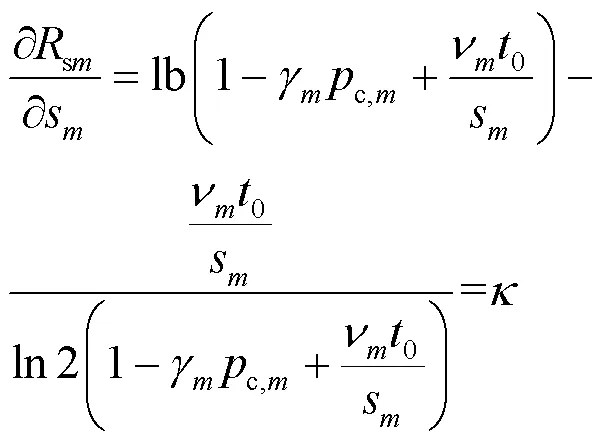
(2)repeat
(4) repeat
(14)repeat
(2)repeat
下面简要分析所提算法的计算复杂度。
3 不考虑电路功率的场景
目前,无线电网络传感节点的电路功率可以达到非常低。例如,在传感节点中广泛使用的MSP430微控制器功率只有几百微瓦。 此外,随着工业的发展,电路功率将越来越低。因此,与用于数据传输的功率相比,电路功率可能可以忽略不计。 本节提出了一个更高效的算法来实现电路功率可忽略场景下EH-CRN的次用户吞吐量最大化。
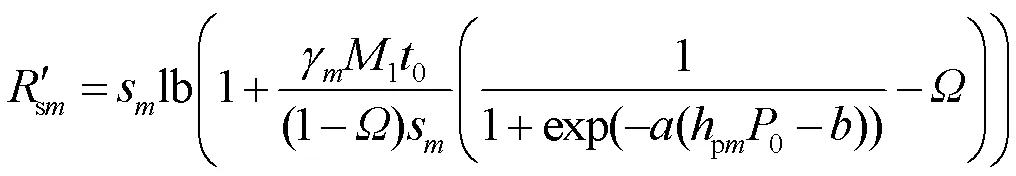
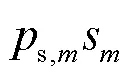
(P2):
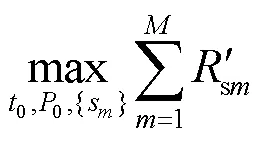
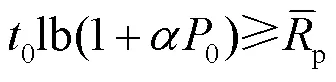
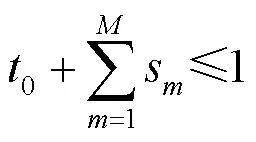
为了得到问题(P2)的最优解,引入如下定理。
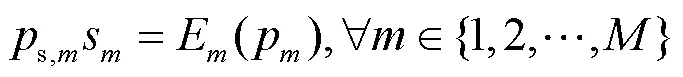
证明方法类似于定理1的证明,这里略去。
(P2.1):
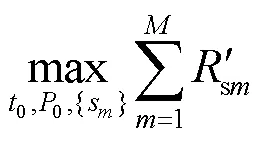
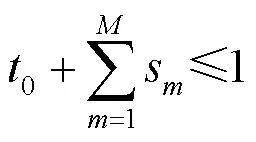
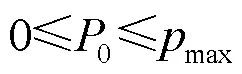
证明方法类似于定理3的证明,这里略去。
接下来,可以得到:
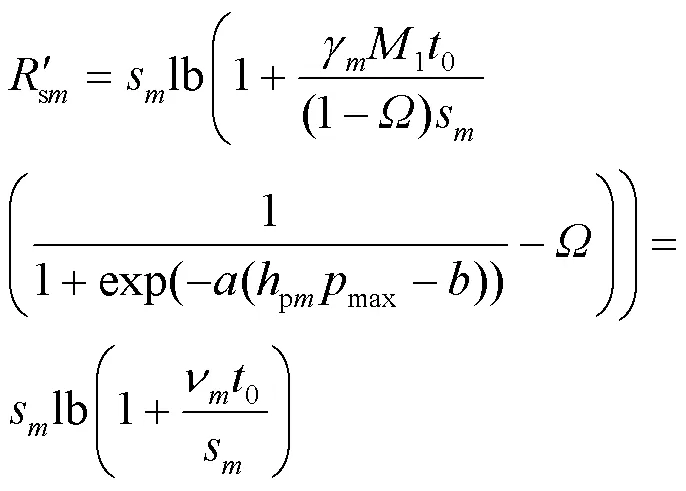
根据定理8和定理9,问题(P2.1)可以被重新建模为:
(P2.2):
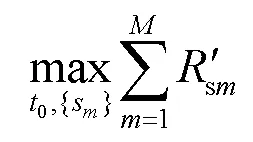
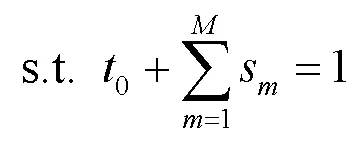
定理10 问题(P2.2)是一个凸优化问题。
证明方法类似于定理4的证明,这里略去。
凸优化问题(P2.2)可分两步求解。
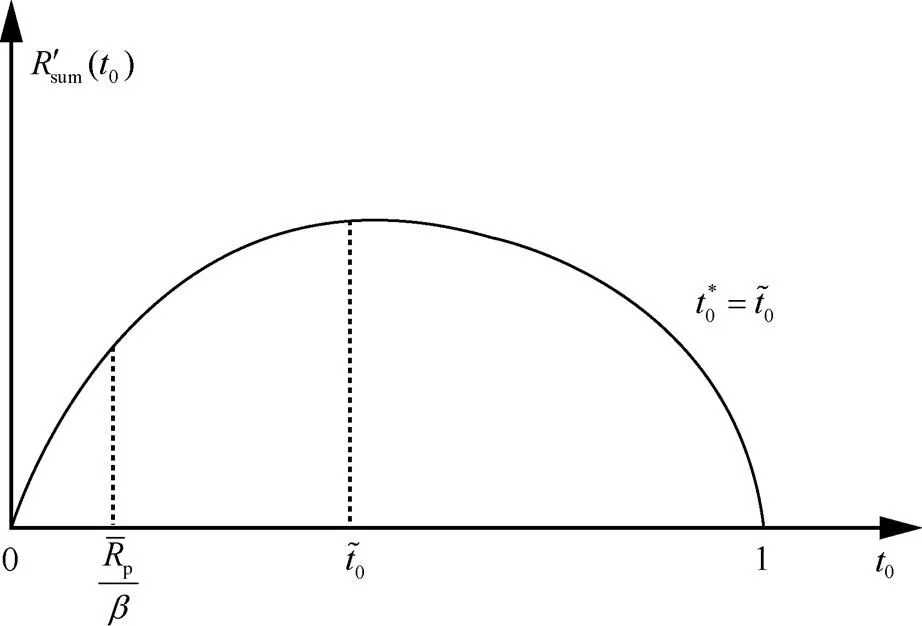
图5 给定时的凹函数特性
(P2.3):
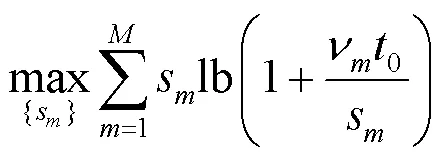
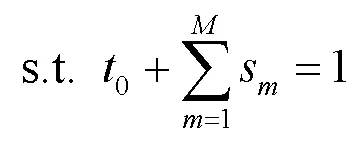
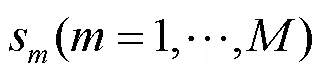
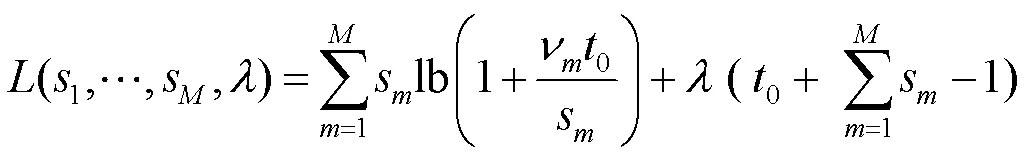
然后,给出对偶问题:
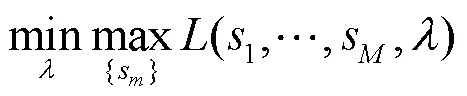
可以知道,凸优化问题的原解和对偶解的最优性的充要条件是KKT(Karush-Kuhn-Tucker)条件,具体为:
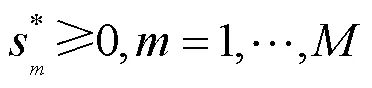
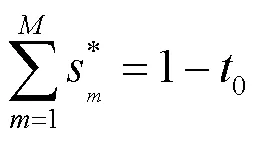
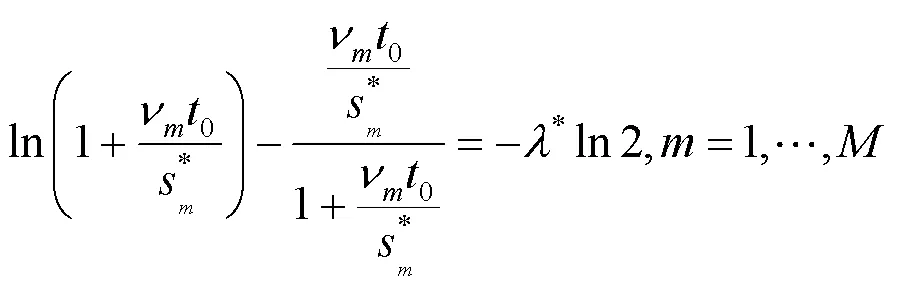
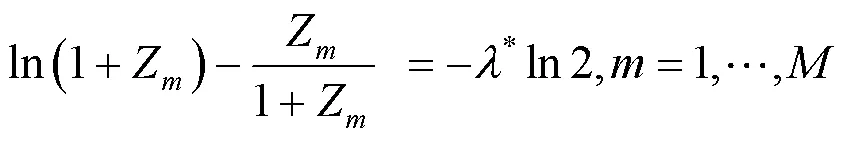
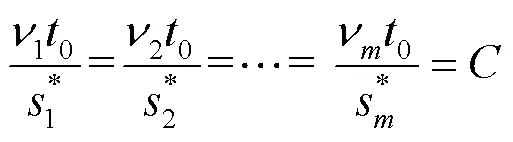
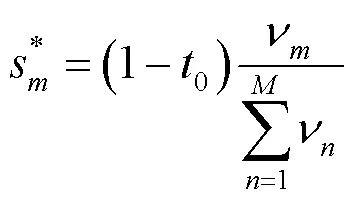
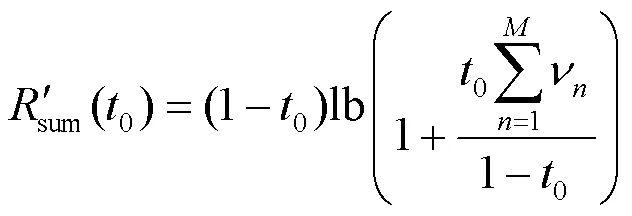
(2)repeat
4 仿真结果与分析
4.1 SU的最大吞吐量与电路功率的关系
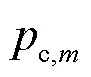
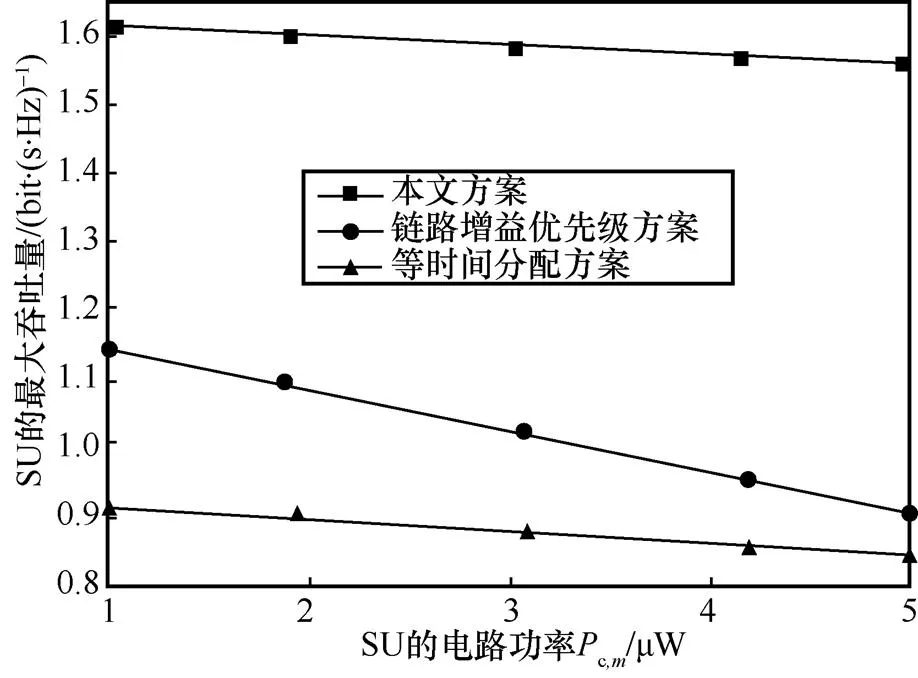
图6 3种方案的SU的最大吞吐量与电路功率的关系
4.2 SU最大吞吐量与SU数量的关系
0=0.2 W、p=6 bit·(s·Hz)-1时,SU有无电路功率情况下3种方案的SU最大吞吐量与SU数量的关系如图7所示。
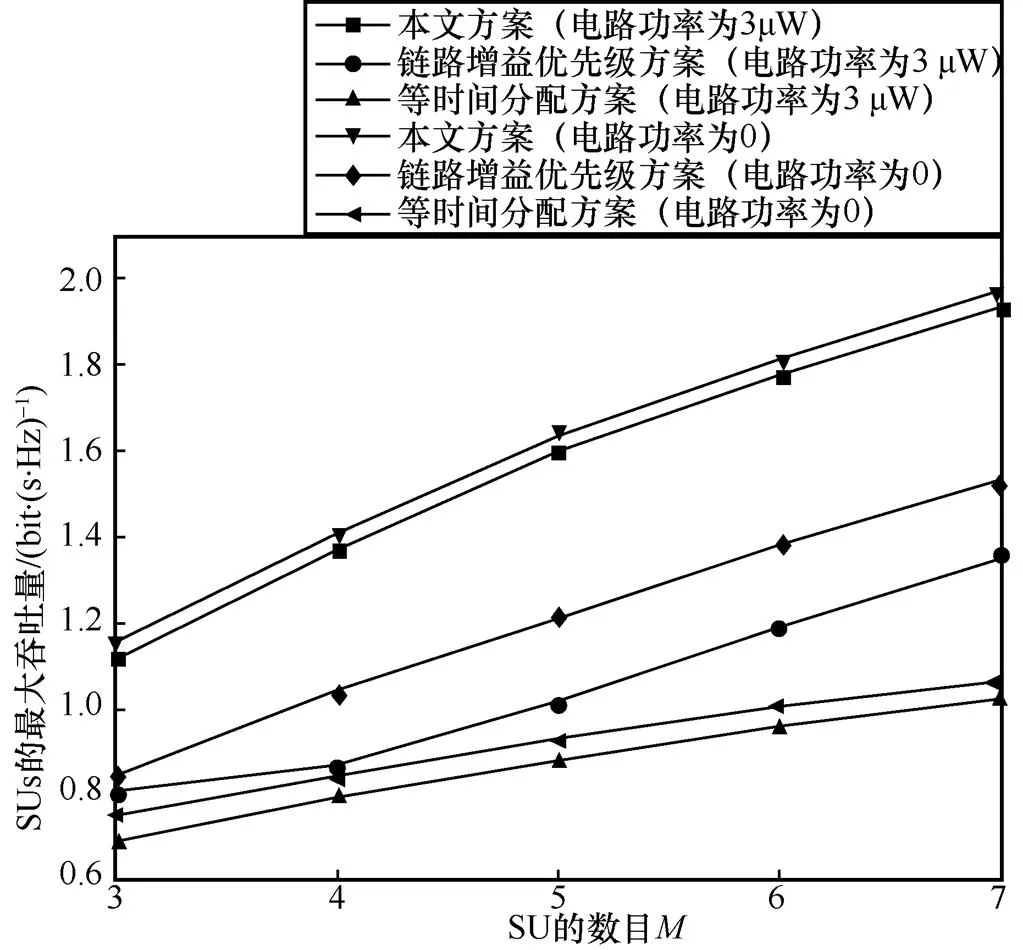
图7 SU有无电路功率情况下3种方案的SU最大吞吐量与SU数量的关系
从图7可以得出如下结论。
首先,不管SU是否有电路功率,3种方案的SU最大吞吐量都会随着SU数量的增大而增大。这是因为随着SU数量的增大,SU的总采集能量增加,因此能获得一个更大的SU吞吐量。
其次,SU有电路功率情况下3种方案的SU最大吞吐量比SU无电路功率情况下的SU最大吞吐量小。这是因为SU有电路功率时,SU实际可用于数据传输的能量减少,从而导致SU最大吞吐量变小。
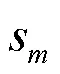
4.3 SU最大吞吐量和PU最小吞吐量需求的关系
=5、0=0.2 W时,SU有无电路功率情况下3种方案的SU最大吞吐量和PU最小吞吐量需求的关系如图8所示。
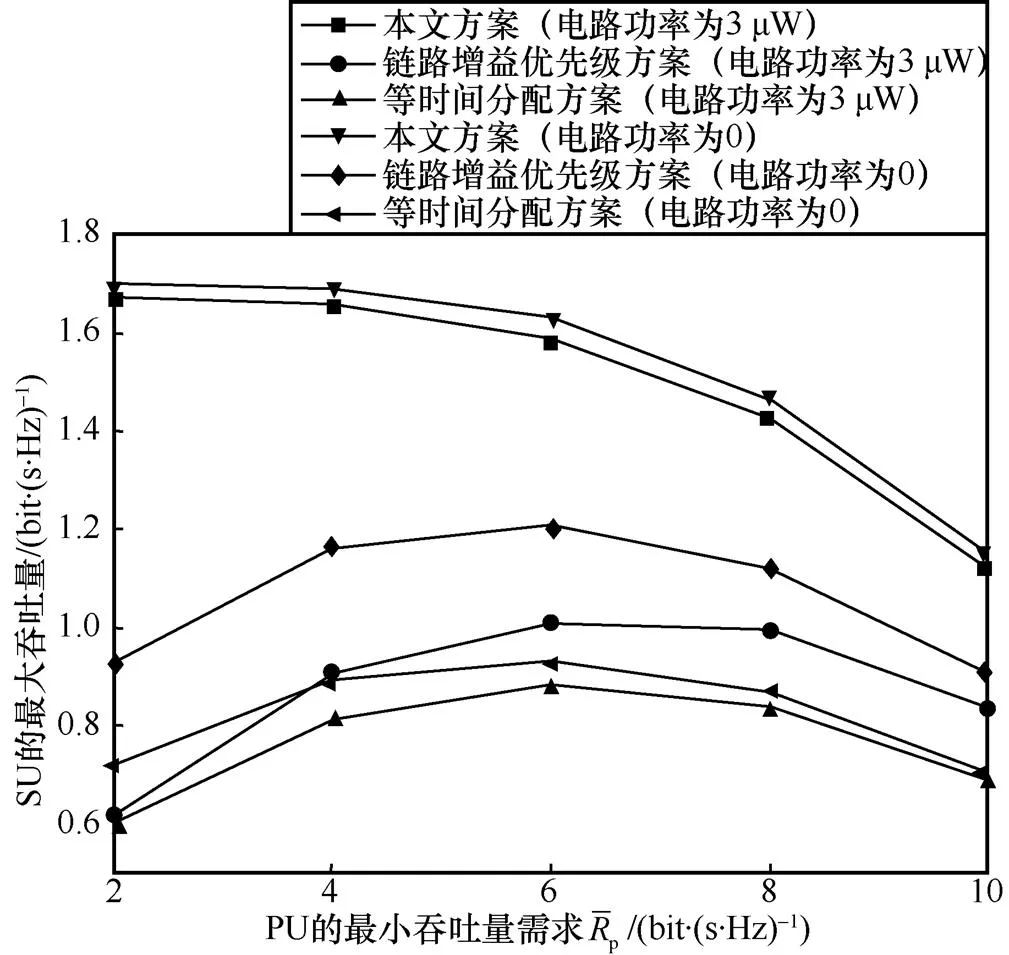
图8 SU有无电路功率情况下3种方案的SU最大吞吐量与PU最小吞吐量需求的关系
从图8可以得出如下结论。
首先,随着PU最小吞吐量需求的增加,无论SU有无电路功率,本文方案的SU最大吞吐量都减小。原因如下:随着PU最小吞吐量需求的增加,在PT的发射功率不变的情况下,PT需要花费更多的时间来满足PU最小吞吐量要求。因此,分配给SU完成数据传输的时间变少,从而使得SU的最大吞吐量减少。
其次,无论SU有无电路功率,其他两种方案的SU最大吞吐量都比本文方案小,同时链路增益优先级方案要优于等时间分配方案。这是因为本文方案的SU最大吞吐量是最优解,而等时间分配方案和链路增益优先级方案的SU最大吞吐量不是问题的最优解;同时,相比等时间分配方案,链路增益优先级方案具有更合理的时间分配。SU无电路功率情况下3种方案的SU最大吞吐量都比SU有电路功率情况下的SU最大吞吐量大。原因与第4.2节第二点的分析类似。
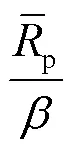
5 结束语

[1] FCC. Spectrum policy task force, report of the spectrum efficiency working group[R]. 2002.
[2] LIU X Y, ZHENG K C, LIU X Y, et al. Hierarchical cooperation improves delay in cognitive radio networks with heterogeneous mobile secondary nodes[J]. IEEE Transactions on Mobile Computing, 2019, 18(12): 2871-2884.
[3] GAUTAM N, MOHAPATRA A. Efficiently operating wireless nodes powered by renewable energy sources[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(8): 1706-1716.
[4] TAN Y K, PANDA S K. Self-autonomous wireless sensor nodes with wind energy harvesting for remote sensing of wind-driven wildfire spread[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(4): 1367-1377.
[5] CHEN X H, LIU Y, CAI L X, et al. Resource allocation for wireless cooperative IoT network with energy harvesting[J]. IEEE Transactions on Wireless Communications, 2020, 19(7): 4879-4893.
[6] KANSAL A, SRIVASTAVA M B. An environmental energy harvesting framework for sensor networks[C]//Proceedings of the 2003 International Symposium on Low Power Electronics and Design. New York: ACM Press, 2003: 481-486.
[7] HU H, ZHANG H, LIANG Y C. On the spectrum- and energy-efficiency tradeoff in cognitive radio networks[J]. IEEE Transactions on Communications, 2016, 64(2): 490-501.
[8] ZHANG W S, WANG C X, CHEN D, et al. Energy-spectral efficiency tradeoff in cognitive radio networks[J]. IEEE Transactions on Vehicular Technology, 2016, 65(4): 2208-2218.
[9] XU X M, YANG W W, CAI Y M, et al. On the secure spectral-energy efficiency tradeoff in random cognitive radio networks[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(10): 2706-2722.
[10] WANG Y C, LIU K J R. Statistical delay QoS protection for primary users in cooperative cognitive radio networks[J]. IEEE Communications Letters, 2015, 19(5): 835-838.
[11] ZHENG K C, LIU X Y, ZHU Y H, et al. Impact of battery charging on spectrum sensing of CRN with energy harvesting[J]. IEEE Transactions on Vehicular Technology, 2020, 69(7): 7545-7557.
[12] PRATIBHA, LI K H, TEH K C. Optimal spectrum access and energy supply for cognitive radio systems with opportunistic RF energy harvesting[J]. IEEE Transactions on Vehicular Technology, 2017, 66(8): 7114-7122.
[13] LI H Q, ZHAO X H. Throughput maximization with energy harvesting in UAV-assisted cognitive mobile relay networks[J]. IEEE Transactions on Cognitive Communications and Networking, 2021, 7(1): 197-209.
[14] XU C, ZHENG M, LIANG W, et al. End-to-end throughput maximization for underlay multi-hop cognitive radio networks with RF energy harvesting[J]. IEEE Transactions on Wireless Communications, 2017, 16(6): 3561-3572.
[15] WANG Y Y, ZHAO X H, LIANG H. Throughput maximization-based optimal power allocation for energy-harvesting cognitive radio networks with multiusers[J]. EURASIP Journal on Wireless Communications and Networking, 2018, 2018(1): 1-10.
[16] KALAMKAR S S, JEYARAJ J P, BANERJEE A, et al. Resource allocation and fairness in wireless powered cooperative cognitive radio networks[J]. IEEE Transactions on Communications, 2016, 64(8): 3246-3261.
[17] LIU Z X, ZHAO M Y, YUAN Y Z, et al. Subchannel and resource allocation in cognitive radio sensor network with wireless energy harvesting[J]. Computer Networks, 2020(167): 107028.
[18] ZHENG K C, LIU X Y, ZHU Y H, et al. Total throughput maximization of cooperative cognitive radio networks with energy harvesting[J]. IEEE Transactions on Wireless Communications, 2020, 19(1): 533-546.
[19] LIU X Y, ZHENG K C, CHI K K, et al. Cooperative spectrum sensing optimization in energy-harvesting cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2020, 19(11): 7663-7676.
[20] XU D, ZHU H B. Sum-rate maximization of wireless powered primary users for cooperative CRNs: NOMA or TDMA at cognitive users?[J]. IEEE Transactions on Communications, 2021, 69(7): 4862-4876.
[21] JAFARI R, MAHDAVI M, FAZEL M S. Sum-throughput maximization of secondary users in an in-band full-duplex cognitive wireless powered communication network[J]. IEEE Systems Journal, 2020, 14(2): 2109-2120.
[22] NGO H Q, LARSSON E G, MARZETTA T L. Energy and spectral efficiency of very large multiuser MIMO systems[J]. IEEE Transactions on Communications, 2013, 61(4): 1436-1449.
[23] YANG W W, ZHAO X H. Resource allocation in two-way OFDM-based cognitive radio networks with QoE and power consumption guarantees[J]. EURASIP Journal on Wireless Communications and Networking, 2017, 2017(1): 1-14.
[24] BOSHKOVSKA E, NG D W K, ZLATANOV N, et al. Practical non-linear energy harvesting model and resource allocation for SWIPT systems[J]. IEEE Communications Letters, 2015, 19(12): 2082-2085.
[25] CHEN Y F, SABNIS K T, ABD-ALHAMEED R A. New formula for conversion efficiency of RF EH and its wireless applications[J]. IEEE Transactions on Vehicular Technology, 2016, 65(11): 9410-9414.
[26] WANG Y J, WANG Y H, ZHOU F H, et al. Resource allocation in wireless powered cognitive radio networks based on a practical non-linear energy harvesting model[J]. IEEE Access, 2017(5): 17618-17626.
[27] WANG Y H, WU Y H, ZHOU F H, et al. Multi-objective resource allocation in a NOMA cognitive radio network with a practical non-linear energy harvesting model[J]. IEEE Access, 2017(6): 12973-12982.
[28] PRATHIMA A, GURJAR D S, NGUYEN H H, et al. Performance analysis and optimization of bidirectional overlay cognitive radio networks with hybrid-SWIPT[J]. IEEE Transactions on Vehicular Technology, 2020, 69(11): 13467-13481.
[29] JU H, ZHANG R. Throughput maximization in wireless powered communication networks[J]. IEEE Transactions on Wireless Communications, 2014, 13(1): 418-428.
[30] WANG F, ZHANG X. Secure resource allocation for polarization-based non-linear energy harvesting over 5G cooperative CRNs[J]. IEEE Wireless Communications Letters, 2020(99): 1.
[31] CHI K K, CHEN Z B, ZHENG K C, et al. Energy provision minimization in wireless powered communication networks with network throughput demand: TDMA or NOMA?[J]. IEEE Transactions on Communications, 2019, 67(9): 6401-6414.
[32] WU Q Q, CHEN W, LI J. Wireless powered communications with initial energy: QoS guaranteed energy-efficient resource allocation[J]. IEEE Communications Letters, 2015, 19(12): 2278-2281.
[33] BOYD S P, VANDENBERGHE L. Convex optimization[M]. Cambridge: Cambridge University Press, 2004.
[34] MOKHTARZADEH H, TAHERPOUR A, TAHERPOUR A, et al. Throughput maximization in energy limited full-duplex cognitive radio networks[J]. IEEE Transactions on Communications, 2019, 67(8): 5287-5296.
[35] HE S B, CHEN J M, JIANG F C, et al. Energy provisioning in wireless rechargeable sensor networks[J]. IEEE Transactions on Mobile Computing, 2013, 12(10): 1931-1942.
[36] XIAO H, JIANG H, SHI F R, et al. Energy-efficient resource allocation in radio-frequency-powered cognitive radio network for connected vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(8): 5426-5436.
[37] LI X Q, PAN C H, ZHANG C Y, et al. Data rate maximization in UAV-assisted C-RAN[J]. IEEE Wireless Communications Letters, 2020, 9(12): 2163-2167.
[38] XIAO H, JIANG H, DENG L P, et al. Outage energy efficiency maximization for UAV-assisted energy harvesting cognitive radio networks[J]. IEEE Sensors Journal, 2022, 22(7): 7094-7105.
Secondary throughput maximization scheme for non-linear energy harvesting cognitive radio networks
GE Haijiang1, JIA Ning1, CHI Kaikai2, CHEN Yunzhi1
1. College of Information Engineering, Hangzhou Vocational & Technical College, Hangzhou 310018, China 2. School of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China
Aiming at a cognitive radio network (CRN) consisting of a pair of primary users andpairs of secondary users, the secondary throughput maximization for CRN based on the non-linear energy harvesting model was studied. Specifically, in the case of considering secondary transmitter (ST) circuit power, the secondary throughput maximization (STM) problem with primary users’ throughput demands was first modeled as a non-linear optimization problem and then transformed into a convex optimization problem. Finally, a low-complexity algorithm combining the golden section and dichotomy was proposed. By applying this low-complexity algorithm, the optimal time allocation of the primary transmitter (PT)’s energy transmission and secondary users’ information transmission, and the optimal transmission power of PT were obtained. In addition, for the case of neglecting the ST circuit power, the convex property of the STM problem was first proved, and then a more efficient algorithm was designed to solve it. The simulation results show that compared with the equal time allocation method and the link gain priority method, the proposed design algorithm significantly improves the throughput of secondary users.
cognitive radio network, non-linear energy harvesting, secondary throughput maximization, low-complexity, convex optimization
TN929.5
A
10.11959/j.issn.1000–0801.2023033

葛海江(1980-),男,博士,杭州职业技术学院信息工程学院教授,主要研究方向为认知无线电网络。
贾宁(1981-),女,杭州职业技术学院信息工程学院副教授,主要研究方向为物联网应用。

池凯凯(1980-),男,博士,浙江工业大学计算机科学与技术学院教授、博士生导师,主要研究方向为无线电网络。
陈云志(1971-),男,博士,杭州职业技术学院信息工程学院教授,主要研究方向为物联网应用。
The National Natural Science Foundation of China (No.61872322), Zhejiang Provincial Basic Public Welfare Research Project of China (No.LGG18F020005)
2022-11-24;
2023-02-12
贾宁,492035425@qq.com
国家自然科学基金资助项目(No.61872322);浙江省基础公益研究计划项目(No.LGG18F020005)

