考虑个体恐慌与人群混乱的社会小群体疏散模型

陈晓薇，王 坚

（同济大学 电子与信息工程学院，上海 201804）

人群中往往存在由社会关系维系的小群体，如亲人、朋友等。与单独个体相比，社会小群体存在独特的疏散行为特点，如保持一起移动、分离后重新汇合以及选择相同的出口［1］。早期人群疏散模型将所有行人视为独立移动的个体，随着研究的深入，越来越多的学者关注到疏散人群中社会小群体的存在［2］。

人群疏散研究分可为2 个主要方向，真人试验与建模仿真。真人试验通常令参与者按一定的规则进行疏散演习，分析行人移动轨迹、疏散时间等数据。大多数真人疏散试验中，社会小群体被要求始终保持一起移动［3-4］。社会小群体与疏散时间的关系尚未形成一致性结论。有些研究认为社会小群体会延长疏散时间［5］，有些研究则表明疏散时间与小群体人数呈负相关［6］或双向关系［7］。然而在疏散演习时行人难以完全复现应急恐慌心理，实验结果的可复制性仍有待完善［8］。

人群疏散模型［9］实施更便捷、成本更低，通过定义行为交互规则［1］或群体吸引力［10］能够模拟社会小群体聚集行为，但小群体内部行为交互即走散后相互搜寻行为被普遍忽略了。搜寻行为导致的逆行迂回无疑会对人群疏散效率、混乱程度及恐慌水平造成影响。人群混乱作为疏散的关键影响因素，现有疏散模型却鲜少考虑其对个体疏散行为的影响。随着熵理论在人群运动状态检测［11］、异质性测量［12］和运动不稳定性检测［13］等问题中的广泛应用，熵也被引入到人群疏散模型中，通过个体速度概率分布的熵值来量化人群混乱状态［14-15］，但同时也有研究将其用于恐慌情绪的定量表征，造成人群混乱与恐慌情绪的概念混淆。更为常见的恐慌量化方法则是通过考虑个体到出口或危险源的距离、周围人群状态［16］以及情绪传播［17］等构建恐慌模型。

目前尚无人群疏散模型同时考虑小群体搜寻行为、人群混乱和恐慌情绪，三者间的关系仍有待探索。当社会小群体规模较大时，因为空间结构大、视野限制、人群拥挤等原因更易走散，行为模式也更加复杂。本文基于成对社会小群体疏散模型的研究［18］，提出了一个考虑个体恐慌与人群混乱的社会小群体疏散模型（The evacuation model for social groups considering individual panic and crowd chaos，EMSPC），模拟包含多人社会小群体的异质人群疏散过程。基于OCEAN性格模型［19］描述行人恐慌情绪，采用玻尔兹曼熵量化个体对周围人群混乱的感知，并将恐慌值和熵值引入个体速度更新，分析多人社会小群体对人群恐慌情绪、混乱程度及疏散效率的影响。

1 模型介绍

基于Agent 的仿真模型能够通过微观个体行为规则涌现出宏观群体行为，揭示群体自组织现象以及动态演化。EMSPC 模型采用基于Agent 的仿真框架，将疏散个体抽象为具有不同属性的两类Agent，即独立个体和社会小群体。所有个体视野范围为半径5m、夹角200°的扇形区域，感知范围为半径2m的圆形区域，速度增量ΔVi由自身行为规则决定。疏散场景被离散化为1m×1m的网格。

1.1 独立个体的行为规则

独立个体在疏散时会优先移向出口，并表现出与距离过近的行人、障碍物相排斥，同时出于从众心理向周围人群聚集。依据这些行为动机，独立个体i的速度增量ΔVi由出口速度Vexit、聚集速度Vcohere和避障速度Vavoid按优先级系数{ωL，ωM，ωS|ωL>ωM>ωS≥0}构成：

设个体i视野内距离出口最近的网格为Pexit−goal，可见行人共k个，与i距离小于2m且距离最近的行人位置为Pobstacle，则个体i的出口速度、聚集速度和避障速度分别为

1.2 社会小群体搜寻策略

为社会小群体设计理性策略A 和非理性策略B。设人群中小群体的人数均为n，个体i为小群体成员，t时刻可见同伴共m个（m>0），分别为同伴j的速度和位置，则i与可见同伴的同行速度和汇合速度分别为

策略A：当所有同伴均不可见，个体i放弃逃逸，根据是否存在可见行人，选定搜寻目标PAgoal为可见行人或最远网格；当所有同伴均可见，i不搜寻同伴，向出口逃逸的同时向可见同伴汇合并保持同行；当部分同伴可见，i优先与可见同伴汇合，同时搜寻不可见同伴并逃向出口。

策略B：当所有同伴均不可见，个体i放弃逃逸，随机选择周围5m内的任一网格作为搜寻目标PBgoal；当所有同伴均可见，i不搜寻同伴，行为规则与独立个体相同；当部分同伴可见，i放弃逃逸，并根据可见同伴的数量决定是优先搜寻同伴还是优先与可见同伴保持同行。

个体i的移动速度根据恐慌值Ei(t)和熵值Si(t)进行更新

考虑个体恐慌和人群混乱的社会小群体疏散模型的流程如图1所示。

图1 EMSPC模型算法流程Fig.1 Flowchart of EMSPC algorithm

1.3 个体恐慌情绪模型

为量化个体恐慌情绪，改进情绪传染模型［20］将其引入EMSPC模型。个体恐慌情绪Ei(t)由累积恐慌(t)、传染恐慌(t)和环境引发的恐慌(t)构成。

式中：(t)为个体i前一时刻恐慌水平经衰减后的值，衰减比例η∈(0，1]。

EMSPC 模型定义恐慌传播取决于个体的表达阈值和被感染阈值。两者由OCEAN 人格模型［19］性格变量ϕO、ϕ、ϕE、ϕA、ϕN即个体的经验开放性、尽责性、外向性、随和性和情绪稳定性表示。所有个体的5个性格变量均为［−1，1］内的随机值。情绪阈值计算为

当个体恐慌大于表达阈值则传播恐慌。若个体i感知范围内行人传播的恐慌值总和大于其被感染阈值，i会受到恐慌传染。设有效传染时限为10个时间步长，Ej(t′)和d(t′)分别为t′时刻可见行人j的恐慌情绪与传染系数，t时刻个体i被传染的恐慌值(t)为

(t)为个体到出口的距离dexit以及小群体走失人数Nlost导致的恐慌［16］。

式中：α=0.05 表示出口距离和走失同伴数对个体恐慌的影响系数。独立个体的恐慌程度仅受出口距离的影响，即距离出口越远越恐慌；对于社会小群体，除了出口距离外，不可见同伴越多，恐慌情绪越严重。

1.4 人群熵

引入玻尔兹曼熵来量化个体对可见行人混乱的感知。设t时刻个体i视野内共有M个可见行人，将个体速度方向和大小取值范围4 等分，构成4×4 的速度分布空间。将各分布区间内的人数按从多到少记为

可知，熵值由速度微观状态数W决定。为确保将熵值用于速度更新的合理性，将计算系数玻尔兹曼常量调整为0.013 8。

2 仿真实验

采用Netlogo 仿真软件模拟人群疏散过程。设疏散总人数为200，疏散前随机分布在41m×41m的单出口房间，出口宽度为1m。模型参数默认值如表1所示。仿真表明，EMSPC 模型能够有效复现人群疏散的经典现象“出口拱型拥堵”。

表1 EMSPC模型参数说明Tab.1 Parameter description of EMSPC model

2.1 社会小群体的搜寻行为

为分析社会小群体搜寻行为的特点，分别模拟了包含10组3人或6人社会小群体、总人数为200的人群疏散过程。

2.1.1 采用策略A的人群疏散过程

如图2，t=15s 时有3 组3 人小群体发生成员走散，其中一组在t=22s 时汇合，剩下2 组仍继续搜寻。在疏散中后期，个别小群体成员因为寻找同伴而放弃逃逸，离开出口附近返回房间搜寻，且随机搜寻持续时间较长。

图2 3人小群体采用策略A的疏散过程Fig.2 Evacuation process of small group of three people adopting Strategy A

如图3，t=5s 时部分6 人小群体分裂成更小的群体，符合实际疏散现象［22］。t=21s时，所有个体聚集到出口附近，仅有1 个小群体成员存在不可见同伴。在疏散中后期，搜寻行为主要发生在出口拱型拥堵外侧，虽仍存在返回房间的搜寻行为，但持续时间较短。此外，小群体成员在出口排成流线型，复现了真实疏散试验观察到的现象［23］。

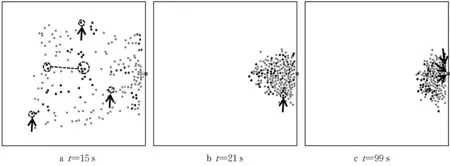
图3 6人小群体采用策略A的疏散过程Fig.3 Evacuation process of small group of six people adopting Strategy A

2.1.2 采用策略B的人群疏散过程

对比图4和图2，当t=15s时，相同初始分布的3人小群体采用策略B时走散人数更多。这表明若小群体缺乏理性判断，走散的概率更大。在疏散中期存在小群体成员结伴搜寻的现象，且结伴搜寻的行人移动速度比独自搜寻同伴的个体慢。疏散后期独立个体均已逃出后，仍有小群体成员不放弃寻找同伴，导致人群疏散时间变长。

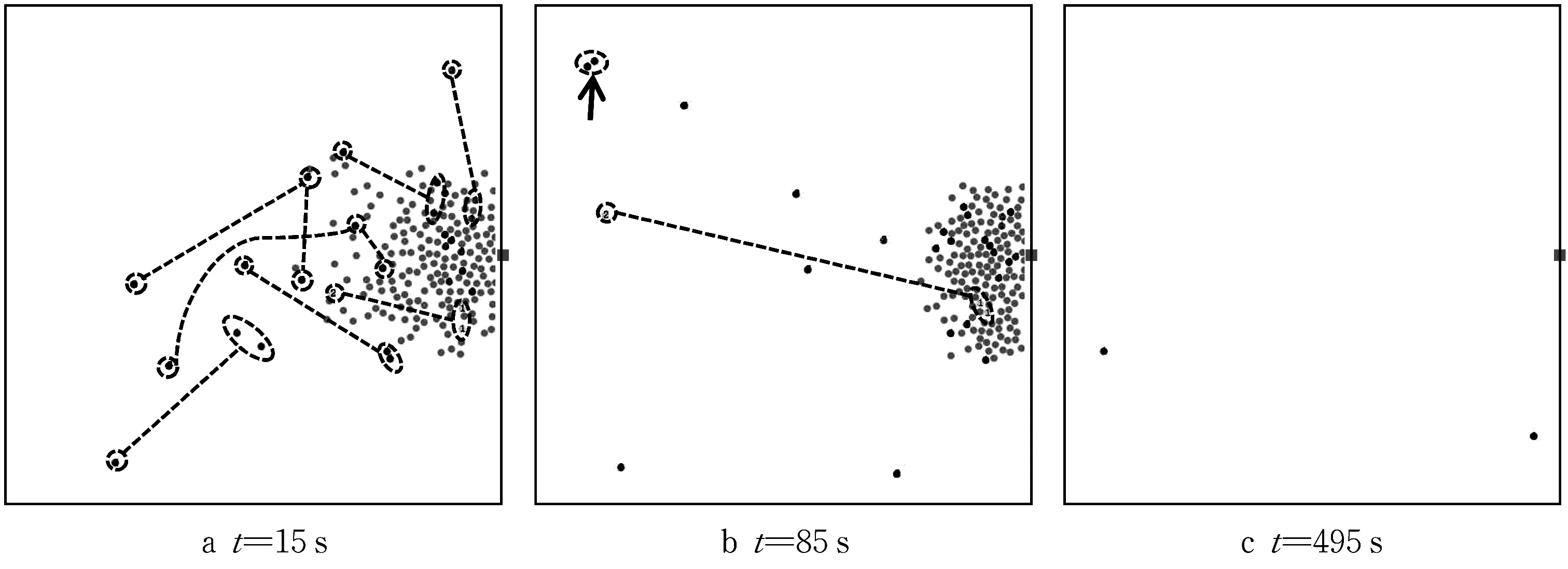
图4 3人小群体采用策略B的疏散过程Fig.4 Evacuation process of small group of three people adopting Strategy B

由图5可知，6人非理性小群体在疏散初期会分裂为2 个或者更多的更小的群体，且结伴搜寻。疏散后期放弃逃逸返回房间搜寻的人数比3人小群体和采用策略A时更多。这是因为小群体人数多且缺乏理性判断，因此走散概率更大，而随着疏散后期出口拥堵程度降低，减少了随机搜寻的阻碍，导致搜寻行为的不确定性增加。

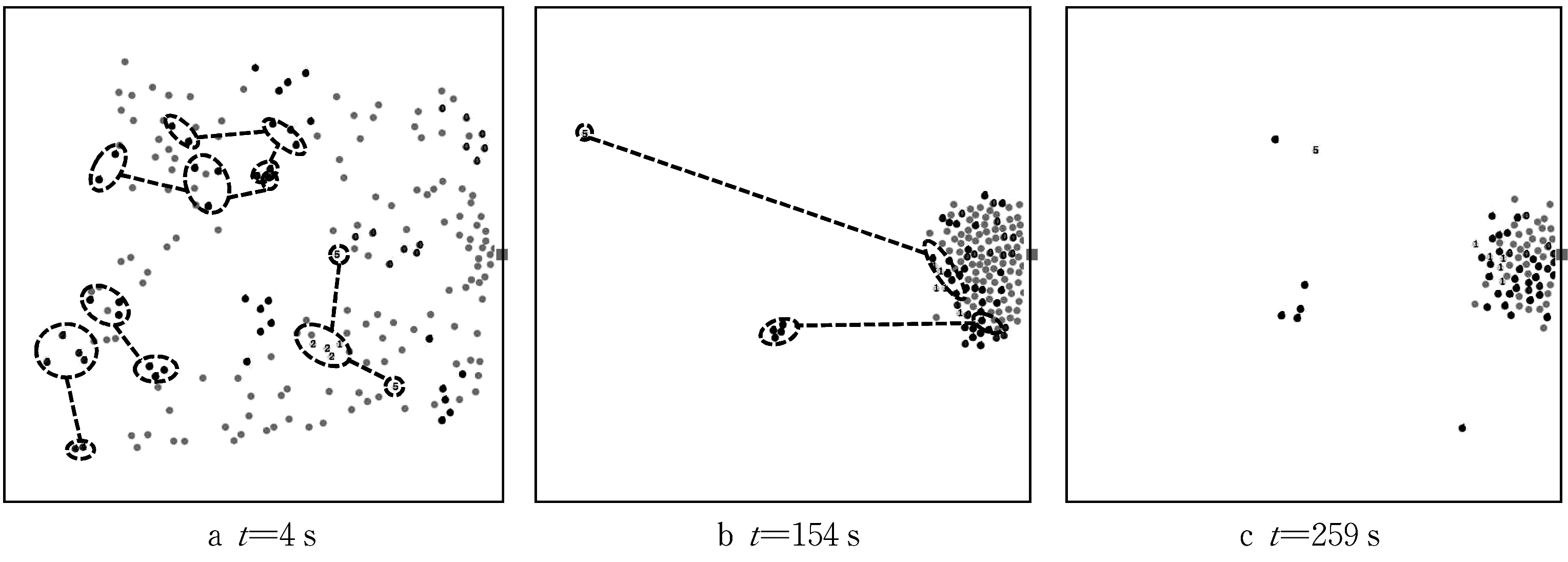
图5 6人小群体采用策略B的疏散过程Fig.5 Evacuation process of small group of six people adoptimg Strategy B

2.2 恐慌情绪的实时分布

基于疏散场景离散网格内个体恐慌的平均值将人群恐慌水平可视化，网格颜色越深，表明该网格内行人的恐慌水平越高。

由图6可知，采用策略A时，在疏散初期人群恐慌水平与出口距离正相关。在疏散中期最恐慌的网格位于出口拱型拥堵的边缘。疏散后期恐慌最严重的区域为搜寻同伴的个体所在网格或出口拱型的边缘。对比图6 中含不同人数小群体的疏散过程可知，采用策略A 时小群体人数对恐慌分布的影响不大。

图6 采用策略A疏散时的恐慌情绪分布Fig.6 Panic distribution of evacuation adopting Strategy A

如图7 所示，采用策略B 时，在疏散初期行人恐慌水平与出口距离正相关，而在疏散中后期，小群体人数对恐慌分布影响较大。在疏散中期，6人小群体搜寻同伴的行为引发局部恐慌升高，在疏散后期出口附近人群恐慌水平也比3人小群体更严重。由此可知，对于非理性社会小群体，增加小群体人数将导致疏散中后期恐慌分布的变化与加剧。

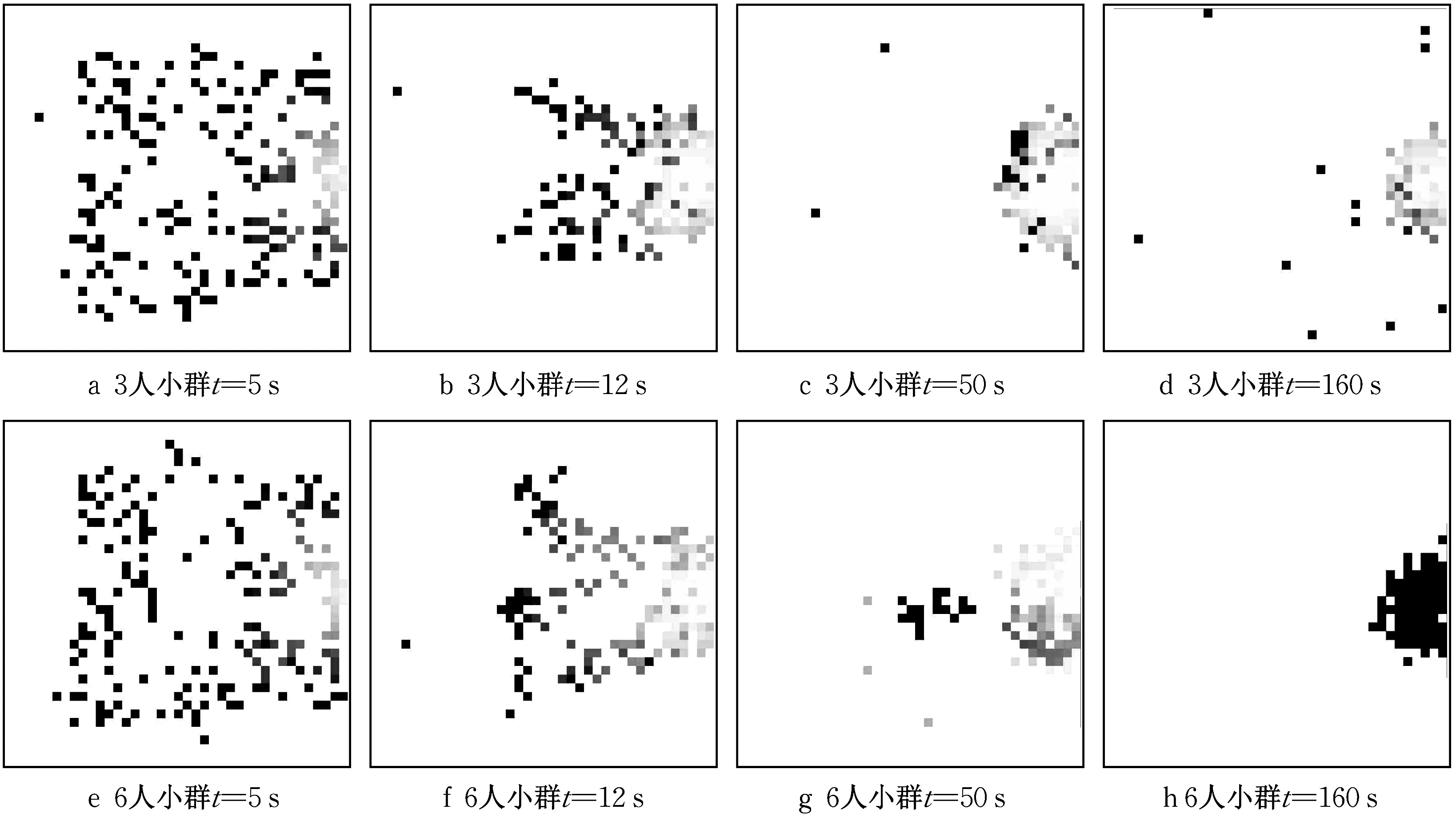
图7 采用策略B疏散时的恐慌情绪分布（t=5s，12s，50s，160s）Fig.7 Panic distribution of evacuation adopting Strategy B

2.3 社会小群体对人群疏散过程的影响

取50 次随机初始条件下的平均疏散仿真结果来分析社会小群体数量与疏散时间、恐慌情绪及人群混乱间的关系。

2.3.1 疏散时间与小群体数量的关系

如图8，当小群体组数固定时，疏散时间随小群体人数增加没有明显单调变化趋势，疏散时间的波动反映了不确定性，这是由搜寻行为导致的。非理性小群体搜寻目标更随机，增加了人群疏散时间的不确定性。当小群体人数固定，随组数增大，采用策略B时人群疏散时间的增幅远超策略A。这是因为采用策略A 时个体理性选择搜寻目标，且只要有同伴可见就不放弃逃逸，因此折返或持续搜寻的现象较少，小群体对疏散时间的影响相对较小。

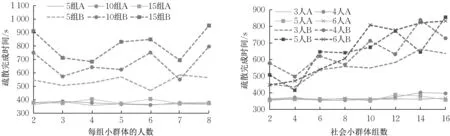
图8 疏散时间与社会小群体数量的关系Fig.8 Evacuation time versus number of small social groups

2.3.2 人群混乱与小群体数量的关系

如图9，人群历史最大熵随小群体的人数或组数增加而增大。采用策略B的人群其历史最大熵的增幅比采用策略A 的人群更大，说明非理性策略会使小群体数量对疏散人群混乱程度的负面影响更显著。对于采用策略A 的人群，6 人小群体在组数小于10时比5人小群体更有序，随着组数增加，熵值超过5 人小群体和非理性3 人小群体。这说明理性大规模小群体对人群混乱程度存在双重影响。

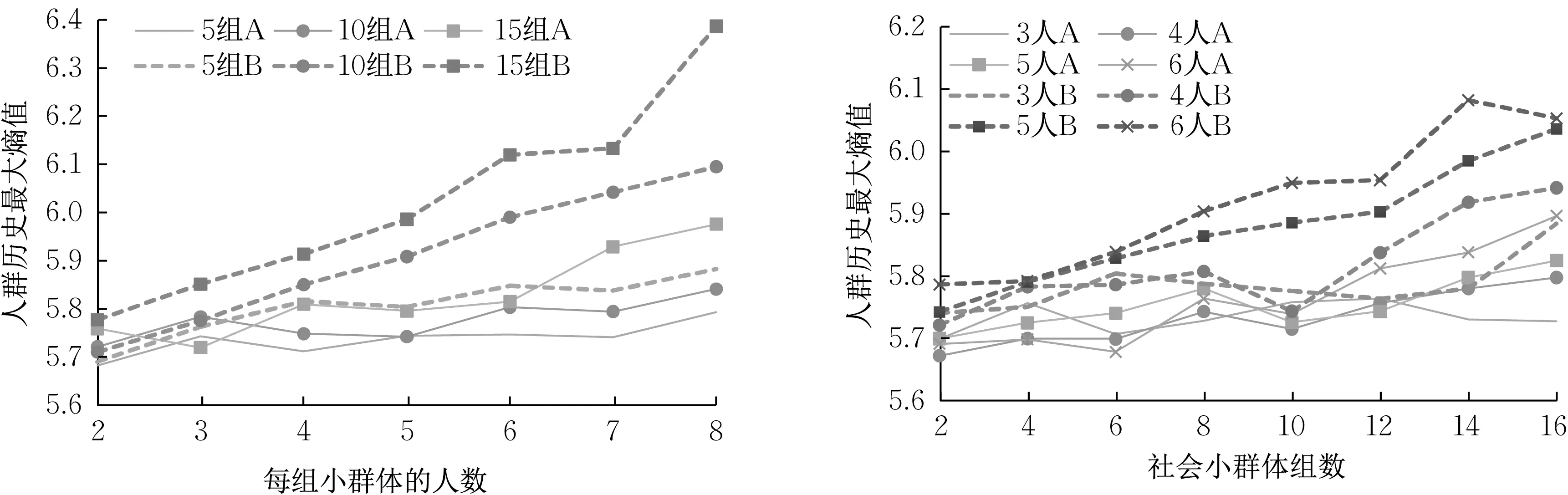
图9 人群混乱程度与社会小群体数量的关系Fig.9 Degree of population disorder versus number of small social groups

2.3.3 恐慌情绪与小群体数量的关系

如图10，当小群体组数固定，瞬时恐慌峰值为3或4人小群体。策略A的瞬时恐慌没有明显的单调变化趋势。当小群体人数固定，瞬时最大恐慌随着小群体组数增加。采用策略A时的恐慌值整体低于策略B，表明小群人能否理性搜寻对恐慌程度存在较大影响。当小群体无法理性搜寻同伴时，小群体组数对个体恐慌情绪影响更大。

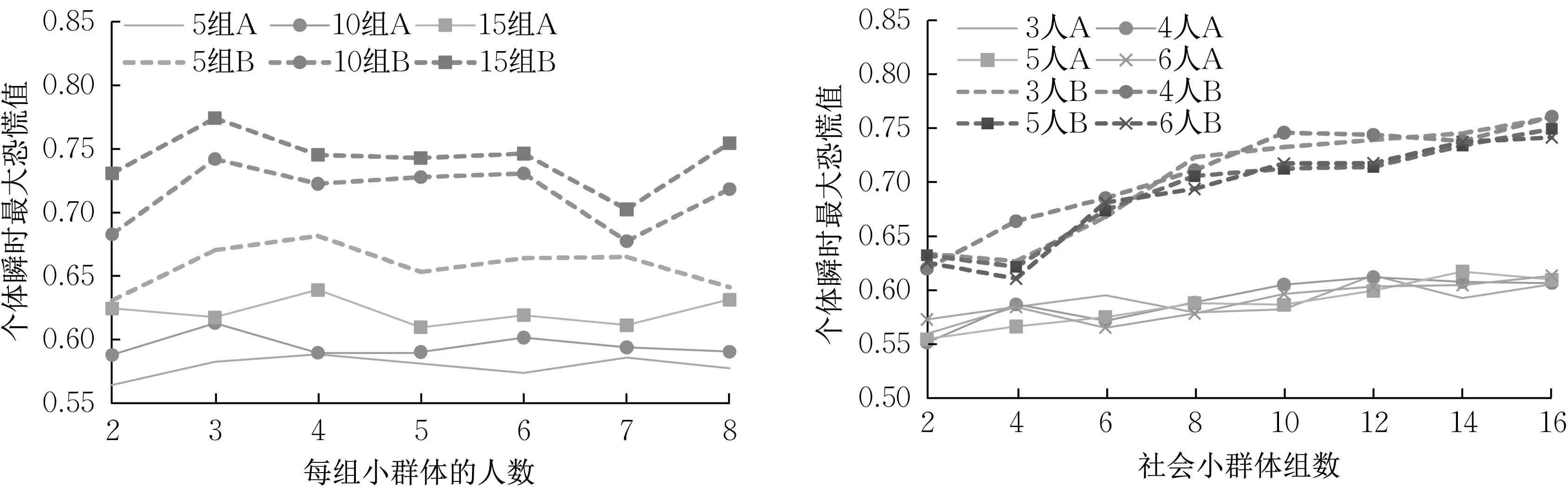
图10 社会小群体与行人恐慌情绪的关系Fig.10 Small social groups versus pedestrian panic mood

3 结语

提出了一个考虑个体恐慌与人群混乱的社会小群体疏散模型，可以模拟含多人社会小群体和单独个体的混合人群在恐慌及混乱影响下的疏散过程。实验表明，多人社会小群体特别是儿童、老人等非理性小群体的搜寻同伴行为多发生于拱形拥堵外侧，对人群疏散效率、混乱及恐慌程度存在负面影响。EMSPC 模型可作为疏散人群恐慌与混乱状态的分析工具，加深对多人社会小群体疏散行为的理解，为进一步探索社会小群体复杂行为对疏散过程的影响提供科学参考依据。

作者贡献声明：

陈晓薇：算法设计与实验分析、论文撰写。

王 坚：研究指导、经费支持、论文修改。