基于GeoGebra软件对“磁聚焦”模型的可视化研究

蔡丁澄，宋善炎

湖南师范大学物理与电子科学学院，长沙 410081

“磁聚焦”模型是高中物理教学中一个重要的二级结论，也是物理高考的热点问题。在日常教学中发现，很多学生难以建构不同条件下带电粒子在磁场中运动的模型。为了让物理模型更加直观、形象，让物理教学更加生动、全面，教师可以借助动态数学软件GeoGebra提供的可视化技术进行辅助教学［1］，帮助学生建构抽象模型。

1 GeoGebra软件

GeoGebra是一款集几何、代数和微积分为一体的免费数学教学软件，它可以从GeoGebra官方网站下载，可以脱机使用。GeoGebra具有几何画板的所有功能、Flash的部分功能以及Excel的常用功能。使用者不需要编程也能进行数值模拟，相比于其他教学软件，GeoGebra更加容易上手使用。抽象化是学生对物理知识的认知常态，利用GeoGebra软件将抽象的物理知识直观地展示出来，使物理知识图像化、具体化，从而有效降低学生的思维难度。因此，GeoGebra软件是一款非常适合物理可视化教学的辅助工具。

2 “磁聚焦”模型的可视化教学

2.1 “磁聚焦”模型

电荷量相等的带电粒子以大小相等的速度平行射入匀强圆形磁场，当带电粒子运动的轨迹圆半径r与磁场圆半径R相等时，所有的带电粒子将汇聚在磁场圆的最低点上，此现象称为“磁聚焦”，如图1（a）所示。反之，同种带电粒子束以相同的速度射入磁场边界的最低点且R=r时，带电粒子束经过磁场区域的偏转后沿相同方向平行射出，这种现象称为“磁发散”，如图1（b）所示［2］。

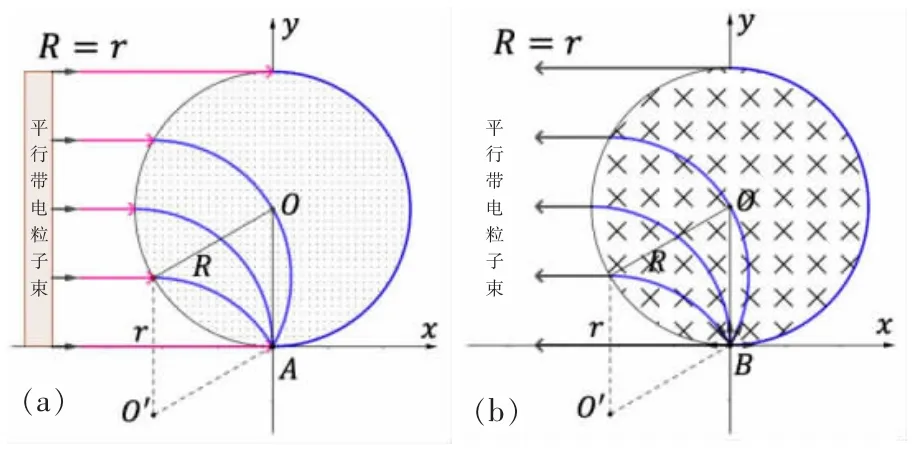
图1 “磁聚焦”和“磁发散”

2.2 原题呈现

2021年湖南省高考物理第13题是一道典型的“磁聚焦”模型的题目，难度较大。以该题的教学为例，介绍如何利用GeoGebra软件进行“磁聚焦”模型的可视化教学。

例题（2021年湖南省高考物理第13题）带电粒子流的磁聚焦和磁控束是薄膜材料制备的关键技术之一，带电粒子流（每个粒子的质量为m、电荷量为+q）以初速度v垂直进入磁场，不计重力及带电粒子之间的相互作用。对处在xOy平面内的粒子，求解以下问题。

（1）如图2（a），宽度为2r1的带电粒子流沿x轴正方向射入圆心为A（0，r1）、半径为r1的圆形匀强磁场中，若带电粒子流经过磁场后都汇聚到坐标原点O，求该磁场磁感应强度B1的大小。

（2）如图2（a），虚线框为边长等于2r2的正方形，其几何中心位于C（0，-r2）。在虚线框内设计一个区域面积最小的匀强磁场，使汇聚到O点的带电粒子流经过该区域后宽度变为2r2，并沿x轴正方向射出。求该磁场磁感应强度B2的大小和方向，以及该磁场区域的面积（无需写出面积最小的证明过程）。

（3）如图2（b），虚线框Ⅰ和Ⅱ均为边长等于r3的正方形，虚线框Ⅲ和Ⅳ均为边长等于r4的正方形。在Ⅰ、Ⅱ、Ⅲ和Ⅳ中分别设计一个区域面积最小的匀强磁场，使宽度为2r3的带电粒子流沿x轴正方向射入Ⅰ和Ⅱ后汇聚到坐标原点O，再经过Ⅲ和Ⅳ后宽度变为2r4，并沿x轴正方向射出，从而实现带电粒子流的同轴控束。求Ⅰ和Ⅲ中磁场磁感应强度的大小，以及Ⅱ和Ⅳ中匀强磁场区域的面积（无需写出面积最小的证明过程）。

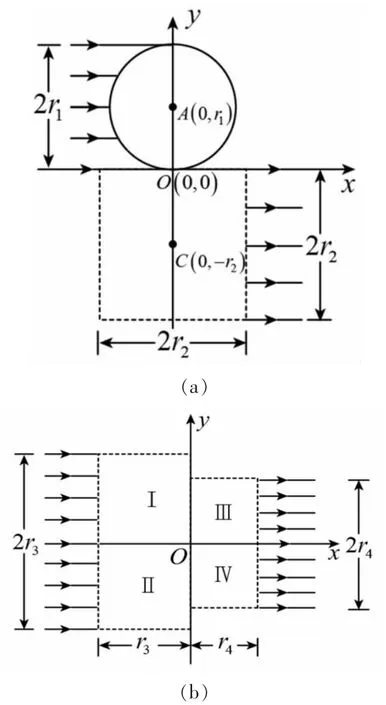
图2 2021年湖南省高考物理第13题原图

2.3 具体示例

此考题以磁聚焦和磁控束是薄膜材料制备的关键技术为背景，考查的是磁场中的轨道半径恰好等于磁场圆的半径时的磁聚焦的问题、最小圆域磁聚焦问题以及平面磁场蝶形磁聚焦问题［3］。问题（1）中，带电粒子沿x轴正方向射入圆形磁场，要求带电粒子经过圆形磁场汇聚到O点，满足磁聚焦的条件。只有带电粒子的轨迹圆半径r等于磁场圆半径r1时，带电粒子才能在O点汇聚。由粒子在磁场中运动时洛伦兹力提供向心力，可列出关系式：

下面，利用GeoGebra软件绘制“磁聚焦”模型来求解问题（1）。

第一步，建立题干的背景模型。设置r，r1，α，v的滑动条，α是入射点P和O（0，0）的连线与x轴正方向的夹角。再使用菜单栏的作图工具在绘图区绘制出圆心位于A（0，r1）、半径为r1的圆形磁场区域，磁感线方向垂直纸面向外。描点P（r1sin2α，r1-r1cos2α），Q（r1sin2α-v，r1-r1cos2α），P 为入射点。向量为入射速度，如图3（a）所示。改变α，模拟带电粒子从y轴左侧的磁场圆边界平行射入磁场，如图3（b）所示。

第二步，绘制带电粒子在磁场区域运动轨迹，如图3（c）所示。描点O'（r1sin2α，r1-r1cos2α-r），作以O'为圆心、半径为r的带电粒子轨迹圆，点C为轨迹圆与磁场圆的交点（由于O'和C点是动点，未在图中标记）。多次改变r和r1的大小，发现只有当r=r1时，点C与点O重合，带电粒子才能从O点射出。

第三步，模拟“磁聚焦”模型。改变滑动条α，使带电粒子流在磁场圆O点汇聚并射出，如图3（d）所示。

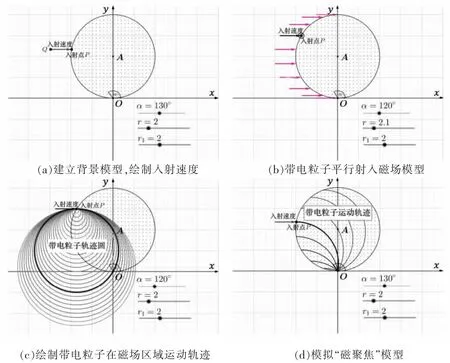
图3 利用GeoGebra软件绘制问题（1）中的模型

问题（2）要求粒子从O点进入下方虚线区域后飞出磁场且速度方向与x轴平行，这样的现象为磁发散过程，即粒子在下方圆形磁场运动的轨迹半径r等于磁场半径r2。同问题（1），可得B2=，粒子平行于x轴正方向飞出。根据左手定则，磁场方向为垂直纸面向里。

如果带电粒子做匀速圆周运动的轨迹半径r、磁感应强度B2、速度v、质量m、电荷量+q的大小已知，那么能实现“磁聚焦”的匀强磁场最小面积为多大呢？可以通过数学方法，设入射速度与x轴正方向的夹角为θ（0≤θ≤π），带电粒子轨迹圆圆心为O'（i，j），射出磁场的位置点为Q（x，y）。则可列出关系式：

x=rsinθ；y=rcosθ-r；i=rsinθ；j=rcosθ

解方程，得：

i2+j2=r2；x2+（y+r）2=r2（0≤x≤r，-r≤y≤0）

可知，带电粒子轨迹圆的圆心位于以（0，0）为圆心、半径为r的圆周上。射出点位于以（0，-r）为圆心、r为半径、y轴右侧的圆周上。因此，利用微元思想求解，带电粒子在磁场中运动的速度方向变化角从θ变化到θ+dθ时，对应的运动轨迹包围的面积为dS，得：

以上是用数学方法解答“磁聚焦”的匀强磁场最小面积的教学过程，但学生理解起来有一定难度。而利用GeoGebra软件演示粒子的运动过程，可以展示出学生不易想象的物理图景，引导学生的思考过程，化“难”为“易”，学生的解题思路将会豁然开朗。

第一步，建立题干的背景模型。设置r2的滑动条。再使用菜单栏的作图工具在绘图区中绘制出几何中心位于C（0，-r2）、边长为2r2的正方形虚线框以及带电粒子的入射点O（0，0），如图4（a）所示。

第二步，绘制入射速度。设置v，θ的滑动条，v是速度的大小，θ是速度方向与x轴正方向的夹角。描点P（vcosθ，-vsinθ），使用向量工具，绘制向量为入射速度，如图4（b）所示。

第三步，绘制射出速度。设置x，y的滑动条。描点Q'（r2sinθ，r2cosθ-r2），R（r2sinθ+v，r2cosθ-r2），使用向量工具，绘制向量为射出速度，如图4（c）所示。

第四步，模拟射出点变化轨迹。通过改变θ滑动条，可以清楚地演示带电粒子射出点的轨迹变化，如图4（d）所示。

第五步，绘制带电粒子在磁场区域的运动轨迹。描点O'（r2sinθ，r2cosθ），O'为带电粒子轨迹圆圆心。以O'为圆心、半径为r2作圆。利用圆弧工具，绘制带电粒子在磁场区域运动轨迹，如图4（e）所示。

第六步，模拟带电粒子在磁场区域的变化轨迹。通过改变θ滑动条，可以清楚地演示带电粒子在磁场区域的运动轨迹是以C（0，-r2）为圆心、半径为r2的圆，如图4（f）所示。这也是实现“磁聚焦”的最小匀强磁场区域，其面积大小为

图4 利用GeoGebra软件绘制问题(2)中的模型

通过代数及指令输入，可以精确绘制模型，使用滑动条实现图形的动态变化，从而演示可实现“磁聚焦”的最小匀强磁场区域。

问题（3）与问题（2）的求解方法类似。根据左手定则，可以判断出Ⅰ和Ⅲ区域的磁场方向。由洛伦兹力提供向心力可以列出等式，从而求得Ⅰ区域和Ⅲ区域的磁感应强度大小。分析可知，一部分带电粒子从Ⅰ区域入射，经过磁场区域的偏转后在O点汇聚，再从O点射入到Ⅳ区域进行偏转运动，最后平行于x轴正半轴射出。另一部分带电粒子是从Ⅱ区域入射经过磁场区域的偏转后在O点汇聚，再射入到Ⅲ区域进行偏转运动后平行于x轴正半轴射出。

下面以Ⅰ和Ⅳ区域为例，利用GeoGebra软件演示带电粒子的运动轨迹，并模拟出Ⅰ和Ⅳ区域的最小磁场区域。与问题（2）的绘制步骤相似。首先，选择合适的工具绘制出四个区域，再设置β滑动条，β为粒子射出Ⅰ区域时速度与x轴正半轴的夹角。然后，根据入射点与射出点（汇聚点）的几何关系，绘制出入射点位置和入射速度。再根据入射点与轨迹圆圆心的几何关系，找出轨迹圆的圆心O'，作出轨迹圆。最后，利用圆弧工具，作出带电粒子在磁场区域的运动轨迹。改变β滑动条，带电粒子束在磁场区域运动轨迹所覆盖的区域就是最小的磁场面积（图5），其值为同理，Ⅱ和Ⅳ区域的最小磁场区域像两片“绿叶”［4］，其面积分别为

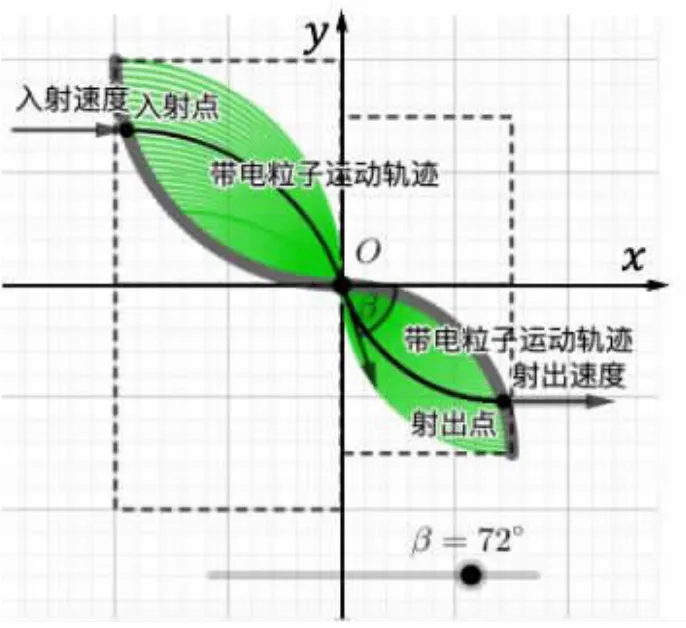
图5 两片“绿叶”：最小磁场区域

3 结语

借助GeoGebra软件的多功能几何绘图工具进行可视化教学，可以将较难的抽象思维模型直观地呈现在学生面前，让学生在学习过程中充分理解“磁聚焦”这个二级结论。这种融合信息技术的物理教学过程，不仅能有效提高学生的学习效率，而且能有效培养学生的模型建构能力，提升学生的学科核心素养，值得应用和推广。