论数形结合思想在“双减”之下数学教学中的应用

江苏省江阴市璜土实验小学 金雪强

数形结合思想是一种重要的教学思想方法，教学中教师要重视数形结合思想的运用。本文就数形结合思想在“双减”之下数学教学中的应用进行了探究。

一、数形结合思想的教学价值

数形结合思想的实质就是数学学习过程中的两大组成部分——“数”与“形”二者之间的相互转化、表达，以及其在实际问题中的相关运用。而对于“数”与“形”二者之间的相互转换、表达，以及其在实际运用中的相互解决问题，便是教师在数学教学过程中培养学生数形结合思想、帮助学生建立数学逻辑分析能力的一种重要方式。

就“数”与“形”之间的“相互转化”而言，我们可以通过观察“形”来加深对“数”的理解，同时，也可以通过对“数”的计算来加深对“形”更加直观的理解。

比如，在教学“负数的认识”相关的内容时，教师可以把温度计带到课堂上作为教具，让学生通过观察温度计零上刻度和零下刻度来理解负数的概念。

就“数”与“形”之间 “相互表达”而言，教师可以用“形”来表示“数”，并以此来使学生真正理解教学过程中的数量关系。同样，也可以用“数”来表示，从而将“形”更加准确地表现出来。这样一来，便加深了“数”与“形”之间的联系，使学生对数量关系的分析能力及逻辑思维能力都得到了提升。

就“数”与“形”之间“相互解决问题”而言，这一内容是在“数”与“形”之间相互转化与相互表达的基础上来完成的。比如，在教学“时间的认识”这一内容时，教师在教学过程中则应该利用与学生息息相关且便于学生理解的事物，例如我们每个人都经历的春、夏、秋、冬这四个季节，这些便可以使学生更加直观地去感受时间，而这四个季节便是时间所存在的一种“形”，其中包含的时间便是“数”。但是，在小学数学教学过程中，教师往往通过钟表中的指针所指以及钟表面上的时间刻度来对学生展开教学，并以此来使学生对时间有更深层次的认识。就这一教学过程而言，教师实则是忽视了“时间”这一事物中“数”与“形”之间的关系，忽略了“数形结合”思想在教学中的价值。新课标明确指出：“几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。”纵观这部分内容，其中便包含了“以形助数” “以形解数”这些内容，使“数”与“形”之间的表达与转换更加直观、形象，使学生在学习过程中的逻辑思维能力与运算能力均得到加强。

二、数形结合思想在教学中的实际应用

（一） “数形结合” 让教学表达更加直观

数学是一门以数量关系与实际问题相结合为基础的学科，其中，大量的数学计算过程使数学学习变得较为枯燥乏味。应用题是学生在小学数学中接触较多的一部分内容，但是很多学生对于应用题的题干分析不透彻，无法真正理解题意，遇到条件较为复杂的情况，则无法解决相关问题。而“数形结合”这一教学思想就是将抽象的问题直观化，即通过将题干转化成图形，从而使学生通过图形的结构特点来发现其中所包含的数量关系。这样一来，复杂抽象的数量关系便可以通过图形更加直观地显现出来，从而帮助学生理解题意，找到解决实际问题的方法。同时，教师教会学生以数化形、以形化数，并用这种思维来解决相关的数学问题，这让学生在数学学习时不再感到枯燥，从而提升主动学习数学的积极性，数学课堂教学质量由此得以大幅度提升。

例如：小明的家离学校1000米，小明每天必须在8点前到达学校。小明的速度是80米每分钟，在小明出发5分钟以后，小明的爸爸发现了小明没有带课本，以180米每分钟的速度出门追小明。

（1）小明的爸爸多久追上小明？

（2）追上小明时，距学校多远？

对于这一题目，教师应当引导学生对题目中的等量关系进行分析，而分析等量关系则需要运用到数形结合工具。在画出图后，等量关系变得一目了然，学生便可求出最终结果。

（二） “以数想形”帮助学生理解公式含义

在小学数学教学过程中，经常会出现关于公式的教学内容，倘若教师在进行教学时，只是片面地让学生去死记硬背公式，这节课的课堂教学便毫无意义。因为学生只是片面地记住了公式，却无法真正理解其中的含义，也无法对这些公式进行有效运用。即使教师在课堂教学中给出了考查某些公式时常出现的题干，但是一旦题干稍做变化，学生就会对相关题目无从下手，无法真正做到“举一反三”。 因此，教师在教授学生相关公式时，必须要让学生理解透彻，不能只是单一地让学生记忆公式。

例如在长方形周长公式的教学过程中，教师便可以通过图形来帮助学生充分理解该周长公式的含义。一般而言，长方形周长可以用三种方式求得：（1）长+宽+长+宽；（2）长×2+宽×2；（3）（长+宽）×2。对前两种计算方法，学生比较容易理解，这也是大多数学生经常用到的方法。一般而言，第三种长方形周长的计算方法较少被用到，根本原因在于学生对长方形公式理解不够深入。针对这种情况，教师可以借助“火柴”等教学辅助工具来进行讲解，为学生介绍第三种求解长方形周长的方法，使学生理解更加透彻。

（三）“数形结合” 发展学生立体空间思维

对数形结合的教学思想，教师可以将其中的理论部分与学生的实际生活有机地联系起来。 就小学生的认知规律而言，他们通常都是先直接感受到表象内容，其次才会对其形成的过程进行探究。而教师在教学过程中则要紧密结合学生的实际情况，让他们学会从不同的角度去对数学问题进行思考，留给学生足够的空间去想象，使学生的想象力、创造力等得以提升。

例如，在教学“图形与几何”时有这样一道题：“将边长为10厘米的正方形四个角各截去边长为2厘米的小正方形，那么剩下的图形的周长为多少呢？”

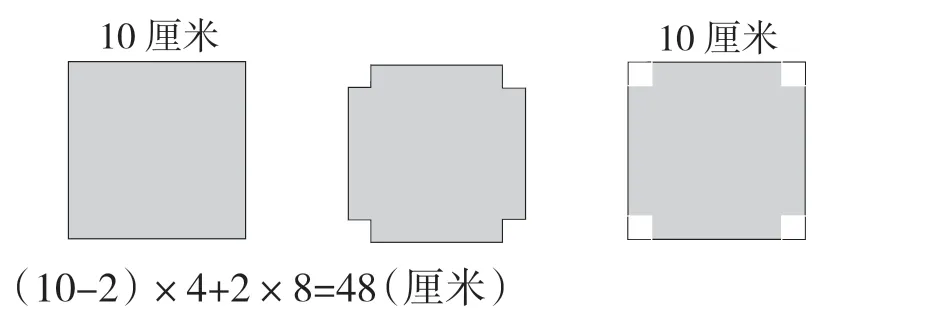
对这道题，教师可以用多媒体进行图形展示，通过动画的形式为学生分析题目，在此过程中让学生逐渐明白周长和原图周长之间的联系。

三、对学生数形结合思维的培养

（一）教师要挖掘教材中的数形结合思想

数学学习的过程，并不仅仅是要向学生灌输数学知识，更重要的是要让学生通过这个学习过程，对数学思想深刻理解、掌握并运用。数学思想潜藏在万千数学知识点中， “数形结合”的思想也同样不例外。比如数学学习中涉及的分数、因数、倍数等这些概念，教师通过教授学生运用数形结合思想便可以有效帮助他们理解这些概念。此外，在解决实际问题的过程中，数形结合思想也同样可以作为一种解题的策略加以运用。 这样一来，学生就可以在解决相关题型的过程中有效分析题目中所涉及的数量关系，同时教师也可以为学生直接揭示其中所蕴含的数量关系，使学生有更加清晰的理解，真正实现数学课堂教学的多元化。

（二）教师要以数学情境培养学生数形结合思想

枯燥乏味的数学教学会逐渐使学生失去学习的兴趣。针对这一教学问题，教师可以合理地设置有意思的、多元化的教学场景，把教授的数学知识和学生的现实生活进行联系结合，以此来激发学生对所学数学知识的兴趣，引导学生以看图、读图的方式，从图中发现、提出、分析、解决问题，让他们在这个过程中加深对数形结合方法的认识和理解，真正体会到数形

结合思想在实际运用中的重要作用，明白“数”与“形”之间的重要关联。

（三）教师要带领学生在探索中理解数形结合思想

新课程改革后，学生在课堂教学中应当占据主体地位，而不是像传统教学方法下的整堂课以教师为主体。同样，教师要想真正培养学生数形结合的思想和能力，就要让学生在丰富多彩的学习活动中去体验、去学习、去实践。而在这个过程中，教师应当充分激发学生的思维活力，让学生在自主学习的过程中提升发现、提出、解决问题的能力，带领学生在探索中理解数形结合思想。

（四）教师要以课后练习促进学生理解数形结合思想

教师对学生数形结合思想的培养是一个较为持久的过程，由于每个学生的基础不同，教师需要灵活调整教学方法。教师不能仅仅在课堂上为学生灌输“数形结合”思想，还应当结合学生在课后练习中的“成果”进行分析，以此来有效培养他们“数形结合”的思维能力。同时，教师在教学过程中，应当有针对性地为学生设置相关的学习情境，使学生通过相关学习更加透彻地理解数形结合思想。这样，学生就可以较好地把数形结合思想和现实中的实际问题结合起来，以数形结合思想解决现实中的数学问题。

从本质而言，数形结合思想就是将“数”与“形”很好地结合起来，从而使学生在解决实际问题时，能够合理分析其中一些复杂因素，进而使看似复杂的问题得以有效解决。 在小学课堂上广泛地应用数形结合思想进行教学既能有效提高学生对知识的掌握情况，又能在一定程度上培养学生的空间思维能力，使学生解决实际问题的能力得到有效提升，提高学生的数学素养。总之，教师教学时不应该仅仅停留在教学表面，而应当深入探究。“数形结合”的数学思想在当今小学数学课堂教学中的运用，使学生学习不再枯燥乏味，学生的逻辑思维能力得到有效加强，从而真正实现学生在课堂学习中的全面发展。