少样本条件下的电缆局部放电模式识别

岳云飞，孙 抗，2

（1.河南理工大学 电气工程与自动化学院；2.河南省煤矿装备智能检测与控制重点实验室，河南 焦作 454003）

0 引言

电缆是配电网及大规模清洁能源接入的关键基础设备，其可靠性关系到电力系统的安全稳定运行。我国日益增长的对更清洁、更低碳的绿色电网的需求使电缆在电力系统中扮演着愈发重要的角色。局部放电是电缆绝缘劣化的重要表征，对于不同类型的绝缘缺陷，其局部放电的表征也有所区别［1］。通过识别局部放电模式，获知电缆绝缘缺陷类型，可为评估电缆绝缘缺陷风险，逐步实现状态检修提供可靠依据［2］。

随着电力大数据时代的到来，深度学习将在电力行业具有广阔的应用前景［3］。由于电缆运行时故障发生频率较低，且故障案例与异常样本信息存在缺失、不完善等问题，现有有效标注的样本规模较小，严重影响了深度神经网络分类器的识别效果。业内学者针对少样本条件下的局部放电模式识别进行了大量研究，总体上可分为基于数据增广的学习方法与基于模型简化的学习方法两大类。

基于数据增广的少样本学习方法多借助先验知识扩大样本规模或平衡样本类别，如随机过采样算法（Random Oversampling，ROS）、合成少数类过采样方法（Synthetic Minority Oversampling Technique，SMOTE）等。刘云鹏等［4］采用一种基于梯度惩罚优化的条件式Wasserstein 生成对抗网络模型，有效增广了少数类样本。随着Alex-Net、VGGNet、GoogLeNet 以及ResNet 等深度卷积网络模型逐步应用于局部放电模式识别，局放样本不足的问题愈加突出。刘文浩等［5］提出一种基于可变噪音的局部放电样本扩充方法，缓解了局部放电样本数目不足的问题。史晋涛等［6］则利用图像合成技术扩充样本数目，提高了深度卷积网络模型的识别效果。

基于模型简化的方法一般通过减少分类模型的训练参数，提高分类模型的搜索效率。苑津莎等［7］通过降低特征参数的维数与简化概率神经网络分类器结构的方法，提高了分类器在少样本情况下的识别率。Liu 等［8］采用迁移学习的方法，缓解了深度卷积网络模型在少样本条件下的梯度消失问题，在提高网络模型识别精度的同时，减轻了模型计算和存储的压力。Liu 等［9］在少样本条件下，设计了一种只有3000 多个参数的超微卷积神经网络，显著降低了网络模型的复杂度。

对于少样本条件下的电缆局部放电模式识别，本文从数据增广与模型简化两方面入手，针对局部放电相位分布模式（Phase-Resolved Partial Discharge，PRPD）灰度图提出一种基于深度卷积生成对抗网络（Deep Convolution Generative Adversarial Network，DCGAN）的数据增广方法，并构造了基于盒维数的评价指标衡量生成样本的有效性。在模型简化方面，以深度残差网络为基础，分别从残差模块、网络深度两个方面简化深度残差网络（Deep Residual Network，ResNet）结构，使其匹配小规模局部放电数据集。

1 基于DCGAN的数据增广

1.1 DCGAN原理

DCGAN 主要由生成模型与判别模型组成。生成模型可将输入的随机变量变成与真实样本类似的生成样本，判别模型则通过学习真实样本的特征来鉴别生成样本是否真实［10］。两个模型经过零和博弈，最终达到纳什均衡［11］。DCGAN 博弈目标函数如式（1）所示：

式中，x表示真实样本，Pr(x)是x的概率分布，z表示噪声输入，Pg(z)表示z的概率分布，G(z)表示生成模型产生的生成样本，D(·)表示判别模型判定该样本为真实样本的概率。

对于生成模型G，希望其能生成与真实样本相同的样本G(z)，即数学模型D(G(z))=1，1 -D(G(z))=0，从而最小化模型G。损失函数如式（2）所示：

对于判别模型D，希望其能准确地判断输入的样本为真实样本还是生成样本。输入真实样本x时，数学模型D(x)=1，输入生成样本G(z)时，数学模型D(G(z))=0，即最大化模型D，损失函数如式（3）所示：

DCGAN 生成模型利用反卷积的方法将随机变量生成一组PRPD 灰度图，生成灰度图与真实灰度图将由判别模型来判定，判别模型的判别结果反向传播，并进一步优化生成模型与判别模型，最终生成模型产生使判别模型无法准确判定的PRPD 灰度图。DCGAN 作为一种由GAN 发展而来的一种新模型，其特点是利用步长卷积代替上采样层，充分发挥卷积层能提取样本深层次特征的优势［12］。

1.2 基于盒维数的生成样本质量评价

利用评价指标衡量生成样本的质量，是判断数据增广技术是否有效的重要方法。在图像识别领域，常选择Laplacian 梯度［13］、灰度方差函数等指标，这些指标通过评价生成样本的清晰度来判定生成样本的质量，指标数值越大，表明生成样本的清晰度越高。对于电缆PRPD 灰度图，其真实样本的清晰度偏低，所以生成样本的清晰度也偏低，导致这些指标对灰度图生成样本质量的评价效果一般。因此，文中提出一种基于盒维数的生成样本评价指标，通过衡量生成样本与真实样本的特征相似性，判断生成样本的质量。

盒维数作为一种分形特征，因具有易于经验估计、程序化计算等优点而常被应用于灰度图像的特征提取［14］。针对同一类型的PRPD 灰度图，分别提取其真实样本与生成样本的盒维数，对比其数值。盒维数的数值差越小，生成样本的特征与真实样本的特征越相似，即生成样本的质量越好。盒维数的计算方法如下：

将PRPD 灰度图用曲面z=f(x，y)表示，其中，z表示图像像素的灰度值，x和y表示图像各像素的位置。将整个x-y图像平面分成大小为r×r的网格，每个网格对应于三维空间中一叠大小为r×r×r的盒子，设在(i，j)的格子中，PRPD 灰度图的灰度最大值位于第l个盒子内，最小值位于第k个盒子内，则在第(i，j)个网格中，覆盖灰度图曲面的盒子数为：

所有网格中的盒子总数为：

式中，r 为盒子尺度，在不同盒子尺度r下，可计算得到不同的盒子总数Nr，从而得到序列(r(i)，Nr(i))。将序列(r(i)，Nr(i)) 表示在双对数坐标系上，得到对数序列(logr(i)，logNr(i))，进而确定对数序列的分形无标度区。在分形无标度区内采用最小二乘法计算对数序列(logr(i)，logNr(i))的负斜率，此负斜率即灰度图盒维数DV。盒维数DV的计算公式如式（6）所示：

2 结构简化的残差网络

2.1 深度残差网络

为缓解卷积神经网络因网络加深而出现的网络退化、梯度消失等问题，何恺明等［15］在卷积神经网络中引入恒等映射的设计，创造性地发明了深度残差网络。深度残差网络是以深度卷积网络为基础，并增加了残差模块的网络［16］。图1（a）表示无残差模块的卷积神经网络的隐藏层，将输入x经卷积等操作后，转换为期望输出H（x）。卷积操作如下［17］：

图1（b）所示残差模块一是残差网络模型中最常用的残差模块，与图1（a）最大的不同是，在其基础上引入了恒等映射，并使用批标准化（Batch Normalization，BN）和ReLu激活函数，从而使实际输出变为：

F(x)是输入x经转换得到的残差函数。引入恒等映射后，网络由原来x到H（x）的映射，转变为学习F(x)和x的加和，在提升模型学习能力的同时，也简化了模型的训练难度［18］。

残差模块一直接将输入x与F(x)加和，则必须保证输入与输出的特征图维度相同，其缺点是不易提取样本的深层次特征。图1（c）中的残差模块二与残差模块一的基本结构相似，但残差模块二采用了步长为2 的卷积层作为捷径连接，使其可以改变输入特征图的维度，从而使残差网络能从多个维度提取样本特征。

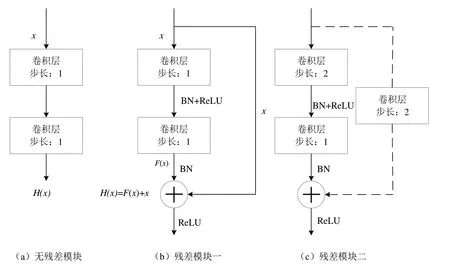
Fig.1 Different types of residual modules图1 不同类型的残差模块

2.2 残差网络的简化

虽然利用DCGAN 数据增广可以扩充电缆PRPD 灰度图样本数目，改善分类模型的识别效果，但与图像识别领域中的ImageNet 图像数据集相比，文中所构建的电缆局部放电数据集偏小。原始残差网络模型结构复杂，数据集规模与模型结构仍不匹配。为提升残差网络在少样本条件下对电缆PRPD 灰度图的识别效果，本文研究了有无残差模块、网络深度对残差网络的影响，并提出一种简化的残差网络模型。

2.2.1 残差模块对比分析

搭建了残差网络在含有残差模块一、残差模块二以及无残差模块三种情况下的模型。图2 描述了三种情况下网络模型的训练过程，图3为三种情况下网络模型的测试精度。

由图2 与图3 可知，具有残差模块的网络模型明显优于没有残差模块的网络模型。由于残差模块可以缓解梯度消失以及网络退化问题，因此减少了网络模型的训练损失，且提高了网络模型的识别精度。残差模块二通过对特征图进行升维或降维操作，避免了每一层的特征图都是相同维度的现象，因此残差模块二对模型性能的提升要优于残差模块一。

2.2.2 网络深度对比分析

Fig.2 Training process of network model图2 网络模型的训练过程

Fig.3 Test accuracy of network model图3 网络模型的测试精度

残差模块的个数影响着残差网络的深度，残差网络在具有不同残差模块个数下的测试精度如图4 所示。网络模型在含有2 个或3 个残差模块时，网络模型的测试精度在迭代10 次后趋于稳定，在含有4 个残差模块时需迭代20次以上才趋于稳定，这是由于网络结构过深时，网络模型需要训练的参数增多，所需训练时间也越长，因此测试精度波动较大。

2.2.3 简化后的残差网络

通过上述分析，搭建了一种能较好地识别电缆PRPD灰度图的残差网络，网络结构如图5 所示。简化的残差网络主要由卷积层、池化层、残差模块二和全连接层组成。网络中卷积核的大小选为3 × 3，在每次卷积操作后加入BN 层，并选取ReLu 作为激活函数。

2.3 基于简化残差网络的局放识别

基于简化后的残差网络模型，并结合DCGAN 数据增广，提出了基于DCGAN 与ResNet 的电缆局部放电模式识别方法，流程如图6所示。具体步骤如下：

步骤1：在实验室环境下搭建试验平台，制造4 种常见绝缘缺陷并采集局部放电信号。

Fig.4 Test accuracy of network model with different depths图4 不同深度的网络模型测试精度

Fig.5 Structure of simplified residual network图5 简化的残差网络结构

步骤2：提取有效局部放电脉冲的工频相位φ、放电量q和放电次数n，并构造4种绝缘缺陷类型的PRPD 灰度图。

步骤3：利用DCGAN 对PRPD 灰度图进行数据增广，将生成样本和真实样本组合为训练样本集。

步骤4：利用训练样本集训练结构简化的深度残差网络。

步骤5：利用结构简化的深度残差网络对测试样本集中的样本进行分类，得到识别结果。

3 实验与结果分析

3.1 数据集获取

搭建试验系统如图7 所示，该系统主要由升压部分、局部放电检测部分、电缆绝缘缺陷模型、示波器构成。

将连续200 个周期的局部放电信号转换为一张PRPD灰度图，如图8 所示，最终得到700 张PRPD 灰度图，4 种绝缘缺陷各占175 张。由图8 可知，主绝缘外表面划痕，主绝缘表面金属污秽以及外半导电层爬电三种绝缘缺陷的局部放电主要集中在180～270°之间，而绝缘内部气隙缺陷的局部放电主要集中于10°～90°之间。4 种电缆绝缘缺陷的局部放电特征与文献［19］所述基本一致，验证了试验的有效性。

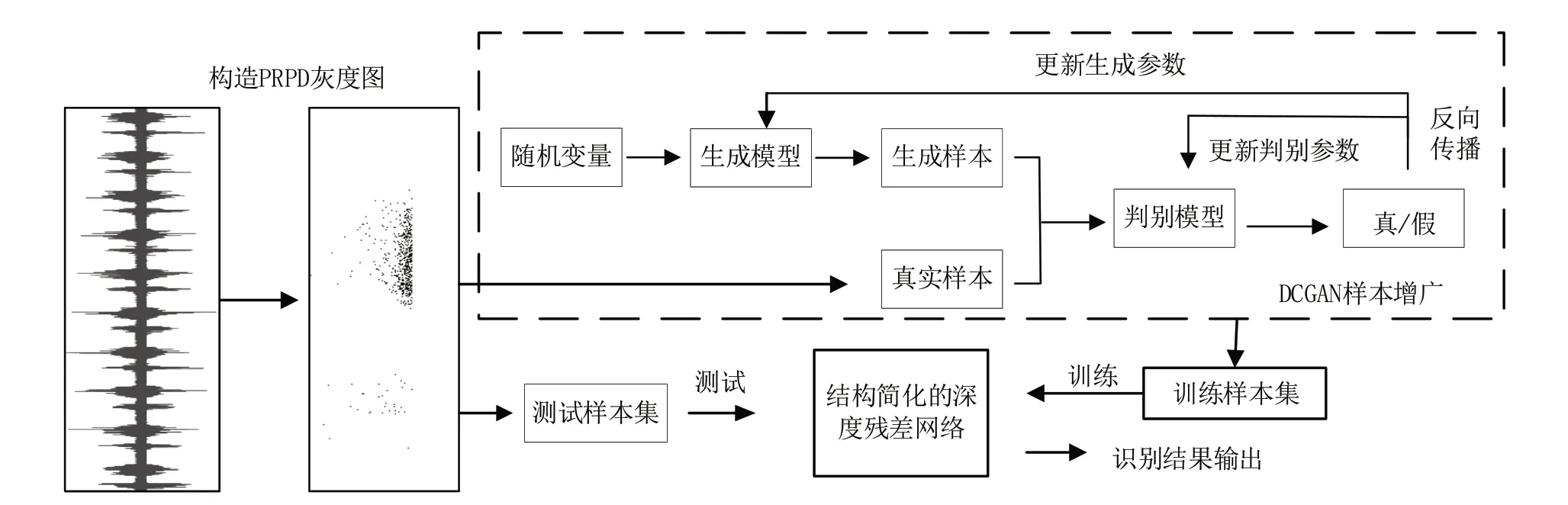
Fig.6 Flow of the algorithm图6 算法流程

Fig.7 Cable partial discharge detection system structure图7 电缆局部放电检测系统结构

将每类绝缘缺陷的PRPD 灰度图按5：2 的比例划分，即700 张真实样本被分为500 张训练样本与200 张测试样本。利用DCGAN 对500 张训练样本进行扩充，最终得到数目为1000 的训练样本集。测试样本集由200 张真实样本组成。

3.2 结果及分析

3.2.1 DCGAN数据增广的有效性分析

随机选取100 张真实样本和100 张生成样本，并分别计算其盒维数均值，如表1所示。

Table 1 Comparison of box dimensions of real samples and generated samples表1 真实样本与生成样本的盒维数对比

由表1 可知，4 种绝缘缺陷类型的盒维数具有明显差异，且分布在不同的数值区间。对于同一缺陷类型，生成样本的盒维数数值相近于真实样本，表明DCGAN 生成的样本与真实样本具有相似的特征。为进一步验证文中所提数据增广方法的有效性，设置了两个数据集：一是原始训练样本集；二是利用DCGAN 增广样本后的训练样本集。使用这两种训练样本集分别训练原始ResNet 和结构简化的深度残差网络，识别结果如表2所示。

Fig.8 PRPD grayscale images of four typical insulation defects图8 4种典型绝缘缺陷的PRPD灰度图

由表2 可知，对于结构简化后的残差网络，使用DCGAN 增广样本能大幅提高其模型的识别准确率，准确率达到了98.5%，与原始训练样本集相比，识别准确率提高了7%。不仅如此，原始ResNet 的识别率也因使用了增广后的样本集而得到提升，验证了DCGAN 数据增广的有效性。

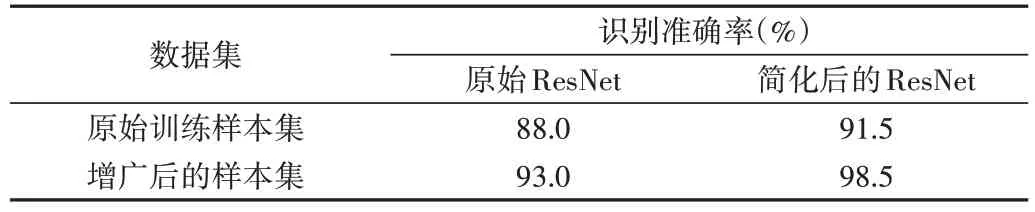
Table 2 Recognition accuracy before and after data augmentation表2 增广样本前后的识别准确率

3.2.2 简化残差网络识别结果及分析

利用增广训练样本集分别对简化后的残差网络以及原始ResNet 进行训练，采用Adam 优化器，初始学习率设为0.0001，最后使用测试样本集测试。两个模型的识别混淆矩阵如图9所示。

Fig.9 Confusion matrix of the two models图9 两种模型的混淆矩阵

从图9 可知，简化后的残差网络对爬电和气隙两种绝缘缺陷的识别率达到了100%，与原始ResNet 相比，简化后的残差网络提升了对划痕和污秽两种缺陷的识别率，分别提升了12.0%和6.0%。两种网络模型都容易将污秽缺陷误判为划痕缺陷，可能是由于这两种缺陷的局部放电灰度图相似度较高，导致模型误判。

在训练速度上，简化后的残差网络比原始ResNet 更具优势，两种模型的迭代速度如图10 所示。两种模型在首次迭代时所需的时间最长，且都呈现递减趋势。随着迭代次数的增加，每次迭代所需的时间趋于稳定。原始ResNet的平均迭代时间为86.5s，而结构简化的ResNet 的平均迭代时间仅为7.3s。这是由于简化的ResNet 仅含3 个残差模块，减少了模型训练参数，因此减少了模型的迭代时间。

3.2.3 与经典卷积神经网络模型的对比分析

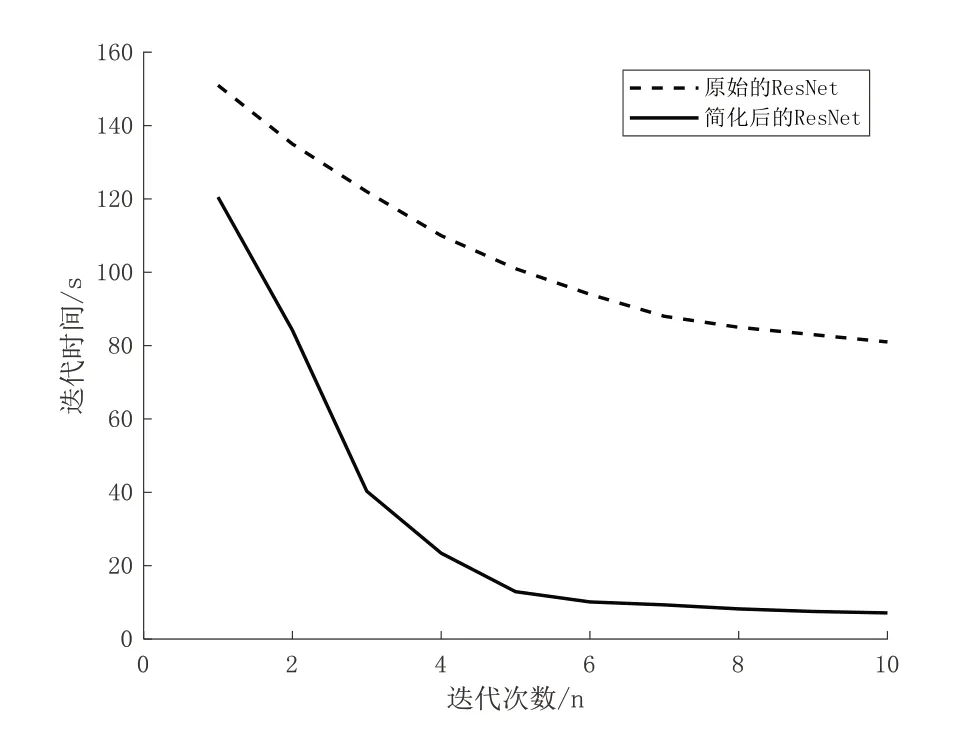
Fig.10 The training speed of the two models图10 两种模型的训练速度

为验证文中所提方法在电缆局部放电模式识别中的识别性能，搭建AlexNet、VGG-Net、GoogLeNet、ResNet 等具有代表性的深度卷积网络模型作横向对比。其中，AlexNet模型由5 层卷积层和3 层全连接组成；VGG 模型采用VGG-16结构，使用3 × 3的卷积核；搭建的GoogLeNet 模型为22 层，由2 个辅助输出模块和一个输出模块组成；ResNet 采用ResNet-18 结构。四种模型均使用增广后的训练样本集训练，各模型的识别准确率如图11 所示。实验结果表明，简化后的残差网络对PRPD 灰度图的识别准确率明显优于其他网络模型。由于VGG-Net 模型结构复杂，需训练的参数较多，导致其识别准确率较低，仅为79.5%。

Fig.11 The recognition accuracy of different network models图11 不同网络模型的识别准确率

4 结语

针对电缆PRPD 灰度图样本数目与深度残差网络结构不匹配的问题，提出了一种少样本条件下的电缆局部放电模式识别方法。在数据增广方面，文中通过深度卷积生成对抗网络将PRPD 灰度图的样本数目扩充了一倍，之后提取生成样本与真实样本的盒维数，并从特征相似性的角度评估了DCGAN 生成样本的质量。在模型简化方面，从残差模块和网络深度两个角度对原始残差网络的结构进行简化，最终设计了一种具有3 个残差模块的网络模型。实验结果显示，简化后的残差网络模型的训练速度更快，在PRPD 灰度图样本集上的识别准确率达到了98.5%，相比原始残差网络模型提高了5.5%。然而，文中仅对实验室条件下的4 种典型绝缘缺陷进行了有效识别，对于电缆现场各类故障的适用性仍需进一步研究。