基于神经网络算法的滚刀磨损量预测方法

丁小彬， 谢宇轩， 薛皓文， 李世佳

(1.华南理工大学 土木与交通学院，广东 广州 510640； 2.华南理工大学 华南岩土工程研究院，广东 广州 510640； 3.广州轨道交通建设监理有限公司，广东 广州 510010)

在硬岩地层采用盾构法进行隧道施工时，分布在刀盘上的盾构滚刀与岩面直接接触，是破岩的关键工具。滚刀的磨损形式和磨损快慢对施工进度和工程造价有很大影响[1]。磨损严重的滚刀会降低破岩效率，甚至导致机器损坏。目前开仓换刀仍需依靠工程经验人为判断[2]，具有较大主观性和不确定性。频繁开仓会增加工程风险、延误工期、增加滚刀采购成本与工程总造价。

当前滚刀磨损预测模型按照理论基础可分为经验公式和半经验公式。经验公式基于大量工程实践数据，通过经验系数反映各类复杂参数的影响，或通过岩石参数间比值关系[3]计算刀具磨损量。经验公式的使用范围深受数据影响，需要加以调整才可应用于类似工程项目[4]。半经验公式多数以金属摩擦学理论为基础，结合经验系数进行修正[5]，难以关联盾构施工参数，不利于及时判断刀具磨损状况。另一种思路是采用盾构中可快速获得的参数间接判断刀具磨损状态,常用的判断依据是盾构机的掘进速度[6]。

不论是公式计算还是间接判断，滚刀磨损预测难点在于其受盾构机管理、机械以及地质[7]等多方面因素的相互作用。该关系可以被简化为多元非线性问题，而神经网络算法具有强大的多元非线性分析能力，可作为研究滚刀磨损规律的有效方法。李笑等[8]结合Elman神经网络对掘进速度进行预测，并通过预测误差判断刀具磨损情况。陈子义[9]采用线磨损速率预测公式推算单环内的滚刀磨损量，分析相关工艺参数与滚刀磨损间的非线性关系。

边缘滚刀和中心滚刀的磨损还受偏磨和泥饼等附加因素干扰，而正面滚刀的磨损则相对规律，适合用于神经网络模型的训练[10]。复合地层中滚刀磨损研究还较为缺乏，滚刀偏磨频繁[11]，数据不利于进行滚刀正常磨损规律研究。

综上所述，从硬岩地层盾构正面滚刀的磨损规律入手进行研究，提出一种基于神经网络算法的滚刀磨损量预测方法，为现场施工提供较为准确的换刀时间及理论指导。

1 滚刀磨损量分析预测方法

1.1 算法原理简介

BP(back propagation)神经网络在人脸识别、自动驾驶、黑盒等复杂非线性问题上具有卓越表现，近八成涉及神经网络的研究课题以BP神经网络为基础方法[12]。

传统的BP神经网络存在诸如误差收敛速度慢、易陷入局部最小值、网络结构的确定缺乏可靠理论依据等问题[13-14]。采用各类优化算法可有效提高神经网络模型的表现[15-16]。本研究借助LM(Levenberg-Marquadt)算法进行参数更新，使用SMBO(sequential model-based optimization)方法搜寻模型最佳超参数组合。

LM算法在高斯牛顿算法的基础上增加阻尼系数μ以解决最小二乘法问题。该方法在迭代初期使用较大的μ，使梯度迅速下降；在迭代后期，使μ的值趋近于0，以实现参数微调，达到良好的收敛效果。

式(1)为一组阻尼系数调整方案，按增益比ρ来调整阻尼系数μ，ν为辅助放缩系数。重复上述过程，直至达到设定的尝试步数或模型预测误差小于目标值。

(1)

SMBO方法[17]是贝叶斯优化的一种形式化定义，该算法借助以往模型评估产生的参数及结果组成的历史信息，在指定的参数空间内快速搜索使目标函数取得最小值的参数组合；SMBO不需要进行梯度计算，具有较好的平滑性，支持多变量并行优化，被广泛应用于各类数据分析任务。

目标函数为BP神经网络的损失函数，所采用的SMBO方法借助TPE(tree-structured Parzen estimator)模型，以基于贝叶斯理论建立的高斯混合模型为替代函数；以常用的EI(expected improvement)为采集函数，选取下一组超参数。减少对目标函数的调用次数，提高超参数优化效率。

1.2 数据分析框架

在盾构施工过程中，通常数十至数百环开仓测量一次刀具磨损量，无法得知滚刀每环的磨损量。而盾构机在掘进过程中采集了大量对刀具磨损量存在潜在影响的数据。分析思路是将相对稀少的滚刀磨损量实测数据和丰富的盾构运转(管理)、刀具布置(机械)、地质条件(地质)参数关联起来，探究其中的联系，提高模型预测的准确性。

滚刀磨损量分析预测方法分为3个主要步骤，各步骤介绍如下。

(1)数据标定。排除原始数据中的异常值。以掘进环为最小单位，将各类数据统一为每掘进环一条数据。对每环有多个值的数据取代表值，对多环一个值的数据进行合理外推和插值。参考现有滚刀磨损量计算公式标定各环磨损量。

(2)模型训练。以BPNN算法模型为基础，采用LM算法优化BPNN模型的权值和阈值参数，再通过SMBO方法优化LM-BPNN算法中的部分超参数。

(3)模型预测能力评价。将预留样本输入神经网络模型中，对比神经网络模型预测磨损量和真实磨损量的误差，分析网络所学习到的规律，并对模型开发方案提出调整意见。

2 工程概况

广州市轨道交通18号线和22号线工程项目包含9个施工分部，其中18号线“番禺广场站—南村万博站”分段共包含1个中间风井和2个盾构井，该分段“番南2号盾构井—番南中间风井盾构区间”(以下简称“2—中区间”)是本文研究和分析所依托的工程背景，如图1所示。

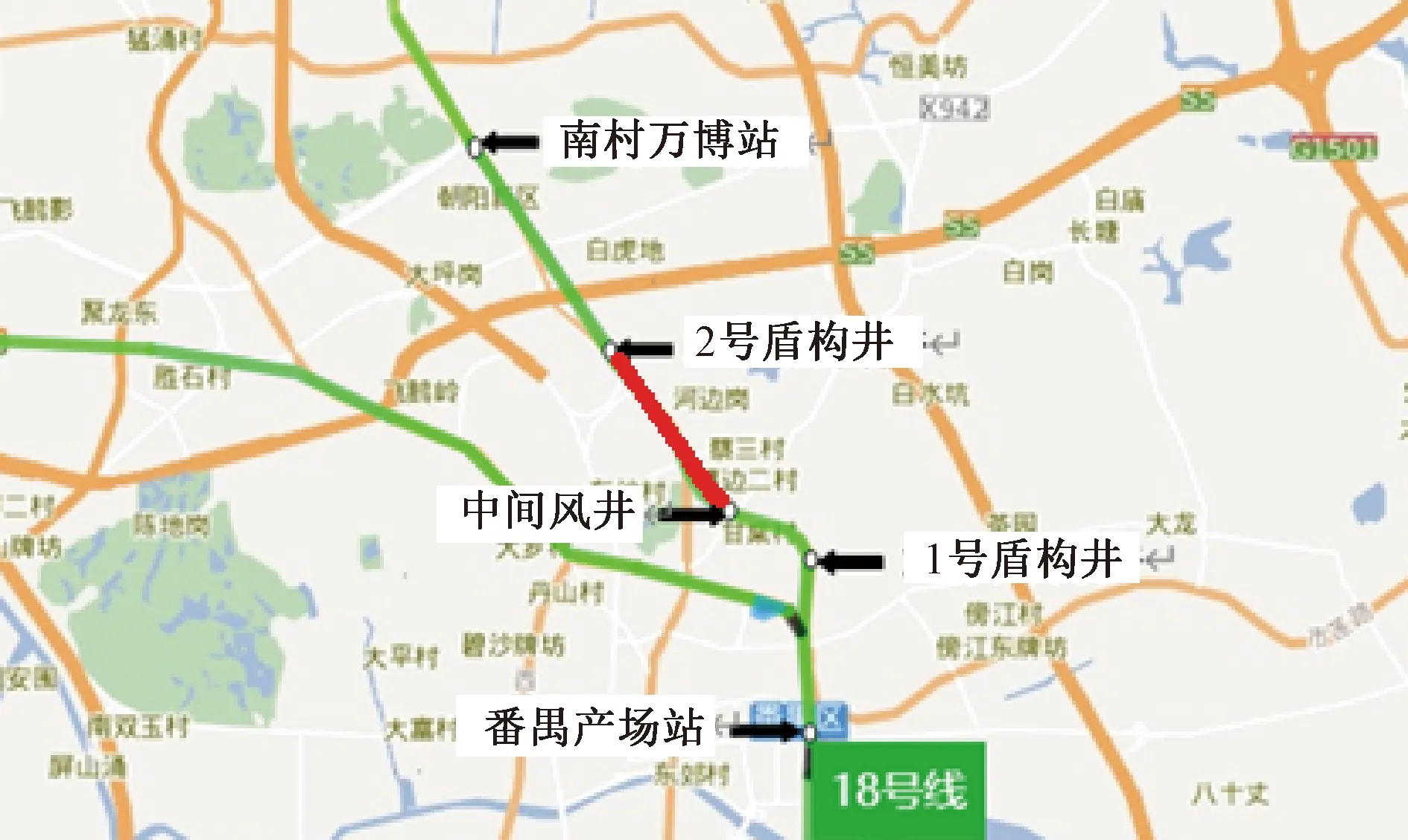
图1 番禺广场站至南村万博站盾构线网图Figure 1 Plan of tunnel section from Panyu Square Station to Nancun Wanbo Station

2—中区间由1 552环盾构管片组成，管片宽1 600 mm，即为每个掘进环的纵向长度；盾构途径地层以花岗岩和混合花岗岩地层为主，采用土压平衡盾构法施工。

原始数据来自365～523环，该区段开仓密集，地质分布较均匀，其地质剖面图见图2。该区段共159环，开仓 7次，将该段落划分为6个开仓段。图2中以虚线标出开仓位置并注明对应环号(365环为启始环)。阴影区域为盾构路线，途经中风化混合花岗岩(<8Z>)地层和微风化混合花岗岩(<9Z>)地层，折线为地层分界线。查阅该段落内钻孔勘探报告，未见不良地质现象。

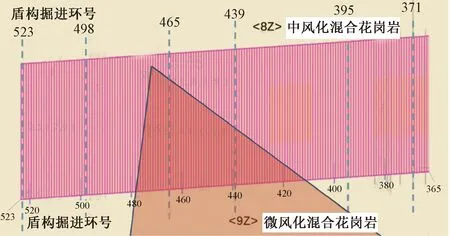
图2 番南区间右线365～523环地质剖面示意图Figure 2 Geological profile of ring 365 to 523 on the right line of Pan-nan section

3 数据分析框架有效性验证

3.1 数据获取

本研究将输入参数分为盾构掘进参数、滚刀机械参数、地质参数3类，分别反映管理、机械、地质因素。参考现有研究考虑的滚刀磨损影响因素，综合考虑数据来源以及施工实际情况，筛选3类共14种参数为输入参数，如图3所示。参数单位与采集系统保持一致，开发模型时将对数据进行归一化处理排除单位影响。

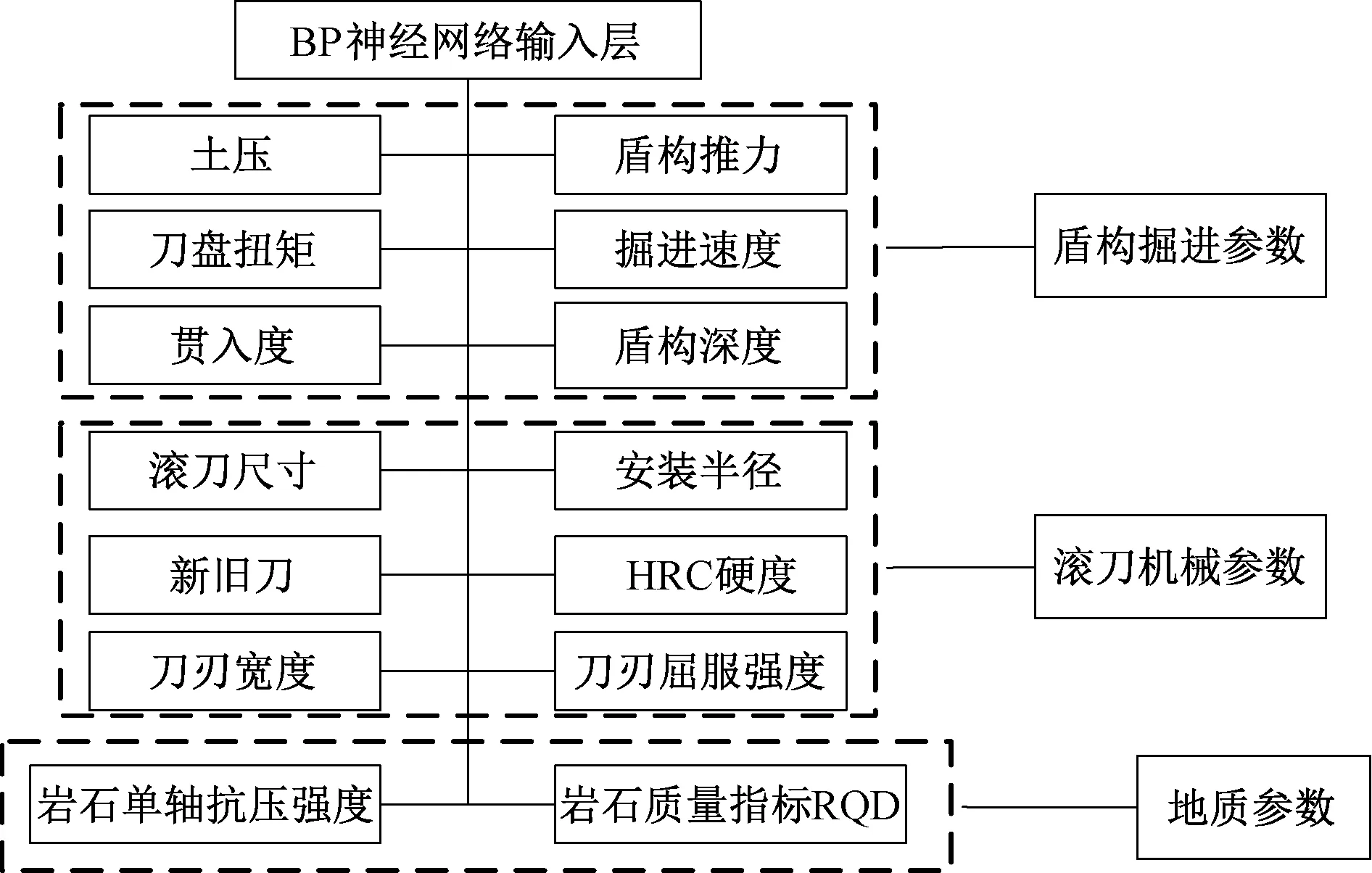
图3 BP神经网络输入层参数Figure 3 Input parameters of BP neural network

盾构掘进参数包括土压、盾构推力、刀盘扭矩、掘进速度、贯入度和盾构深度，均可通过广州地铁18、22号线盾构监控系统获取。该系统以秒为单位进行数据采集。将各环内掘进数据按照95%置信区间筛选并剔除奇异值，取剩余数据中值为各环掘进数据代表值录入数据集。

滚刀机械参数包括滚刀尺寸、安装半径、新旧刀、HRC硬度、刀刃宽度及刀刃屈服强度。滚刀尺寸和安装半径从DL523型刀盘设计图上获取，新旧刀、HRC硬度、刀刃宽度和刀刃屈服强度由施工方提供的刀盘刀具检测情况整理得到。因滚刀更换需要开仓，在两次开仓间的各环滚刀参数一般为常数。

地质参数包括岩石的单轴抗压强度和RQD值。参考详勘报告以及钻孔柱状附图，根据地层占比对地质参数做加权平均后用作各环地质参数代表值。

模型输出参数为滚刀磨损量，具体定义为刀圈半径的减少量，由工人在开仓检查时使用专用卡尺测量得到(图4)。受施工条件限制，无法直接测得滚刀单环磨损量。以盾构开仓时测得磨损量为准，参考杨延栋等[6]提出的正面滚刀正常磨损速率预测公式标定各环磨损量：

(2)

式中：ω为刀圈径向磨损量；Ks为磨粒磨损系数；S为刀间距；σc为岩石UCS；Ri为滚刀安装半径；T和σs为刀刃宽度与屈服强度；D0为滚刀直径；h为贯入度。其中磨粒磨损系数Ks与破碎颗粒的硬度、几何尺寸和数量等参数有关。参考赵海鸣等[18]滚刀磨料磨损的室内实验结果，代入已整理的工程数据集试算，当磨粒磨损系数Ks取80时，式(2)计算值与滚刀磨损量实测值误差较小。

图4 刀圈磨损量测量示意图Figure 4 Illustration of cutter ring wear measurement

标定单环磨损量时，将根据式(2)计算得到的磨损量根据实测值进行缩放。以正面滚刀S47为例，结合图5演示其具体步骤：按照开仓位置(由虚线表示)划分为多个段落，根据所选公式计算各环磨损量(由方形标记的折线表示)，将各段磨损量按照计算值之和与开仓实测值的比值缩放。开仓环号和对应磨损量见表1。标定结果用圆形标记的折线表示。

图5 滚刀S47单环磨损量推算Figure 5 Cutter wear labeling of each ring for cutter S47

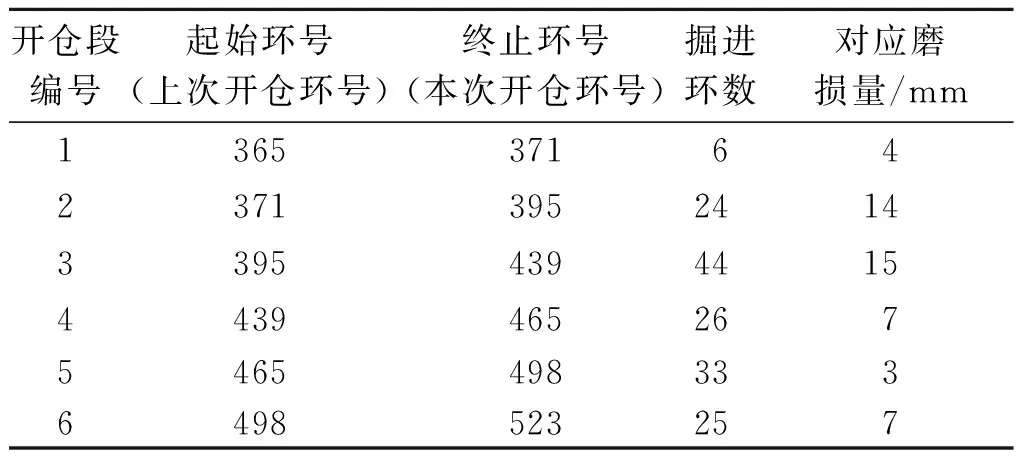
表1 滚刀S47磨损量分段统计表Table 1 Cutter wear of S47 in each section

本例中测量35把正面滚刀掘进共159环的磨损情况，经过上述步骤标定后获得159×35=5 565条数据样本。每条样本包含14个输入参数和1个输出参数，共计15个参数。但在实际工程中，部分正面滚刀存在刀圈崩裂、严重偏磨等非正常磨损，人工无法准确测量这类磨损。筛除这类数据后，获得形如2 386×15的矩阵作为后续模型开发数据集。表2展示了该数据集所采用的滚刀刀号和开仓段。滚刀S19所有区间磨损量均存在异常，故数据集中实际包含正面滚刀共34把。共采用81次实测磨损量进行标定。

表2 数据集滚刀刀号与盾构区间对应关系表Table 2 Selected tunnel sections and cutters

为保证模型预测结果可与真实值比较，划分数据时将各开仓段内样本作为整体，随机将样本划分为训练集和测试集，并保证训练集样本量占比高于50%，以保证模型得到充分训练。

使用最大最小归一化，公式见式(3)：

xnorm=(x-xmin)/(xmax-xmin) 。

(3)

式中：xnorm为归一化值；x为原始值；xmin为最小值；xmax为最大值。处理后各参数数据均分布在0～1，消除了单位和量级对训练的影响，方便数据计算与二次处理。

3.2 模型训练与评价

Kolmogorov定理指出3层网络可以精确描述任意连续函数。构建1个包含1个输入层、1个隐藏层和1个输出层的神经网络。输入层的节点个数为14，对应14种输入参数。输出层节点个数为1，对应1种输出参数。激活函数为sigmoid函数，损失函数为拟合常用的均方误差函数，采用LM算法优化网络权值和阈值。

将隐藏层节点个数、LM算法阻尼系数和迭代次数3项超参数作为SMBO方法优化对象。SMBO优化目标函数为神经网络模型的损失函数。试算确定超参数范围，阻尼系数取值为2～10，步长为1；迭代次数50～200次，步长为10；隐节点数5～14个，步长为1，设定SMBO最大搜索次数为100次。

评价神经网络模型的拟合结果，通常使用均方差MSE以及决定系数R2，其计算公式分别为

(4)

(5)

开仓测得的滚刀磨损量是评价预测准确度的直观指标，因此将开仓段内预测磨损量累积值和实际磨损量间差值占实际磨损量的比值定义为“预测误差”，作为评价指标之一。最优超参数组合为隐节点数5个，阻尼修正系数为8，迭代130次，对应R2最高。

分别用式(2)和训练中表现最佳的模型预测测试集的滚刀磨损量。将测试集数据开仓段、滚刀号、实际磨损量、预测磨损量与预测误差列于表3。预测误差为正时，表明预测值高于实际值，反之公式预测值低于实际值。测试集共包含22个实测值，公式预测高估了8个，模型预测高估了5个。

式(2)对于15个实测值的预测误差绝对值大于模型预测。式(2)和模型的预测误差平均值分别为20.09%和11.24%。模型相较公式考虑了更多的影响因素，多考虑的因素可能提高了模型预测的准确度。

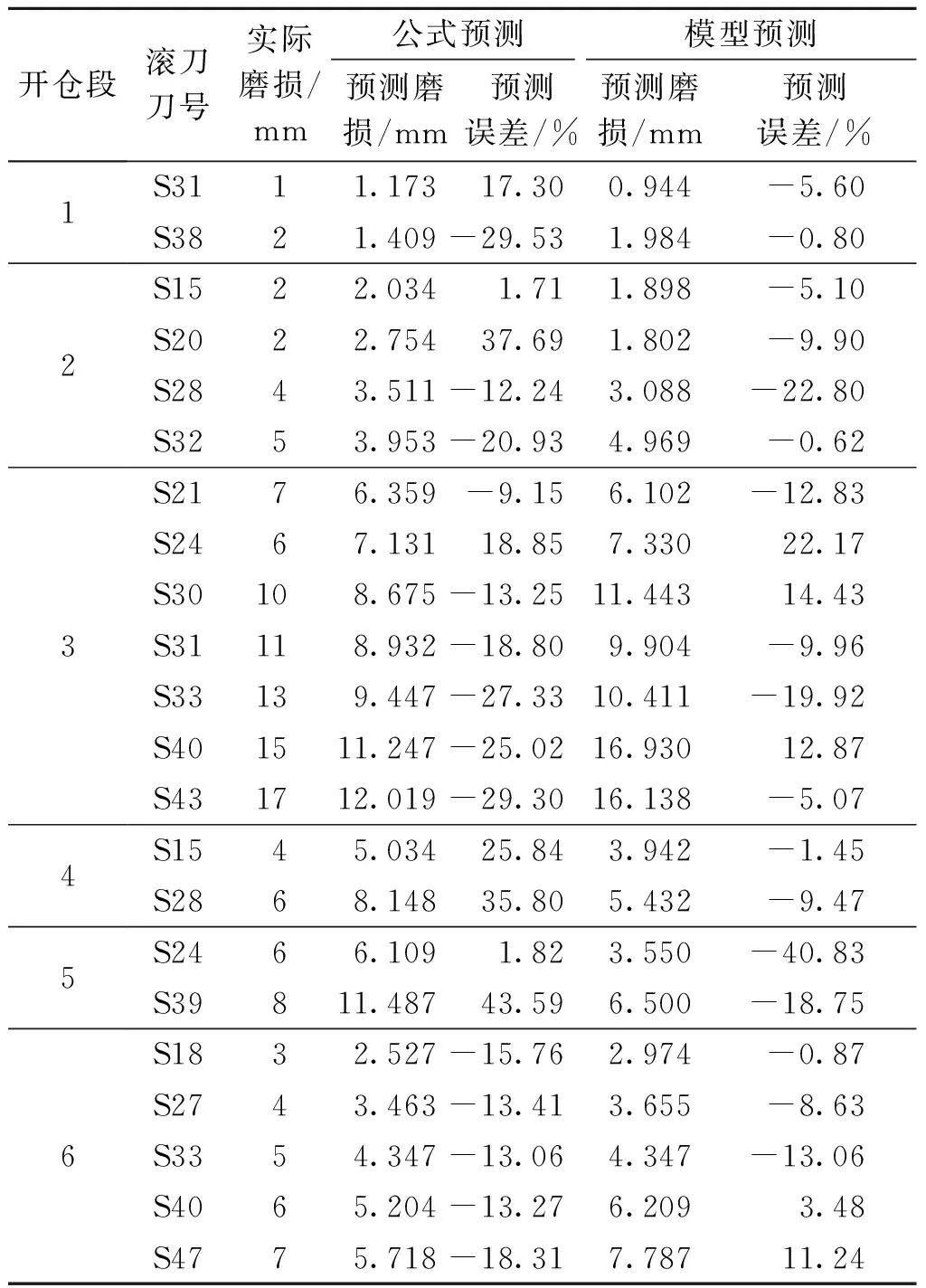
表3 区间滚刀磨损预测汇总表Table 3 Cutter wear prediction for each section

图6展示了各开仓段的决定系数R2和均方差MSE。开仓段1的R2高达0.992，对应的MSE仅有4.133×10-5；该区段内2、3、4、6这4个开仓段R2几乎一致，均在0.87附近，MSE则为20×10-5～40×10-5不等；开仓段3的MSE约为开仓段2、4、6的4～5倍；开仓段5的R2仅为0.636，显著低于其他段落，其MSE为423.5×10-5，相比MSE第2高的第3环高出近3倍。

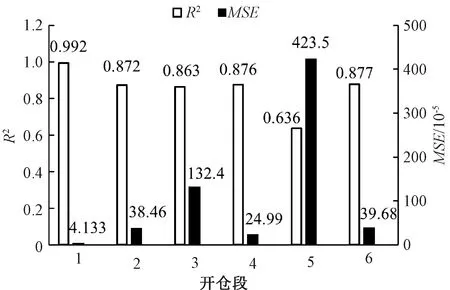
图6 开仓段评价指标Figure 6 Statistical evaluation of each section

R2和MSE反映出模型对磨损量的总体预测结果良好。虽然R2最高的开仓段具有最低MSE，且R2最低区段具有最高MSE，但其他区段的预测结果R2和MSE未见明显的相关性。

结合表3中预测误差和图2地质剖面进一步分析模型预测误差来源。开仓段3对应395～439环，共包含7把滚刀开仓数据，其中4把滚刀预测误差为负值。注意到图2中该区段微风化花岗岩地层占比沿掘进方向逐渐增加，在均匀变化地质条件下，模型倾向于低估磨损量。表3中开仓段5内各滚刀预测误差均为负数，反映该区段模型低估了滚刀磨损量。回顾图2中的地层组成，注意到该开仓段在465～480环区间内，掌子面上的岩层占比存在突变，导致模型低估该区段单环磨损量。可能的改进方法是细化磨损量标定的最小单位，例如构建数据集时以每分钟的掘进参数作为一条样本，从而让模型可以更充分地学习较为复杂地层下的磨损量积累过程。

4 结论

本文利用神经网络算法多元非线性拟合的优势，建立滚刀磨损量预测模型，综合考虑机械、地质以及管理3大类共14种参数对滚刀磨损量的影响，采用SMBO-LM-BPNN算法构建了滚刀磨损量数据分析框架，建立了尺寸为2 386×15的数据集。所得模型在测试集上的预测误差平均值为11.24%，采用的标定公式预测误差为20.09%。模型在测试集上5个区段的预测值R2超过0.86。进一步细化样本采样区间，或将所训练模型用于标定单环磨损量进行新一轮训练，有望进一步减小模型预测误差。

采用SMBO-LM-BPNN算法开发模型和公式标定单环磨损量，仅是当前案例下的一种可行组合。本文的数据训练仅局限于花岗岩地层，但所构建的数据分析框架具有良好拓展性，可结合工程特点采用其他易于获得影响参数和标定公式建立数据库。