复杂动态海面与目标电磁散射及回波仿真研究现状与展望

郭立新 魏仪文

(西安电子科技大学物理学院 西安 710071)

1 复杂海面与目标回波理论仿真研究现状

1.1 海面与目标复合电磁散射建模

复杂海面与目标回波仿真方法主要有两类：一是数学变换方法，通过描述散射场回波分布模型和功率谱，建立杂波的统计模型[1]。杂波统计特性的研究经历了如下发展：20 世纪 60 年代早期，采用高斯模型描述杂波，且杂波包络的幅度分布认为服从瑞利分布[2]；20 世纪 60 年代后期，由于高分辨雷达的出现，使用高分辨雷达探测杂波时，杂波分布经常会出现长拖尾的现象，因此逐渐采用对数正态分布取代瑞利分布描述杂波；20 世纪 70 年代至80 年代，在雷达高分辨率情况下，研究人员相继提出了能更好描述杂波分布的韦布尔分布和 K 分布。结合以上杂波数据分布模型，并采用零记忆非线性变换(Zero Memory Nonlinearity,ZMNL[3])或球不变随机理论[4]来模拟杂波回波，但以上杂波分布模型缺乏物理机理，且均是基于纯海面回波给出的，无法给出包含不同目标时杂波回波模型；二是散射仿真方法，即结合海浪模型和海面电磁散射理论，结合准静态模型，模拟海杂波。该类方法的物理意义更为完整，因为充分考虑到海浪和电磁波的相互作用机制，即建立不同时刻动态海面及目标的几何模型，对每一时刻海面与目标电磁散射特性采用散射算法进行理论仿真，这类方法具备更具体的物理意义，与实际更加符合。

复杂海面与目标复合电磁散射建模仿真方法可大致分为：低频数值方法、高频近似方法、高低频混合方法3类。

1.1.1 低频数值方法

低频数值方法一般通过直接求解特定条件下的积分方程或微分方程获得空间中的场分布[5]，无论粗糙面自身耦合，目标自身多次散射，还是目标与粗糙面之间的耦合都已隐含在算法当中。算法通用性较强且计算结果非常精确。低频数值方法一般有以下几类：矩量法(Method of Moment,MoM)[6-9]，时域有限差分方法(Finite Difference Time-Domain,FDTD)，时域积分方程方法(Time-Dmain Integral Equation,TDIE)[10-12]，有限元方法(Finite Element Method,FEM)等方法及其加速算法[13-21]。宾夕法尼亚州立大学 Wang等人[22]用MoM对粗糙面与上下方目标电磁散射特性进行了仿真。同时对粗糙面上部分埋藏目标[6]电磁散射特性进行了仿真。复旦大学叶红霞和金亚秋[9]分析了一维粗糙面及其上方目标电磁散射差场的计算，计算采用迭代MoM方法。由于MoM在建立阻抗矩阵过程中，任意两个单元之间的相互作用都要考虑在内，计算时间长且内存消耗大，对于实际电大尺寸目标与粗糙面复合散射问题，其效率非常低下。为了提高MoM的求解效率，国内外很多学者提出了相应加速算法：部分算法是通过加速求解阻抗矩阵实现的算法加速，如美国俄亥俄州立大学分别利用广义前后向迭代法(Generalized Forward Backward Iteration Method,GFBM)[23]、谱加速的广义前后向迭代法(GFBMSAA)[24]和多重扫描(Multiple Sweep Method of MoMents,MSMM)[25,26]对海面与漂浮目标复合电磁散射特性进行了仿真。阿肯色州大学KubickÉ等人[17]提出了基于MoM的快速算法-传播内层展开法(Propagation Inside Layer Expansion,PILE)，该方法保持了MoM计算精度高的优点，同时采用更高效的方法建立了阻抗矩阵，提高了计算效率。复旦大学金亚秋团队GFBM与谱加速算法(Spectral Acceleration Algorithm,SAA)结合GFBMSAA，仿真了半掩埋导体目标与介质粗糙面的散射特性[19]。部分学者借助集线器的思想，对MoM进行了加速，形成了快速多极子及多层快速多极子方法，EL-Shenawee采用最陡下降快速多极子方法(Fast Multipole Method,FMM)研究了二维粗糙面与三维目标的复合电磁散射特性。随着计算机硬件的发展，部分学者基于硬件设备，对数值算法进行了加速。图1为西安电子科技大学郭立新和王安琪等人[13,18,21]将MPI (Message Passing Interface)并行技术与FMM 技术结合得到的分层粗糙面与目标的电磁散射特性仿真结果及并行加速比。该课题组还采用高阶MoM分析了二维粗糙面与目标电磁散射特性，采用扩展传播内层展开(Extend Propagation Inside Layer Expansion,EPILE)[27]法对上下及漂浮目标共存时的复合电磁散射问题进行了深入研究。北京理工大学盛新庆团队[28]结合对偶积分方程和MLFMA分析了二维海面上方漂浮舰船的散射特性。另外，该团队还结合了GPU (Graphics Processing Unit)和CPU并行加速多级快速多极子算法求解特大电磁散射问题[29]。南京理工大学安玉元和陈如山等人[30]采用特征基函数展开和改进的交叉近似法对随机粗糙面及其上方目标复合电磁散射问题进行了研究。安徽大学黄志祥团队[31]采用基于MoM的渐进波形预估(Asymptotic Waveform Evaluation,AWE)技术计算了粗糙面宽带电磁散射特性。

图1 MPI并行技术与FMM技术所得仿真结果及并行加速比Fig.1 Simulation results and parallel acceleration ratios obtained by MPI parallel technique and FMM technique

FDTD方法[32-41]最早用于计算目标体电磁散射，Fung等人[42]将该方法用于粗糙面电磁散射仿真，并引入了高斯窗函数，以减小粗糙面在边界上由截断效应引起的电磁反射。Hastings等人[38]采用共形网格技术，灵活化地对包含大小尺度的复杂散射体进行不同精度的剖分，极大减小了FDTD方法的剖分网格数目。Turkel等人[43]提出了基于传统Yee网格的隐性差分方法。Krumpholz等人[44]则分别对电磁分量进行紧尺度函数和小波函数展开。Cole[45]采用非标准差分来近似空间导数。Shao等人[46]提出采用离散卷积差分方法来进行空间采样。国内复旦大学匡磊和金亚秋[37]采用FDTD方法计算了二维粗糙面上方/漂浮目标的电磁散射。任新成等人[47]采用FDTD方法分析了脉冲波源入射下粗糙面与多个半掩埋目标的散射特性。西安电子科技大学魏兵团队[48]利用FDTD对半空间中的天线罩近场特性进行了仿真。Liu[49]采用伪谱时域格式来进行空间采样。李娟和郭立新等人[34,35]采用并行FDTD分析了粗糙面及其上方目标的宽带散射特性。图2为HH极化与VV极化下海面与其上方圆柱复合散射并行FDTD、串行FDTD与MoM的比较。表1为串行FDTD方法与并行FDTD方法计算一个样本耗时对比[50]。

表1 串行FDTD方法及并行FDTD方法计算一个样本耗时对比Tab.1 Comparison of the simulation time of a sample by the FDTD method and the parallel FDTD method

图2 海面与其上方圆柱复合散射并行FDTD、串行FDTD以及MoM的比较Fig.2 Comparison of the sea surface with its overlying cylindrical composite scattering by parallel FDTD,FDTD and MoM

这些处理方法都可以在保证计算精度的同时，降低空间采样率，从而扩大时间步长的取值范围。

部分学者也采用有限元方法(Finite Element Method,FEM)[51-55]研究了粗糙面与目标复合散射特性。复旦大学刘鹏和金亚秋[54,55]将共形完全匹配层(Perfectly Matched Layer,PML)与FEM结合研究电大尺寸粗糙面上方以及漂浮目标的散射特性，并使用区域分解FEM分析了海面与上方飞行目标的电磁散射特性[55]及多普勒频谱特性[56]。郭立新团队[51,52]采用FEM-PML分析了介质粗糙面上方以及分层粗糙面下方埋藏目标的散射特性，并将FEM与BIM结合，用于粗糙面与目标复合散射研究。图3为本团队采用FEM计算的粗糙面和目标的双站RCS与感应电流分布。童创明团队[57]结合FEM-MoM与MLFMA两种方法研究了二维介质粗糙面上方三维介质目标的散射特性，进一步提高了计算效率。

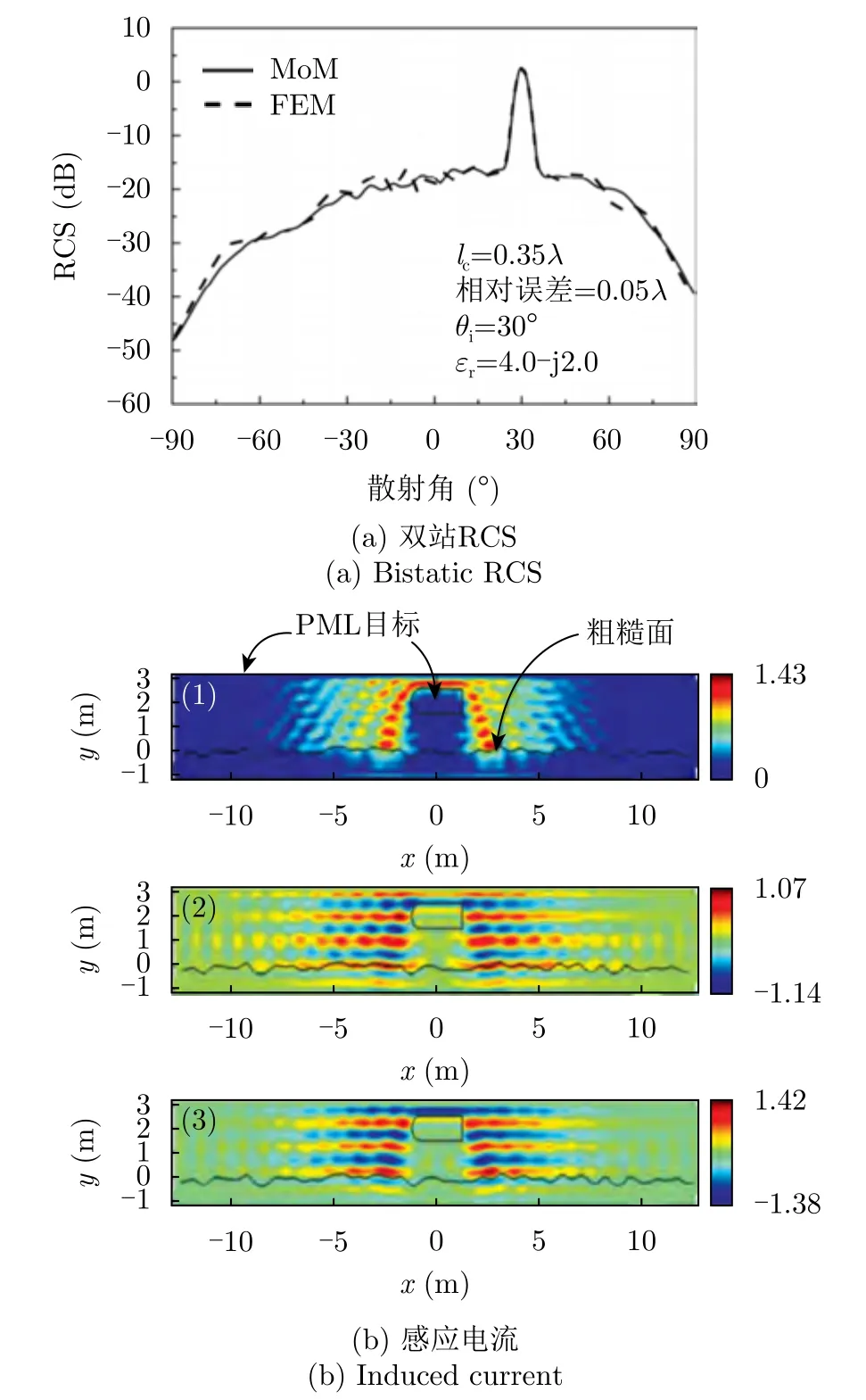
图3 FEM计算所得粗糙面与目标复合电磁散射仿真结果Fig.3 Simulation results of the FEM calculation of the composite scattering from the rough surface and the target

数值类方法极度消耗计算机内存，且计算时间长，尤其对于实际散射场景，通常雷达照射范围为几十米到几公里的海面，属于超电大问题，数值方法的计算时间往往难以忍受。并且杂波仿真要求对每一时刻每个复杂场景都进行仿真，使用数值方法几乎难以满足工程应用要求，近些年利用数值方法对杂波进行模拟仿真的工作几乎不再推进，大多数学者都转向使用高频方法或者混合方法来解决复杂海场景与目标散射问题。

1.1.2 高频近似方法

高频近似方法[58-63]通常基于电磁学中一些简化模型或者假设，其计算机内存需求小、计算效率高，虽然不及数值类算法精确，但对于电大尺寸电磁散射问题，其精度也能满足工程需求。因此，这类方法被广泛用于解决电大尺寸(尤其是超电大尺寸)粗糙面与目标复合散射问题。因为高频方法对散射机理的近似，采用高频方法时，需要考虑多种散射机制，以达到较高的精度。这就要求在复合散射问题中，不仅要考虑目标和复杂海环境各自对雷达照射波产生的面散射场，还要考虑目标和海环境之间复杂的耦合作用和多次散射作用机制。目标与粗糙面耦合的方法主要分为两类，一类为迭代电流类，一类是射线类。

迭代电流类方法的主要思路是：先得到粗糙面或者目标上入射场产生的第1次感应电流，然后考虑各面片散射对其他面元的影响，逐步迭代和修正第1次感应电流直至稳定值，最后将感应电流作为辐射源，计算散射场。迭代物理光学(Iterative Physical Optics,IPO)法最初用于自由腔体中耦合作用的计算，Sarabandi等人[64]其扩展到粗糙海面上，计算其散射特性。互异性原理(Reciprocity Theory)也能体现出目标与粗糙面之间的相互作用，密歇根大学Chiu等人[65-67]利用互易性定理简化了目标与地海背景耦合作用的计算。南京理工大学何姿和陈如山[68]用PO-IPO方法计算了海面与其上舰船的复合散射，但不断的面元之间的迭代作用也极为耗时，童创明等人[69]采用自适应迭代物理光学(Adaptive Iterative Physical Optics,AIPO)，降低了感应电流的迭代次数，提高了计算效率，对地面和近海临近区域上方目标的散射特性进行了仿真研究。电子科技大学杨伟等人[70]将IPO和PO-PO方法应用到目标与地海面复合电磁散射中。西安电子科技大学罗伟等人[71,72]将IPO应用到电大尺寸目标与地海面复合电磁散射中。西安电子科技大学李娟和郭立新等人[73]采用IPO研究了一维介质粗糙面与半掩埋目标的散射特性，随后郭立新团队又将PO-PO扩展到三维情形，研究了二维粗糙面上方涂覆目标的散射特性，图4即为计算三维粗糙面上方导体目标复合电磁散射RCS的迭代机理及与FE-BI-KA[74,75]仿真结果的对比[76]。结果显示两种算法吻合良好，证明了该算法的精确性。

图4 迭代电流类方法在复合散射中应用PO-PO与FE-BI-KA仿真结果对比Fig.4 The scattering comparation of two different current iteration methods: PO-PO and FE-BI-KA

但由于迭代电流类的方法依然需要考虑面片间的相互作用，如所有面片间的相互作用都考虑在内，其算法复杂度依然很大甚至堪比数值方法。以上多数文章都是由于在考虑耦合作用时进行了近似，才提高了一些计算效率。相较于迭代电流类方法，射线方法在考虑耦合时，本质上只对镜像反射引起的耦合进行了考虑，对多数工程场景，这样的精度也已经足够。但在漫反射较强的散射场景下，仍倾向于采用迭代电流类方法[77]。在已有射线类算法中最典型的就是“四路径”模型[58,59](Four-Path Model)，该模型在考虑目标与半空间耦合作用时，只考虑了4种路径下射线耦合类型。西安电子科技大学史小卫等人[78,79]与国立雅典理工大学的Anastassiu[80]在四路径基础上，提出一种闭型解析解求解无限大平板上方目标复合后向电磁散射问题。北京环境特性研究所董纯柱、王超等人[81]进一步针对微起伏粗糙面，结合镜像原理，扩展了四路径模型应用场景。北京航空航天大学许小剑等人[82-85]、西安电子科技大学郭立新、张民、魏仪文等人[86-88]对“四路径”模型进行修正，将“四路径”模型应用于目标与复杂背景复合后向电磁散射中。但该方法考虑海面与目标耦合时过于粗略，且在高海情时，难以获得准确结果。因此，国内外学者对弹跳射线(Shooting and Bouncing Rays,SBR)算法进行研究，考虑更多不同的路径耦合作用，在处理复合散射问题时更为精确。Jeng等人[63]利用SBR法分析了海面上方的舰船电磁散射，复旦大学徐丰、金亚秋[62]采用双向解析射线追踪(Bidirectional Analytic Ray Tracing,BART)方法计算了粗糙面与电大尺寸目标的复合电磁散射特性。在高频近似方法中，几何光学方法与物理光学方法由于忽略了电磁波边缘绕射机制，因此精度有限。对于多数目标，存在几何的棱边，这些棱边也会引起散射。大多数学者通过几何绕射理论(Geometrical Theory of Diffraction,GTD)[89]、一致性绕射理论(Uniform Theory of Diffraction,UTD)[90,91]、物理绕射理论[92](Physical Theory of Diffraction,PTD)进一步考虑棱边绕射机制，提高射线类方法的精度。

经过以上探索，为进一步提高SBR效率，满足工程实时性仿真需求，学者一般从以下两个方面提高其效率。一方面，射线追踪过程中，射线与面元求交过程最为耗时，部分学者引入树结构来提高求交效率，Tao等人[93]引入了KD-Tree技术加速了射线追踪的求交过程。部分学者通过光束分裂来减少射线数量，Park等人[94]将光束追踪技术应用于射线追踪算法，射线从发射平面只发出一束，在遇到不同的面元，才依据面元棱边信息，进行射线形状的裁剪，实现射线的自适应分裂。东南大学崔铁军团队采用BT算法分析脉冲平面波照射下的电大尺寸PEC目标的瞬态散射响应。另一方面，随着计算机硬件设备的发展，根据SBR算法射线独立的特性，采用GPU进行算法加速成为SBR算法非常适用的加速方式。根据GPU核数，计算效率可以得到几十几百倍提升。早在1993 年，Rius等人[95,96]就首次提出了利用显卡这一硬件设施来提高第1阶散射场的电磁计算问题。上海航天科技802所采用GPU加速的SBR算法研究了海面上方电大尺寸目标的复合电磁散射问题，大大提升了SBR算法的计算效率。西安电子科技大学郭立新团队也采用GPU加速的SBR方法计算了海面+目标电磁散射特性。以下分别为舰船目标和海面双站和单站散射(如图5所示)及其计算时间加速比(见表2)。

表2 仿真算例运行时间(秒)Tab.2 Simulation time (s)

图5 舰船目标和海面单双站散射Fig.5 Scattering from ship and sea surface

随着计算机图形学的发展，如OpenGL (Open Graphics Library)、OptiX等用于计算机图形渲染工具被开发出来。OpenGL是一个专业的图形程序接口，在游戏开发、虚拟现实、CAD仿真建模等领域都发挥着重要的作用，其图形渲染中用到的Zbuffer遮挡判断、面片裁剪等助于提高射线跟踪效率的优秀算法。OpenGL中物体映射到计算机屏幕示意图如图6所示。西安电子科技大学张民团队将OpenGL用于海面散射的遮挡判断，提高了SBR计算效率。西安电子科技大学范天奇[97]将OpenGL用于复杂目标电磁散射特性研究当中，该团队采用SBR计算了飞机目标(如图7所示)电磁散射特性，计算结果在图8中，算法中采用了OpenGL来加速射线追踪中的遮挡判断过程。

图6 OpenGL中物体映射到计算机屏幕示意图Fig.6 Diagram of object mapping to computer screen in OpenGL

图7 飞行器模型坐标示意图Fig.7 Schematic diagram of the aircraft

图8 电大飞行器双站散射结果Fig.8 Bistatic scattering of the aircraft

图7中模型角面片数量为158376，传统SBR计算时间和基于OpenGL-SBR算法计算时间对比如表3所示。

表3 仿真算例的运行时间(秒)Tab.3 Running time of the simulation example (s)

Optix是NVIDIA推出的射线追踪API，其最初设计目的是针对计算机图形学中的射线追踪问题。多用于游戏设计中的光线渲染，可帮助实现基于射线追踪的算法。Optix追踪射线的流程由以下几种程序(program)组成：(1)射线生成(Ray generation)；(2)异常处理(Exception)；(3)最近接触点计算(Closest hit)这个函数返回一根射线与目标面元最近的接触点；(4)所有接触点计算(Any hit)，该函数返回射线与目标面元所有接触点，可用于判断遮挡；(5)相交(Intersection)，是指射线与物体表面相交，Intersection发生在Closest hit处；(6)包围盒(Bounding box)，是指包括物体的最小立方体，这个是为了加速计算而特别设计的；(7)丢失(Miss)，没有照射到物体上的射线，用Miss程序处理。图9和图10分别给出了OptiX追踪射线的流程关系以及OptiX中各程序模块的关系及其数据交换的示意图。OptiX用于目标散射问题的射线跟踪策略是基于射线的，而不是基于面元的，因此在目标几何网格足够描述其几何精度条件下，并不需要对网格进行进一步划分，也十分适合处理非均匀网格模型。新加坡国立大学Temasek Lab的Wang等人[98]首次将OptiX用于计算复杂目标电磁散射快速预估，并利用SBR结合半空间格林函数分析了半空间中复杂目标的电磁散射特性[99]。郭立新团队还基于OptiX，实现了SBR算法加速，用于计算超电大目标电磁散射。

图10 OptiX中各程序模块的关系及其数据交换示意图Fig.10 Schematic representation of the relationship between the program modules and their data exchange in OptiX

以下给出了OptiX计算大型航母编队结果及计算时间。图11中包含1艘尼米兹级航母，长约344 m，最宽处93 m，高62.98 m；1艘指挥舰，长207 m，宽约32 m，高40 m；4艘阿利伯克级驱逐舰，长152 m，宽41 m，高53 m。总计面片数979025，顶点数540343。仿真了入射频率f=14 GHz，入射角θi=45°，入射方位角φi=0°，散射角从0°～360°变化以及入射角θi从-90°～90°,φi=0°的单双站散射结果以及计算时间分别如图12和表4所示。

表4 大型航母编队计算时间(秒)Tab.4 Simulation times for large carrier formations (s)

图11 大型航母编队示意图Fig.11 Diagram of a large aircraft carrier formation

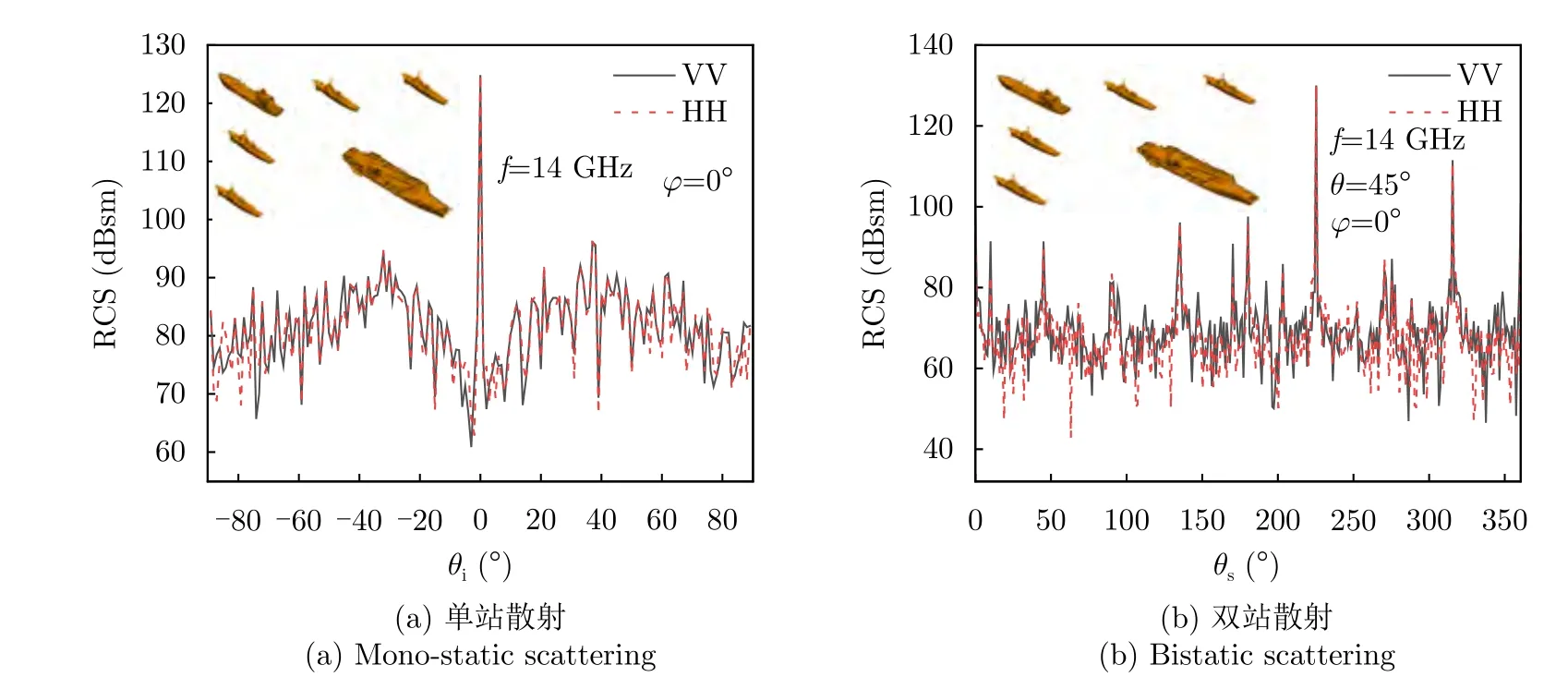
图12 大型航母编队单双站散射结果Fig.12 The scattering results for large carrier formations

实际雷达对海探测发射的信号在频域上是宽频信号，在空间上通常具备一定的波束形态，并不是平面波。对于实际的信号波形，采用频域SBR[100]需要扫频计算，但时域算法天然具备宽带信号散射的仿真能力，因此常被用于信号级回波仿真。东南大学崔铁军团队[101]将波束追踪(Beam Tracing,BT)技术引入时域射线追踪(Time Domain Shooting and Bouncing Rays,TDSBR)方法中，提出一种有效的时域BT-SBR方法来分析脉冲平面波照亮下电大尺寸PEC目标的瞬态散射响应。西安电子科技大学郭立新团队采用TDSBR方法仿真了复杂目标和粗糙面近场时域散射特性，并将OptiX应用于TDSBR中的射线追踪加速，给出了复杂目标时域回波信号。图13将TDSBR与CST软件中TD-FIT对简单舰船模型单站散射仿真结果进行了对比。入射角为(θi=90o,φi=0o)。调制高斯脉冲入射，中心频率为2 GHz，脉冲宽度为2 ns。仿真结果如图13所示，可以看出TDSBR与数值算法吻合良好[102]。

图13 TDSBR与CST时域回波仿真结果对比Fig.13 Comparison of TDSBR and CST time domain echo simulation results

图14给出了复杂舰船目标与海面场景示意图。图15给出了该场景在调制高斯脉冲机理下的散射回波随信号带宽(或脉冲宽度，调制高斯脉冲带宽与脉冲宽度关系为τ=4/Br)下回波时间序列。信号载频为f0=6 GHz，入射角为θi=30°,φi=0°，带宽分 别 为Br=4.0 GHz,Br=2.0 GHz,Br=1.0 GHz,Br=0.5 GHz。从图15可以看到随着脉冲宽度增加强回波处信号包络宽度增加。图16还给出了随着不同反射次数下散射回波结果。反射次数rfmax分别取1,2,3,4。可以看到只计算一次反射时，总体回波强度较小，考虑多次反射时，由于目标自身及目标与海面之间的耦合，回波结果上出现了一些散射强点，且回波幅度整体强度变大。在3次散射时，更多的散射强点出现，这都是因为较强的多次反射引起的，在反射次数为4次时，基本结果和考虑3次反射结果差异不大，说明该场景下，几乎没有4阶反射分量，一个场景下，射线能经过几次反射取决于场景几何模型的复杂度，该场景中海面与舰船组成的几何模型，几乎不会有射线在其中反射超过4次。

图14 舰船与粗糙面复合散射示意图Fig.14 Schematic of composite scattering from a ship and a rough surface

图15 不同带宽(或脉冲宽度下)调制高斯脉冲时域回波Fig.15 Time domain echoes of modulated Gaussian pulses under different bandwidths/ pulse widths

图16 不同反射次数时域散射回波Fig.16 Scattered echoes in time domain under different number of reflections

西安电子科技大学郭立新等人[103]、张民等人[104]利用SBR法结合半确定性面元法(Semi-Deterministic-Facet-Scattering Model,SDFSM)分析了导弹、舰船等军事目标以及涂覆目标与下方海面复合电磁散射特性[105]。新加坡国立大学Temasek Lab的Wang等人[99]利用SBR结合半空间格林函数分析了半空间中复杂目标的电磁散射特性。图17(a)为SBR结合SDFSM方法与(MLFMM)仿真所得目标与下方平板面复合散射RCS对比，与MLFMM对比显示，该方法具备较好的精度。图17(b)为利用SBR和SDFSM方法计算所得海面与舰船复合散射RCS结果[97]。

图17 SBR方法验证与仿真Fig.17 Validation and simulation of SBR method

基于以上电磁散射算法，还可以对舰船与海面复合场景的一维距离像进行仿真。以下算例给出了阿利伯克级驱逐舰与海面电磁散射一维高分辨距离像(High Resolution Range Profiles,HRRP)结果。图18给出了阿利伯克级驱逐舰与海面复合场景示意图，其中雷达俯仰角为89.8°，中心频率35.05 GHz，带宽100 MHz，海面大小为400 m×400 m，雷达入射方位角为0°，计算结果为单站。计算不同目标转角下距离像结果。

图18 阿利伯克级驱逐舰与海面复合场景Fig.18 Arleigh Burke-class destroyer with sea composite scene

图19为3级海情，风速取5 m/s时，不同舰船方位下舰船以及舰船+目标的一维距离像。图中可以看到迎头入射(0°)、尾部入射(180°)和正侧方入射(90°)时海面对复合散射一维距离像影响较小，单纯目标一维距离像与复合散射一维距离像重合较多，因为这几个方向上，舰船本身散射远大于海面散射以及海面与目标耦合作用，故在HRRP中，舰船更为凸显。而在斜入射时，海面散射对舰船的影响作用逐渐凸显。

图19 3级海况不同舰船方位下舰船以及舰船+目标的一维距离像Fig.19 High resolution range profile of the ship and the ship+target for different ship orientations in three sea states

图20给出不同海面风速下，复合场景一维距离像对比。可以看到随着风速的增大，海面散射越强烈，如果目标本身散射较小，极可能淹没在海杂波中。

图20 不同海况下舰船与海面复合场景一维距离像对比结果Fig.20 Comparison high resolution range profile of the ship and sea surface composite scenes under different sea conditions

另外，在考虑海面电磁散射时“海尖峰(Sea Spike)”现象通常对海上目标，尤其是微弱目标识别会产生严重干扰，导致误判。一般认为，海尖峰产生主要来自高海情下海上波浪破碎现象，因此，建立海浪破碎几何模型并计算破碎波电磁散射特征有着非常重要的研究价值。West和电子科技大学赵志钦等人[106,107]利用射线法及矩量法研究了单个破碎波结构的电磁散射。West[108,109]通过射线方法模拟仿真，证明了破碎波的卷曲部分、波面与海面形成的夹角中存在的多次散射以及布鲁斯特角”效应是引起HH极化结果大于VV极化结果的根本原因，一定程度上解释了“海尖峰”产生的物理机理。西安电子科技大学郭立新团队[110]通过求解简化的流体水动力方程，模拟了卷浪的3D波形(如图21)，利用SBR-PTD方法研究了含单卷浪海面(如图22所示)的电磁散射特性，图23为利用SBRPTD方法计算所得含单卷浪海面RCS结果[110]与矩量法(Method of MoMent,MOM)计算结果对比显示，此类方法具备良好的仿真精度。图24是利用SBR-PTD方法计算了电磁波在不同极化方式时，含单卷浪海面后向RCS。

图21 不同时刻的破碎波Fig.21 Broking waves at different moments

图22 含单卷浪海面散射模型示意图Fig.22 Schematic diagram of a sea surface scattering model with breaking waves

图23 SBR-PTD方法与MoM计算结果对比验证Fig.23 Validation of the SBR-PTD against MoM

图24 SBR-PTD计算含单卷浪海面的后向RCSFig.24 RCS of single breaking wave using SBR-PTD

现有文献在计算复杂环境与目标的复合散射问题时没有考虑传播问题，而实际对海探测中，由于海面上海水蒸发引起空气折射率分布不均匀，形成蒸发波导，蒸发波导的存在影响着电磁波的传播、衰减等特性，进一步对待探测物理的散射特性产生影响。基于此，西安电子科技大学魏仪文和郭立新等人[111]针对蒸发波导环境中目标及复杂背景的电磁散射特性展开研究，从大气波导中电磁波传播机制出发，利用射线追踪算法，建立大气波导电磁波传播三维射线模型，并将蒸发波导环境下入射波的条件进行预处理，利用SBR算法，研究蒸发波导环境下目标与海面电磁散射特性。图25为电磁波经过波导传播后，在波导出口处场强分布，蒸发波导高度为20 m，初始场的幅度为E0=50 V/m，天线为全向天线，频率为10 GHz。从图中可以看出场强呈层状分布，这是因为大气修正折射率随高度也呈层状变化。并且由于传播损耗，在方向上，发射面中间的场强值略大于边缘的场强值。图26为蒸发波导影响下目标散射场功率分布，天线为高斯天线，与坐标原点距离为10 km，天线高度为50 m，3 dB波束宽度为 15°，蒸发波导高度为d=25 m，频率f=1 GHz。舰船尺寸如下：长31.5 m，宽5.0 m，高4.3 m。由图像可得，散射功率呈现层状分布，因为其入射场强也是层状分布，由于目标舰船的对称性，可以看出空间散射功率也呈对称式分布。

图25 波导出口处场强分布Fig.25 Field intensity distribution at waveguide exit

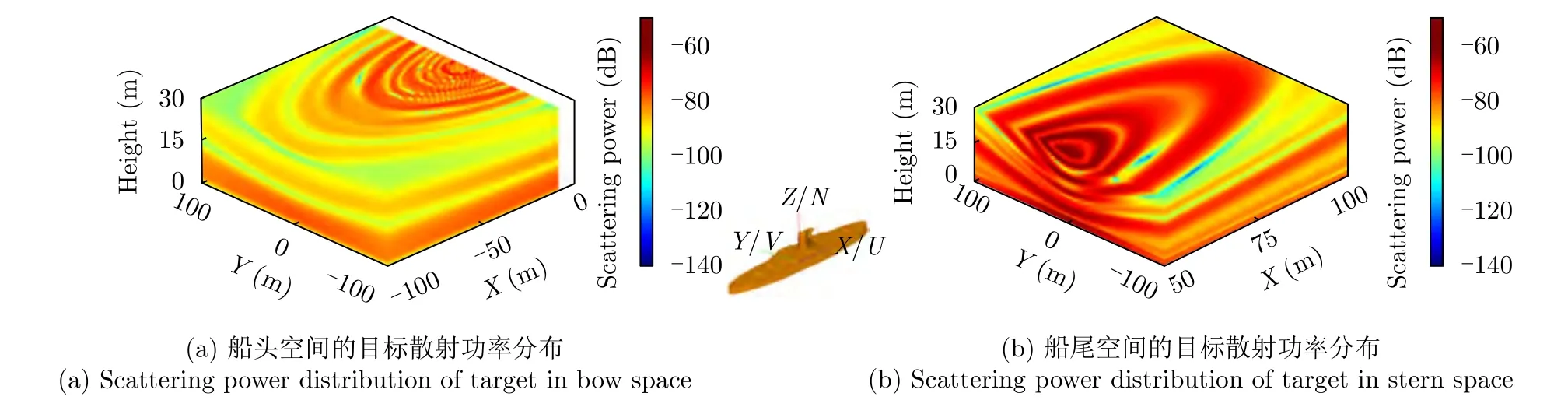
图26 考虑蒸发波导影响下目标散射场功率分布(船头旋转角φ=0°)Fig.26 Target scattered field power distribution considering the effect of evaporative waveguides (Bow rotation angle φ=0°)

1.1.3 高低频混合方法

国内外学者还提出了许多高低频混合方法。这种算法的初衷在于综合高频算得快和低频算得准的优势。美国麻省理工学院孔金瓯将采用MoM处理目标散射，采用微扰法(Small Perturbation Method,SPM)[112]计算粗糙面散射，并耦合两种方法考虑了粗糙面与目标的相互作用，计算了复合场景电磁散射特性。Bellez等人采用MoM-KA方法研究了介质粗糙面下方埋藏目标的散射特性，其中，对于含复杂结构的目标采用矩量法，并通过感应电流迭代，考虑目标与粗糙面耦合。东南大学张剑锋等人[113]提出MoM-KA方法，与Bellez方法不同，该文献主要通过半空间格林函数，考虑目标与粗糙面相互作用并对半空间中目标与粗糙面散射特性进行仿真。北京理工大学的盛新庆等人[114,115]进一步将MLFMA和KA算法结合，这样提高了目标部分电磁散射求解效率，也减少了耦合迭代时间。西安电子科技大学郭立新团队[116-118]通过对目标建立MoM的阻抗矩阵，对粗糙面散射的考虑体现在阻抗元素的修改，最终采用MoM-PO方法，仿真了目标与粗糙面的复合电磁散射，如图27所示。

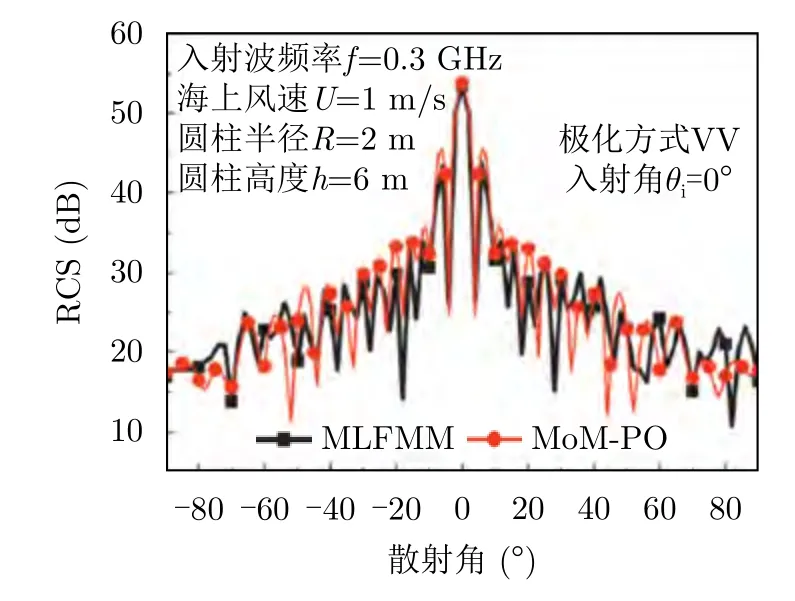
图27 MoM-PO海面与上方圆柱电磁散射仿真结果Fig.27 Scattering results of sea surface and cylindrical with of MoM-PO

电子科技大学杨伟和赵志钦等人[119]将MLFMA与KA结合研究了二维介质粗糙面上方三维目标的散射特性。空军工程大学童创明等人[120]提出针对高斯粗糙面与临空目标复合电磁散射的基尔霍夫-亥姆霍兹方程-MoM的混合方法。秦三团[10]采用TDIE方法结合时域基尔霍夫近似(Time-Domain Kirchhoff Approximation,TDKA)对一维导体粗糙面与二维导体目标复合瞬态散射进行仿真分析。复旦大学刘洋等人[121]基于有限元边界积分方法(Finite Element Boundary Integral,FEBI)和PO的迭代混合方法，用于求解电大规模平台的复杂结构的散射问题。

1.1.4 3类方法在复杂海面与目标电磁散射仿真中的可行性分析

下面对复杂海面与目标复合散射场景的电磁散射机制和特点进行分析(如图28)。(1)海洋表面是典型粗糙面，存在着小尺度毛细波，因此海面本身存在着较强的漫散射成分；(2)在高海情情况下，海面的波浪会产生卷曲和破碎效应，波浪的卷曲处存在电磁波的多次反射；(3)目标与海面之间因为电磁波多次反射存在电磁耦合作用；(4)目标面片的面散射；(5)目标面片多次反射。综合以上特点，仿真中算法需要既考虑海面漫射效应，也能考虑到面片间的多次散射及耦合作用，还能考虑到目标的面散射。

图28 复杂海面与目标散射成分分析Fig.28 Analysis of the scattering components from complex sea surfaces and targets

低频方法计算结果精确，无论哪种电磁散射机理，直接反射、面散射、耦合作用等，都已暗含在算法当中。算法通用性较强且计算结果非常精确。但是计算效率低下，适用于小区域下散射结果仿真，且对仿真效率要求不高的场景。对于电大以及超电大的海面与目标场景，通常面临着内存不足、计算效率低下的问题，难以用于工程应用。

高低频混合方法，一般对于结构较为复杂的目标采用低频方法计算，用以捕捉目标复杂结构之间的耦合作用，用高频类方法计算粗糙海面散射(如PO)，然后将目标和粗糙面之间的场进行迭代，以考虑海面与目标的耦合作用。这类方法，对电大尺寸目标，由于采用数值方法计算，依然存在计算效率低下问题，对粗糙面也仅考虑了海面与目标之间的耦合，且海面面片与目标面片两两之间考虑耦合，计算效率也会降低。在高海情时，存在的海面自身的耦合(破碎波引起)，而现有文献中高低频混合方法并未考虑。因此，高低频混合问题适合计算效率要求不高且海面海情较低的情况。

相较其他方法，高频方法耗时最短，效率最高，适应于工程中对电大尺寸场景电磁散射进行预估，但每一种高频方法都存在适应性的差异，且单一一种算法，难以考虑多种散射机制。对于海面与目标场景，需要考虑直接面散射、海面漫散射、目标自身耦合、海面耦合以及目标与海面之间的耦合作用。因此，寻求多种高频方法的组合，才能充分考虑海面与目标散射场景的各种机制，达到精确度的要求。

1.2 动态海面与目标复合散射回波仿真及分析

现有文献中对杂波统计特性的分析一般从两个角度入手，一种是对实测海杂波回波数据进行分析；另一种是采用数值仿真方法对复杂海面进行电磁散射建模，从而对海杂波的分布特性进行分析。国外由于技术设备先进，做了大量的海杂波实验，包括美国海军研究实验室(Naval Research Laboratory,NRL)的X波段雷达海杂波测量试验[122]，加拿大McMaster大学的X频段IPIX雷达海杂波测量试验[123,124]，南非科学和工业研究理事会(Council for Scientific and Industrial Research,CSIR)的X频段Fynmeet雷达海杂波测量试验[125,126]，澳大利亚国防科技署(Defence Science and Technology Organization,DSTO)的多波段(L,S和X波段)雷达海杂波测量试验[127-129]，英格兰南海岸多波段(S,X和Ku波段)雷达海杂波测量试验[130]，德国和法国联合开展的MARLENE (Mediterranean RFC and Sea Clutter Environ-mental Experiment)多波段(C,X,Ku,Ka和W波段)雷达海杂波测量试验等[131]。国内也有多家单位展开了海杂波及目标回波测量实验，海军航空大学推出雷达对海探测数据共享计划获取多种条件下雷达实测数据和试验辅助数据[132]。中国电波传播研究所通过岸基雷达对海探测，获取多波段下对海探测数据。实际对海数据中，虽然国内外各研究部门展开多项对海探测实验，但现有数据中大多数数据集并未公开。下面仅选取部分公开数据集进行介绍：

(1) 加拿大McMaster大学[123,124]在1993年公布的IPIX雷达(Ice Multiparameter Imaging X-Band Radar)数据集已经成为使用最广的数据集[133]。公开部分的数据集中，雷达架设在建安大东海岸，面朝大西洋探测。待测目标为直径1 m的浮标圆球。外场实验中，工作组将X波段的全相参雷达在一个高出海平面25～30 m的固定位置上，工作在驻留模式下，擦地角小于1°，观测时间为131.072 s，发射峰值功率为8 kW，该雷达对海面进行了大量的观测，面向海面的一个方位保持不变并进行持续观测，每次观测的时间大约2 min，而且还记录了大量海面漂浮目标的回波数据[134]，形成了IPIX雷达数据库[135]。1998年，McMaster大学对IPIX雷达的设计进行了改进，通过该雷达采集到的雷达回波数据为多种检测算法提供了验证依据，并且利用采集的海杂波数据在研究海杂波的特性方面也取得了进一步的进展。IPIX雷达是一个X波段的雷达系统，它具有双极化接收的特性，正是因为它的这种特性存在，该雷达能够几乎同时发射正交极化信号。表5描述了IPIX雷达的主要性能参数。

表5 IPIX雷达主要性能参数Tab.5 The key parameters of IPIX radar

图29为编号40数据不同极化的时空二维杂波图。IPIX距离分辨率为30 m，雷达照射区域覆盖14个距离单元。

图29 IPIX雷达编号40数据不同极化下时空二维杂波图Fig.29 Two-dimensional spatial-temporal clutter maps for different polarizations of IPIX radar number 40 data

IPIX雷达特点分析及使用建议：IPIX雷达数据集由于其开源的特性，在世界范围内，被很多难以开展对海杂波实际测量的研究团队使用。测量区域内，既有包含目标的分辨单元，也包含纯杂波单元，被广泛用于杂波特性研究和海上目标检测研究。但在其公开部分的数据中，待测目标较为简单(直径1 m的漂浮圆球)，且没有其他运动状态的待测目标。其次，相较于现今使用的高分辨雷达，IPIX数据中，使用的雷达分辨率较低。

(2) 南非CSIR协会于2006年在南非海岸利用X波段Fynmeet雷达采集不同雷达参数以及海洋环境的回波数据[136]，Fynmeet雷达安装位置为南纬34°36′56.52′′，东经20°17′17.46′′。Fynmeet雷达的距离分辨率为15 m，擦地角范围0.3°～3.0°，工作频率范围为6.5～17.5 GHz，发射峰值功率为2 kW。部署现场的平面图如图30所示，试验架设位置如图31所示，OTB的主要特性如表6所示。该实验中，有3艘合作船只用来记录回波数据等测量结果。

表6 OTB MS3的主要特性Tab.6 The main characteristics of OTB MS3

图30 部署现场平面图Fig.30 The deployment site plan

图31 试验架设位置Fig.31 The test stand location

相较于IPIX数据集，该数据集包含多个频率(6.9 GHz,8.0 GHz,9.0 GHz,10.3 GHz)，且覆盖多个天线方位角。对海面参数记录也较为完整，其中有气象站记录天气状况，且有定向浮标记录海面波浪高度、方向、周期等。综上，该数据集在参数多样性和参数记录方面较为完整。可用于杂波抑制与目标检测方法的性能评估。

(3) 海军航空大学刘宁波等人利用X波段固态全相参雷达架设于海岸边开展对海探测试验，对海探测实验点位于烟台养马岛附近海域，探测数据包含了海面回波、放置的浮标回波、岛岸回波，以及非合作中小型船只。如图32所示，该雷达的工作频率为9.3～9.5 GHz，擦地角范围为0.3°～315.0°，雷达工作模式为凝视或扫描状态，当该雷达处于凝视模式时，持续测量一段时间并且记录雷达回波数据，每组数据包括单载频发射信号以及线性调频发射信号[132]。本实验中所使用的雷达技术参数如表7所示[132]。图33是利用该数据绘制的杂波距离-方位图。

图33 距离-方位图Fig.33 2D graph of range-azimuth

表7 雷达参数Tab.7 The key parameters of radar

图32 对海探测实验点Fig.32 The experimental site for sea dection

该数据在我国海域内测量，相较于国外数据集，更符合我国海域特点。雷达采用多种模式，雷达入射波采用多种波形和脉冲发射模式，记录多种海洋气象水文信息，距离分辨率较高(6 m)，探测点多，探测多个区域海面。杂波中信息丰富，不仅包含海面回波信息，有些还包含岛屿，以及海上中小型船只。数据量大，覆盖参数范围广，杂波信息丰富。该数据集构建形成可以用于支持海杂波特性认知、海杂波抑制、海上目标检测跟踪与分类识别技术研究的数据集。

(4) 中国电子科技集团公司第二十二研究所多年专注地海杂波测量，具备多极化，海情覆盖1～5级，我国沿海不同海域及陆海交界区域，VHF,L,S,X,Ku等不同频段的杂波测试能力。通过灵山岛岸基雷达(如图34)，装备多波段雷达船只的船载雷达，以及海塔平台(如图35)等测量手段，获取大量对海杂波数据。目前数据对外公开。公开数据包含UHF波段和X波段，分辨率覆盖7.5 m,30.0 m,60.0 m。海情覆盖1～4级。该数据集主要探测纯海杂波，可用于杂波特性分析。

图34 灵山岛综合实验基地Fig.34 Lingshan island integrated experimental base

图35 海塔平台Fig.35 The sea tower platform

以上实验都形成了一系列杂波及杂波和目标数据集，为实际复杂海环境下目标检测提供了数据支撑，但限于成本和条件限制，测量数总是有限的，实际测量并不能覆盖变化的雷达参数(如载频、入射角、方位角、方向图等)以及不同的海洋参数(风速、风向、温度、盐度等)下的所有数据，总是存在一些条件下的数据缺失，因此，基于电磁散射机理的数据仿真成为一种低成本，且条件可控的海面及目标电磁散射回波获取方法。

最早根据海杂波测试数据得出海杂波随各影响因素变化规律的是美国海军研究实验室(NRL)[137]，文献[138]中分析了实测杂波数据，得出了威布尔分布和K分布在中等入射角下对杂波拟合较好，Senior与Hunter[139]在英格兰南海岸完成了海杂波的测量，研究了大入射角下，海杂波在风向与观测角度的影响下的衰减规律。国内众多学者也展开了实测杂波特性分析，西安电子科技大学吴振森等人[140]基于IPIX雷达实测海杂波数据以研究海杂波的分布特性。中国电波传播研究所从地海杂波的形成机理、测量与数据处理、地海杂波研究在雷达中的应用等方面对地海杂波进行了系统性的论述。

此外，很多学者采用仿真方法对海杂波幅度分布特性进行了研究。实际上对动态海面电磁散射特性的仿真研究是一项十分复杂的工作。首先，需要对不同海情下的动态海面进行建模。动态海面几何建模一般采用线性滤波方法，其基本思路是将海浪视为各种阶次的谐波成分的相互累加，这些成分的频域分量与海浪的高度起伏互为傅里叶变换对，因此根据选定的海谱形式求出频域分量后，利用快速傅里叶逆变换(Inverse Fast Fourier Transform,IFFT)这一过程即可求出与海谱类型相应的海面波高轮廓模型。该方法认为，在某一确定的时间点t，海面上任意一点高度起伏可以看作由于多个各向异性的正弦波的波动组合而引起的。但通过大量实际海浪数据的实验与研究发现，海浪的分布是存在不对称性的，即海浪各阶次的成分波之间的非线性水动力相互作用的存在，使得海浪的真实相干作用并非停留在单纯的线性融合基础上。1994年Creamer等人[141]提出在线性海面为基础的前提下，改进线性表示法，从而得到非线性海面模型。该Creamer模型建模得到的海面具有相对于同物理仿真参数下的线性模型更为“平坦”的波谷与“高耸”的波峰。同时随着风速进一步增大，海面非平稳性增强，随着不断加强的波流相互作用，海上会出现波浪的卷曲和破碎现象，美国加州大学基于海洋动力学原理通过数值方法求解得到了碎浪的几何模型，即LONGTANK破波模型[142]，该模型被广泛用于碎浪模形研究。国内电子科技大学赵志钦团队[143]将二维 LONGTANK 卷浪模型中不同时刻的卷浪进行拼接，生成了三维破碎波。张民等人[144]利用曲面劈模型模拟中等尺度的破碎浪。西安电子科技大学郭立新团队通过求解简化的流体水动力NS方程[125]，模拟了卷浪的3D波形及其随时间变化过程。其次，回波仿真方法还要考虑超电大尺寸海面及不同时刻、不同状态下众多海面样本回波带来的计算量大的问题。Arikan[145]采用数值方法模拟了不同频率下的海杂波并分析了频率对海面雷达回波分布的影响。Soriano等人[146]研究了L波段下二维动态海面的多普勒回波频谱。Toporkov等人[147-149]采用准静态方法对动态海面电磁回波特性进行了研究，并比较了电磁计算方法对动态海面多普勒回波特性的影响。西安电子科技大学郭立新团队丁慧芬[150]建立了动态海面与目标复合散射模型，仿真了回波的分布特性，寻找不同海面参数及雷达参数下，杂波分布的最佳模型，并对分布参数进行了估计，还仿真了杂波的多普勒特性和混沌特性。

图36给出了不同风速下的海杂波拟合的幅度分布模型。从图中给出的参数条件可以看出，威布尔分布与海杂波的幅度分布拟合得最好，其次是对数正态分布。事实上，对于不同条件，杂波分布特性不同，图中只针对所示条件下的杂波进行分析。

图36 不同参数下杂波分布的最佳模型Fig.36 Best model for clutter distribution with different parameters

图37为X波段3°擦地角，高海情(15 m/s)，顺风，HH极化下的散射系数时间序列和与之相对应的均值归一化幅值时间序列。从图37(b)的杂波概率分布函数(Probability Distribution Function,PDF)中可以看出，在高情下(风速为15 m/s时)，只有K分布能很好地拟合海杂波的幅度分布的拖尾部分，其他分布拟合较差。

图37 3°擦地角U10=15 m/s HH极化顺风散射系数时间序列及均值归一化杂波幅值Fig.37 Time series of scattering coefficients and normalized clutter for HH polarization under U10=15 m/s and 3° grazing angle

表8给出了U10=10 m/s，X波段(10 GHz)和Ku波段(15 GHz)下，入射角分别为30°,45°,60°,80°时HH极化和VV极化的散射回波序列的统计分布情况，在表中，各分布的名称都用其英文缩写表示。由表8可以得出结论，在X波段(10 GHz)和Ku波段(15 GHz)，小入射角海杂波分布符合威布尔分布，在入射角为45°和60°时，HH极化海杂波的统计分布符合威布尔分布，VV极化海杂波的统计分布则更符合K分布，而在大入射角时，海杂波的分散效应更强，局部散射成分和散射机理更加复杂，此时威布尔分布与K分布也都退化为瑞利分布，这时的海杂波统计分布也更符合瑞利分布。

表8 U10=10 m/s不同条件下海杂波幅度最佳拟合模型统计分布Tab.8 Best-fit model statistics distribution for sea clutter amplitude at U10=10 m/s

图38给出了不同风速下的动态海面电磁散射杂波的多普勒谱。可以看到，多普勒谱的宽度会随着风速而变化，风速越大，谱越宽。因为风速越大，海面越粗糙，不同频率成分的海浪越多，多普勒就会出现频谱展宽效应。

图38 入射波频率为1.5 GHz时不同风速后向散射场的多普勒谱Fig.38 Doppler spectra of the backscattered field at different wind speeds for an incident wave frequency of 1.5 GHz

与时变海面回波仿真类似，时变海面及目标回波特性仿真也存在着海面状况复杂，仿真计算量大的问题，还需要考虑到目标自身的几何结构和材质的复杂性，同时，对于动态条件下，目标的运动及目标与海面的复杂耦合作用也需给予考虑。这对建模算法本身和算法的计算效率进一步提出了更高要求。Burkholder等人[151]采用谱加速的广义前后向方法对二维时变海面与目标复合场景的动态回波进行仿真。复旦大学金亚秋和刘鹏等人[56]采用FEM-DDM方法研究分析了动态海面与其上方飞行目标的动态回波特性，其中采用区域分解技术提高求解效率。电子科技大学赵志钦等人[152,153]采用数值方法开展了对三维海面、三维动态破波模型以及三维动态海面与目标复合电磁散射回波的多普勒回波频谱研究。西安电子科技大学张民、陈珲等人[87,154,155]研究了三维动态海面及其上方电大尺寸舰船目标的电磁散射回波和多普勒频谱，分析了舰船六自由度运动对回波和散射的影响。北京航空航天大学李晓飞和许小剑[156]通过2阶小斜率(Small Slope Approximation,SSA) 近似方法研究了三维动态海面的雷达回波谱，同时开展了海面上方运动舰船的雷达回波研究。西安电子科技大学丁慧芬、郭立新等人[150,157]提出了一种基于面元散射模型的电磁散射建模混合方法，研究了复杂海背景下掠海低飞目标的电磁散射特性和多普勒谱多径效应，如图39所示。图39(a)中的仿真参数为：电磁波入射频率为10 GHz，入射角为θi=45°,φi=0°，目标位于海面上方5 m位置，目标飞行速度为100 m/s，海面风速为3 m/s，风向φw=0°，海面大小为128 m×128 m。图39(b)中仿真时长为T=5 s，时间采样间隔为0.005 s。其他仿真参数与图39(a)相同，仿真结果为该场景下的回波多普勒谱。图39(c)给出了同场景，风速为10 m/s时的回波多普勒谱。从图39(a)可以看出，在镜像散射方向上，海面散射占主导地位。在后向方向上，复合散射主要由目标散射和耦合散射贡献。从图39(b)可以看出，目标-多径散射回波的多普勒谱峰出现了较大频移，峰值位置主要对应着目标运动产生的多普勒的峰值，对比图39(b)和图39(c)可以看出，随着风速的增大，目标多径多普勒谱会有多个尖峰，使得多普勒谱宽展宽。多个多普勒谱尖峰是目标与局部海面面元耦合散射产生的镜像散射单元相对于入射源有不同的多普勒频移导致的，海况越高多径多普勒尖峰也就越多，导致的多普勒谱展宽也就越多。

图39 复杂海背景下掠海低飞目标的双站RCS和归一化多普勒谱Fig.39 Bistatic RCS and normalized Doppler spectrum of a low-flying target in a complex sea background

实际雷达探测中，传感器通常对动态海面进行持续探测，发出等间隔的时间脉冲，在仿真得到回波特性后，对不同慢时间下得到的回波进行脉冲压缩，即可得到脉压后的杂波分布。本算例中雷达发射脉冲间隔为0.025 s，一共发射604个脉冲，总时长约15.1 s。图40为阿利伯克级舰船与动态海面脉压后的杂波分布图，归一化杂波概率分布对数值，和不同距离单元回波的时间相关性。仿真参数为：雷达俯仰角为89.8°，中心频率35.05 GHz，带宽100 MHz，海面大小为400 m×400 m，雷达入射方位角为0°。仿真模型中，舰船在-50～50 m区间内，因此在这一区间的分辨单元中可以看到明显的回波，其他分辨单元为海面回波，因为舰船较海面回波非常强，故海面单元回波不明显。图40(b)中，为了清晰显示在不同杂波幅度的概率分布，将每个区间杂波概率取对数，因为复合场景中包含舰船，引起强散射，与海面回波散射幅值差距较大，所以概率分布函数取值主要集中在两个区间，分别代表舰船散射(杂波幅度较大区域)和海面面片散射(杂波幅度较小区域)。从时间相关性可以看出，在舰船的区间内，杂波相关时间非常长，而在海面单元内，时间相关性迅速衰减。

图40 复杂舰船与海面的杂波分布图、杂波概率密度分布、时间相关性Fig.40 Complex ship and sea clutter map,clutter probability distributions and time correlation

在高海情下，由于海上波浪的破碎，在杂波中表现为回波出现大值，并且会持续一段时间，这被称为“海尖峰”，尤其在高分辨雷达小擦地角观测下，这种现象更为明显。而且与一般海面不同，“海尖峰”通常体现出HH极化大于VV极化的特征。如Kalmykov等人[158]对海面小擦地角电磁散射观测中发现了极化特征的变化即小擦地角下HH大于VV极化结果的现象，这种现象称为“超现象(Super Event)”。海上波浪破碎与海尖峰现象的关联性在众多的实际观测数据和仿真研究上得到了证实，如美国海军实验室高分辨雷达的对海观测中也发现了远大于杂波均值，且持续时间较长的“海尖峰”出现在时间序列中，研究人员都将海尖峰现象与海面上的波浪卷曲破碎现象进行了关联[159-163]。Liu等人[164]通过将HH和VV极化下的电磁散射成像结果和实际海面的录像进行对比，发现“海尖峰”这种非布拉格散射的超现象与波浪破碎现象密切相关，并确定了破碎波是产生海尖峰现象的主要原因。由于海尖峰在回波特征上与目标回波非常相似，极易出现目标误判，引起虚警。因此深入分析海尖峰现象并通过仿真解释海尖峰出现的物理机理，区分海尖峰与目标的散射特性，才能为海上雷达目标检测提供理论支持。Kwoh等人[165]采用几何绕射理论计算了波冠劈结构散射，结合微扰法计算了破碎浪张力波散射分量；在针对破碎波散射特性仿真研究中，Holliday等人[166,167]基于LONGTANK破碎波模型，利用前后向迭代矩量法分别计算了不同几何形态的破碎波的散射。电子科技大学赵志钦等人[143]将二维LONGTANK卷浪模型中不同时刻的卷浪进行拼接，生成了三维破碎波，并使用多层快速多极子计算三维破碎波的散射特性。张民等人[144]利用曲面劈模型模拟中等尺度的破碎浪，并利用相位修正的双尺度法计算海面散射场。北京理工大学吴比翼等人[168]通过求解非线性水动力方程，数值模拟了深水中典型倾伏破碎波的发展过程。同时，利用二维有限元方法模拟了不同极化条件下不同时间的破波散射。西安电子科技大学李文龙[169]基于简单的数学函数建立了一维时变卷浪模型，在此基础上应用矩量法研究了一维时变卷浪的后向电磁散射；孟肖[170]还基于LONGTANK模型延拓出三维破碎浪模型，并研究了含卷浪的三维局部海面模型，并利用IEM计算含卷浪的粗糙海面总体后向散射场分布；该团队的郭立新、魏仪文等人[103,171]提出了用有限大二面角劈结构近似模拟溢出型碎浪，并利用相位修正的双尺度法计算小擦地角入射下含破碎波海面的散射时间序列，同时仿真模拟了不同频段下的多普勒谱，图41给出了X波段下的多普勒谱，入射频率分别为f=10.0 GHz，入射角θi=75°，每个分辨单元的尺寸为 20 m×20 m，风速为U=10 m/s。时间采样点为Nt=8192，时间采样间隔为Δt=0.005 s，取50个粗糙面平均。从图41可以看出含与不含破碎波的海面相比，含破碎波海面的多普勒谱中出现了一个新的峰值，并且多普勒中心频率向更高的频率发生了频移，同时多普勒谱也发生了展宽，这些现象都是由波浪破碎引起的，因为破碎波无论在速度上还是能量上，都较为明显地区别于海面背景；破碎波引起的多普勒谱上的变化在HH极化下更加明显，由于HH极化下“海尖峰”更明显，破碎波的非布拉格散射更突出，因此散射结果、回波特性、“海尖峰”现象以及多普勒谱，都是HH极化下影响更明显；

图41 X波段下杂波多普勒谱(f=10 GHz)Fig.41 Doppler spectrum at X-band (f=10 GHz)

图42给出了破碎波对HH/VV极化比的影响。图42(a)、图42(b)分别给出了含破碎波和不含破碎波的时变海面回波HH/VV极化比。可以看出，在图42(a)中，|Ehh|/|Evv|在很多区域都大于1，说明HH极化下电场强度经常会出现大于VV极化电场强度的情况，这正是“海尖峰”现象的特征，在|Ehh|/|Evv|大于1的时间区域中，正是由破碎波从这一雷达分辨单元中经过。而图42(b)中，虽然也有|Ehh|/|Evv|的值大于1的情况，但总体来说，比值并不是很大，且持续时间非常短，会马上消失，这说明这些偶然性的|Ehh|/|Evv|的情况只是由于海面的随机波动引起的，是一种偶然现象。

图42 HH极化与VV极化下电场幅度比值的时间序列Fig.42 Time series of electric field amplitude ratios under HH polarization and VV polarization

图43给出了含多卷浪海面与目标复合的多普勒谱。仿真参数为：f=10 GHz,U=5 m/s,θi=75°,φi=-90°，极化方式为H H 极化，海面尺寸为100 m×100 m，目标静止。从图中可以看出，纯目标散射只有唯一的多普勒谱峰，谱峰的位置在多普勒中心没有产生频移，这是因为目标是静止的。而海浪-导弹的多普勒谱相对纯目标有所展宽，并且出现了多个多普勒谱峰尖，多普勒谱峰尖是目标与局部海面面元、卷浪与其周围局部海面面源耦合散射产生的镜像散射单元相对于入射源有不同的多普勒频移导致的。

图43 含多卷浪海面与目标复合多普勒谱Fig.43 Composite Doppler spectrum of surface and target with multi breaking waves

1.3 基于数值仿真的复杂海面及目标SAR成像研究

随着成像技术的发展，能直观体现海面纹理及目标几何特征的SAR图像越来越受到青睐，相较于电磁散射的RCS及回波特性，SAR图像更加直观，也能体现海浪波的细节变化以及海面上的其他特征信息。对复杂海背景与目标复合的雷达回波特性及SAR成像仿真研究逐渐成为国内外学者研究的热点问题之一。海面的SAR成像模型最早是由Alpers[172]提出的用来分析沿方位向传播的海杂波的SAR成像特征的速度聚束(Velocity Bunching,VB)成像模型，解释了倾斜调制、流体力学调制和速度聚束调制对海面SAR图像的调制作用。根据速度聚束理论。由于合成孔径雷达成像需要成像时间的积累，在积累时间内，海面的运动也会引起SAR图像成像模糊，但上述模型对海面速度的调制只能在成像时间较短时起到作用。在此基础上，Alpers[172]基于蒙特卡罗方法研究了海杂波与SAR图像光谱之间的关系。Plant[173]证明了Lyzenga (1983)[174],Kasilingam(1988)等的“时间依赖”理论以及Brüning(1991)等的“速度聚束”理论对于短时间积分是相同的，但对于长时间积分下的聚焦问题上是不同的，并得出了在短时间积分内，海浪的相速度起着次要的、几乎可以忽略的作用，但随着积分时间的增加，相速度占主导作用的结论。Vachon等人[175]利用RADARSAT实测结果对海面SAR成像仿真结果作了验证，提出了CCRS/RADARSAT成像模型。此外，Hasselmann等人[176]提出了分布式面元SAR成像模型，此模型在每个雷达慢时间对海面场景进行模拟，根据雷达参数对SAR回波进行仿真。Hasselmann等人[176]在前面学者的研究基础上，对已有的海面SAR成像机理进行了总结分析形成了较为完整的海杂波的成像理论。国内，国家海洋二所的杨劲松等人[177]、黄韦艮等人[178]等通过仿真模拟研究浅海地形的SAR成像特性，为海底地形的反演提供了良好的理论基础。中国科学院遥感应用研究所的黄晓霞等人[179]讨论并分析各种成产型的海洋表面膜特征及其在海洋SAR图像中影像特征，对渤海湾的SAR图像中的表面膜特征进行检测并对这些表面膜特征成因进行了分类。北京航空航天大学的许小剑等人[180-182]分别从时域和频域两个方面研究了海面的SAR回波仿真算法。复旦大学的金亚秋等人[183]研究了海面双站散射的SAR成像算法。西安电子科技大学张民等人[184,185]研究了基于扩展非线性chirp scaling算法的海面双基地SAR图像和基于四路径模型的复合船-海场景双基地SAR图像；电子科技大学赵志钦和聂在平等人[186]利用双尺度海面模型基于PM海谱进行海面模拟，研究大尺度长波和小尺度短波对海面SAR成像的影响。复旦大学徐丰等人[187]利用深度卷积网络从SAR图像中自动学习多层的特征表征，再利用学习到的特征进行目标检测与目标分类。南京理工大学丁大志等人[188]基于弹跳射线法，在Faster RCNN目标检测网络的基础上，根据真实舰船目标的尺寸改变候选框的初始尺寸以及利用特征融合的方式对原算法架构加以改进，进一步提高了算法对SAR图像舰船目标检测和识别的能力。西安电子科技大学郭立新、董春雷等人[189-192]基于SBR方法仿真模拟了典型目标的SAR图像及复杂地面与目标复合的SAR图像，并基于SBR与小斜率近似方法结合仿真模拟了复杂海面与掠海飞行目标复合模型的SAR图像。图44对比了在不同风速海况下SAR掠海巡航导弹目标的SAR成像特性。目标高度距离海面5 m。图44(a)与图44(b)仿真中所对应的风速海况分别是U10=3 m/s和U10=10 m/s。雷达的工作频率为10 GHz，入射角为45°，目标高度为10 m，海面上方风速为U10=5 m/s，风向为45°和135°，距离和方位分辨率为0.15 m，颜色条反映了SAR图像的强弱。可以看出，在不同风速海况时海面SAR图像的纹理及多径散射形成的目标镜像的成像都出现了较大不同。首先目标高度下降，目标强散射点与海面多径散射造成的SAR成像强度明显增强，同时可以看出由于遮挡效应形成的阴影区位置以及镜像位置发生变化，更加靠近目标图像位置。而在U10=3 m/s，风速海况较低时，由于海面风浪起伏较弱，以毛细波散射为主，这时的海面成像结果也可以反映毛细波的起伏纹理。当U10=10 m/s时，海面上多尺度结构散射形成了SAR图像的纹理也可以反映海面的起伏特性，图像的大尺度纹理反映了海面的大尺度波浪起伏，而在高海况时海面局部碎浪和泡沫结构增强了局部海面图像的强度。而且这时镜像的扩散效应比较明显，这是由于此时的局部海面的倾斜效应较强，但是由于与局部海面特殊结构存在导致散射增强，局部多径耦合散射效应也相应增强，导致镜像图像强度增强。

图44 不同海况下掠海巡航导弹目标SAR图像Fig.44 SAR images of missile targets at different sea states

图45和图46为距离多普勒方法仿真得到的海面上方航母舰船编队的SAR图像。脉冲信号宽度为1 ms，信号载频为f0=10 GHz，带宽150 MHz，机载平台飞行高度h=10000 m，飞行速度为100 m/s，脉冲重复频率为200 Hz，合成孔径时间10 s，仿真成像区域大小为1200 m×1200 m。海上风速分别取0.5 m/s,1.0 m/s,3.0 m/s。图47分别给出了不同风速下，采用深度神经网络对目标进行识别的结果。

图45 不同海况舰船编队SAR图像θi=45o,φi=45oFig.45 SAR images of ship formations in different sea states at θi=45o,φi=45o

图46 不同海况舰船编队SAR图像θi=45o,φi=90oFig.46 SAR images of ship formations in different sea states at θi=45o,φi=90o

图47 不同海况下SAR图像中目标识别结果Fig.47 Target recognition results in SAR images under different sea states

2 复杂海面及目标散射特性研究展望

目前，国内外学者已在复杂海面及目标散射特性及回波仿真研究方面形成了一系列成果，散射算法及其加速技术已经趋于成熟。但这些成果如何对实际战场中目标探测和检测进行支持仍需进行大量的工作，复杂动态海面与目标复合散射及回波仿真的意义体现在如下方面：

(1) 弥补实测数据物理意义缺乏，实测数据结果与表征参数关联度不高的问题：实际工程中复杂海环境下目标检测和识别通常是基于大数据驱动，忽视了雷达回波或者SAR图像的物理特性，纯数据驱动算法天然忽略了物理机理，其预测结果缺乏可解释性，而基于仿真的回波数据，其仿真过程完全基于具体物理过程，仿真结果物理意义明确，与表征参数(包括海洋环境参数、目标参数、雷达平台参数)直接相关，可解释散射随各种参数变化规律的物理机理和散射背后的物理意义。

(2) 经过校验的仿真数据可为人工智能识别算法提供有效训练数据：实际情况中，对于非合作目标，很难获取足够的不同参数下的数据作为训练数据成为人工智能识别算法的学习依据，准确的检测器和目标识别算法的设计都需要建立在大量不同情况下的海量数据之上，而准确的基于物理机理的电磁散射仿真可以认为是一种低成本且可靠的数据增广方式，可为人工智能识别算法提供有效训练数据。

基于以上分析和梳理，我们总结出未来复杂海洋环境与目标回波仿真及探测中面临的问题，并给出一些后续研究方向和建议：

(1) 仿真结果与实测数据进行校验的指标评价体系研究和建立：仿真结果要想作为实验数据的补充数据集，需要满足与实测数据对比的精度，即满足一定的置信度，否则仿真结果训练的网络用于实测数据中的目标检测和识别必然会面临网络泛化问题。现有算法在计算粗糙面与目标复合散射问题时，通常对算法的验证都是将仿真结果与实测结果进行RCS的比对，以均方根误差在某一dB值之内，即可认为正确。而实际杂波仿真时，回波多普勒谱、杂波数据、幅度分布、时间及空间相关性等特征其实对目标检测与识别可能具备更大的意义，而RCS在一些区间的数值即便不是“绝对精确”，对判别结果也影响并不大。因此，如何论证散射数据潜在数据特征，建立指标体系和评价体系，建立置信度评估模型是理论仿真需要解决的一大问题。

(2) 综合考虑海上电磁波传播与散射的电磁仿真模型研究：实际对海环境目标探测中，由于海面上方存在不均匀的盐雾、水凝气等复杂因素，会导致电磁波存在衰减和传播路径的变化，例如海上通常存在蒸发波导，会引起海上电磁波反常传播效应，电磁波首先经过波导到达目标后再散射，又例如天波超视距目标探测中，也要考虑电离层对电磁波的反射引起的电磁波相位、传播方向及极化的影响。大多数文献中，学者在考虑散射问题时，只是将雷达波认为是平面波或者波束传播，没有考虑传播路径引起的损耗、衰减、方向及相位变化对散射的影响。而在实际工程问题中，这些因素都严重影响着目标探测及定位的精确度，因此需要更深入地对传播和散射问题进行统一建模，使其更符合实际探测需求，保证数值仿真和实际测量的环境一致性。

(3) 融合物理机理的目标检测和识别方法研究：随着机器学习模型复杂度的日益增加，深度学习模型对数据的认知并进行决策的过程更类似“黑匣子”，对于目前常用的机器学习方法，直观上人们已经无法去理解机器如何做出决策。但是在军事领域，尤其是在雷达目标检测领域，错误的决策通常会引起较为严重的后果，因此决策的错误需要有可追溯性和可解释性，也就是人们不仅需要知道判别结果，还需要了解决策是如何做出来的，模型的可解释技术主要是对输入的各个特征进行定量评价，找到对结果影响最大的特征。或者进行进一步分析，考察特征的相关性。因此对于回波信号的解译中，如何建立融合物理模型和深度神经网络的检测与识别算法也是当今的研究热点之一。

(4) 加强对海杂波实测研究与理论研究融合。虽然国内多家单位开展了造波池、实际地物、实际海面等背景中目标电磁散射测量实验，但所测量的背景、目标种类均有限，且目标为简单目标或缩比模型，无法满足实际工程需求。因此需要构建实际复杂战场环境进行测量和仿真，一方面积累足够测量数据，一方面可以对仿真模型在不同场景下的稳定性和精度进行验证，结合实际工程模型，对仿真算法进行精度修正。使得仿真算法具备不同场景下的普适性。