在高中数学解题教学中让学生学会反思质疑*

武瑞雪

反思是指思考过去的事情，从中总结经验教训；质疑是指提出疑问，既包含提出不会、不懂的问题，也包含因怀疑去发现、提出新问题。批判性思维是指通过一定的标准评价思维，进而改善思维。批判性思维不是否定性思维，它是一种具有创造性和建设性的思维。反思质疑能力是个体发展批判性思维的基础，是创新型人才的必备能力。

学生擅于反思质疑，才能“去伪存真”，在“定论”中发现新问题，才能批判性地接受新知识、新技能，开启创新的大门，才能满足社会发展、科技进步的需要。《普通高中数学课程标准（2017年版2020年修订）》（以下简称《新课标》）在“课程目标”中指出“树立敢于质疑、善于思考、严谨求实的科学精神”，在“教学建议”中指出“教师要加强学习方法指导，帮助学生养成良好的数学学习习惯，敢于质疑、善于思考，理解概念、把握本质”。可见，教育目标或使命的要求之一就是培养善于独立思考、敢于质疑的批判性思维者。

一、一题多法，让学生反思解法优劣

美国数学家G.波利亚在《怎样解题》一书中指出“没有任何一道题是可以解决得十全十美的，总剩下些工作要做，经过充分的探讨总结，总会有点滴发现，总能改进这个解答，而且在任何情况下，我们总能提高自己对这个解答的理解水平”。［1］这里所说的“剩下些工作”，就是解题后的反思。在高中数学解题教学中，教师应该积极引导学生进行反思，反思是否出错，是否有更简捷解法，以及一题多法中各解法的优劣。

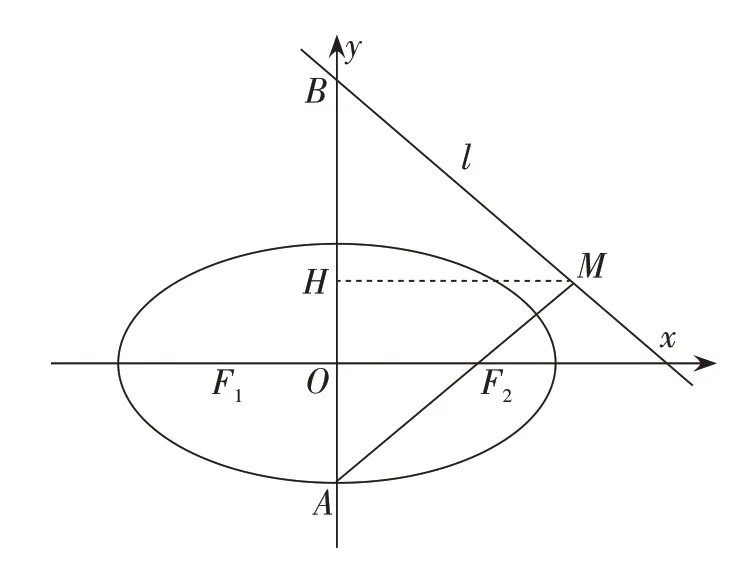
（图1）

点评：此法属于常规解法，但运算量大，过程烦琐。

【设计意图】（1）从上述三种思路的繁简程度看，仔细审题，选择简便的方法很重要。（2）进行解题教学时，上述各解法不能由教师直接给出，而应由学生课前先做，然后教师批改。教师在充分了解学情后，汇总各种解法，包括典型的错误解法，也包括教师预设而学生没有想到的解法。（3）课堂上，教师可将上述各解法通过展台展示，或由学生板演于黑板，并留给学生充足的思考、比较的时间，让学生在反思、质疑中搞清楚各种解法的优劣。（4）“一题多法”教学可培养学生多角度观察问题、探索解法的习惯，让学生在繁简之间进行对比、分析和判断，还能让学生学会批判性地接受别人的解法、优化自己的解法。教师经常性地进行“一题多法”教学和解后反思、质疑训练，可有效促使学生发展批判性思维。

二、故意示错，让学生养成反思质疑习惯

在教学中，教师可根据已有的教学经验和学生以往常犯的错误，预估学生可能出现的错误，故意“挖陷阱”，向学生展示错误的解题过程，给学生制造认知困境，创造让学生反思质疑的机会，让学生养成反思质疑的习惯。

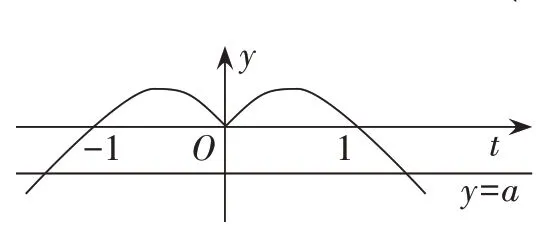
（图2）

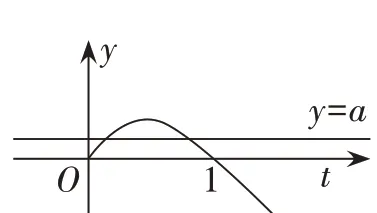
（图3）

【设计意图】（1）教师展示学生的错解后，应给学生足够的反思质疑时间，教师一定要耐住性子，等待学生找出错因。（2）教师不能因为学生质疑错误而指责学生，要切实保护学生质疑的积极性，努力营造和谐融洽的质疑氛围，让学生敢质疑、乐质疑，在不知不觉中成长为批判性思维者。

三、开设专题课，让学生自纠、互纠

教学实践证明，将一道错题的错解原因彻底搞清，要比做一道甚至多道新题更加有效。［2］开设“易错题”专题课，系统性地教学易错知识点，能有效加强学生对知识点的记忆，培养学生日后遇到同类型问题时举一反三的能力，有利于将学生培养成批判性思维者。例如，在高三复习时不妨将案例3、案例4 这两道易错题选作“等价转化思想”专题课的教学案例，集中纠错、点评。

案 例3：已 知a，b∈R，ab＞0 函 数f( )x=ax2+b(x∈R)。若f（s-t），f（s），f（s+t）成等比数列，则平面上点（s，t）的轨迹是（ ）。

A.椭圆 B.双曲线

C.直线和椭圆 D.直线和双曲线

要解答此题，首先利用等比数列得到等式，然后对其进行恒等变形即可确定其轨迹方程。

生7（错解）：由题意f（s-t）f（s+t）=［f（s）］2，代

点评：此题考查等价转化思想、轨迹方程求法、逻辑推理与数学运算素养，关键是等价转化。

要解答此题，如图4，设B（x1，y1），C（x2，y2），求出直线AB、AC的方程后可得M、N的横坐标，从而可得PM+PN，联立直线BC的方程和椭圆的方程，结合韦达定理化简PM+PN，从而可求k的范围，同时要注意判别式的要求。

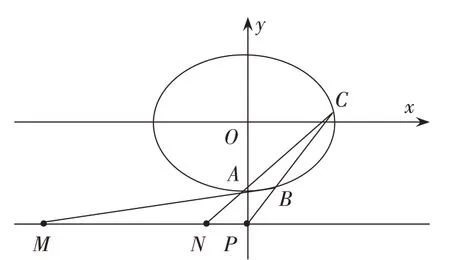
（图4）

【设计意图】（1）生9 思路很常规，仅因忽视隐含条件Δ＞0而致错，实属可惜。（2）对于来自学生的典型错误解法，一定要让学生先自纠，不能自纠时，再让同学之间互纠。（3）教师一定要留给学生足够的时间来交流、辩论、质疑，让学生自由地表达意见、异见。（4）对于因反思而提出质疑的学生，无论质疑是否合理，都应表扬鼓励，确保学生只要自学或听课时有疑问和困惑，就敢于质疑，让学生真正体会到反思质疑的乐趣。

四、重视对数学错题集的整理与利用

在学习高中数学时，除了要让学生记住上面案例中提及的“用换元法时，一定要注意新元范围”“进行转化时，一定要等价”“直线与二次曲线交于不同两点，勿忘判别式Δ＞0”之外，还应让学生适时在错题集上分门别类记录如下易错、易混知识点，并经常翻阅，这对培养学生反思质疑能力，促其成长为批判性思维者，可起事半功倍的作用。

（一）集合类

（二）函数类

在解函数类问题时，一定要注意以下“形似而神不同”的问题。

“若函数f(x)=x2-ax+1在（-∞，2）上为减函数，求实数a的取值范围”与“若函数f(x)=x2-ax+1 的递减区间为（-∞，2），求实数a的取值范围”。两题答案分别是［4，+∞）、{4}。

“已知函数y=lg(x2+mx-m)的定义域是R，求实数m的取值范围”与“若函数y=lg(x2+mxm)的值域为R，求实数m的范围”。答案分别为：{m|-4 ＜m＜0}、{m|m≤-4或m≥0}。

（三）数列类

提升学生反思质疑能力，发展其批判性思维的教学策略还有很多，如，夯实学生对基础知识、基本思想方法的掌握，为其反思质疑奠定坚实基础；建立平等的师生关系，让学生敢于表达个人见解，勇于质疑教师、教材、教辅书、专业杂志等权威；让学生养成预习习惯，学会反思、质疑、批判式阅读，自主参与新知识的建构过程，学会对新概念、定理、法则中的不理解之处独立思考并提出质疑、批判；在导学案中设计一些易引起歧义的问题，让学生生疑、质疑，然后释疑；重视变式题教学，让学生从不同解题情境中发现不变的本质和解题规律；教师以身作则，树立善于反思质疑的榜样，并教会学生反思质疑方法；等等。

作为一线数学教师，我们有义务思考、探讨如何创设以问题为核心的反思、质疑的教育教学环境，让我们的学生会反思、善质疑，顺利成长为善用批判性思维的人。