采用SIMT结构GPU的二维离散哈尔小波变换的优化

李一芒，孙凤全

(常州大学 机械工程学院，江苏 常州 213000)

0 引言

与傅里叶变换相比，小波变换能够通过低通滤波器和高通滤波器将图像的基本信息与变化信息、边缘信息分离开来，并且由于小波变换具有紧支撑的性质，即取值在某一区间内为常数，在此区间外为0，使得能量较为集中，能够反映局部信息的变换，因此被应用于图像处理领域。作者在研究夜间图像检测过程中，将小波变换应用于图像融合，根据选择小波变换的四项原则，即正交、线性相位、连续、紧支撑[1]，选择了二维离散哈尔小波变换，但是在CPU环境下运行需要耗费大量资源，实时性存在问题，为方便后续研究，本文对GPU环境下的二维离散哈尔小波变换进行了研究。

GPU(graphic processing unit)最初是一种图形处理器，后来根据人们的需要被用作并行计算的处理器，对于GPU下的小波变换已有许多，例如文献[2]在伪代码层面添加滑动窗口机制处理大数据流；文献[3]将数据进行全局划分，实现小波变换；文献[4]通过改写寄存器文件结构，提升SIMD结构数据处理速度；文献[5]将MPI技术和GPU结合；文献[6]将数据分成奇数块和偶数块进行处理；文献[7]基于晶格结构提出了新的离散小波算法。本文采用了一种正在发展中的新架构SIMT(单指令多线程)，在它本身配套的CUDA C算法平台上进行实现，将二维离散小波变换对应到线程，进行并行公式推导，并且通过调整GPU的逻辑布局、同步设置、内存优化，实现性能的提升，比SIMD架构GPU效率可提升16.3%，比CPU效率可提升51.1%。

1 相关理论基础

计算机架构根据指令和数据进入CPU的方式分为单指令单数据(SISD)、单指令多数据(SIMD)、多指令单数据(MISD)、多指令多数据(MIMD)，其中SIMD、MIMD以及后来出现的SIMT就是GPU中的数据并行结构体系[8]。SIMT架构的概念最早由NVIDIA公司在2008年于文献[9]中提出，SIMD架构是传统的数据并行结构，区别如图1所示。

图1 SIMT架构与SIMD架构图

如图1(右)所示，在SIMD结构中，数据被打包成一个向量，具体的数量取决于有多少个SP(流处理器)，这就是GPU处理大量数据快的原因，也是并行计算[10]的基础。但是并不是所有数据都适合向量化，为了追求速度，着色程序越来越长，并且因为向量化所产生的代码量巨大，需要类似于内存对齐[11]这样的操作，对编译器的负荷巨大。

如图1(左)所示，区别于SIMD结构GPU的是，在SIMT结构GPU中，多了线程的概念。将一个数据就存放在一个线程内，也就有了对应的地址，这样就可以对单个数据进行操作，为了满足并行的要求，SIMT将32个线程组合成一个线程束[12]。一个线程束里的数据同时只能响应一个命令，如果其中部分线程需要响应其他命令，那么这部分线程进入非活跃状态，等活跃线程执行完再执行。这样的执行方式从某方面来讲和SIMD结构GPU将数据向量化存在相似[13]，因此SIMT结构是在SIMD的结构基础上设计出来的。

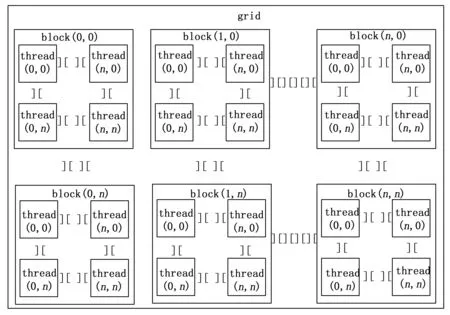
图2 GPU逻辑架构

SIMT结构对比SIMD结构的优势在于不需要考虑数据向量化、内存对齐的事情，并且它最小并行的数据宽度为32，远小于SIMD，所以它对于数据的处理更加高效且灵活，同时，指令和数据的调度编译[14]工作更加简单。在本文的实验中，SIMT架构的GPU比SIMD架构的GPU快上19.5%。

2 SIMT结构下的小波变换

2.1 SIMT结构GPU的逻辑架构

SIMT结构以线程为基础，统一的存在一个网格(grid)内，网格内包含若干线程块(block)，线程块内包含若干线程(thread)，每个线程都有一个输入数据，这些线程会被分配相对应索引号，通过索引号可以操纵数据，GPU会根据网格和线程块的维度分配相应维度坐标，类似于矩阵坐标。

网格的维度和线程块的维度是由我们自行指定的，可从一维设置到三维，这里以二维结构来设置一个矩阵为例，则逻辑结构如图2所示。

2.2 二维离散小波变换的并行公式推导

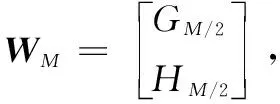
设图像矩阵A中的元素为ai,j，βi,j、γi,j、δi,j、ζi,j分别为矩阵C、D、E、F的元素，则经过推导可得：

(1)

(2)

(3)

(4)

接下来根据式(1)～(4)将数据分配进线程。根据图(2)可知,线程块ID以列优先的方式分配，线程的ID以块为单位，在每个块中再按列优先分配ID，线程ID在其所在的块内为独有。矩阵的数据存储进线程的时候不按块为单位，根据全局的线程按照列优先进行存储。设图像矩阵AM×N中的元素为ai,j，线程矩阵中的元素为μi,j，BH×I的线程块矩阵中的元素为νi,j，则推导可得：

ai=μi+H·νi

(5)

aj=μj+I·νj

(6)

在实际存储形式中，数据按照一维数组的形式进行存储，GPU在访问全局内存[16]的时候也是直接访问数据的全局内存索引，因此需要找到全局内存索引和矩阵坐标的关系，在这里要注意的是和矩阵数据存储原则不同，全局内存索引的分配按照行优先原则而并非是列优先原则。设全局内存索引为S，根据式(5)、式(6)可推得全局内存索引和矩阵元素关系为：

S=ai+aj·M

(7)

首先按行方向对图像矩阵的列进行变换，需要知道数据取出位置和数据存储位置。设变换后数据取出位置的全局内存索引为SO1，SO2，根据式(7)可推得：

SO1=2ai+aj·M

(8)

SO2=2ai+aj·M+1

(9)

而数据的存储位置由于式(8)、式(9)推导过程中为了先对应均值块，使得有些索引超出了界限，而如果均值块处理后的数据存储位置索引按行方向只取前M/2个索引，而细节块处理的数据存储位置的索引由均值数据索引向右M/2个偏移量则可解决。设变换后数据存储位置的全局内存索引为SI1，SI2则可推得：

SI1=S=ai+aj·M

(10)

SI2=ai+aj·M+M/2

(11)

其次按列方向对图像矩阵的行进行变换，和列变换存储位置相似，均值块处理后的数据存储位置索引按列方向只取前N/2个索引，细节块处理的数据存储位置索引由均值数据索引向右偏移M2/2个偏移量[17]。设变换后数据取出位置的全局内存索引为SO1，SO2，数据存储位置的全局内存索引为SI1，SI2，则可推得：

SO1=2aj·M+ai

(12)

SO2=(2aj+1)·M+ai

(13)

SI1=S=ai+aj·M

(14)

SI2=S=ai+aj·M+M2/2

(15)

至此，完成了二维离散哈尔小波变换的并行公式推导。

3 GPU的进一步优化

3.1 更改寻址方式

由于在运行一个进程的时候，所需要的内存大小其实会超过实际的内存[18]大小，因此会通过分页的方式，整合计算机的存储资源，映射出一个超过物理内存大小的虚拟内存[19]，需要数据的时候通过页和页帧将数据调度进物理内存中进行操作。CPU与GPU传输数据也需要用到虚拟内存，其关系流程如图3所示。

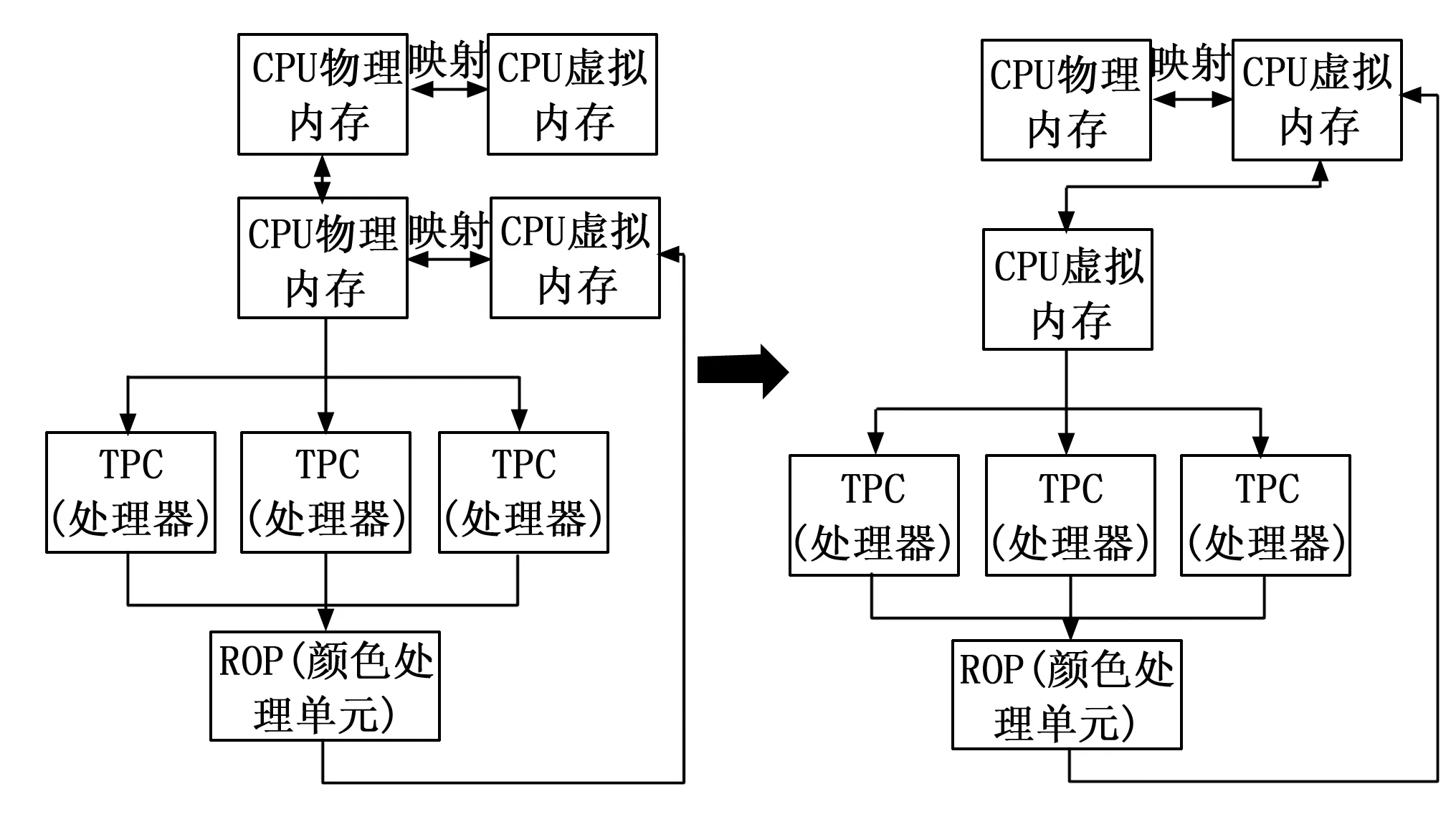
图3 GPU与CPU数据流通流程图

如图3左所示，数据逻辑上存放于虚拟内存，通过虚拟地址将数据调度进入CPU的物理内存中，CPU和GPU的物理内存通过总线互联传递数据，GPU再将数据存放于GPU的虚拟内存中，等到使用的时候进行调度，送入TPC(处理器)[20]中进行处理，经过ROP(颜色处理单元)输出结果到GPU虚拟内存中，需要被传输的数据通过虚拟地址将数据调度进GPU物理内存，传输给CPU物理内存，再将数据存放进CPU虚拟内存中[21]。

这种模式会产生一些不必要的开销，可以看到在这过程中数据在被不停的复制、映射，而这些是由于寻址方式造成的，因为host端与device端开辟的空间地址不统一，互相不能直接进行数据的存取，所以本文在这里采用虚拟内存统一寻址的方式，使得GPU虚拟内存和CPU虚拟内存的虚拟地址统一，此时GPU就可以直接从CPU的物理内存中取用数据了，简化了代码，减少了不必要开销，便于后续处理。

3.2 调整逻辑布局

要找到能够处理大分辨率数据速度最快的逻辑布局，就必须从数据在SIMT结构GPU中被处理的底层逻辑上去寻找，否则每一个逻辑布局都去尝试根本就是无法做到的。数据的存储在实际的硬件中是以一维的方式存储的，但是SM(流式多处理器)处理数据的最小执行单元并不是线程，在数据处理的过程中，线程束才是SM中基本的执行单元。当一个内核被启动时，网格块中的线程块会被分配到某一个SM上，这些线程块里的线程就会分成多个线程束，在一个线程束中，所有被分配到线程上的数据都会执行这一个线程束被分配到的指令，目前每个线程数是以32个线程为一组的，一个线程束就能够同时对32个数据执行同一个命令，而在命令分配的时候，多个线程束会分配到同一个命令，同时，一个命令最小能够处理的数据只有32个，也使得在实际的并行处理中能够更加的灵活，这就是SIMT结构GPU性能更加优越的原因。

而线程束的存在使得数据处理速度变快的同时，也会带来一个问题，同一个线程束内的32个线程在每个周期内必须执行相同的指令，如果产生了冲突，例如一个线程束内的16个线程需要执行某一条指令，另外16个线程需要执行另一条指令，此时，线程束会先选择其中的一条指令进行处理，同时禁用不执行这个命令的其他线程，这样就会产生线程束分化，而这些被禁用的线程依旧在消耗寄存器资源，就会使得数据处理速度下降，线程束分化的越严重，性能下降越大，并行性削弱也越严重。

要避免线程束分化，除了在伪代码层面要避免之外，在构建逻辑布局的时候就要合理，并且逻辑布局中的线程数量越多，会增加数据处理的速度。因此，在尝试建立不同的逻辑布局时，应该根据线程束的特性来构建网格块和线程块的维度，而这只是建立在理论上，在实际的处理过程中，理论上性能优越的逻辑布局可能会由于多方面因素影响使得数据处理速度达不到期望值。例如，理论上线程数量越大的逻辑布局应当能够提升数据处理速度，但是在实际操作过程中，一个512×512的图片应用线程块为64×1，网格块16×1 024的逻辑布局时，不仅在处理速度上没有线程块为16×1，网格块16×512的逻辑布局块，还出现了数据处理不完全的情况，导致图片数据重建出来之后有些部分还是原图片。这一现象在大量的实验中间歇性的出现在逻辑布局的线程数远超过图片像素的情况下，并且当逻辑布局的维度出现奇数，例如线程块为35×1，网格块15×1 024这样的布局时，这样的现象出现的次数变得更加频繁。

因此，需要通过大量的实验找出能够提升大分辨率图像数据处理速度的，并且是通用的逻辑布局，同时还要避免为了追求处理速度而不断增加线程数量，从而导致数据处理不完全的逻辑布局。而为了避免上文线程束分化的问题，将线程块和网格块的横坐标方向维度定为了16、32、64、128，同时，为了提升数据处理速度，要尽量的增加逻辑布局中的线程数量，在实际的实验过程中，将网格块的纵坐标维度和图像的分辨率大小保持一致的时候数据的处理速度比较块，并且不会出现数据处理不完全的情况。表1挑选了对于不同的逻辑布局下处理一份完整的图像数据的实验中，比较有代表性的实验数据。

表1 不同逻辑布局下数据处理时间 ms

根据表1可以看出，不同的逻辑布局对于不同分辨率图片的处理速度提升效果不一样，对于256×256的图片，线程块为64×1，网格块16×1 024的逻辑布局的线程数量不是最多的，却是数据处理速度最快的，但是这种大线程量的逻辑布局并不适合256×256分辨率的图片，因为在实际的处理过程中出现了数据处理不完全的情况。结合数据处理速度和数据处理完整度，线程块为16×1，网格块16×256的逻辑布局是最适合256×256分辨率的图片的。同时可以看出，随着图像分辨率的增大，线程块为64×1，网格块16×1 024的逻辑布局的数据处理速度一直是比较快的，虽然在实际处理过程中应用在小分辨率图像上时会出现数据处理不完全的状况，但是应用在大分辨率图像的处理过程中，数据处理速度是最快的，并且也不会出现数据处理不完全的情况，因此，通过大量的实验之后，本文对于大分辨率图像的处理应用线程块为64×1，网格块16×1 024的逻辑布局。

3.3 数据分割及改变数据同步方式

与CPU的同步特性不同，核函数的调用与主机是异步的，当完成核函数调用的指令之后，会立即返回，不管运算是否完成，因此CUDA有一个专门的函数是等核函数执行完再进行下一步运算。

基于不同的同步特性，在进行图像的小波变换处理时，通常情况下是将所有数据全部进行小波变换行处理之后，再进行小波变换列处理，接着将处理完成的数据取出进行需要的图像重建之类的工作。这样的方法在图像数据量较小的情况下是没有问题的，但是在图像数据量比较大的时候，就会拖慢数据处理速度。为了改进这个缺点，提高数据处理效率，对这个同步过程进行了分析。这个过程简单来看就是取出数据、行方向变换、列方向变换、图像重建四步，而根据GPU处理数据的速度来看，等待数据全部处理完成再进行下一步是比较浪费资源的，这也是在处理大分辨率数据时速度会比较慢的原因，因此，在这里进行了一个数据的分割之后再进行处理，具体流程为：取出第一份数据进行并行计算，在完成第一份数据的并行行计算后，对第一份数据进行并行列计算的同时，取出第二份数据进行并行行计算；在第一份数据完成并行列计算后，将数据放入上文提到的虚拟地址当中；CPU从虚拟地址中取出第一份数据进行图像重建等操作的同时，第二份数据完成并行行计算，开始进行并行列计算。循环这个过程直到所有数据完成处理。

对于图像数据的分割，需要注意的是在分割的时候是否会造成图像数据的损坏，造成图像特征信息的丢失。本文对图像数据进行分割的时候只是为了将大量数据分成几份，使得每次处理的数据量减小，从而加快数据处理速度，因此这里的分割只是数据量上的分割，不会造成信息的损坏以及特征的丢失问题。将图像数据分割不同的份数时，会获得不同的运行效率，也会出现不同的问题，而根据上文确定的二维线程块逻辑布局，如果分割出的数据量是2的偶数倍的时候应当获得最大的运行效率，如果分割出的数据量是2的奇数倍的时候则有可能会出现运行效率反而降低的情况。因此，在同一个硬件基础上，本文将不同分辨率图像各自分成不同的份数，进行对比实验，如表2所示。

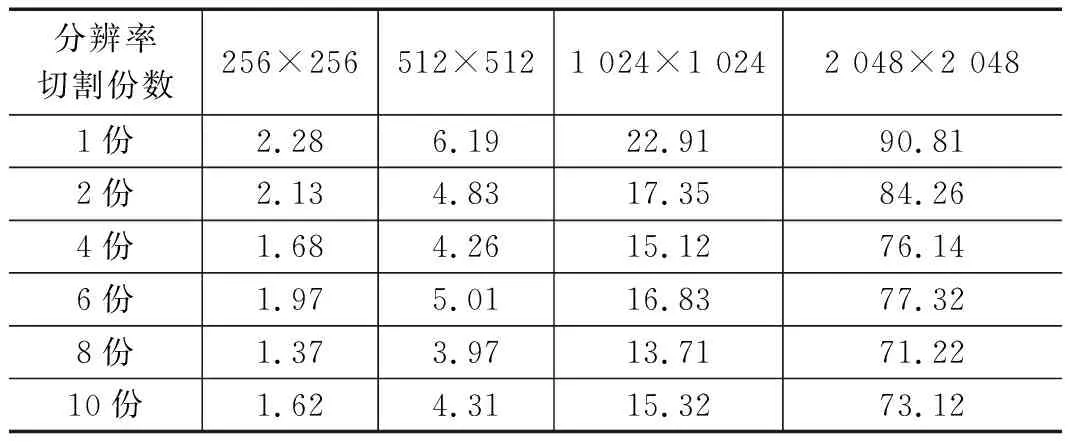
表2 不同分辨率下切割成不同份的数据处理时间 ms

根据表2可以看出，图像分辨率较小的图片，由于本身的数据处理时间就比较小，因此这种切割数据，改变同步方式的方法的提升效果并不是很明显，只有根据减少的时间相对于原始处理时间的比例可以看出还是有些较好的提升效果的。随着图片分辨率的提高，原始处理时间基数的增大，效果也变得逐渐明显，而比较1 024×1 024和2 048×2 048两个分辨率的实验结果可以看出，分辨率越大，提升效果虽然越大，可是相对于原始处理速度，提升的幅度在降低，不过提升的幅度也能达到22%，所以切割数据的方法效果还是较为显著的。

比较1 024×1 024和2 048×2 048两个大分辨率下不同切割份数的效果可以看出，随着切割份数的增多，数据的处理时间不断减小，但是并不是切割份数越多越好，从表2中可看到切割成6份时的处理时间不仅没有减少，反而多于切割成4份时的处理时间，切割成10份的处理时间多于切割成8份的处理时间，因此，将数据切割成2的偶数倍份数是比较合理的，通过对比实验可以得出，切割成8份是效果最好的。

4 实验结果及分析

对于不同的环境，将数据分割所带来的处理速度的提升幅度是一致的，因此只要比较一份完整的数据在哪种环境下处理速度最快，那么将数据分割后的数据处理速度也一定是最快的，因此，本文在CPU环境、SIMD结构的GPU、SIMT结构的GPU下分别对不同分辨率的同一张图片，对二维离散哈尔小波变换的运行时间进行了对比试验。这里所用的CPU芯片型号为AMD Ryzen 7 5800H，SIMD架构的显卡型号为AMD的Radeon RX 6000，SIMT架构的显卡型号为NVIDIA的GeForce RTX 3060，表3列出了不同分辨率在不同环境中的速度，以及是否经过优化的速度。

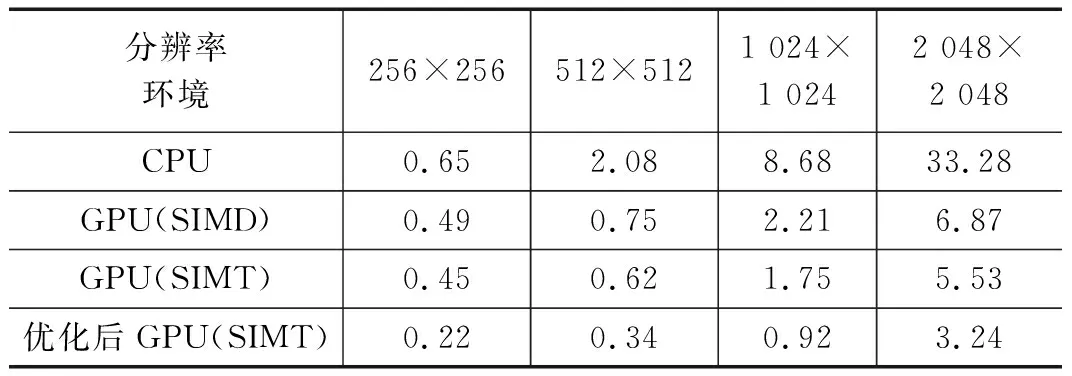
表3 不同分辨率下的小波变换运行时间 ms

单独从小波变换的运行时间来看，从表3中可以看出，图片在小分辨率时，CPU环境下最快运行速度和GPU是相差不大的，随着分辨率的增大，GPU的优势越来越明显，而优化后的GPU程序相对于CPU在2 048×2 048时提升幅度最大，为90.3%，相对于原始GPU程序的提升保持在40%以上，从架构上来看，SIMT架构的GPU比SIMD架构的GPU最大快19.5%左右。

考虑到整个过程是包含图像数据的读取、GPU加载数据时间、小波变换计算时间以及内存读取结果并重建成图像的时间。因此表4比较了CPU环境下最快运行速度的运算以及GPU环境下最快运行速度的情况。

算上总体时间后，在图片分辨率大于512×512之后，GPU的优势就已经体现的较为明显，分辨率大于1 024×1 024之后，SIMT架构的GPU的优势也展现出来了，根据表4的数据，SIMT架构对比SIMD架构的提升幅度最大为16.3%。SIMT架构GPU对比CPU最大提升幅度为51.1%，提升幅度没有只计算小波变换时间的幅度大，因为GPU计算是有部分操作要先在CPU里做，提升的只有数据送进GPU里之后的运行速度，从时间上来看，已经能够达到实时处理的目的。

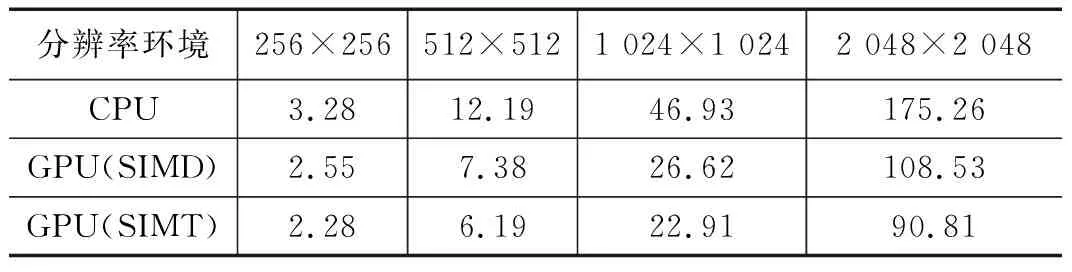
表4 不同尺寸的整体运行时间 ms

5 结束语

针对大分辨率图像处理实时性不足的问题，本文通过GPU有大量可编程核心的特点，采用了SIMT结构的GPU对小波变换进行并行公式推导，通过大量的实验，找出了SIMT结构GPU下，对于大分辨率图像处理速度最快，并且不会出现数据处理不完全情况的逻辑布局，在这种逻辑布局下，进一步的将数据分割，改变了数据处理的同步方式，通过实验对比得出，针对大分辨率图像，将数据分割成8份是处理速度最快的，同时改变了内存的寻址方式，通过虚拟寻址进一步提高了数据处理速度，并简化了伪代码，在整体上提高了小波变换的运行效率。同时，实验通过对一份完整的大分辨率图像数据，比较了CPU环境下的串行算法和SIMT、SIMD架构的GPU环境下的并行算法以及优化后的算法，表明了在小波变换计算的效率上，随着分辨率的增加，SIMT结构GPU相对于CPU效率最大可到90.3%，SIMT比SIMD架构的GPU效率高19.5%，优化后的程序比优化前的效率随着分辨率增大最大可提升47.4%。在整个完成过程，包含了数据读取、数据加载、小波变换以及内存读取并重建图像的时间上，SIMT结构GPU相对于CPU效率提升最大可到51.1%，SIMT比SIMD架构的GPU效率高16.3%，表明了SIMT结构GPU具有优越性，并且达到了实时处理的目的，同时，本方法也可移植于同类问题。