基于噪声统计的EMD-LSTM网络流量预测方法

谷妙春

(南京理工大学 计算机科学与工程学院,南京 210094)

0 引言

5G等技术的不断发展促进了各类网络服务的大量应用，这对网络的性能及服务质量有了更高的要求。流量预测[1]作为网络管理、调控的重要方式之一，利用数据流当前和历史的流量状态数据来预测下一时段的流量状态[2]。准确的预测结果有助于优化资源配置，提高生产效率，实现供需匹配。

近年来，随着机器学习的发展，许多学者使用递归神经网络(RNN, recursive neural networks)模型预测流量[3-5]。相比于传统的自整合移动平均自回归模型[6-8]、广义自回归条件异方差模型[9-11]等预测方法，RNN通过捕获流量序列的高维特征学习流量序列时序关联性，避免了繁杂的函数拟合且具备更准确的预测效果。但传统RNN存在梯度消失或爆炸问题，不具备长期依赖性[12]。长短期记忆(LSTM， long short term memory)作为RNN的变种克服了上述梯度问题，可应用于短期与长期的流量预测。目前基于LSTM的流量预测方法广泛应用于各类生产活动中[13-15]。

大量的动力学研究表明，现实中的人类活动普遍遵循着一定的规律性[16]，例如对某一固定区域而言，其流量的总体趋势往往表现出一定的周期性，基于这种周期性可以知道下一周期内流量的大致趋势，这对流量预测有着积极的意义。但同时具体的流量数值会受个体随机活动影响表现出很大的不确定性，并且这种数值波动具有非平稳非线性的特点，这又为流量预测带来了一定难度。从信号处理的角度分析，可以将实际的流量看成实际信号，总体的流量趋势看成有用信号，流量的波动看成噪声信号，实际信号即受噪声信号影响围绕有用信号波动。在LSTM预测中，通过对实际信号降噪，改善有用信号与噪声信号的信噪比，从而有助于LSTM正确学习有用信号，使得预测结果最大程度贴合实际信号的变化趋势，从而提高预测精度。因此在LSTM预测前需要对若干周期的原始流量进行降噪处理。

常见的信号降噪方法包括傅里叶变换[17]、小波变换[18-20]、经验模态分解[21-23](EMD， empirical mode decomposition)等。相较于傅里叶变换与小波变换，EMD具备自适应性，无需选取基函数，可处理平稳与非平稳序列，克服了傅里叶变换与小波变换的局限性。但现有的EMD降噪方法多是基于单个信号的降噪：文献[21-22]对EMD分解后的不同本征模态函数(IMF，intrinsic mode function)使用不同阈值降噪，但这种做法由于抑制了高于阈值的数值，会在一定程度上破坏实际信号的变化趋势，不能使LSTM正确学习有用信号；文献[23]基于高斯白噪声统计平均为零的特性将一个含有高斯白噪声的流量序列反复叠加不同随机过程的高斯白噪声以实现降噪。但这种做法由于不确定原始序列中高斯白噪声的模值需要反复叠加，导致降噪效率低下，并且将任意噪声视为高斯白噪声只是一种“近似替换”，实际中的噪声并不一定完全具有高斯白噪声的统计特性，从而不一定能有效、正确抑制噪声。在LSTM中使用EMD降噪训练样本也多延用上述EMD降噪思路：除了使用上述降噪方法外，文献[24-25]基于互信息选择部分由EMD分解后的IMF将实际信号重构进行预测，但这种做法仍存在趋势破坏问题；文献[26]使用某一样本与其临近的序列的平均值作为该样本的降噪结果，但如果选取的临近序列少会影响降噪效果，如果选取的临近序列多同样会破坏实际信号的变化趋势。此外，上述LSTM预测方法多着眼于通过降噪训练样本提升预测准确性，但对训练样本的构造缺乏讨论。考虑到序列的时间关联性，上述的LSTM预测方法均采取滑动窗口连续的批量输入样本，这会导致长期预测中的误差累积问题，因而只对中短期的预测结果较好。

事实上，每个LSTM训练样本中已经包含了噪声的一次随机过程，可将这些噪声信号从训练样本中提取出来，通过分析这些噪声信号确定噪声的统计特性。因此，本文在降噪方法上提出一种基于噪声统计的EMD降噪方法：在给定若干流量序列的情况下，将每一流量序列进行EMD分解，基于分解后各IMF的能量筛选出含噪较高的噪声IMF，将这些IMF进行统计平均得到对应的降噪IMF，使用降噪IMF替换噪声IMF再与非噪声IMF重构流量序列实现流量序列的降噪，并将降噪后的流量序列作为LSTM训练样本。这样既保留了原始流量序列的变化趋势，又充分利用各个样本中包含的噪声，既无需事前知道噪声的统计特性又具有较高的降噪效率。同时在训练样本构造上使用间隔采样选取临近数据与历史同期数据，减少连续滑动窗口带来的累积误差。由此构成的LSTM预测模型称为EMD-LSTM预测模型。此外，目前对无人机(UAV， unmanned aerial vehicle)的应用研究多是优化UAV的活动状态或轨迹实现收益最大化[25]，但对UAV何时返航充电的问题鲜有讨论，文献[27-29]均默认UAV电量耗尽时返航充电。本文将该预测模型应用于一种基于UAV卸载流量的蜂窝网络，通过该预测模型分析UAV在长时间工作下何时返航充电可最小化服务中断时间，提出一种基于EMD-LSTM的UAV活动规划方法以完善当前对UAV完整活动流程缺乏讨论的问题，同时具体说明流量预测如何有助于优化资源配置。

综上，本文工作及创新点如下：

1)提出一种基于噪声统计的EMD降噪方法，该方法相比于传统EMD降噪方法无需获取噪声的先验知识，避免因超参设置不当影响降噪效果，同时充分利用样本中噪声的随机过程，具备较高的降噪效率。

2)使用基于间隔采样的LSTM训练样本构造方法，减少预测中的误差累积问题，提升中长期预测的准确性。

3)将该模型应用于一种基于UAV卸载流量的蜂窝网络，提出一种基于EMD-LSTM的UAV活动规划方法，以最小化服务中断时间为目标优化UAV在长时间工作下返航的时间点。

1 EMD分解

EMD通过将一个序列分解为若干不同尺度的平稳波动项和一个残差向的叠加，其本质是将非平稳序列平稳化过程。EMD分解中每一个平稳波动项称之为一个IMF。对于每一个IMF，需满足以下两个条件：

1)IMF的极值点和过零点的数目相等或只相差一个。

2)IMF的上包络线和下包络线关于时间轴对称，即两条包洛线在每一个时间点处的均值为0。

假设蜂窝网络在周期T内产生的流量序列为D(t)，D(t)表示如下：

D(t)={D(1),D(2),…,D(T)}

(1)

将D(t)按如下方式进行EMD分解：

1)确定T内D(t)的全部局部极大值和极小值，通过三次样条插值法求出D(t)的上包络线U(t)和下包络线L(t)；

2)求出上下包络线的中位线M(t)，M(t)的表达式如下：

(2)

将D(t)减去M(t)得到准IMF分量ψ1(t)，ψ1(t)的表达式如下：

ψ1(t)=D(t)-M(t)

(3)

3)判断ψ1(t)是否满足IMF条件，如果是，则ψ(t)为第一个IMF分量，记为imf1，如果不是，则对ψ1(t)依照D(t)做相同计算得出ψ2(t)，判断ψ2(t)是否满足IMF条件或停止条件SD，如果是则ψ2(t)为imf1，否则重复上述步骤计算ψk(t)，直到ψk(t)满足IMF条件或停止条件SD，其中停止条件SD如下：

(4)

当SD小于预设的典型值时即可认为ψk(t)满足IMF要求，一般典型值在区间[0.2,0.3]设置。

4)计算R1=D(t)-imf1，将R1作为新的待分解序列，重复上述步骤以此计算imf2，imf3，…，imfn，直到Rn为单调序列或常值序列。此时可以将序列D(t)表示为：

(5)

至此D(t)的EMD分解完成，需要指出的是先分解出的IMF分量为原始序列高频分量，也是高噪部分，后分解出的IMF分量为原始序列低频分量，伴随着较低的噪声，Rn为残差项，反映出D(t)的总体变化趋势。

2 基于噪声统计的EMD降噪

EMD降噪的原理是通过计算各IMF分量的能量来划分低频分量与高频分量，对含噪较高的高频分量进行一定的处理以抑制其能量，从而实现降噪。对任意IMF，其能量的计算方式如下：

(6)

式中,imfk(t)表示t时刻imfk的值。显然，k越大，即IMF分量频率越低，E(imfk)越大。IMF能量从高频到低频存在突变，找到突变位置即可区分高频IMF与低频IMF。突变点K0的计算方法如下：

(7)

(8)

找出突变点K0后，对IMF高频部分，即imf1，imf2，…，imfK0进行降噪，记降噪后的结果为φ(imf1)，φ(imf2)，…，φ(imfK0)。将降噪后的高频部分与原始序列的低频部分及残差项进行重构，即可实现对原始序列D(t)的降噪。降噪结果φ(D(t))表示如下：

(9)

φ(imfk)的计算依赖于其它原始序列经EMD分解后的IMF。假设从该蜂窝网络采集M个D(t)序列，记第m个D(t)序列为Dm(t)，分解后的结果为imfk,m，则φ(imfk)与φ(Dm(t))的计算过程如下：

1)对M个D(t)序列依次进行EMD分解，得到Dm(t)分解结果为imf1,m，imf2,m，…，imfn,m。

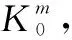
(10)

式中,round(K)表示对K就近取整。此时任意样本Dm(t)可以表示为：

(11)

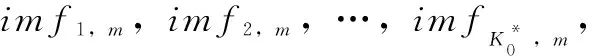
(12)

4)将降噪后的高频分量与Dm(t)中低频分量和残差项重构，可得Dm(t)的降噪结果为：

(13)

由此实现了对m个D(t)序列的降噪。

3 基于间隔采样的训练样本构造

由于时间序列的连续性，常见的训练样本构造方法是采用滑动窗口输入序列作为LSTM的输入，但这种方法在预测长期数据时存在误差累计问题。假设对于序列{D1(t),D2(t),…,DM(t)}，窗口大小为θ，在训练LSTM预测Dm(t)时输入的训练样本为{Dm-θ(t),Dm-θ+1(t),…,Dm-1(t)}。这种输入方法会导致LSTM在预测长期结果时会在短期预测结果的基础上预测。例如预测DM+2(t)，LSTM需要的输入为{DM-θ+2(t),…,DM(t),DM+1(t)}，而DM+1(t)是LSTM基于序列{DM-θ+1(t),…,DM-1(t),DM(t)}的预测结果，这会降低LSTM对DM+2(t)预测的准确性。

鉴于流量序列具有周期性的特性，可以采用间隔采样的方式基于若干历史同期数据构造训练样本。假设间隔尺度为ε，在训练LSTM预测Dm(t)时可构造训练样本{Dm-θε(t),Dm-θε+ε(t),…,Dm-ε(t)}。这样在预测未来多个周期的流量序列{Dm1(t),Dm2(t),…,Dmn(t)}时，使用间隔采样法在预测Dmi(t)(1≤i≤n)时对应的输入序列为：

{Dmi-θε(t),Dmi-(θ-1)ε(t),…,Dmi-ε(t)}

(14)

而使用滑动窗口法预测Dmi(t)时对应的输入序列为：

{Dmi-θ(t),Dmi-(θ-1)(t),…,Dmi-1(t)}

(15)

与滑动窗口相比，这样的间隔采样方法在输入序列长度不变的情况下尽可能减少使用LSTM预测结果再预测，从而减小累计误差，提升预测准确性。

4 基于EMD-LSTM的UAV活动规划

基于上述讨论，本文提出一种基于噪声统计特性的EMD降噪方法与LSTM结合的流量预测模型：EMD-LSTM模型。首先采集连续M个周期的流量序列D(t)；其次对每一序列Dm(t)进行基于噪声统计特性的EMD降噪，得到降噪后的训练样本φ(Dm(t))；接着构造大小θ，间隔尺度为ε的序列构造LSTM中预测φ(Dm(t))的训练样本；最后将训练好的LSTM用于预测未来周期的流量数据，其输入仍为以同样方式构造的间隔采样序列。

假设某蜂窝网络由1个宏基站、X个潜在热区和X架UAV组成，每架UAV为一个潜在热区卸载流量。考虑到所有潜在热区在卸载流程上是等效的，这里以其中一个潜在热区为例。简化后的网络结构如图1所示。

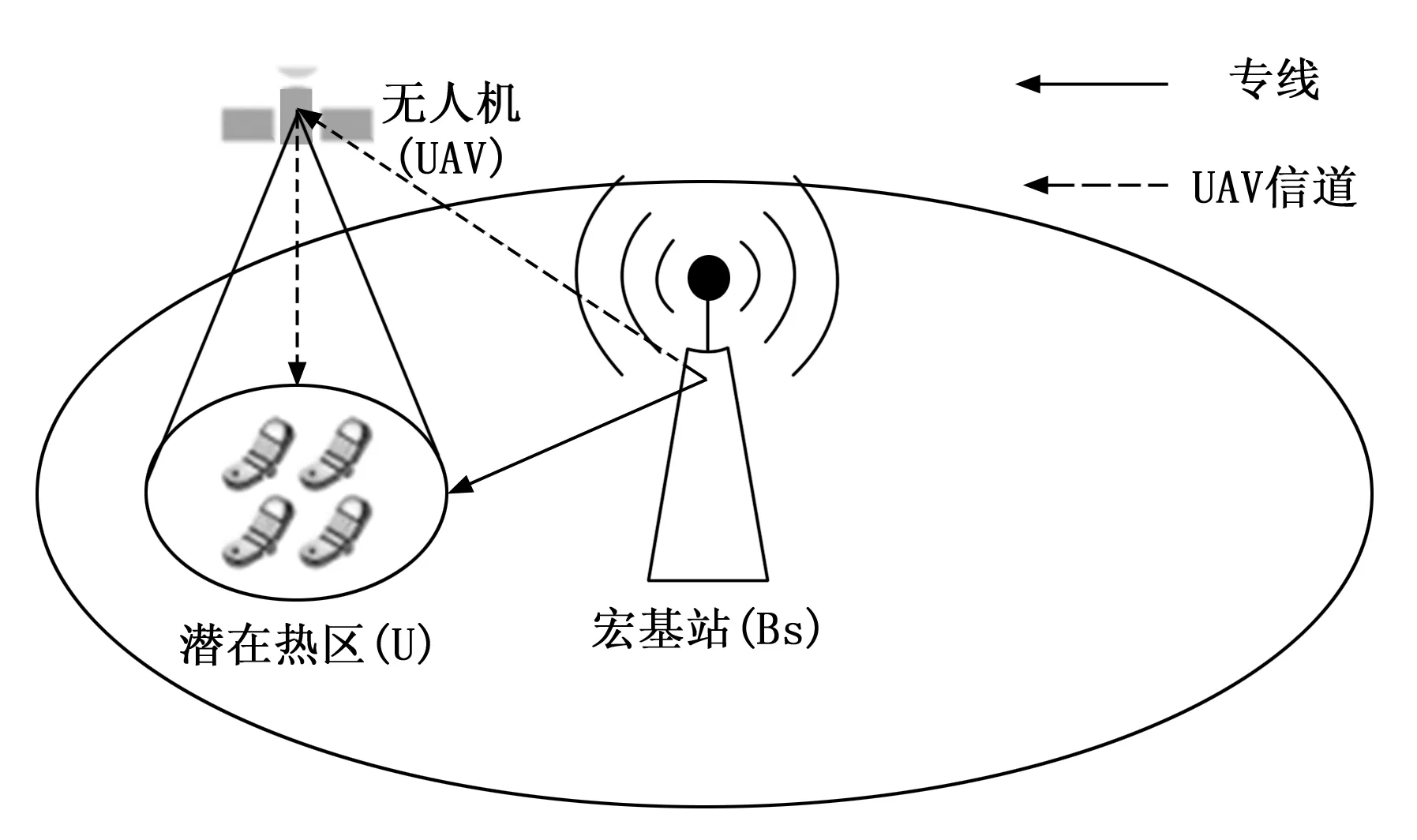
图1 蜂窝网络结构

宏基站BS中存在一个缓存队列Q以缓存潜在热区U请求的数据，假设t时刻U请求的数据量为D(t),记Q(t)表示t时刻Q中的数据量。BS可使用一专线以固定速率Q0向U发送数据，同时当Q(t)+D(t)-Q0>0时可使用UAV以固定速率Q1发送数据，记ΔQ(t)=Q(t)+D(t)-Q0，则下一时刻Q(t+1)的表达式如下：

(16)

由于UAV续航有限，为了尽可能延长UAV的使用时间，当UAV在t时刻发送数据时，UAV应处于激活状态；而当UAV在t时刻未发送数据时，UAV应处于休眠状态。记a(t)表示t时刻UAV的活动状态，a(t)=1表示UAV处于激活状态；a(t)=0表示UAV处于休眠状态。当ΔQ(t)≤0时UAV处于休眠状态；当ΔQ(t)>0时UAV处于激活状态。基于BS对U若干历史周期流量序列的采样，使用本文所提EMD-LSTM模型预测U未来一段时间的流量数据，根据ΔQ(t)的数值可以知道对应a(t)的取值，即当前时刻UAV是否应活动，进而结合式(16)可知所预测时间段内UAV的活动序列与队列长度的序列。

记UAV的电池容量为C，UAV处于激活状态伴随着c1的电量消耗，而当UAV处于非激活状态时由于其本身的悬停、移动也伴随着c2的电量消耗。当UAV电量即将耗尽时，UAV需返回充电处充电。假设U距UAV充电处的距离为l，UAV的飞行速度为v，充电时间为t0。易知UAV往返充电处与U需要的最小时间tc为：

(17)

于是UAV的活动规划方法如下：

步骤1：UAV更换好电池从充电处飞往U处待命。

步骤2：当UAV飞至U处时，记该时刻为零时刻。基于LSTM对D(t)的预测结果可知在未来τ时刻内UAV的活动状态序列为{a(0),a(1),…,a(τ)}。考虑到UAV需预留返回充电处的电量，则UAV可为U提供服务的最大时间τ1满足：

(18)

式中,1x表示当条件x为真时，1x=1，否则1x=0。

记该状态序列中UAV首次激活的时间点为τ0。如果在[τ0,τ1+tc]时间段内存在某个时间点τ2满足：

(19)

式中,τ2∈[τ0,τ1]。

式(19)表示UAV在τ2时刻后的接下来tc时间段内均处于休眠状态，UAV可在此时间段内返回充电而不造成服务中断，由此构成的满足条件(19)的τ2的集合为R2；如果R2=φ，为了尽可能减少服务中断，UAV应在[τ0,τ1+tc]时间段中选择时间点τ3，这样的τ3满足其后的tc时间段内处于休眠的时间大于等于[τ0,τ1+tc]时间段中任意tc时间段内处于休眠的时间，即解方程：

(20)

式中，τ3∈[τ0,τ1]，UAV可在τ3时刻返回充电。记方程(20)的解τ3构成的集合为R3。

步骤3：为了避免UAV频繁往返充电，如果R2≠φ，取R2中的最大值作为UAV返回充电的时间点；如果R2=φ，取R3中的最大值作为UAV返回充电的时间点。记返回充电的时间点为τ4。

步骤4：对于UAV返回充电前的任意时刻t∈[0,τ4]，当a(t)=0时，UAV处于休眠状态；当a(t)=1时，UAV处于激活状态并提供传输服务。

步骤5：当t=τ4时，UAV返回充电。

5 仿真实验

为了能真实反映现实生活中蜂窝流量的特性，仿真选取的数据集为WIDE骨干网中采样点F于2021年5月1日至2021年6月30日采集的总流量数据[30]。该数据由MAWI Working Group与WIDE Project提供。该采样点记录了其上游网络提供商每日的流量数据，采样间隔为10分钟。

基于数据集的实际意义，仿真中T=144代表每日流量数据；ε=1 008代表历史每周同期流量数据；θ=1 008代表一周流量数据。其余参数为：Q0=300；Q1=150；l=3 000；v=3 000；C=120；t0=24；c1=2；c2=1。LSTM由一个输入层、一个LSTM层、一个全连接层、一个回归层构成。LSTM层有200个隐藏单元，解释器为Adam，初始学习率为0.005，每迭代125次乘以因子0.2降低学习率。61个样本中前56个样本用于训练LSTM网络，后5个样本用于测试，迭代次数为500。

图2和图3分别给出了不同工作日和休息日下每日采集的流量数据。

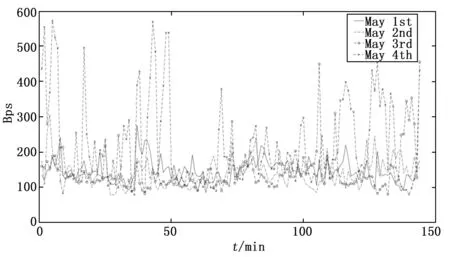
图2 不同休息日的流量数据

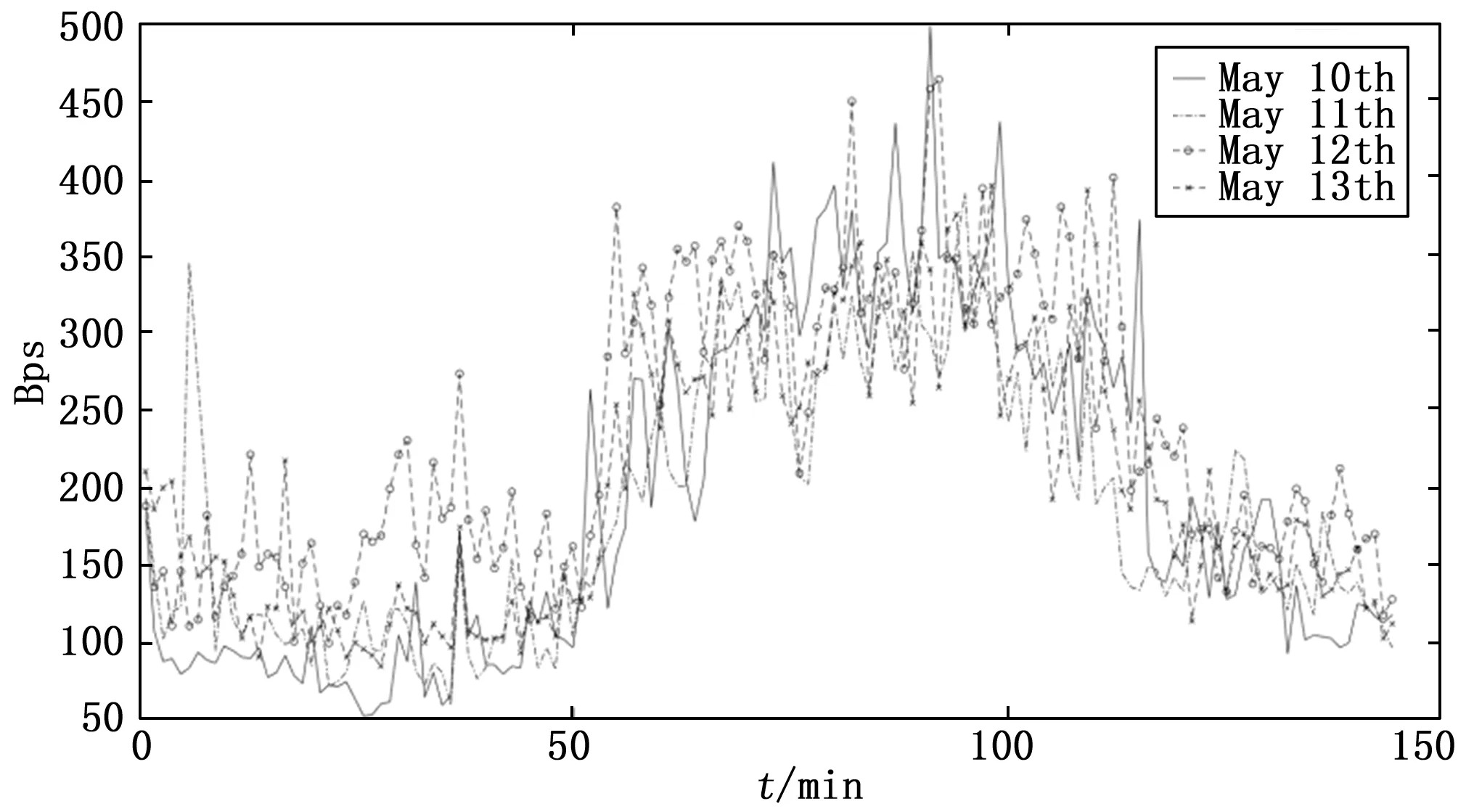
图3 不同工作日的流量数据

该数据集中每日的流量变化趋势受人类休息日与工作日影响大致为两种。根据图1可知，在休息日中，流量不存在明显的变化趋势；在工作日中，流量存在一个大致在每日早9点至晚9点的流量高峰。同时，不同工作日与休息日下的流量大小与变化趋势虽大致相同但存在明显的波动。此外，除节假日因素外，休息日下的流量趋势只可能出现在每周的周六或周日。实例表明流量具有周期性和高噪声的特点。

图4以5月1日的流量数据为例给出了文献[19]、文献[21]与本文所提EMD降噪方法的降噪效果：

图4 不同EMD降噪方法的降噪效果

不难发现，只有本文所提EMD降噪方法获得了比较理想的降噪效果，这是因为文献[19]采用的阈值法只会对超过阈值的部分降噪，因而降噪效果有限；文献[21]采用的基于高斯白噪声统计特性的方法在面对非高斯白噪声或未知统计特性的噪声时，并未基于实际噪声的统计特性降噪，因而降噪效果不理想。只有本文所提降噪方法无需获取噪声先验知识，通过提取训练样本中的噪声，分析其统计特性后降噪，获得了相对理想的降噪效果。

图5展示了以不同降噪方法的结果作为LSTM输入并使用滑动窗口法构造训练样本时LSTM对6月25日至6月30日流量的预测结果。

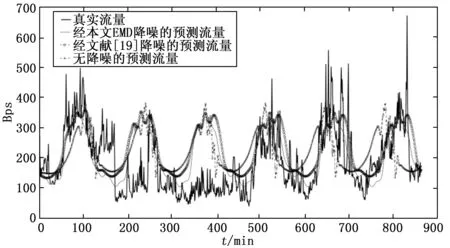
图5 滑动窗口下不同降噪方法预测结果

根据图5可知，使用本文EMD降噪方法后的LSTM预测结果相较于使用传统EMD降噪与未降噪的预测结果更接近真实流量。但三者在预测6月27日的流量时均认为流量趋势为工作日而非休息日，这是因为休息日相较于工作日属于偶发的短期事件，基于滑动窗口输入训练样本时休息日的流量数据将作为短期事件被LSTM网络“忘记”，因而这种样本构造方式使得LSTM对未来每一天流量的趋势预测均为工作日的趋势。

而使用间隔采样方法构造训练样本后LSTM的预测结果如图6所示。

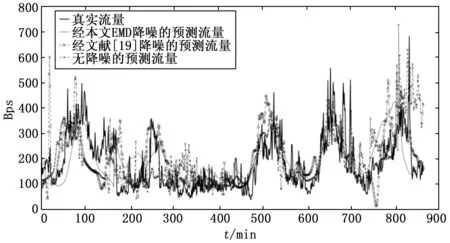
图6 间隔采样下不同降噪方法预测结果

根据图6可知，使用本文EMD降噪方法后的LSTM预测结果依然优于传统EMD降噪以及无降噪的预测结果，并且LSTM能正确预测6月27日的流量趋势为休息日，这是因为对于每周日而言休息日属于高频的长期事件，即使其中混入部分工作日LSTM网络也会将这些休息日下的工作日视为短期事件而“忘记”，因而能正确预测未来流量趋势。因此本文提出的EMD-LSTM预测模型相比于传统EMD-LSTM预测模型具备更好的预测效果。

为了量化不同方法的预测结果，本文选用平均绝对百分比误差(MAPE， mean absolute percentage error)、均方根误差(RMSE, root mean square error)评估不同方法下的预测结果与真实值之间的差异程度，结果如表1所示。

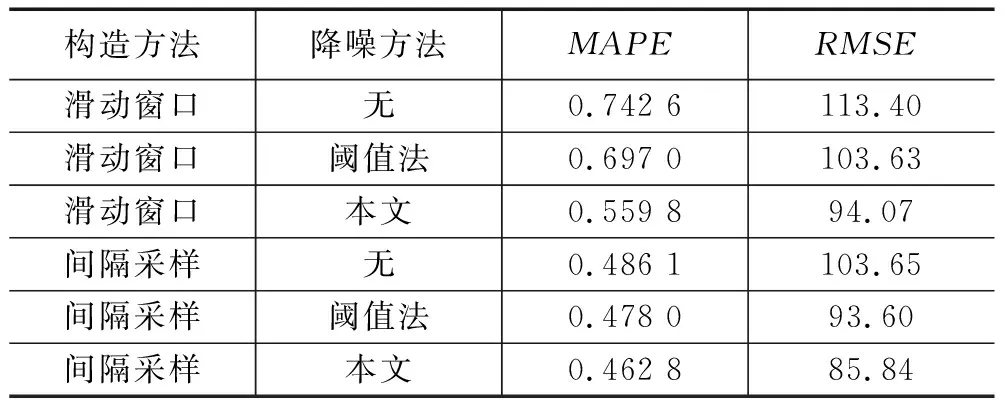
表1 不同方法的LSTM预测效果

综上，本文所提EMD-LSTM预测模型相比传统EMD-LSTM模型具备更优预测结果。

最后，图7对比了6月25日至6月30日使用本文提出的UAV活动规划方法与使用目前UAV电量耗尽即返航充电的传统活动方法时Q的变化以及在使用本文提出UAV活动规划方法而使用不同EMD-LSTM预测模型时Q的变化。

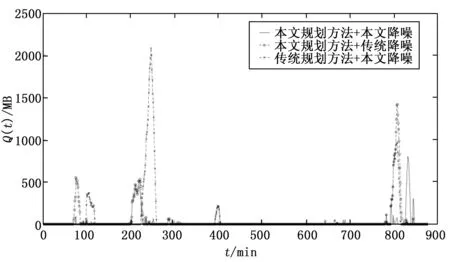
图7 不同UAV活动方法对Q的影响

根据图7可知，传统的UAV活动规划方法并未考虑UAV的后续使用问题，因而可能会在某些热区存在时段因电量不足而返航充电，从而导致突发数据不能卸载，使得缓冲队列中的数据量激增。即主要对应图7中[235，265]时间段；而本文提出的UAV活动规划方法则考虑了UAV后续的使用问题，选择最大续航时间下可工作时间段中中断时间最短的时间点返航充电以尽可能减少突发数据因UAV返航而无法卸载的问题，因而相较于传统UAV活动规划方法缓存队列不存在激增的情况。虽然因为预测精度问题导致缓存队列的使用频率小幅上升，但总体而言使用本文所提UAV活动规划方法不仅大幅减小了缓存队列的平均长度，还可以在同等条件下使用更小的缓存队列应对突发流量。而在同样使用本文所提UAV活动规划方法的前提下，使用传统的EMD-LSTM预测模型因为不能准确预测未来的流量趋势，因而不能准确控制UAV激活的时间点，从而会在某些需要UAV卸载流量的时间段因未激活UAV导致缓存队列中存在较多的数据。分析数据可知，使用本文所提UAV活动规划方法并结合本文所提预测模型所需缓冲区最小大小为806，平均队列长度为22.11；使用本文所提UAV活动规划方法但使用传统预测模型所需缓冲区最小大小为1 416，平均队列长度为38.92；而使用传统UAV活动规划方法所需缓冲区最小大小为2 079，平均队列长度为65.70。因此本文提出的UAV活动规划方法既降低了平均缓存队列长度，又节省了缓冲区空间，结合本文所提EMD-LSTM预测模型，进一步强化了效果。

6 结束语

本文基于实际蜂窝流量具有周期性的特点，结合若干历史周期流量数据使用LSTM预测未来周期流量。为了提高预测精度，提出一种基于噪声统计的EMD降噪方法对训练样本降噪；提出使用间隔采样的方法构造训练样本。此外，本文结合实例说明流量预测如何指导生产生活，通过本文提出的EMD-LSTM模型规划UAV未来一段时间的活动状态，从而选择合适的时间段返航充电，减少UAV的服务中断，提升了卸载性能。