耦合电感集成型谐振变换器及其自适应频率控制

徐菁涛 许 国 孙 尧 熊文静

（中南大学自动化学院 长沙 410083）

0 引言

近年来，LLC 串联谐振变换器因其高效率、高功率密度和软开关特性等优点被广泛应用与新能源发电系统、电动汽车充电、LED 驱动等领域[1-4]。传统的LLC 串联谐振变换器采用脉冲频率调制（Pulse Frequency Modulation,PFM），然而当电压范围变换较宽时，开关频率会偏离谐振频率点，变换器中会产生较高的环流，导致损耗增加，转换效率降低[5-6]。

为了在较窄的开关频率调节范围内实现宽电压增益，学者们提出了一些优化的控制策略。文献[7]提出了一种 LLC 谐振变换器的移相调制（Phase Shift Modulation,PSM）策略，其开关频率始终等于谐振频率，但是变换器的关断损耗较高。文献[8]提出了一种 PSM 和脉冲宽度调制（Pulse Width Modulation,PWM）混合调制策略，两种调制策略分别应用于不同的电压范围，能够兼顾调压能力和转换效率，但是该调制策略较为复杂。文献[9-10]提出了一种多模式控制，通过工作模式的切换，变换器的结构能够改变，使得电压范围有效拓宽，但是，该方法难以实现多模式的平滑切换。改进变换器的拓扑结构是拓宽调压范围的另一种有效途径。文献[11-12]在变换器二次侧添加了辅助开关，能够在固定开关频率下获得更宽的电压增益，但是，变换器的模态和控制逻辑变得更加复杂。文献[13]添加了辅助变压器，能够改变谐振变换器的等效电压比，但是辅助变压器的利用率较低，导致整体的功率密度下降。文献[14]在变压器端口上并联了一组LC 网络以实现宽电压增益，但是谐振网络的分析和设计较为复杂。

尽管改进的调制策略和拓扑结构能够在一定程度上提升调压范围，但是变换器的控制策略以及电路模态的复杂度也随之增加。两级式级联拓扑能够有效地解决这个问题[15-16]。通常，两级式拓扑可由非隔离PWM 变换器（如Boost 变换器）和LLC 谐振变换器组成。在这类拓扑中，谐振变换器的开关频率等于谐振频率，仅作为直流变压器实现单位电压增益。整体的电压调节由非隔离PWM 变换器实现。与单级结构相比，两级式拓扑的调压能力得到有效提升且控制策略更加简单。此外，两级结构采用了较多的开关管与磁性元件，整体的体积与成本较高。为了解决这个问题，采用全桥结构，如图1a所示。一些文献采用了半导体器件的复用技术[17-20]，通过复用交错Boost 电路与全桥谐振变换器的一次侧桥臂，开关管数量得以有效减少。这个思路也可以应用到半桥结构上[21-22]，半桥结构变换器的一次侧仅需使用两个开关管。半桥结构如图1b 所示。

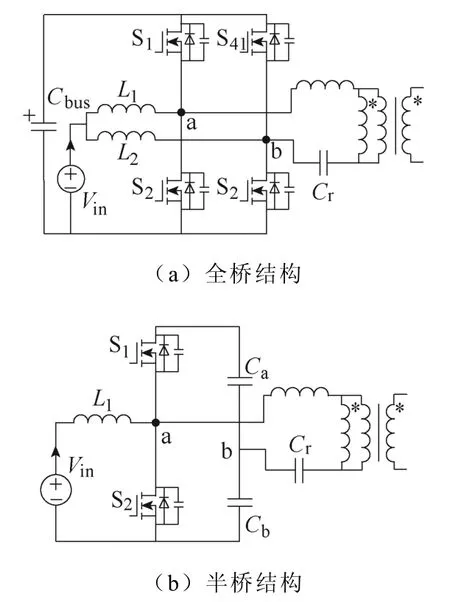
图1 Boost-LLC 谐振变换器集成拓扑结构Fig.1 Boost LLC resonant converter integrated topology

与两级式拓扑结构相比，开关复用后，有效地减少了半导体器件和驱动电路的数量，但是依然存在一些缺失。首先，复用拓扑需要添加额外的Boost电感，这会降低整体的功率密度；其次，在复用结构中，Boost 级需要通过占空比调节电压增益，而占空比的变化同样会影响谐振级的电压增益，这会使得变换器整体的电压控制变得更加复杂，并且增益特性还会随负载变化。此外，由于Boost 变换器电流和谐振电流的叠加，会使得一次侧开关的零电压软开关（Zero Voltage Switching,ZVS）分析变得困难。因此，复用后的拓扑，在分析和设计上的复杂度与约束条件相对较高。

本文针对半桥谐振拓扑结构，提出了一种耦合电感集成型的谐振变换器（Coupled Inductor integrated Series Resonant Converter,CISRC），其拓扑结构如图2 所示。除了将Boost 级和谐振级的开关桥臂复用以外，还采用了耦合电感将Boost 电感与谐振级的高频变压器集成，因此无需添加额外的Boost 电感，集成后的拓扑仅需一个磁性元件（耦合电感）。本文所提出的CISRC 通过占空比调节输出电压，而在所提出的调制下，谐振级始终能够实现单位电压增益而不受占空比影响。因此整体的电压控制更加简单，且与负载无关。而且，谐振电流始终为正弦半波，在开关动作时刻等于零，因而在分析ZVS 时，可以简化。另外，为了优化电流纹波，本文还提出了一种无电流传感器的自适应频率控制。因为励磁电流无法直接通过采样得到，因此本文通过设计电流观测器估计得到励磁电流的平均值，以此来计算并调节最优开关频率。

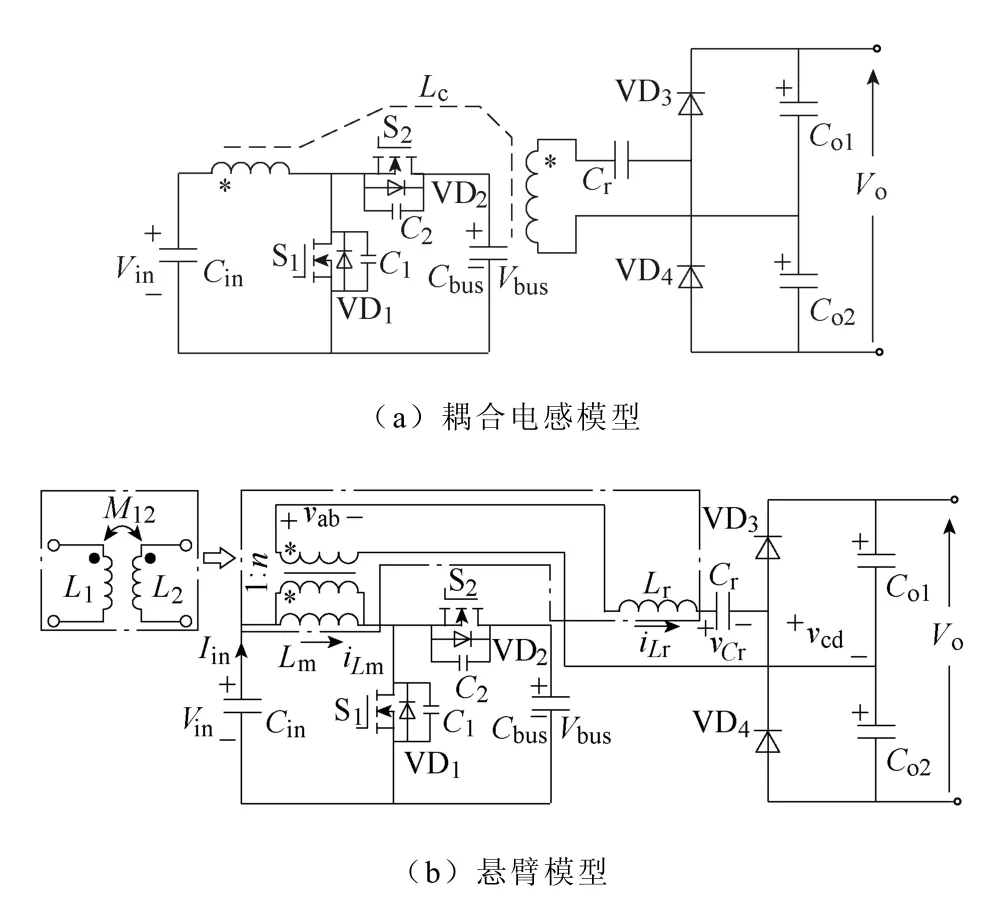
图2 所提出CISRC 的拓扑结构Fig.2 Topology of proposed CIBSRC

1 拓扑结构与工作原理

1.1 拓扑结构

为了便于分析，将耦合电感等效变换为悬臂模型，如图2b 所示。耦合电感分为理想变压器、励磁电感Lm和漏感（谐振电感）Lr。其中，励磁电感也作为Boost 级储能电感，漏感作为谐振电感。S1和S2同时构成Boost 级的桥臂与谐振级一次侧桥臂，VD1和VD2为体二极管，C1和C2为结电容，VD3和VD4为二次侧整流二极管，此外，Co1和Co2为输出电容且两者容值相同。理想变压器电压比为1∶n。谐振电感Lr和谐振电容Cr构成谐振网络，谐振频率为

1.2 工作原理

CISRC 的工作波形如图3 所示。S1和S2互补导通，定义D为S2的占空比。谐振腔的输入电压vab为高频方波同时也是Boost 电感的端电压。此外，励磁电流始终连续并且具有负值，以此来实现一次侧开关的ZVS。谐振电流为正弦半波，并且在开关的切换时刻等于零。Co1和Co2的电压相等，而谐振电容Cr的电压有直流偏置。占空比小于0.5 和大于0.5 的工作原理类似，因此本文仅详细讨论小于0.5的情况。

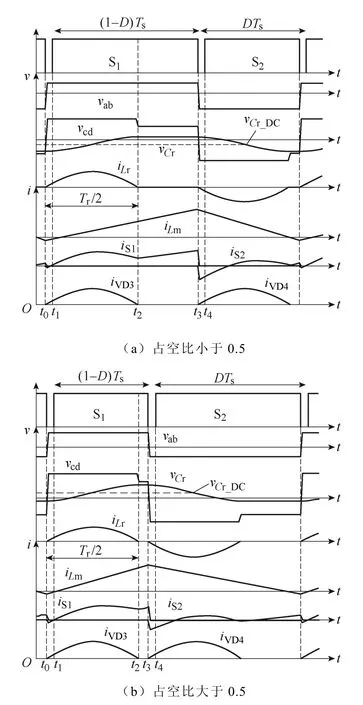
图3 CISRC 的工作波形Fig.3 Working waveforms of CISRC

阶段1[t0,t1)：在t0时刻，所有开关都关断。iLm反向通过二极管VD1并流入Cin。谐振电流从零开始增加，通过二极管VD3给Co1充电。这个阶段，谐振网络中各个元件的电压、电流表达式为

阶段2[t1,t2)：在t1时刻，S1实现ZVS 开通，由于谐振腔的端电压vab保持不变，因此谐振腔的各个元件的电压、电流表达式与阶段1 中的相同。在这个阶段，谐振电流会完成正半周期的谐振，而励磁电流会持续增加到峰值。

阶段3[t2,t3)：在这个阶段，S1保持开通。而在t2时刻，谐振电流已经完成正半周期的谐振，因此等于零，而二极管 VD3可以实现零电流软开关（Zero Current Switching,ZCS）关断。这个阶段谐振腔的工作状态可以表示为

阶段4[t3,t4]：在t3时刻，所有开关都关断。iLm通过二极管VD2为Cbus充电，并从峰值开始减小。谐振电流从零开始反向增加，通过二极管 VD4给Co2充电。这个阶段，谐振网络中各个元件的电压、电流表达式为

在t4时刻之后，变换器将进入另外半个开关周期，并且原理类似，因此本文不再赘述。

1.3 电压增益

变换器的电压增益可以分为Boost 级和谐振级两个部分，即

根据Boost 电感（励磁电感）的伏秒平衡原则，Boost 级的电压增益可以表示为

对于谐振级，当谐振电流对谐振电容完成半个谐振周期的充电时，谐振电容电压会从最小值上升到最大值，因此谐振电容的最小值可以表示为

式中，ΔVCr为谐振电容电压峰峰值的一半；VCr_DC为谐振电容电压的直流偏置；Io为输出电流平均值。

将式（2）中谐振电流表达式中的vCr(t0)替换为VCr_min，可得

结合谐振电流与输出电流平均值的关系可得

同理，根据谐振电流负半周的表达式（4）可得

结合式（9）、式（10），谐振级电压增益关系可以推导为

因此，变换器的整体电压增益为

根据式（12），归一化的变换器电压增益曲线如图4 所示。可以看出，电压增益可以通过改变一次侧开关的占空比来调节。并且，在不同负载下，变换器的电压增益特性不变，该特性能够简化变换器的分析和设计。整体的电压增益特性和Boost 电路类似，因此所提出的变换器也可以视为隔离Boost变换器。

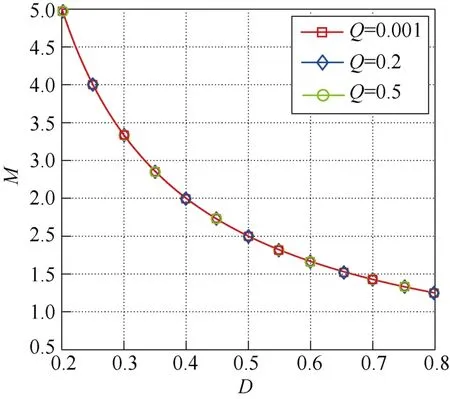
图4 电压增益曲线Fig.4 Voltage gain curves

1.4 ZVS 分析

在开关切换时刻，谐振电流等于零，因此开关的ZVS 仅依靠励磁电流实现。根据图3 中的工作波形，开关的ZVS 条件可以表示为

此外，励磁电流的直流偏置可以推导为

可以看出，因为一个开关周期内，谐振电流平均值等于0，因此励磁电流的平均值就等于输入电流平均值。对于式（13）中的 ZVS 条件来说，S2非常容易实现ZVS，在设计时只需要满足S1的ZVS条件，因该条件在重载下更难实现，因此需要保证变换器在满载的时候，励磁电流的纹波大于输入电流平均值的2 倍，即

式中，ILm_pp为励磁电流峰峰值；Ton为S1开通时间；Toff为S1关断时间。

由式（15）可以看出，在满载的条件下，设计合适的励磁电感值和开关频率，就可以实现全负载范围的ZVS。

2 无电流传感器的自适应频率控制

在轻载的时候，Boost 电感环流较大，因此可以通过提升开关频率来减小环流并优化电流纹波，但是由于在所提出的耦合电感集成拓扑中，Boost电感电流即励磁电流，无法直接测量得到，因此通过设计电流观测器来估计 Boost 电感电流的平均值，以此来计算得到最优的开关频率。

2.1 电流纹波优化

谐振电流和励磁电流纹波优化的过程如图5 所示。在负载较轻时，如果开关频率较低，变换器中将会存在较高的环流，导致导通损耗的占比较高，降低传输效率。在保证ZVS 的前提下，适当提高开关频率，可以有效减小谐振电流和励磁电流的纹波。

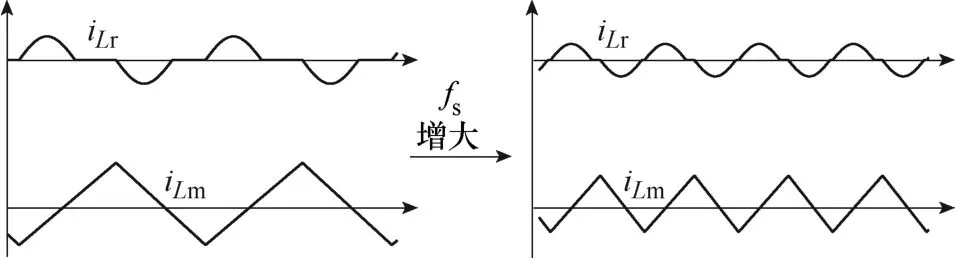
图5 提高开关频率后的波形Fig.5 Waveforms after increasing the switching frequency

根据式（15）中的ZVS 条件，开关频率上限值的计算需要知道输入、输出电压以及励磁电流平均值。然而，励磁电流无法直接通过传感器采样得到，因此可以通过设计励磁电流观测器来估计励磁电流平均值。

2.2 励磁电感电流观测器

CISRC 的等效电路如图6 所示，可以将谐振级等效为一个负载并联在励磁电感两端，电路的状态方程可以表示为

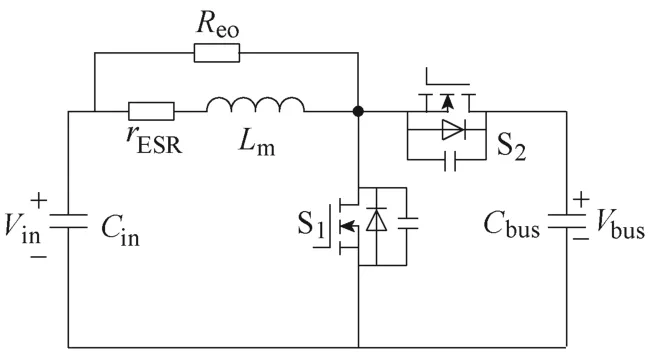
图6 CISRC 等效电路Fig.6 Equivalent circuit of CISRC

电路的观测器可以设计为

所设计的观测器的观测误差可以定义为

结合式（16）～式（18），观测误差的状态方程可以推导为

观测误差的动态必须是渐近稳定的，因此根据观测误差的定义构造李雅普诺夫函数为

式中，K3为观测系数。

李雅普诺夫函数是根据状态变量观测误差的能量定义的，因此，需要设计合适的观测器系数，使定义的观测误差的能量能够收敛至0。李雅普诺夫函数的导数可以推导为

根据式（21），为了保证函数V的导数小于或等于0，观测器的系数可以设计为

除了电感电流和母线电压的观测器状态方程，θ（包含等效负载）的观测状态方程可以由式（22）中的第三个等式推导得到，即

最终，励磁电流平均值观测器的方程设计为

根据式（24）绘制励磁电流观测器的框图如图7 所示。图中，励磁电感Lm、寄生电阻rESR以及中间母线电容Cbus为电路参数，通过输入电压Vin、母线电压Vbus以及占空比D，就可以得到励磁电流平均值的观测值。

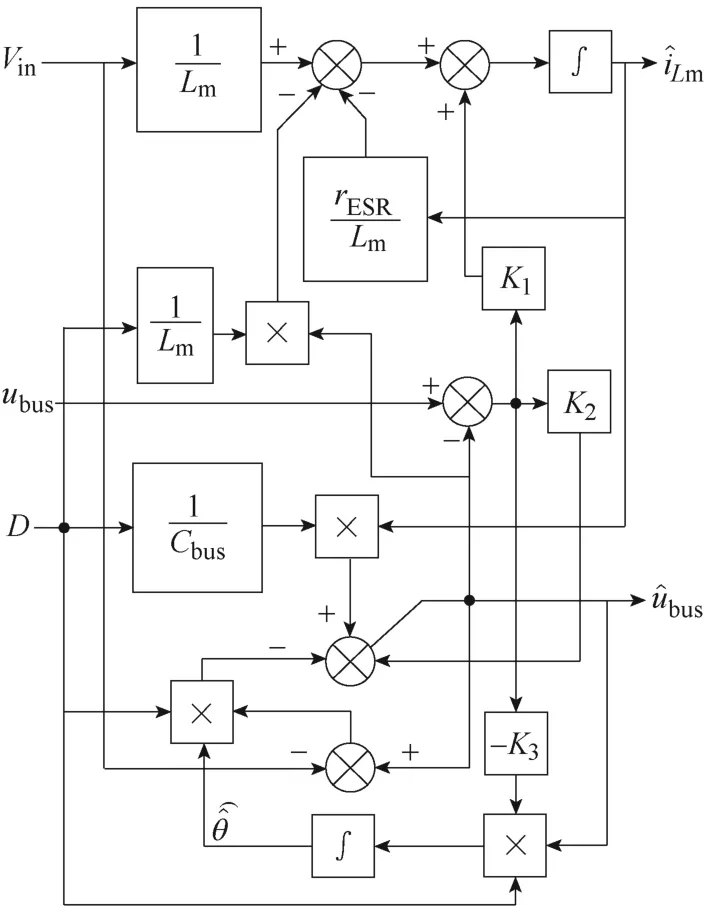
图7 励磁电流观测器框图Fig.7 Block diagram of excitation current observer

2.3 自适应频率控制

根据式（15）中的ZVS 条件，在当前输入电压和中间母线电压下，能够实现一次侧开关ZVS 的最高开关频率可以计算为

式中，输入功率Pin等于励磁电流平均值和输入电压的乘积。

另外，值得注意的是，为了保证谐振级能够实现单位电压增益以及与负载无关的增益特性，谐振电流需要完成半个周期的谐振过程，因此，开关管上管和下管的导通时间都应该大于谐振电流的半个谐振周期。那么开关频率、谐振频率以及开关占空比的约束条件可以表示为

式中，Tr、Ts分别为谐振、开关周期；fr、fs分别为谐振、开关频率。

根据2.1 节的分析，当开关频率较高时，输入电流纹波较小。因此最优的开关频率即为满足ZVS条件式（25）以及电压增益约束条件式（26）下的最高开关频率。本文所提出的自适应频率控制的流程如图8 所示。具体步骤为：

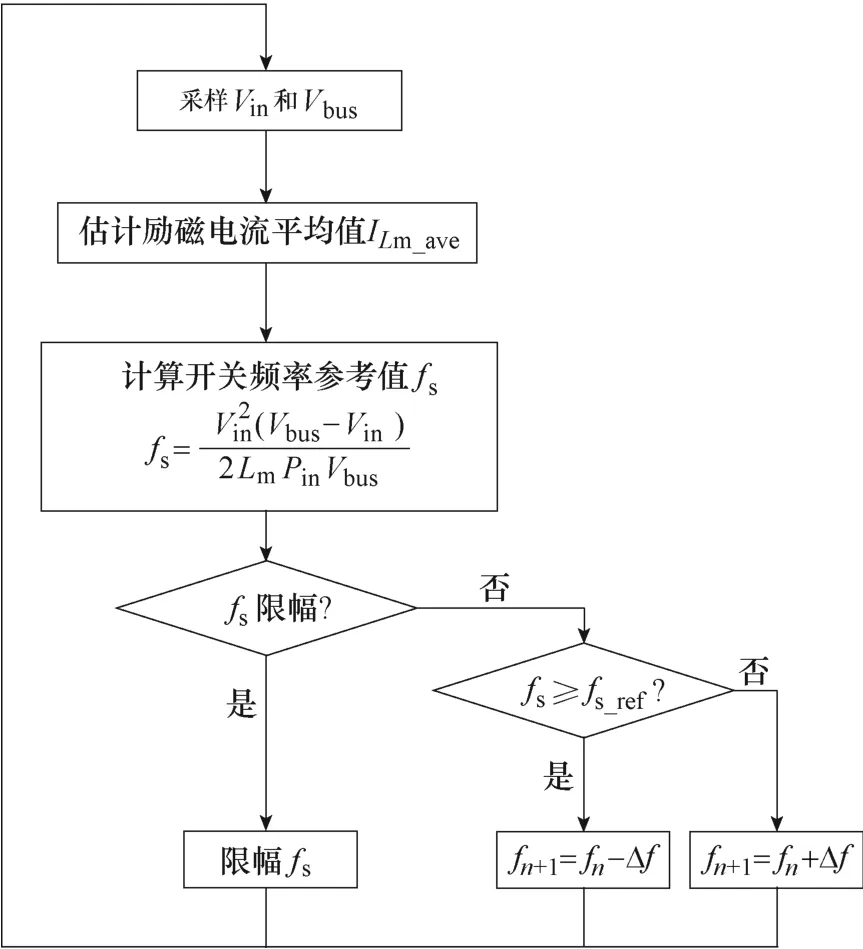
图8 自适应频率控制流程Fig.8 Flow chart of the proposed adaptive frequency control

（1）首先通过电压传感器采样，得到当前工作条件下输入电压Vin以及中间级直流母线Vbus的电压采样值。

（2）将采样得到的输入电压和中间直流母线电压代入所提出的励磁电感电流观测器，得到励磁电流平均值的估计值。

（3）根据式（25）中的ZVS 条件，计算得到当前工作条件下，能够实现一次侧开关管ZVS 的最高开关频率参考值。

（4）根据式（26）中的电压增益约束条件以及参数设计时的最低开关频率，得到开关频率的约束范围，并判断步骤（3）中的最高开关频率参考是否达到限幅，如果超出限幅的范围，则将开关频率参考修改为限幅值。

（5）将当前开关频率调整为优化后的开关频率参考值。

所提出的CISRC 的控制框图如图9 所示。本文采用了传统的单电压环PI 控制器控制输出电压。PI控制器的输入为电压参考值和输出电压采样值的差，并计算得到当前的占空比；同时根据所提出的基于励磁电流观测器的自适应频率控制，计算得到最优的开关频率；最后，控制芯片根据当前的占空比以及开关频率生成一次侧开关管S1与S2的PWM驱动信号。

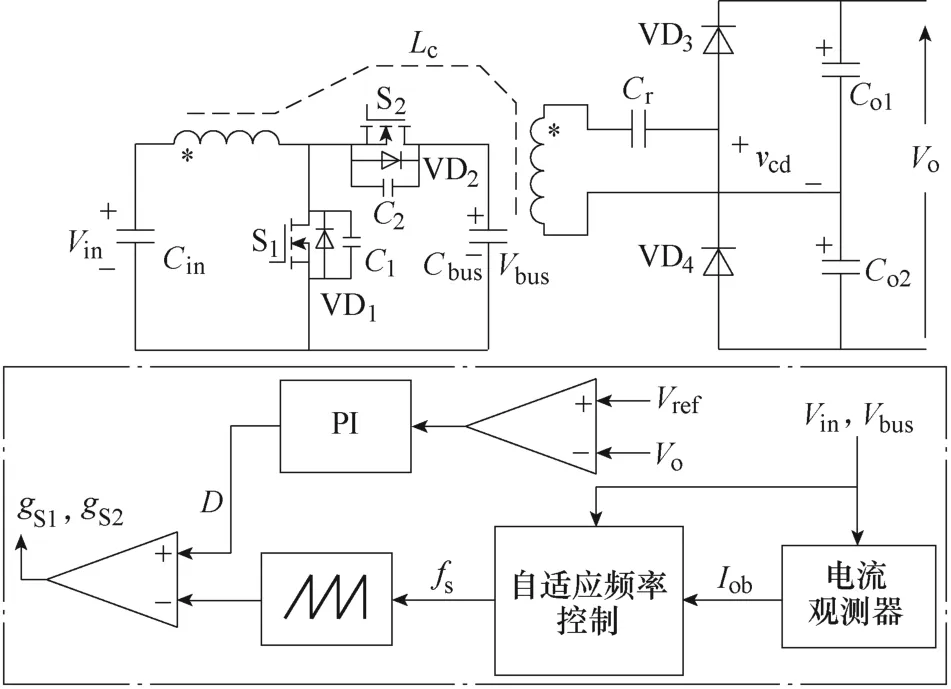
图9 控制框图Fig.9 Control block diagram

3 仿真与实验验证

本文以200 W 的样机为例，通过仿真和实验结果来验证所提出方案的可行性，样机参数见表1。

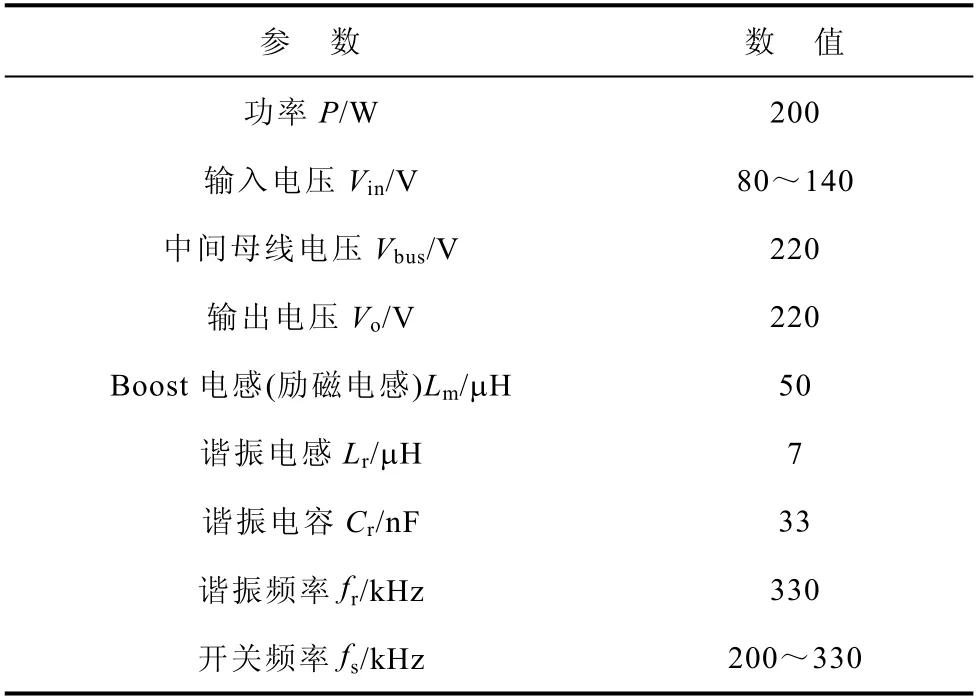
表1 样机参数Tab.1 The parameters of prototype

3.1 仿真结果

仿真波形如图10 所示。图中，iLm_ob为励磁电感电流平均值的观测值，可以看出，观测值和励磁电流的平均值基本相同，并且在负载切换时，也能快速的进入稳态。因此，所设计的励磁电流观测器是合理的，并且观测值可用于所提出的自适应频率控制。

图10a 和图10b 对比了采用自适应频率后的效果。图10a 中，没有采用自适应频率控制，当负载由满载切换至半载的时刻，由于开关频率较低且固定不变，那么在变换器工作在较轻的负载时，由于开关频率较低因而励磁电流的纹波较高，变换器中会产生较大的无功功率与环流；此外频率较低时，谐振电流的峰值也相对较高。因此，不采用自适应频率控制，在轻载下，变换器整体的电流纹波和导通损耗都较高。

图10 仿真波形Fig.10 Simulation waveforms

采用自适应频率控制后的仿真结果如图10b 所示。可以看出，当负载变轻时，在自适应频率控制的作用下，开关频率会相应提高到最优值，因此励磁电流和谐振电流的峰峰值都会减小。提高到最优开关频率后，励磁电流依然含有一定的负值能够实现一次侧开关的ZVS，并且输出电压依然可以保持恒定。在动态切换的时刻，当开关频率调整时，励磁电感电流和输出电压的波动不大，在短时间内能快速恢复稳态。

由对比结果可以看出，采用自适应频率控制能够有效地优化电流纹波。

3.2 实验结果

变换器在 80、110 和 140 V 输入下的满载（200 W）稳态实验结果如图11 所示。可以看出，在不同输入电压下，调节相应开关管的占空比来控制输出电压。在所设计的输入电压范围内，谐振电流始终能够完成半个周期的谐振，并且其波形为正弦半波，满足谐振级的单位电压增益约束条件式（26）。另外，由于输入电压不同，励磁电流的平均值也不同，根据式（25）和式（26）可知，不同输入点下的开关频率最优值也不同，因此在所提出的自适应频率控制的作用下，变换器的开关频率也会得到相应调节。

图11 满载稳态实验结果Fig.11 Steady state experimental results under full load

此外，因为一次侧桥臂的下管 S1更难实现ZVS，因此实验结果中给出了开关S1的ZVS 波形。可以看出，在开关管S1开通前，开关管的漏源极电压已经提前降低至0，那么实验结果可以说明开关实现了软开关。此外，在不同输入电压下，开关管S1都可以保证实现ZVS。变换器轻载（10 %负载）的稳态实验结果如图12 所示，在轻载条件下，由于励磁电流的平均值较小，反向电流较高，更容易实现ZVS。因此，所提出的变换器能够在整个电压范围内实现全负载ZVS。

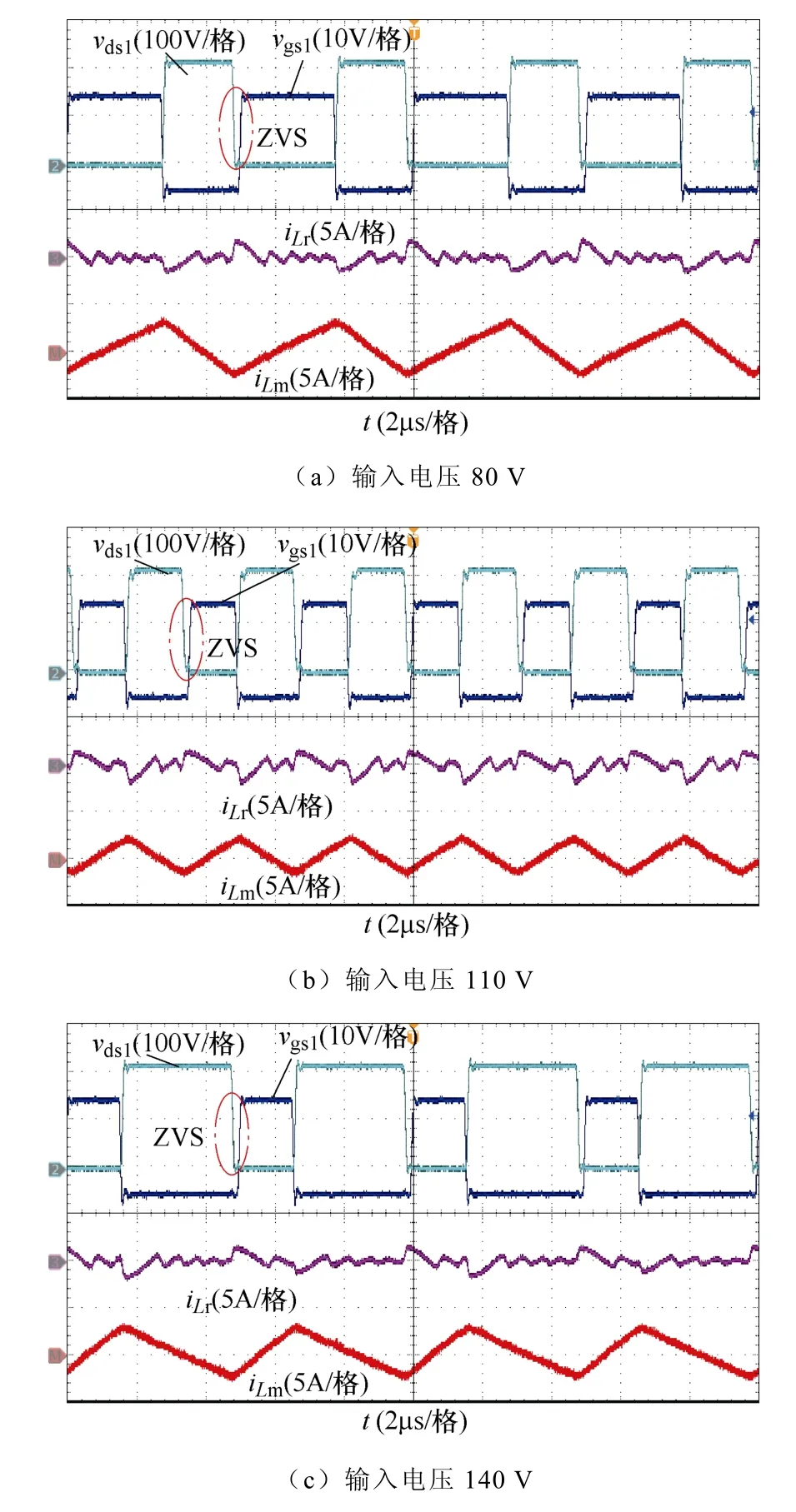
图12 轻载（10 %负载）稳态实验结果Fig.12 Steady state experimental results under light load

动态切换的实验对比结果如图13 所示。图13a没有采用自适应频率控制，因此开关频率固定，当负载从重载切换至半载后，谐振电流和励磁电流的峰峰值依然较高。采用自适应频率控制的切换实验结果如图13b 所示，当负载变轻后，开关频率也随之提升，谐振电流和励磁电流的纹波均有效减小。尽管在切换过程中，输出电压和励磁电流有一定的波动，但是变换器能够快速进入稳态。因此，采用所提出的自适应频率控制能够有效优化电流纹波。

图13 动态实验对比结果Fig.13 Dynamic experimental results

测量效率与电压增益如图14 所示。当输入电压较高时，工作电流较低，因此转换效率较高。此外，变换器在半载左右时转换效率较高，随功率和工作电流的增加，转换效率也会有所下降。由于开关死区和器件导通压降的影响，变换器测量的电压增益曲线和理论计算的增益曲线存在一定误差，但是误差较小，实验结果基本和理论分析相符。

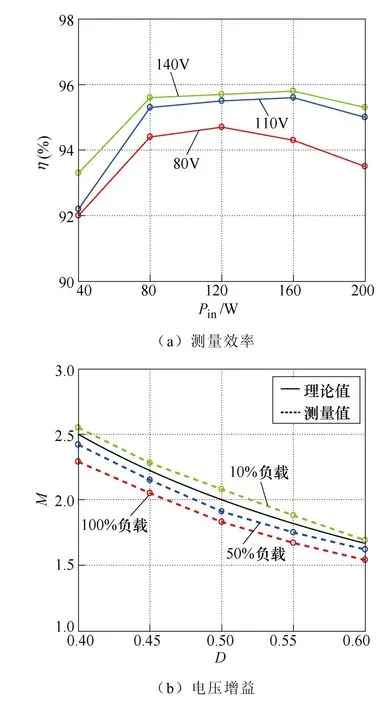
图14 测量效率与电压增益Fig.14 Measurement efficiency and voltage gain

4 结论

本文提出并研究了一种耦合电感集成型的谐振变换器，所提出的变换器通过一个耦合电感集成了Boost 电路和串联谐振电路。集成后开关管的数量有效减少，而耦合电感替代了Boost 电感，谐振电感以及高频变压器，进一步减少了磁性元件。一次侧MOS 管能够实现ZVS，二次侧二极管能够实现ZCS。此外，为了优化电流纹波，提出了一种无电流传感器的自适应频率控制。其中由于励磁电流无法直接通过传感器测量得到，因此设计了励磁电感电流观测器来估计得到励磁电流的平均值。最后，通过仿真和实验结果验证了所提方法的正确性与可行性。