面向舰船综合电力系统的10 kV/2 MW 模块化多电平双向直流变换器控制策略

刘计龙 陈 鹏,2 肖 飞 朱志超 黄兆捷

（1.海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430033 2.东南大学电气工程学院 南京 210096）

0 引言

舰船综合电力系统是发展海上舰船的突破性技术，其以电能作为统一的形式实现了全船能量的生产、输运、变换、消纳和存储。1998 年马伟明院士创新科研团队率先提出发展基于中压直流系统的二代舰船综合电力系统（Integrated Power System,IPS）技术路线。与传统的中压交流系统相比，中压直流系统功率密度更高、可靠性更好、功率控制更灵活、振动噪声更小[1-3]。

中压直流系统和储能元件的引入是二代舰船IPS 的显著特征。因此，二代舰船IPS 对变配电变换器提出了新的需求：①有更高的耐电压能力，可以承受中压直流母线的接入；②有双向功率变换能力，可以实现中压侧与低压侧的双向能量交互；③模块化水平高，便于生产、制造与维护；④有较高的功率密度和运行效率，节省船上空间，可大大加强船只的续航能力。

目前在舰船直流配电领域研究最多的两种中高压拓扑是基于模块化多电平变换器（Modular Multilevel Converter,MMC）的端对端结构[4-8]和模块化多电平双向直流变换器（Modular Multilevel Bidirectional DC-DC Converter,MMBDC）结构[9-11]。后者也可称为基于 MMC 的输入串联输出并联（Input Series Output Parallel,ISOP）结构。文献[7,12]比较了这两种拓扑形式的优缺点并指出，基于MMC 的端对端结构由于基本单元形式更加简单，冗余保护成本更低，容错运行也更简单。而与之相比，MMBDC 结构更加紧凑，功率密度更高，器件的电气应力也更低。考虑到舰船可利用空间非常有限，本文主要针对MMBDC 结构开展研究。

目前已有较多关于MMBDC 的文献发表，文献提出了在直流多端口MMC 后级级联不同类型的拓扑，如双有源桥（Dual Active Bridge,DAB）等，来构成MMBDC 结构[9-11,13-15]，也有部分文献在MMC后级并联多个低压两端口子变换器或低压多端口子变换器来构成中高压多端口MMBDC 结构[16-18]。上述文献所采用的MMBDC 拓扑结构与主要研究内容见表1。可以看出，MMBDC 在直流配电领域拥有出色的应用潜力。

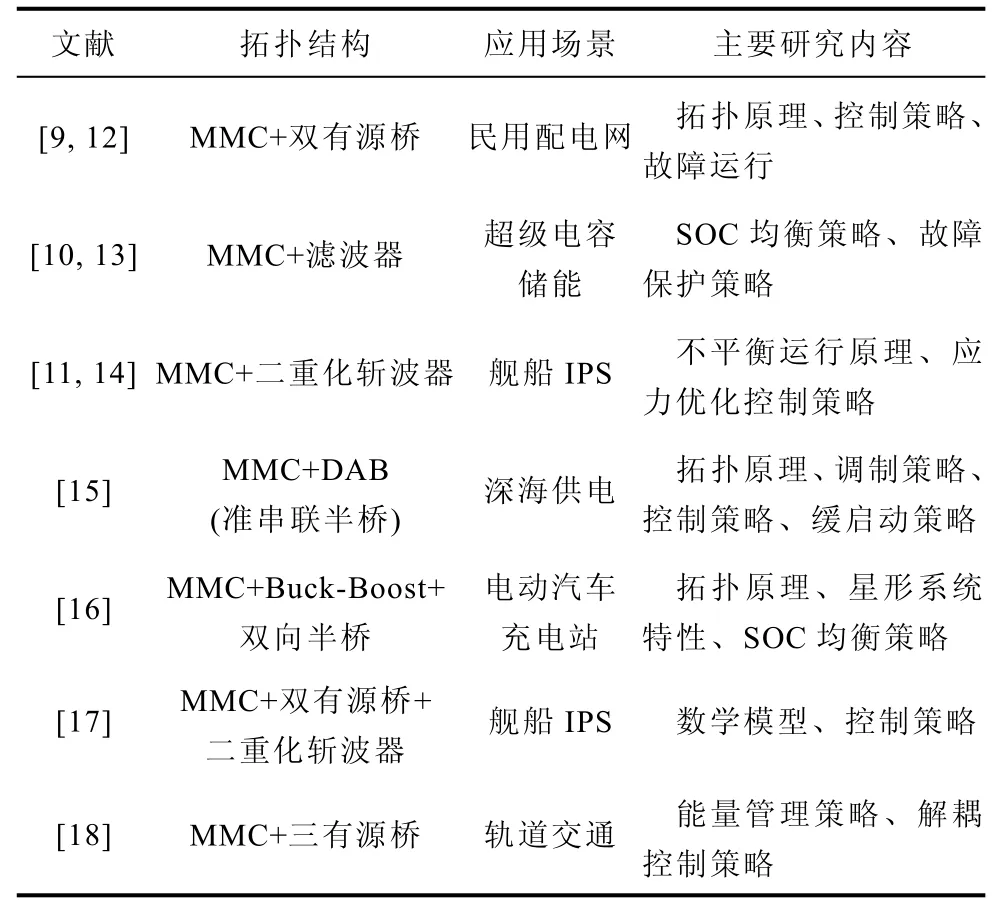
表1 MMBDC 文献综述Tab.1 Literature overview of MMBDC

文献[9]针对MMBDC 的直流多端口MMC 子变换器提出一种平均电压环与均压环相结合的三环控制策略，使得变换器能够在额定工况下稳定运行。然而，该策略控制变量采样难、未直接控制中压侧电流、环路耦合强，且未考虑中压侧低频振荡问题。这些劣势在中高压大功率应用中尤为明显。

对此，本文为直流多端口MMC 子变换器提出一种改进的三环解耦控制策略，该策略以中压侧电流作为平均电压环内环控制量，便于对其进行限幅，防止中压侧过电流；通过陷波器抑制了中压侧电感与子模块开关电容之间的低频振荡；实现了平均电压环与均压环的解耦。另一方面，针对低压侧连接储能元件时DAB 的低频谐振问题，本文提出了基于陷波器的双向功率控制策略。此外，本文设计并制作了10 kV/2 MW 级MMBDC 工程样机，通过满功率实验验证了所提出的控制策略的有效性。

本文所提出的控制策略加强了MMBDC 的稳定性与可靠性，提高了装置的控制性能，也简化了控制参数设计过程。此外，本文的实验平台的设计可为其他同类型的中压大功率电力电子变换装置的设计和实现提供参考依据。

1 MMBDC 拓扑原理

1.1 基本拓扑

由N条支路构成的MMBDC 如图1 所示，每条支路由MMC 子变换器的半桥子模块（Half Bridge Sub-Module,HBSM）和DAB 子变换器级联而成。

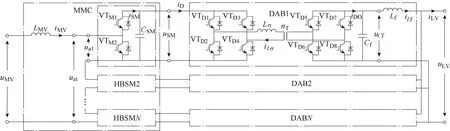
图1 MMBDC 结构Fig.1 Topology of MMBDC

MMBDC 的硬件电路参数包括：支路数N、中压侧滤波电感LMV、子模块电容CSM、变压器电压比nT、低压侧滤波电容Cf、低压侧滤波电感Lf。本文假设这些参数在各支路中是一致的。

MMBDC 的电气参数包括：中压侧电压uMV、中压侧电流iMV、子模块电压uSM、半桥子模块斩波电流iSM、DAB 一次侧输入电流iD、变压器一次侧漏感电流iLσ、低压侧滤波电容电压uCf、低压侧滤波电感电流iLf、低压侧电压uLV和低压侧总输出电流iLV。VTM1和VTM2分别为MMC 半桥子模块的上管和下管IGBT，VTD1～VTD8为DAB 子变换器的IGBT。

与普通ISOP 结构相比，MMBDC 用直流多端口MMC 替代了输入串联结构，为后级提供了多路可调的直流电源。两种子变换器MMC 和DAB 通过子模块电容解耦，二者控制策略可以分开设计。

在直流配电应用中，MMBDC 有如下优势：

（1）MMC 和DAB 子变换器均为双向变换器，因此无论在中压侧或低压侧连接的是有源负载还是无源负载，MMBDC 都可以完成功率的双向灵活传输。

（2）MMC 子变换器提供了不平衡运行能力[11]。因此可以在MMBDC 低压侧连接分布式储能元件或无源负载，使MMBDC 运行在各支路功率不平衡的工况下。

（3）当部分支路发生故障时，可以持续导通对应子模块的下管IGBT 以及辅助旁路开关即可将故障支路切除，而不影响其余支路的正常运行。

（4）MMBDC 避免了在中压侧采用集中式大电容，减小了中压侧短路电流冲击，子模块电容中存储的电量也有利于故障后的快速重投[9]。

（5）MMC 子模块电容可调，因此，可以使得DAB 始终运行在一次、二次电压匹配的工况下，提高了运行效率。

MMC 子变换器采用移相调制策略[9,11]，可以起到等效倍频的效果，大大降低了中压侧电流纹波。由于子模块电压可调，一次、二次电压匹配程度较好，DAB 子变换器采用单移相调制策略[19]。

1.2 数学模型

若忽略中压侧电感电流纹波和子模块电容电压纹波，可以建立MMC 子变换器状态平均方程为

若采用均压控制，认为各子模块电压和占空比一致，并忽略中压侧电感内阻，有

式（3）即为中压侧电流与子模块电压的函数关系。

设各支路占空比、负载电流及子模块电压的稳态值均相同，对式（1）分离小信号得到

式中，带有上标“*”的变量为对应信号的稳态量；iDi为MMC 子模块负载电流扰动。MMC 小信号状态空间方程见附录第1 节。

以半桥子模块占空比到中压侧电流的开环传递函数GMDI为例进行分析，忽略中压侧电感内阻，GMDI表达式为

本文设计了10 kV/2 MW 级MMBDC 工程样机的参数见表2（详见3.1 节）。将表2 所示参数代入式（5）可知，特征方程的阻尼比很小，因此可以认为谐振频率和无阻尼自然振荡频率近似一致，其表达式为

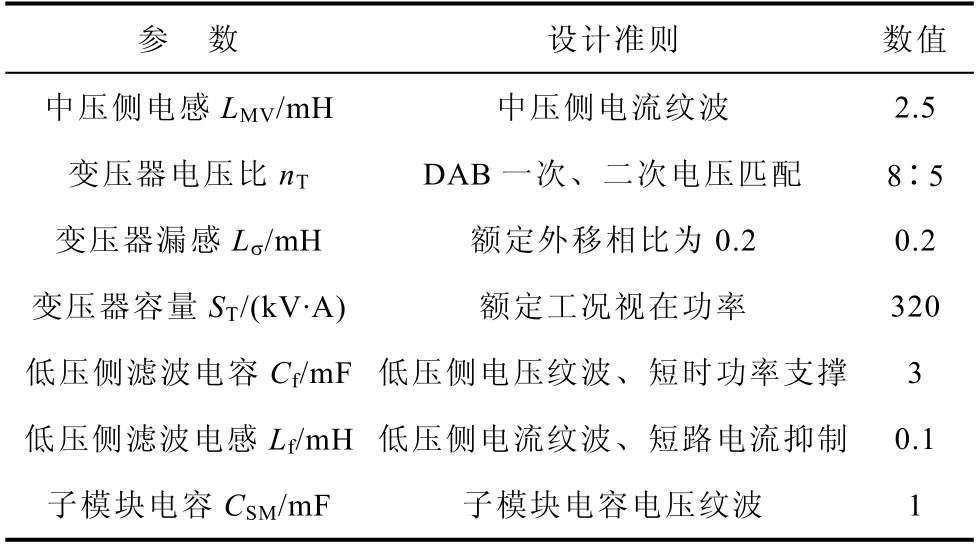
表2 MMBDC 硬件参数设计准则及数值Tab.2 Design criteria and designed values of hardware parameters of MMBDC

以GMDI为例对本文所建立的数学模型进行仿真验证。在任意一个半桥子模块占空比上叠加1 Hz～2 kHz 的正弦扰动，并在中压侧电流处提取相应频率的扰动分量，计算出仿真测量的传递函数，同样代入表2 所示参数，得到GMDI伯德图仿真证明如图2 所示。可以看出，GMDI在222 Hz 附近有一个谐振峰，且全频段仿真结果与所建立的数学模型符合度较高，说明了数学模型的准确性。

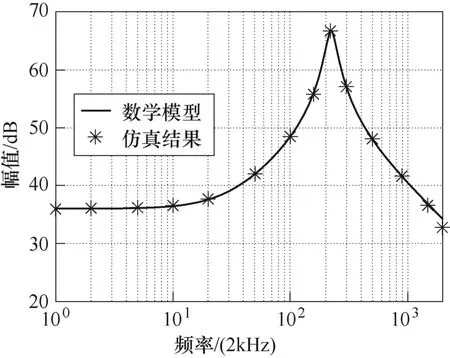
图2 GMDI 伯德图仿真证明Fig.2 Simulation verification of GMDI Bode diagram

DAB 传统的建模方法为降阶模型，该种模型计算简单，但忽略了漏感电流这一状态变量，导致模型精度存在较大偏差，在中高频段偏差尤为明显。对此，研究者提出采用广义平均模型对DAB 进行建模[20-22]。DAB 的广义平均模型引入了漏感电流的基波分量，提高了DAB 模型精度。

当低压侧连接无源负载时，DAB 状态方程为

式中，s1和s2分别为DAB 一次、二次侧H 桥的开关函数。当VTD1和VTD4导通时，s1=1；当VTD2和VTD3导通时，s1=-1；当VTD5和VTD8导通时，s2=1；当VTD6和VTD7导通时，s2=-1。RD为单个DAB 等效电阻负载。带上标“＇”的变量均为归算到变压器一次侧的值。

DAB 漏感电流可以视为纯交流分量，低压侧滤波电容电压和滤波电感电流可以视为纯直流分量，式（7）写成广义平均模型形式为

设DAB 的控制输出为输入电流iD、输出电流iLf和输出电压uLV，将这三个变量均视为直流量，则其输出方程的广义平均模型为

将式（8）和式（9）代入广义平均模型的换算公式[20-21]，并分离小信号即可得到DAB 的小信号广义平均模型状态空间方程。具体推导如附录第2 节所示。

本文以外移相比到低压侧漏感电流的传递函数GDDIL为例进行了仿真证明，结果如图3 所示。可以看出，仿真结果与理论模型在全频段一致性较好，验证了所建立数学模型的准确性。

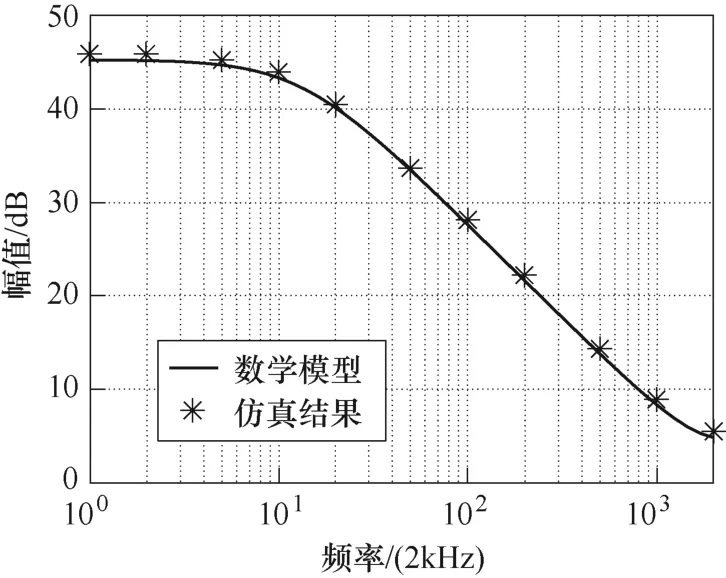
图3 GDUIL 伯德图仿真证明Fig.3 Simulation verification of GDUIL Bode diagram

低压侧连接有源负载时，DAB 的数学模型的推导方法与低压侧连接无源负载时相似，推导过程不再赘述。图4 为低压侧连接有源负载时DAB 外移相比到低压侧滤波电感电流的传递函数GD＇DIL的仿真证明结果。可以看出，理论曲线与仿真证明结果在全频段吻合度较高，验证了数学模型的准确性。

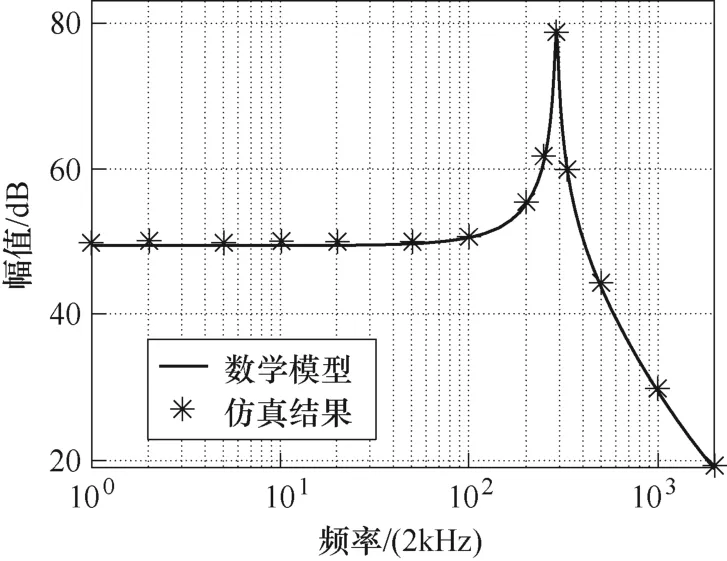
图4 GD＇DIL伯德图仿真证明Fig.4 Simulation verification of GD＇DIL Bode diagram

比较图3 和图4 也可以发现，当DAB 低压侧连接有源负载时，外移相比到低压侧滤波电感电流的传递函数存在一个谐振峰，其谐振频率即为低压侧滤波电容和低压侧滤波电感产生的LC 串联谐振频率，表达式为

2 MMBDC 控制策略

2.1 MMC 传统控制策略

传统的直流多端口MMC 子变换器控制策略框图如图5 所示[9]。其由通过各子模块共用的平均电压外环、独立的均压外环以及独立的输出电流内环组成。

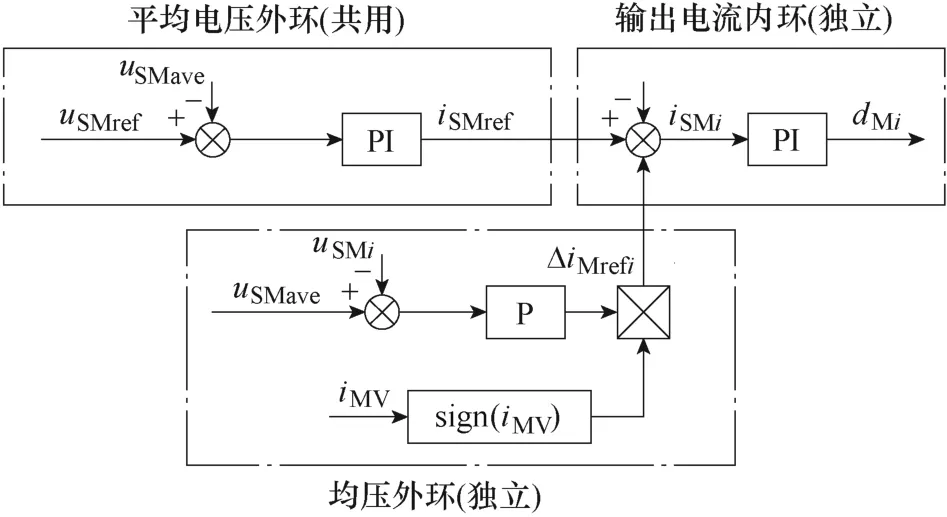
图5 MMC 传统控制策略Fig.5 Traditional control strategy of MMC

图5 中，PI 表示比例积分调节器，P 表示比例调节器，sign()表示取符号函数。传统控制策略使变换器稳定运行在额定工作点，但也存在如下缺陷：①由于子模块输出端没有感性元件，iSMi纹波较大，采样较难；②平均电压环与均压环存在耦合，控制参数设计较难；③中压侧电流不受控，存在过电流风险；④未考虑直流多端口MMC 固有的低频振荡问题。将图5 所示的控制策略应用于中高压大功率应用时，这些问题更为明显。

2.2 MMC 基于陷波器的三环解耦控制策略

针对上述传统控制策略存在的问题，本文针对直流多端口MMC 子变换器提出了一种基于陷波器的三环控制策略如图6 所示。图中，NF 表示陷波器。上述策略采用中压侧电感电流iMV作为平均电压环的内环控制变量。平均电压外环产生中压侧电流内环的给定iMVref，通过陷波器抑制式（6）所示的低频谐振点，然后经过PI 调节器后产生子模块共用的占空比dMC。均压环的PI 输出乘以中压侧电流方向Sign(iMV)后产生占空比的补偿量ΔdMi，然后将dMC与ΔdMi作差得到各子模块的下管占空比dMi。在所提出的控制策略中，前N-1 个子模块的占空比补偿量由PI 调节器算出，而最后第N个子模块的占空比补偿为0 减去其余子模块占空比补偿量之和，即

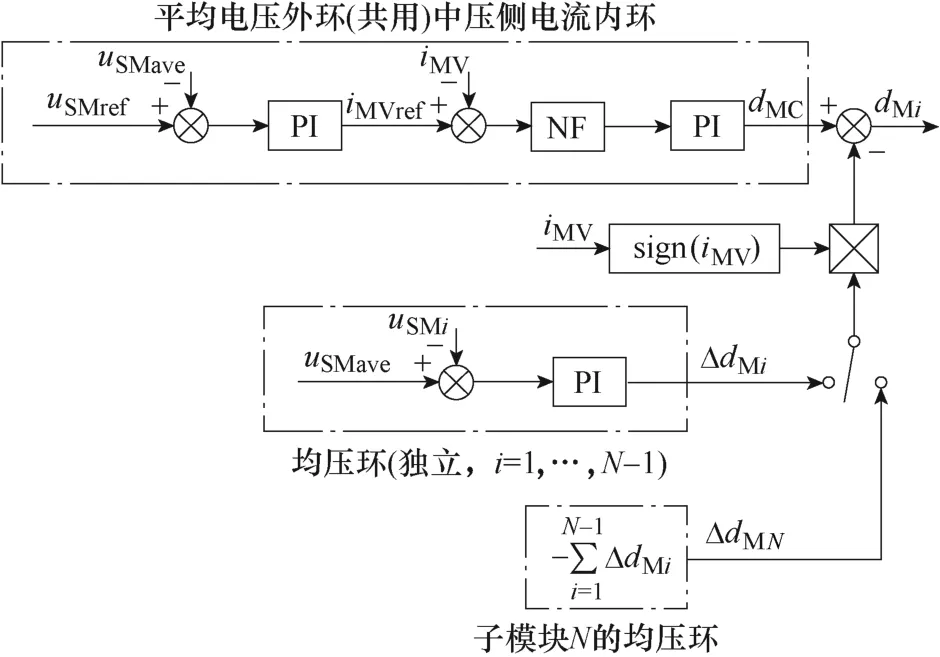
图6 MMC 改进控制策略Fig.6 Advanced control strategy of MMC

以中压侧电流正向流动为例，中压侧电流反向流动时分析方法与之相同。首先根据MMC 数学模型，可以得到关系式为

又根据图6 得到

结合式（12）和式（13）有

对式（14）进行小信号分离，并假设各子模块占空比和子模块电容电压的稳态值分别一致，可以推得

从式（15）可以看出，若在设计均压环时令式（13）成立，即所有均压环的输出之和为0，那么中压侧电流和子模块电压之和（或平均值）仅受到平均电压环的共用占空比扰动以及中压侧电压扰动影响。换言之，平均电压环不受均压环的影响。这样在实际应用中就可以首先对平均电压环设计控制参数，然后在此基础上对均压环进行控制参数设计。需要说明的是，上述控制策略仅保证了平均电压环不受均压环的影响，但无法保证均压环不受平均电压环的影响。

从图6 可以看出，所提出的控制策略为了实现均压环的解耦，破坏了各子模块控制策略的对称性，可以进一步对其进行简化。设前N-1 个子模块的PI调节器传递函数为GPI_MUB，由图6 所示策略得到

式（16）表明，第N个子模块的均压环和前N-1 个子模块是一致的，因此，图6 可以简化为如图7 所示的简化MMC 改进控制策略。

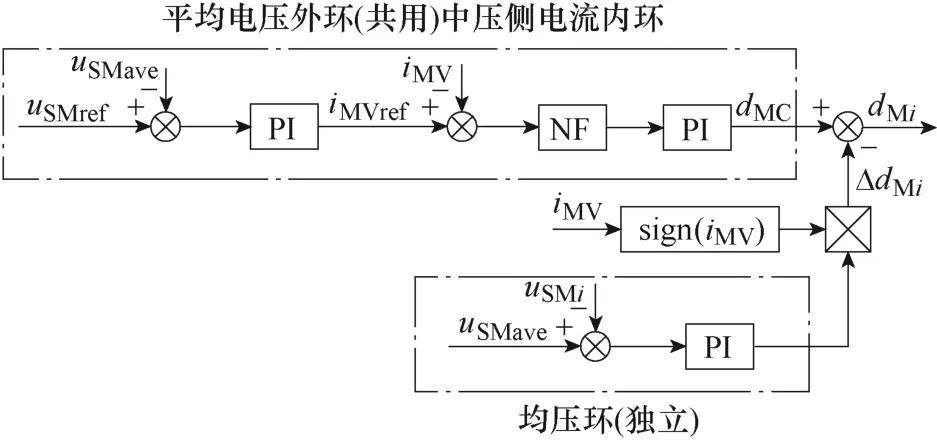
图7 简化MMC 改进控制策略Fig.7 Simplified advanced control strategy of MMC

2.3 MMC 控制策略对比

2.2 节中提到，所提出的基于陷波器的MMC 三环解耦控制策略可以抑制低频谐振。在传统控制策略中，由于未引入陷波器，为了保证控制系统稳定性，需要牺牲动态响应速度；而所提控制策略通过引入陷波器解决了该矛盾。下面进行具体量化分析。

根据图5 和图7 可以推导出传统控制策略下和所提控制策略下电流内环的开环传递函数为

式中，TMI为电流内环PI 调节器传递函数；GMNF为所提控制策略的陷波器传递函数，其表达式分别为

式中，kNF为陷波系数；ωrMI为陷波角频率。

对式（17）中两个开环传递函数代入表2 参数，在传统控制策略下选择PI 参数（kpi=0.000 1，kii=0.2），在所提控制策略下选择PI 参数（kpi=0.002，kii=4），得到传统策略与所提策略伯德图对比如图8所示。可以看出，在所设计的PI 参数下，传统控制策略与所提控制策略在222 Hz 谐振点附近的幅值均为0 dB 左右。二者相位裕度分别是94.3 °和95.2 °，差异不大。但所提控制策略的截止频率（206 Hz）远大于传统策略的截止频率（7.97 Hz）。此现象表明，所提控制策略由于引入了陷波器，以中压侧电流为控制目标的内电流环的环路设计带宽远大于传统控制策略的带宽，大大加快了变换器的动态响应速度。

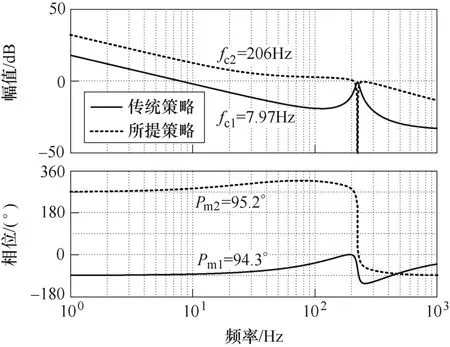
图8 传统策略与所提策略伯德图对比Fig.8 Comparison between the Bode diagrams of the traditional strategy and the proposed strategy

2.4 DAB 基于陷波器的双向功率控制策略

由于各支路差异较小，本文在DAB 中采用共外移相比控制策略。

当低压侧连接无源负载时，采用双闭环控制策略，外环控制低压直流母线电压，内环控制各支路平均输出电流。带无源负载时DAB 控制策略如图9所示。具体而言，首先将低压侧电压参考uLVref与实际值uLV作差，经过PI 调节器后产生低压侧总输出电流iLVref参考。将总输出电流参考iLVref均分到各条支路形成DAB 输出电流参考iLfref，再与各支路输出电流平均值iLfmean作差，经过PI 调节器后产生共用的外移相比dD。上述双闭环控制策略是各支路共用的。

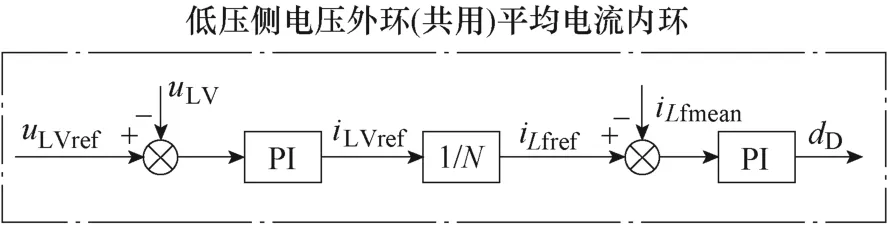
图9 带无源负载时DAB 控制策略Fig.9 Control strategy of DAB with passive load

低压侧连接有源负载，如超级电容或蓄电池，由DAB 控制低压侧端口电流。式（10）展示了在此工况下存在的LC 低频谐振问题。对此，本文在电流控制环路中引入陷波器对其进行抑制，控制策略框图如图10 所示。

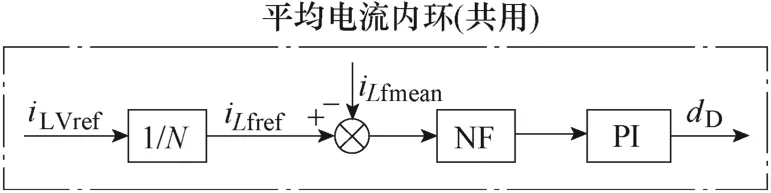
图10 带有源负载时DAB 控制策略Fig.10 Control strategy of DAB with active load

3 MMBDC 样机设计与实验

3.1 硬件参数设计

本文设计硬件参数的输入条件为：中压直流母线电压uMV=10 kV，低压直流母线电压uLV=1 kV，装置额定总功率ptot=2 MW。结合参数设计的输入条件和现有IGBT 器件的水平，本文选择额定电压为3 300 V 的IGBT 作为MMBDC 中压侧（包括MMC 和DAB 一次侧）的开关器件，并设计工作电压为1 600 V。为了实现中压侧电感LMV的伏秒平衡，MMBDC 的支路数量和子模块电容电压必须满足以下约束

根据式（19）所示的约束，MMBDC 的最小支路数为7，本文将支路数取值为N=8。

由于MMC 不具备软开关特性，而DAB 由于一次电压可调，可以始终运行在软开关运行范围内，开关损耗较低，因此，MMC 开关频率设计值应低于DAB 开关频率设计值。经过损耗计算和热仿真验证，本文将MMC 开关频率fM设计为2 kHz，将DAB 开关频率fD设计为4 kHz。其余硬件参数的设计准则及数值见表2。

3.2 绝缘设计

MMBDC 中压侧直流母线电压高达10 kV，超出了常用的低压电气元件的绝缘等级，为器件选型、电气柜机械结构设计带来了挑战。本文在进行绝缘设计时主要有以下几点考虑。

（1）各支路连接在中压侧的功率单元（包括MMC 的开关器件、DAB 一次侧的开关器件、吸收电容、子模块电容、复合母排、水冷板等元器件）均分别固定在同一金属支撑架上。该金属支撑架即为各支路中压侧浮地，金属支撑架通过绝缘材料与外机壳相连。浮地设计示意图如附录第3 节所示。

（2）各支路子模块电容电压、变压器漏感电流、MMC 与DAB 一次侧的功率单元温度，均通过各支路独立的中压侧控制箱进行采样，功率单元温度通过温度变送器采样。

（3）各支路中压侧元器件供电的辅助电源模块应通过独立的隔离变压器与220 V 交流输入进行安全隔离。

（4）各支路中压侧控制箱、辅助电源以及相应的隔离变压器的外壳直接连接到各支路的中压侧浮地上。中压侧辅助供电模块的各路输出的模拟地以及子模块电容负极通过20 kΩ 绝缘电阻连接到浮地上。

3.3 控制系统架构

10 kV 超出了常规控制器的采样电路和调理电路的耐压等级。为了保证控制器的安全，各支路中压侧和低压侧的电气量应采用不同的控制器分开采样。对此，本文针对MMBDC 提出了“一主十从”的环网控制架构，MMBDC 控制系统架构如图 11所示。

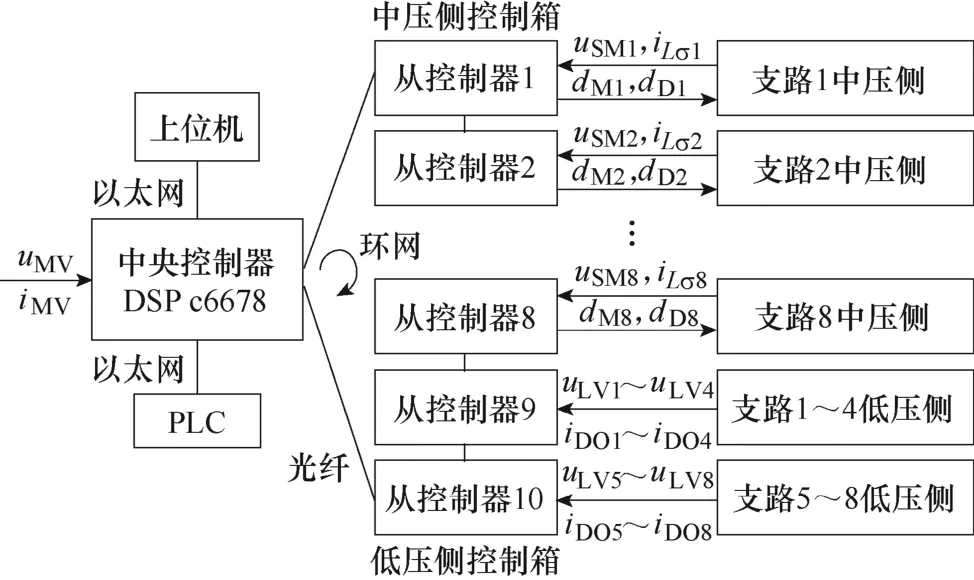
图11 MMBDC 控制系统架构Fig.11 Control system architecture of MMBDC

在图11 所示的“一主十从”控制架构中，主控制器和每个从控制器均设置了独立的FPGA 来进行环网通信和电气量的采集。所有采样的电气量通过环网传递到中央控制器的FPGA 中去，再通过UDP传输到 DSP。所有的控制算法均通过主控制器的DSP 来实现。DSP 再将计算结果通过环网下发到从控制器的FPGA 中去产生PWM。

如图11 所示，主控制器负责采样10 kV 侧的电气量，包括中压侧电压和中压侧电流。从控制器1～8 分别负责对应支路的子模块电容电压、漏感电流、中压侧IGBT 温度等变量的采样。低压侧电气量包括低压侧电压和低压侧电流均由从控制器9 和10来进行采样。第i条支路的所有驱动信号，均由第i个从控制器的FPGA 发出，以降低环网通信延迟。

MMBDC 包含的子变换器较多，控制算法较为复杂。为了加快算法执行速度，选择TMS320C6678作为主控芯片，通过以太网和PLC 以及上位机进行通信。用户可以用上位机实时观测DSP 数据，也可以下发机械开关动作指令或进行在线调参。PLC 负责控制MMBDC 样机中的机械开关。

3.4 电气柜结构布局

MMBDC 样机实物及俯视图如图12 和图13 所示。

图12 MMBDC 样机实物Fig.12 Photo of MMBDC prototype

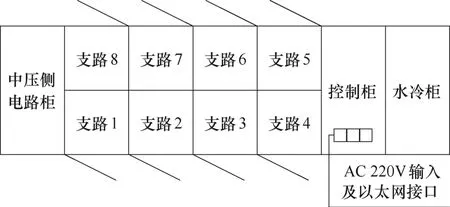
图13 MMBDC 样机俯视图Fig.13 Vertical view of MMBDC prototype

从图12 和图13 可以看出，MMBDC 工程样机由11 个电气柜构成：中压侧电路柜、控制柜、水冷柜及8 个支路柜。每个电气柜的构成及功能如下。

（1）中压侧电路柜为MMBDC 提供连接中压直流母线的接口以及保护和检测元件。其包含熔断器、预充电电路、中压侧支撑电容、中压侧电感以及对应的霍尔器件。

（2）8 个支路柜分别对应8 条支路，采用模块化设计，每个支路柜元器件及结构布局完全相同。8个支路柜“背靠背”布置，便于检修维护。每个支路柜分成4 层：第1 层装设中压侧控制箱以及辅助电源模块；第2 层为中压侧IGBT 功率单元；第3层为中频变压器；第4 层为低压侧IGBT 功率单元。本文考虑到磁粉芯的高频特性较好，将其作为中频变压器的铁心材料。

（3）主控制器、低压侧从控制器9 和10、PLC以及以太网光纤交换机都集成在控制柜中。

（4）MMBDC 主要器件均采用水冷的散热方式。水冷柜额定功率为 84 kW，内水额定流速为305 L/min，采用去离子水来保证安全隔离。此外，每个支路柜柜门上还设计了风扇来实现柜体内外空气流通。

3.5 实验结果

首先对 MMBDC 进行了静态实验。中压连接10 kV 直流电源，低压侧电阻负载包括满载0.5 Ω和轻载0.937 5Ω 两种。子模块电压给定为1 600 V，低压侧电压给定分别为800、900 和1 000 V。满载和轻载工况下的稳态实验数据见表3。本文所采用的中压直流电源是由民用交流配电网通过不控整流产生的，受到配电网实时负荷的影响，所以不能刚好保持在10 kV 上。

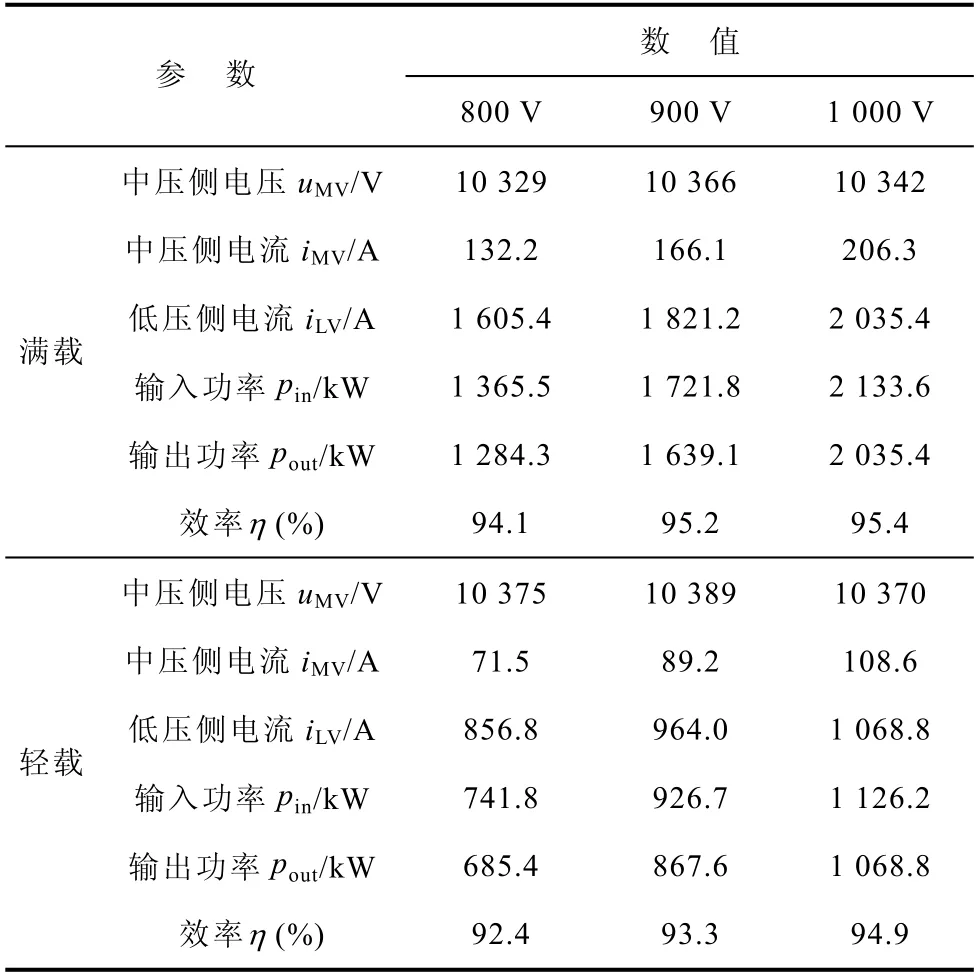
表3 MMBDC 稳态实验结果Tab.3 Steady-state experiment results of MMBDC

低压直流母线电压、输出功率标幺值以及运行效率的关系如图14 所示。从图14 可以看出，满载工况下MMBDC 的运行效率都在95 %以上，满足电力电子变换器对效率的一般要求[23-25]。总体上看，MMBDC 输出功率越大，效率越高。

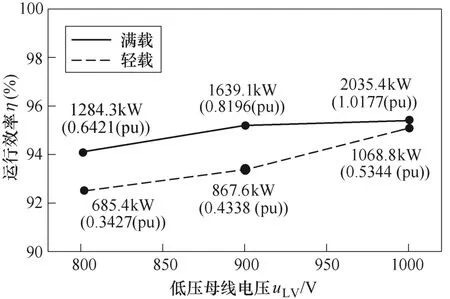
图14 不同低压侧电压下的稳态实验结果Fig.14 Steady-state experimental results under different LVDC voltage

图15 为MMBDC 在额定功率2 MW 下运行的稳态实验波形，实验数据由上位机采集。从图 15可以看出，MMBDC 可以稳定运行，各子模块电容电压均衡，低压侧输出电流一致性较好，低压侧输出电压纹波仅为额定值的0.49 %。

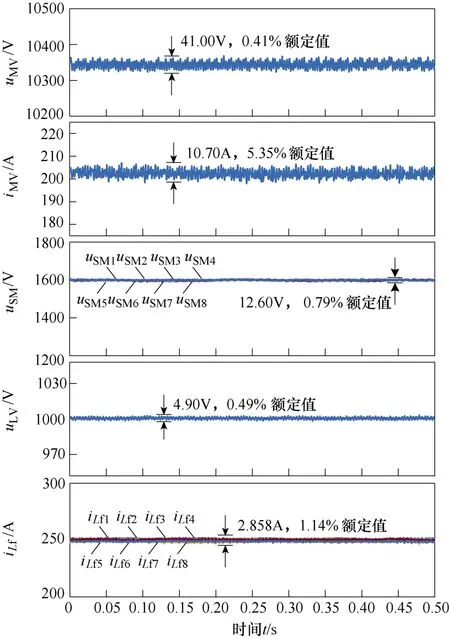
图15 MMBDC 在额定工况下的稳态实验波形Fig.15 Steady-state experimental waveforms of MMBDC under rated working condition

本文为了抑制起动电流，采用了扩展移相调制。但本文DAB 一次、二次电压匹配程度较高，因此，扩展移相调制与单移相调制的稳态波形很接近。DAB 子变换器的实验波形如图16 所示。从实验波形可以看出，DAB 一次电压为1 600 V，二次电压为 1 000 V，二者的比值与中频变压器电压比 8∶5一致。尽管实际情况下由于元器件参数和采样的偏差，一次、二次电压并不能完全匹配，但也能保证DAB 软开关、中频变压器漏感电流呈梯形波。

图16 DAB 实验波形Fig.16 Experimental waveforms of DAB

本文进行了MMBDC 动态加载卸载实验。将低压侧电压给定和子模块电容电压给定分别设置为1 000 V和1 600 V，将负载电阻通过断路器从0.937 5Ω 切换至0.5 Ω 的动态加载实验波形如图17 所示。

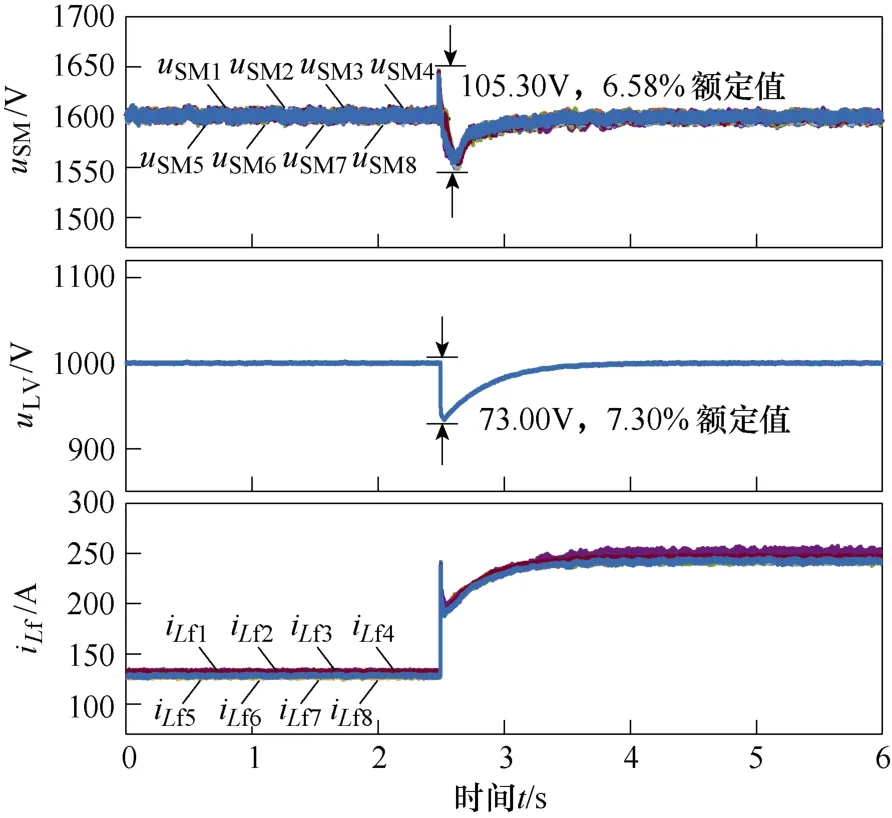
图17 动态加载实验波形Fig.17 Transient experimental waveforms of loading

由图17 可以看出，突加负载时，子模块电容电压波动为105.30 V，占额定值的6.58 %。低压侧电压波形为7.30 V，占额定值的7.30 %。动态调节过程为0.35 s。

将负载电阻从0.5 Ω 切回0.937 5 Ω，可以得到动态卸载实验波形如图18 所示。此时子模块电压波动为74.50 V，占额定值的4.66 %。低压侧电压波动为99.50 V，占额定值的9.95 %。整个动态卸载的调节过程约为0.4 s。

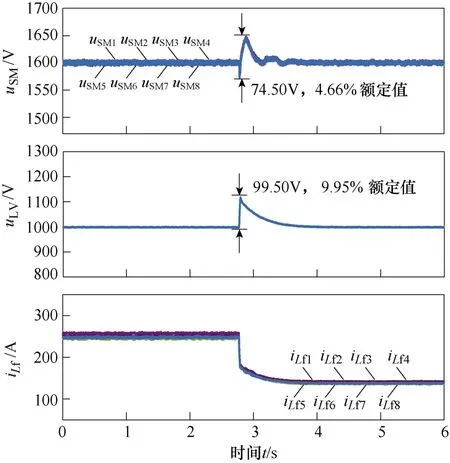
图18 动态卸载实验波形Fig.18 Transient experimental waveforms of unloading

以上实验结果表明，所设计的MMBDC 工程样机在所提出的控制策略下呈现出较好的动静态性能，说明了设计方法和控制策略的有效性。

为了验证MMBDC 在所提控制策略下的双向功率传输特性，本文在低压侧连接了集中式超级电容，并进行了双向功率传输实验验证。超级电容柜实物如图19 所示。整个集中式超级电容由2 个超级电容柜组成，单个超级电容柜的参数见表4。

表4 单个超级电容柜参数Tab.4 Parameters of a single supercapacitor cabinet

图19 超级电容柜实物Fig.19 Photo of the supercapacitor cabinets

根据超级电容的充放电特性，本文采用一种“慢充快放”的恒流充放电控制策略，并设计了如下验证实验。首先对超级电容进行充电，充电电流给定为160 A，当超级电容电压达到1 050 V 时，将电流给定改变为0；然后再改为-1 000 A，进入放电模式。当超级电容放电至850 V 时，再将电流指定置零，并切换为160 A，重新进入充电模式，如此往复。图20 为MMBDC 双向功率控制实验波形。可以看出，在所提出的控制策略下，MMBDC 的双向功率控制有较好的动静态特性。

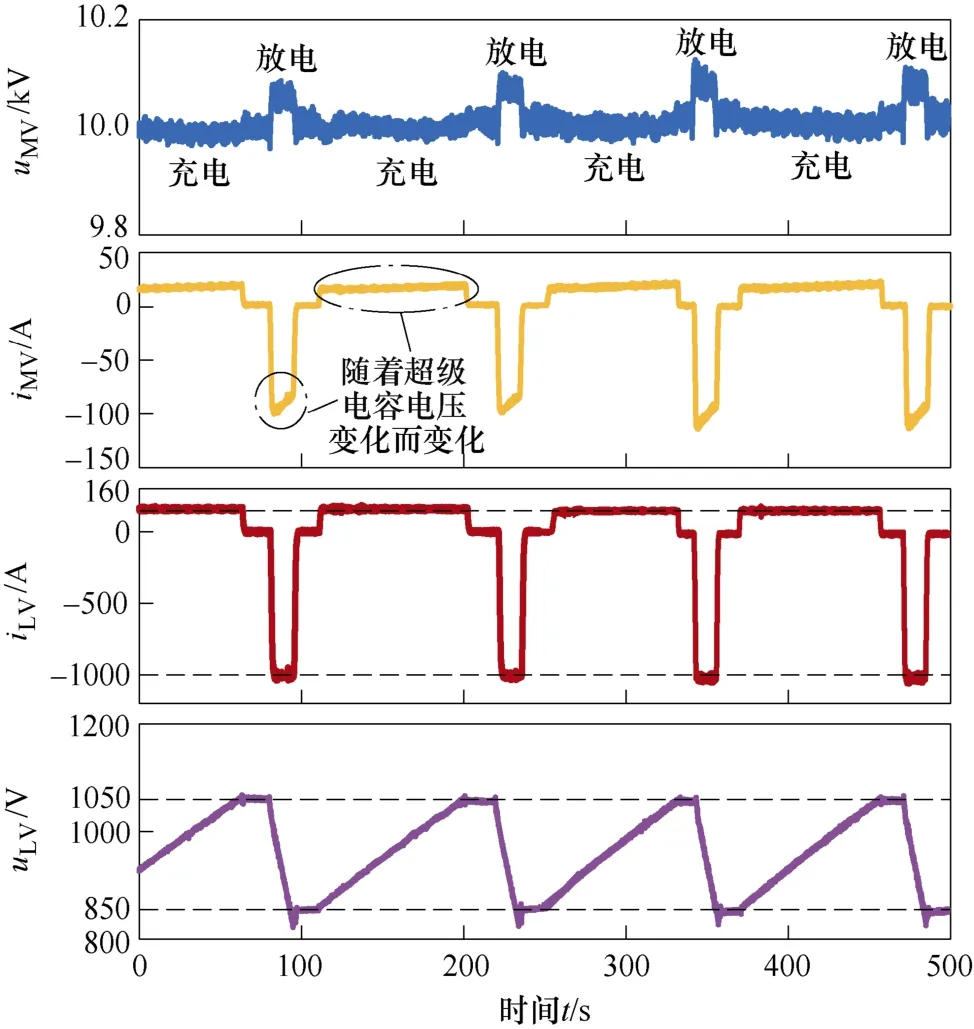
图20 MMBDC 双向功率控制实验波形Fig.20 Experimental waveforms of bidirectional power control of MMBDC

4 结论

为了满足新一代舰船综合电力系统实际需求，本文对MMBDC 控制策略开展研究，主要结论如下。

1）分析了MMBDC 拓扑原理，发现其存在中压侧电感与各支路开关电容串联谐振的问题，谐振频率如式（6）所示。

2）针对直流多端口MMC 子变换器提出了一种基于陷波器的三环解耦控制策略。与传统策略相比，所提控制策略采用中压侧电流作为内环控制量，方便了反馈信号采样；使得中压侧电流可控，规避了中压侧过电流风险；实现了均压环与平均电压环的解耦，简化了控制参数设计；在环路中引入了陷波器，通过对低频谐振点的抑制，将内电流环带宽从7.97 Hz 提高至206 Hz。

3）本文设计并制造了10 kV/2 MW 的MMBDC工程样机。介绍了该样机的绝缘设计、控制系统架构以及电气柜结构布局，并进行了所提控制策略的动静态实验。静态实验结果表明，在本文所提控制策略下，变换器满载额定工况效率可达95.4 %，低压侧电压纹波仅为额定值的0.49 %；动态加减载实验表明，在所提控制策略下进行47 %额定负荷加减载时，最大子模块电容电压波动为额定值的6.58 %，最大低压侧电压波动为额定值的9.95 %，动态调节过程不超过0.4 s。动静态实验结果说明了所提控制策略的有效性。

4）本文研究也可以说明，MMBDC 在MW 级工程应用中的可行性，可为其他中压变换器的设计和制造提供参考。

此外，为了对所提控制策略进行实验验证，本文设计并制造了10 kV/2 MW 的MMBDC 工程样机。介绍了该样机的绝缘设计、控制系统架构以及电气柜结构布局，并给出了所提控制策略的动静态实验结果，验证所提策略的有效性。

附 录

1.MMC 小信号模型

式（4）变换到频域并写成矩阵形式为

式中，各项元素的表达式如式（A2）所示。

由式（A1）得到

式中，GMO为MMC 的开环传递函数矩阵。由于不考虑移相角，根据对称性，各占空比到对应子模块电压的传递函数GMDUC相同，各占空比到非对应子模块电压的传递函数GMDUN相同，各占空比到中压侧电流的传递函数GMDI相同。各负载电流到对应子模块电压的传递函数GMIUC相同，各负载电流到非对应子模块电压的传递函数GMIUN相同，各负载电流到中压侧电流的传递函数GMII相同。

因此，GMO只包含八种传递函数（上述六种传递函数，外加中压侧电压到中压侧电流的传递函数GMUI和中压侧电压到子模块电压的传递函数GMUU），整体如式（A4）所示。

2.DAB 小信号模型

当DAB 低压侧连接电阻负载时，根据式（8）和式（9）可以列出DAB 广义平均模型如式（A5）和式（A6）所示。

式中，上标“R、I”分别表示该系数的实部和虚部，上标“*”表示变量的平均值。

3.绝缘设计示意图

MMBDC 绝缘设计如附图1 所示。

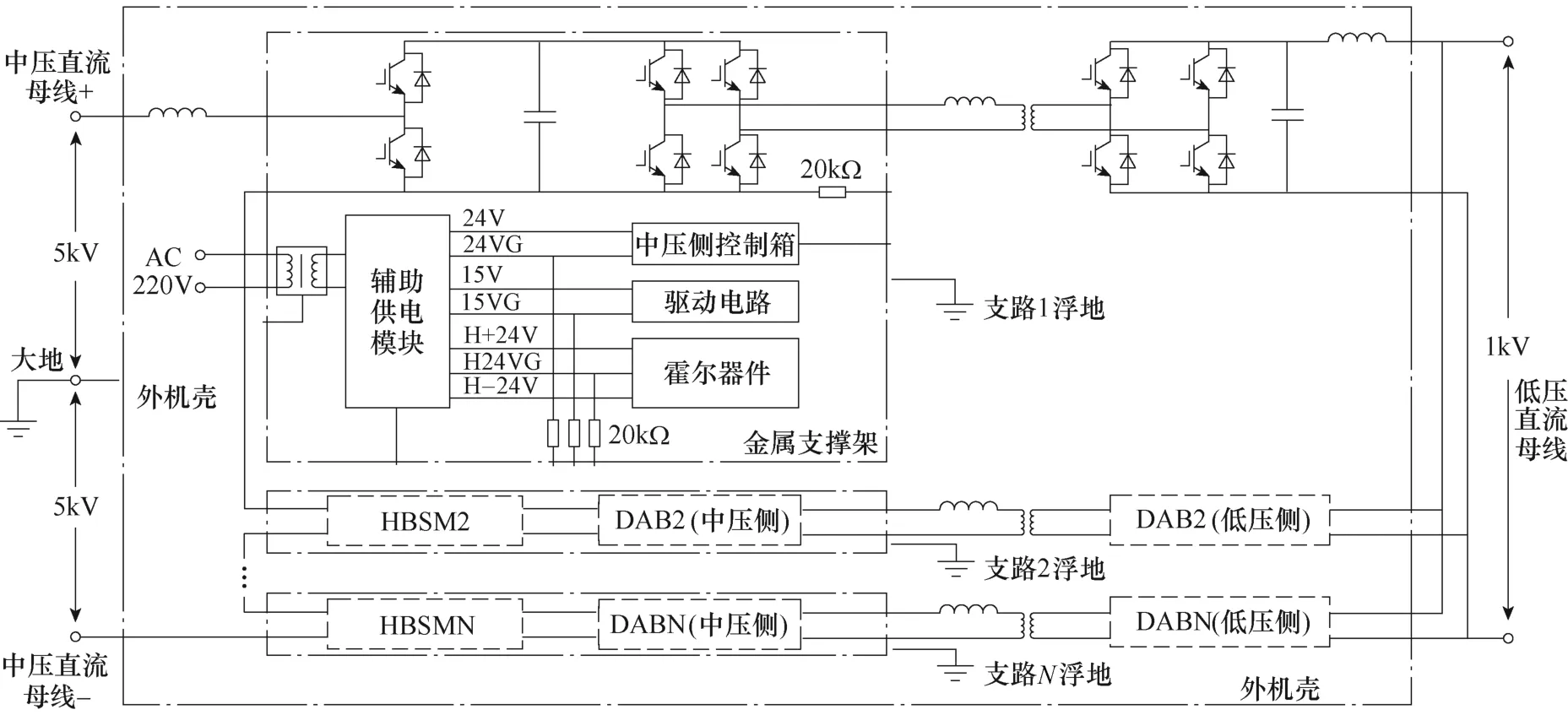
附图1 MMBDC 绝缘设计App.Fig.1 Insulation design of MMBDC