基于FEM/Kriging 近似模型结合进化算法的表贴式高速永磁电机转子强度优化

李 玮 汪泽润 张凤阁

（沈阳工业大学电气工程学院 沈阳 110870）

0 引言

近年来，由于高速永磁电机具有体积小、功率密度高、效率高、可与高速负载直接相连、省去传统的机械增速装置、减小系统噪声等优势[1]，在高速负载及分布式发电系统等领域广泛使用，具有广阔的发展前景[2]。大功率的高速永磁电机多采用表贴式转子结构，永磁体轴向及周向分块布置，磁极间填充非磁性材料，同时为满足高速运行的强度要求护套一般选用碳纤维材料[3-4]。由于高速永磁电机的转子强度要求较高，找到一种可高效优化转子强度的方法是亟待解决的问题，首选方式是对转子及永磁体等几何结构参数进行合理调整，充分提升转子机械强度，但对于复杂结构的有限元模型（Finite Element Model,FEM）往往需要数十次乃至数百次的迭代计算才能得出优化方案，这样将极大地影响电机的研发过程。

目前国内外研究者针对表贴式高速永磁电机转子强度开展了许多研究工作。王继强等[5]基于厚壁筒理论计算了合金护套不同工况的转子强度解析表达式，得到过盈量、护套厚度与转子应力的关系。在此基础上，陈亮亮等[6]采用解析法推导出各向异性碳纤维护套多工况下永磁转子应力分布情况，并与有限元方法计算进行验证，所得结果相一致。永磁体转子的极间填充材料能保证转子结构的整体性并起到阻尼作用，因此有学者开展了永磁体转子的极间填充材料属性对转子强度影响的相关研究[7-8]。王天煜等[9-10]研究了多物理场耦合情况下转子强度，考虑了温度场梯度变化对转子应力的影响，并采用方差分析的方法对转子结构强度进行了敏感性分析。刘威等[11]建立了包括轴间填充物的转子结构模型，研究了轴间填充物对转子强度的影响。张晓祥等[12]考虑软磁复合材料抗拉强度的局限性，研究碳纤维保护套下转子损耗特性，并进行转子结构强度分析，为新型混合励磁电机结构优化奠定了基础。

国内外研究者针对电机优化问题也开展了相关研究，杜方鑫等[13]针对高速永磁电机设计中转子强度的结构参数优化问题，建立了关于护套厚度和过盈量的参数化有限元模型。以遗传算法为主程序，调用参数化有限元程序计算得到的最大应力和接触力结果作为适应度评价函数，得出了满足强度要求的最小护套厚度和过盈量。黄振峰等[14]结合正交试验和Isight 集成优化平台，建立了质量匹配和振动特性的多目标优化模型，采用响应面函数（Response Surface Methodology,RSM）近似模型和带精英策略的非支配排序遗传算法（elitist Non-dominated Sorting Genetic Algorithm,NSGA-Ⅱ）求解，提升了电机轴系设计的可靠性和高速运转的稳定性。一些学者采用Kriging 近似模型方法优化电机，包括对双馈感应发电机（Doubly-Fed Induction Generator,DFIG）最大输出功率进行优化[15]，以及对飞轮储能电机进行了气隙磁通密度波形优化[16]等。目前在电机优化中常选取的优化方法包括近似模型法、有限元优化法和智能算法（以遗传算法为代表）等[17-18]。近似模型法以响应面模型和Kriging 模型为代表，缺点是模型精度取决于样本数量，需要大量采样来保证计算精度；有限元法能满足计算精度要求，但对复杂问题的计算成本大、耗时较长。

基于上述电机优化研究成果，本文以1.12 MW、18 000 r/min 的表贴式高速永磁电机转子为优化对象，建立其参数化几何模型，采用有限元法分析方法计算电机转子的应力场分布。将护套厚度、永磁体厚度、过盈量及工况温度设置为优化变量，以永磁体、护套的径向及切向应力最大值尽可能小为优化目标，从而达到提升高速永磁电机转子强度的目的。结合目前普遍使用的优化方法具体设计两种典型的技术路线并作对比分析：技术路线一，采用进化算法（Evolutionary Algorithm,EA）与FEM 结合进行优化设计，利用EA 算法采用多种参数组合并调用FEM 进行优化迭代计算；技术路线二，通过拉丁超立方抽样法选取优化参数，并利用有限元模型求出对应的永磁体应力及护套应力的最大值作为输出参数，构成样本空间，对样本空间进行拟合得到用于替代传统FEM 求解器的Kriging 近似模型，基于近似模型，结合EA 算法，进行优化设计过程。

1 计算模型

1.1 几何建模及应力场计算

本文以三维转子结构进行有限元应力场计算，建立的几何模型及横截面如图1 所示，包括五个部分：转子铁心、隔磁块、分块永磁体、胶层和护套。转子铁心外径178.2 mm，护套厚度3 mm，永磁体厚度20 mm，胶层厚度0.2 mm，转子铁心直径132 mm。各部分材料特性参数见表1。其中，隔磁件采用不锈钢材料，护套采用复合碳纤维材料。

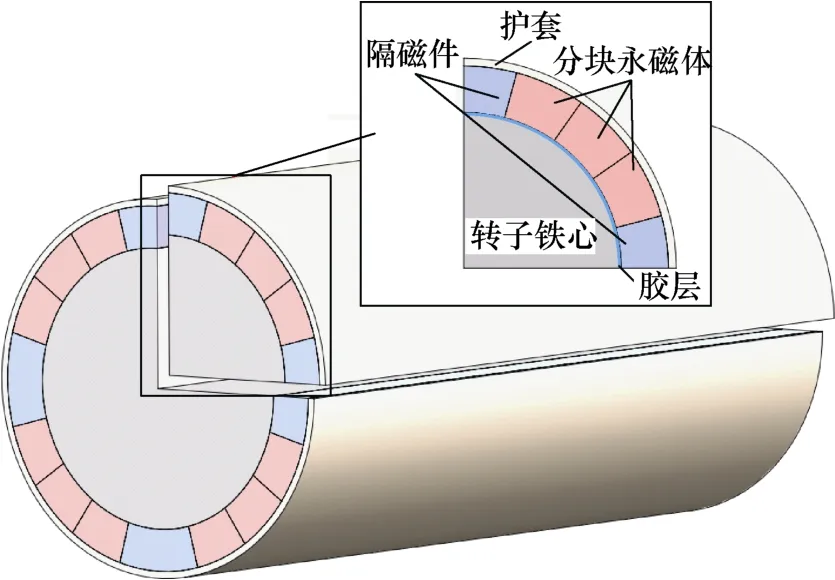
图1 表贴式高速永磁电机转子结构Fig.1 Rotor structure drawing of surface attached high speed permanent magnet motor

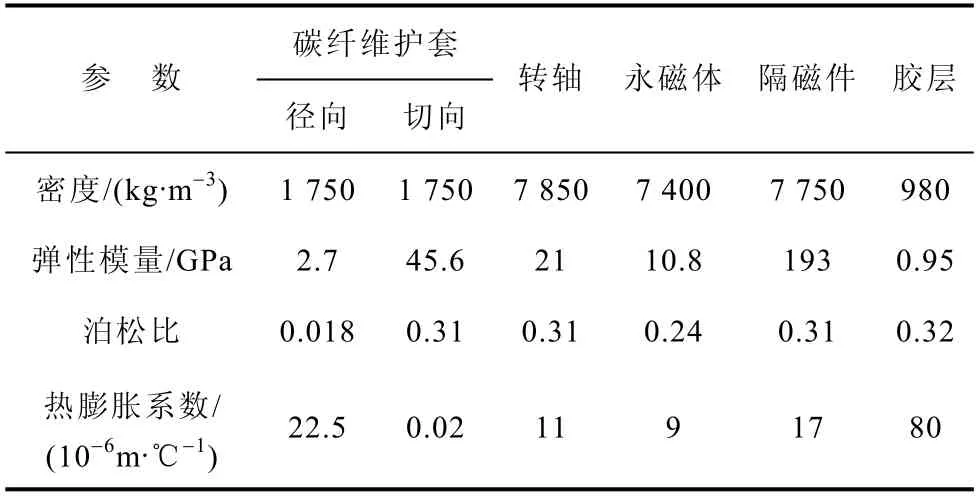
表1 材料特性参数Tab.1 Material characteristic parameter

由于转子是对称结构，为简化有限元计算步骤，利用 1/4 转子的结构模型建立应力场仿真计算模型，并在不影响计算准确性的前提下简化转子的一些细节部分。护套与永磁体和隔磁件之间为过盈配合，过盈量为0.01 mm，永磁体和隔磁件通过胶层粘结在转子铁心外表面，设置胶层两侧部件界面为粘接约束，其他相接界面设为摩擦约束。由于护套、永磁体、转子铁心及隔磁件的热膨胀系数不同，各组件所产生的热应力不同，利用3D 有限元法对表贴式高速永磁电机转子在温度150 ℃、转速18 000 r/min情况下的受力情况进行分析，得到的应力场分布如图2 所示。

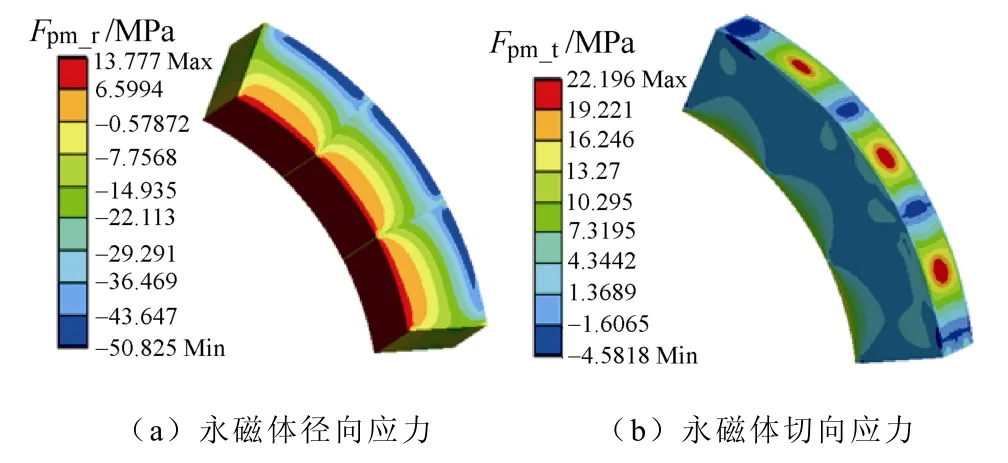
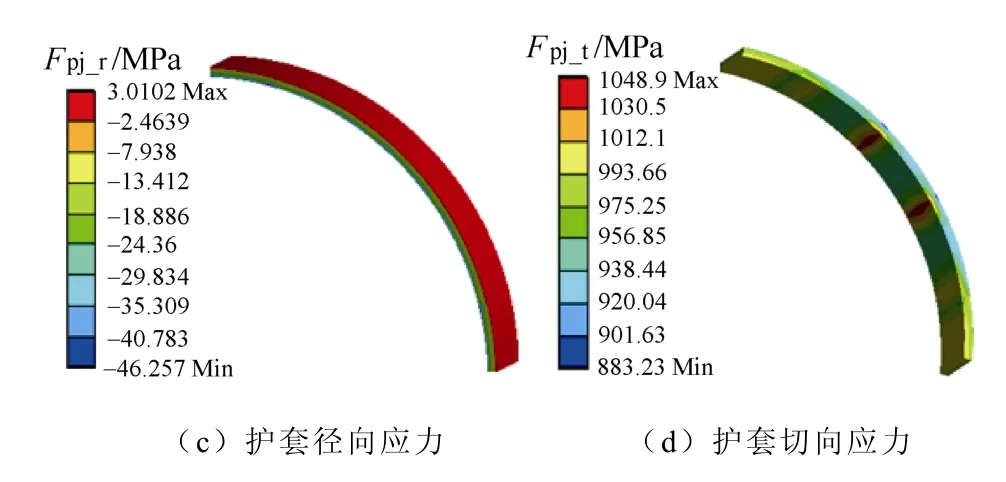
图2 转子初始结构应力场分布Fig.2 Distribution diagram of initial structure stress field of rotor

取永磁体径向及切向最大应力分别为Fpm_r、Fpm_t，护套径向及切向最大应力分别为Fpj_r、Fpj_t。根据应力场计算结果可以发现永磁体径向应力和护套切向应力最大值出现在转子内侧，Fpm_r为13.78 MPa，Fpj_t为1 048.9 MPa；永磁体切向应力和护套径向应力最大值出现在转子外侧，Fpm_t为22.20 MPa，Fpj_r为3.01 MPa。永磁体和护套的径向应力分布较为均匀，整体呈现由内至外递减分布；永磁体和护套的切向应力分布较不均匀，由于永磁体内表面与隔磁件接触处呈现拉应力，且隔磁件热膨胀系数与永磁体不同，导致局部产生应力集中。

1.2 参数化模型

考虑将护套厚度、永磁体厚度、永磁体和隔磁件与护套间装配过盈量以及工况温度设为优化变量，故将永磁体外表面直径D设为常数172 mm，永磁体与转子铁心间胶层厚度g设为常数0.2 mm，转子铁心直径设为参数D1，护套外表面直径设为参数D2，过盈量设为参数δ，温度参数设为T，表贴式高速永磁电机转子结构参数如图3 所示，结合表贴式高速永磁电机的实际应用情况，设计参数的变化范围见表2。

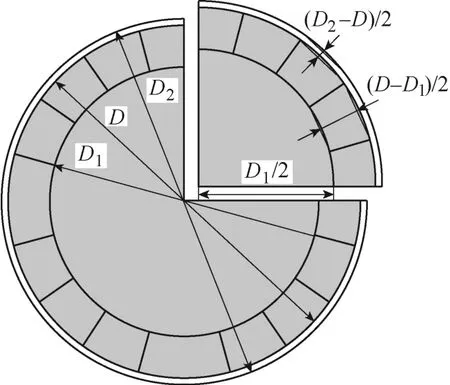
图3 表贴式高速永磁电机转子结构参数Fig.3 Rotor structure parameter diagram of surface attached high speed permanent magnet motor

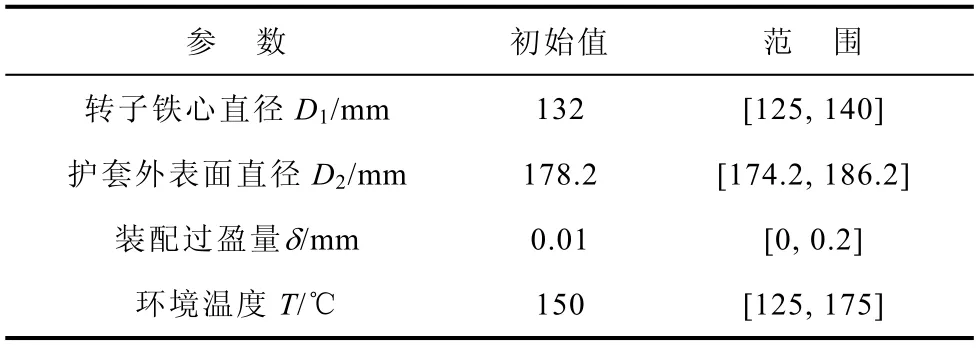
表2 优化参数及范围Tab.2 Optimize parameters and range

2 基于FEM 和EA 算法优化设计

2.1 优化流程

进化算法是模拟自然界生物进化过程的随机搜索方法，应用随机搜索策略，经典进化算法由三部分组成：变异、交叉和选择操作。本文的优化目标即是永磁体径向、切向最大应力及护套径向、切向应力的最大值尽可能小，属于多目标优化问题，适合选用EA 优化算法多次调用参数化的有限元模型进行表贴式高速永磁电机转子强度的优化设计，基于FEM 模型和EA 算法相结合的优化设计流程如图4 所示。

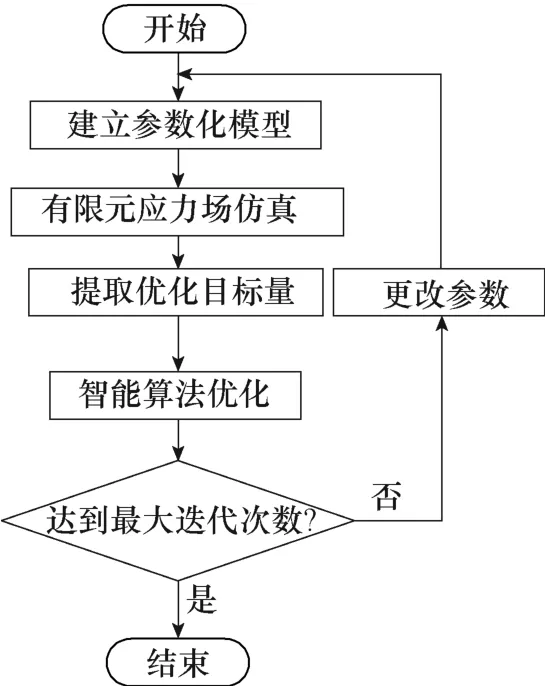
图4 基于FEM 优化设计流程Fig.4 Flow chart of optimization design based on FEM

根据选取的优化参数D1、D2、δ、T，建立关于约束条件及优化目标的数学模型，即

式中，x为优化控制变量；F为多目标优化函数。

2.2 优化结果

利用EA 算法对表贴式高速永磁电机转子强度的优化迭代过程如图5 所示，综合考虑永磁体径向最大应力Fpm_r、切向最大应力Fpm_t及护套径向最大应力Fpj_r、切向最大应力Fpj_t，在迭代第206 次时达到最优设计。

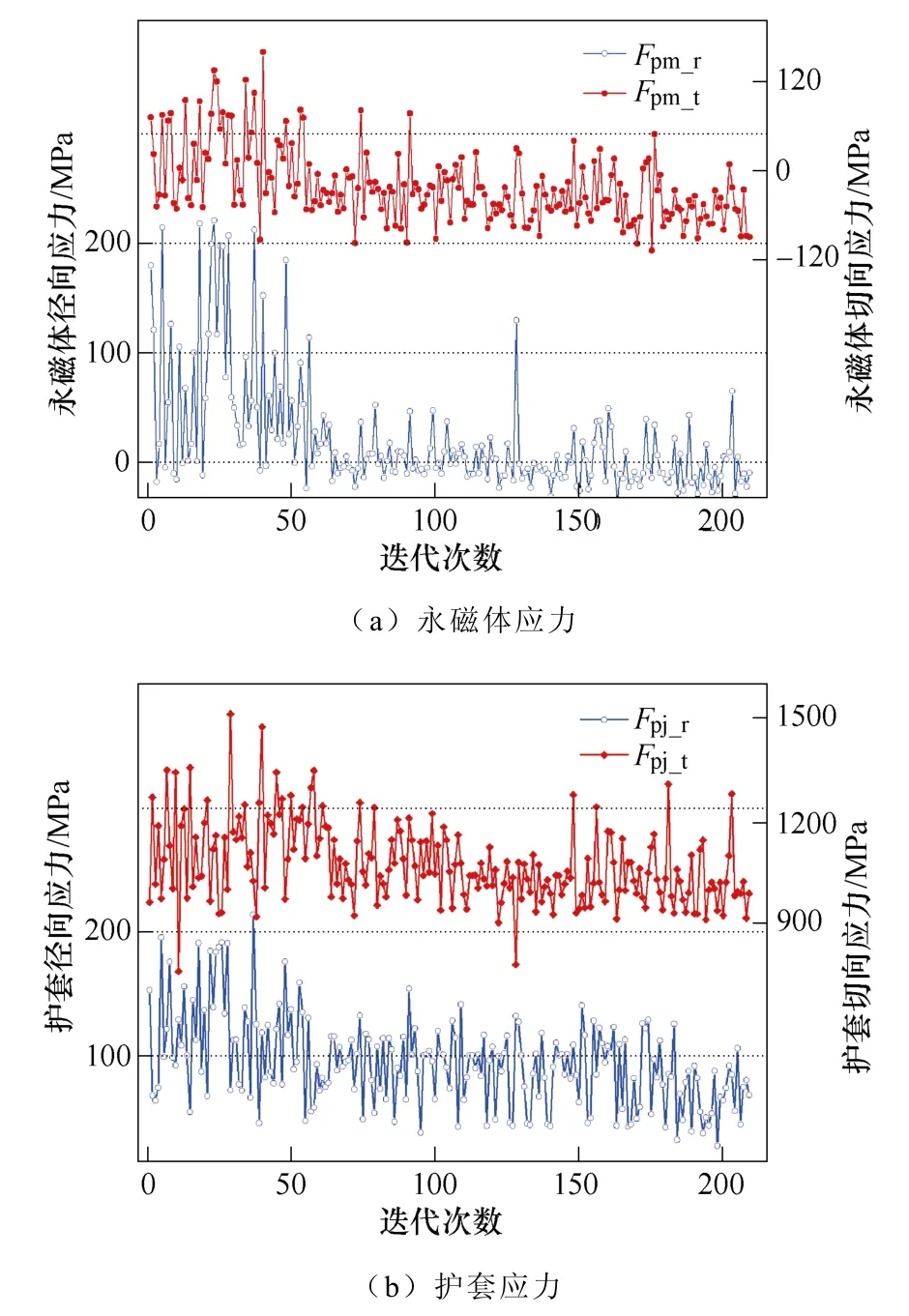
图5 基于FEM 优化迭代过程Fig.5 Iterative process was optimized based on FEM

基于上述优化迭代过程得到的最优设计的应力场分布如图6 所示，优化参数及优化指标见表3。

图6 基于FEM 优化后应力分布Fig.6 Based on FEM optimized stress distribution diagram

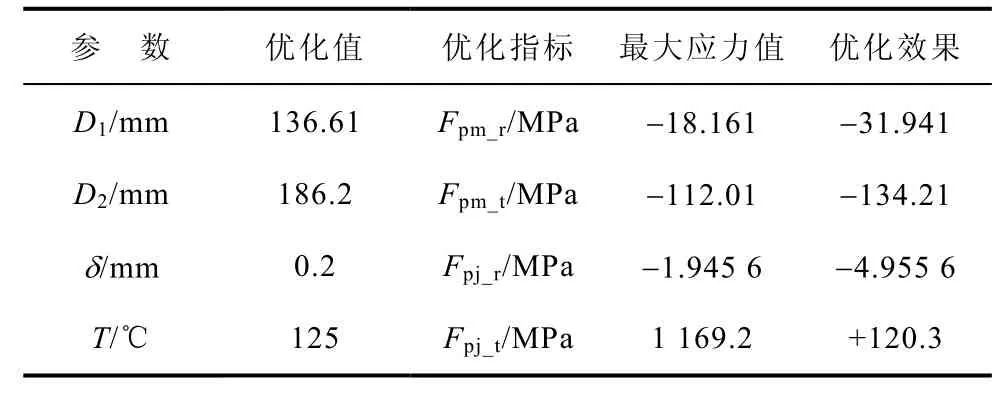
表3 基于FEM 优化设计结果Tab.3 Based on FEM optimization design results

基于FEM 优化后得到的最优设计结果的应力分布可以发现：永磁体径向应力及护套径向应力分布与优化前差别不大，依旧较为均匀，最大值Fpm_r出现在与隔磁件接触面上，最大值Fpj_r出现在护套外表面；永磁体切向应力分布与优化前相比变得均匀且整体呈现由内表面至外表面递减的趋势，最大值Fpm_t出现在与胶层相接的内表面中心；护套切向应力分布与优化前相近，较大应力集中在永磁体与其接触面上，较小应力集中在隔磁件与其接触面上，最大值Fpj_t出现在隔磁件与永磁体接触面对应的护套内表面位置，结果见表3。

根据基于FEM 优化后得到的最优设计结果可以发现：优化后铁心直径D1增大，即永磁体厚度变大，护套外表面直径D2增大至所定范围的上限186.2 mm，即护套厚度达到最大，永磁体和隔磁件与护套间装配过盈量δ增大至所定范围的上限0.2 mm，工况温度减小至锁定范围的下限125 ℃；获得的优化效果包括永磁体径向最大应力Fpm_r及切向最大应力Fpm_t、护套径向最大应力Fpj_r，分别降低了31.941 MPa、134.21 MPa、4.955 6 MPa，其中对永磁体切向最大应力Fpm_t的优化效果最好，护套切向最大应力Fpj_t增大，但也符合工程实际的要求，在强度极限以内。综上所述，说明利用FEM 结合EA 优化算法的优化方法可以取得优化效果，但由于FEM 优化设计收敛困难且愈发耗时，应探索近似代理模型在电机优化领域的可行性。

3 基于Kriging 模型和EA 算法优化设计

3.1 建立Kriging 近似模型

Kriging 近似模型是一种代表性的数学模型，本质是逼近输入变量与输出变量间的关系曲线或响应面[19]，在满足近似精度要求的前提下可替代复杂的FEM 求解器，进行更多次运算的同时耗时更少，提高全局寻优速率。而采用合理的样本点生成方法是建立近似模型的基础，并且近似模型的拟合质量在一定程度上取决于初始样本数据的质量，所以选用拉丁超立方抽样（Latin Hypercube Sampling,LHS）方法生成200 个样本的空间。拉丁超立方抽样是一种分层随机抽样，能够从变量的分布区间进行高效采样，达到以尽量少的样本点充分覆盖设计空间，有效反应输入参数的变化以及输出与输入参数的关系，同时避免聚集和多余相关性。

近似代理模型的拟合质量一般随着输入参数的增加而降低，文中涉及的输入参数较少，且应用稳态仿真分析，所以适合用于近似。基于有限次数的有限元模型求解器计算完成拟合预测得到 Kriging近似模型，具体基于Kriging 模型进行优化的流程如图7 所示。

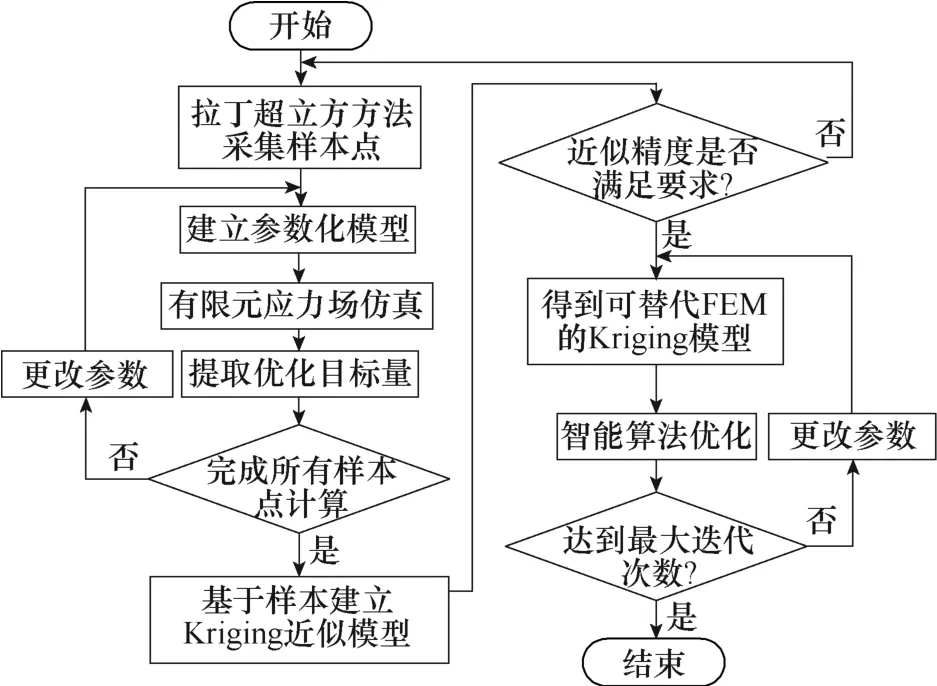
图7 基于Kriging 模型优化流程Fig.7 Optimized flow chart based on Kriging model

基于预测模型智能优化的关键是采用数值拟合方法描述响应参数与输入参数的函数关系，Kriging模型基于每个样本点插值，一般将系统的响应值与设计变量之间的关系形式设为[20]

式中，y(x)为响应函数；f(x)为用作近似基本模型的多项式函数；z(x)为表示有关y(x)均值的不确定性的随机函数。

3.2 Kriging 近似模型拟合精度分析

近似模型拟合精度分析的目的是确保可以有效地表达原始模型中所包含的信息，本文采用预测系数（Coefficient of Prognosis,COP）作为衡量近似模型准确性的判据。预测系数（COP）最初是2008 年Most 和Will 提出的一种评估模型质量的方法，基于交叉验证算法量化评价近似模型的预测质量，是一个客观的评价指标。预测系数COP 值越高，近似模型的拟合精度越高，与实际的模型越接近，COP＞0.7 时，可以认为拟合精度较高。COP 的定义为

表4 优化指标近似精度Tab.4 Optimization index approximate accuracy

3.3 优化结果

基于Kriging 模型结合EA 算法得到的最优设计的优化指标近似值与FEM 计算值对比见表5。根据表5 中得到的偏差可以发现，基于FEM 和近似模型对最优设计进行的最大应力仿真结果相接近，偏差均在合理范围内。优化后的转子应力场分布如图8所示，优化参数及优化指标见表6。

表5 最优设计优化指标近似值与FEM 值对比Tab.5 The approximate value of optimal design optimization index was compared with the FEM value

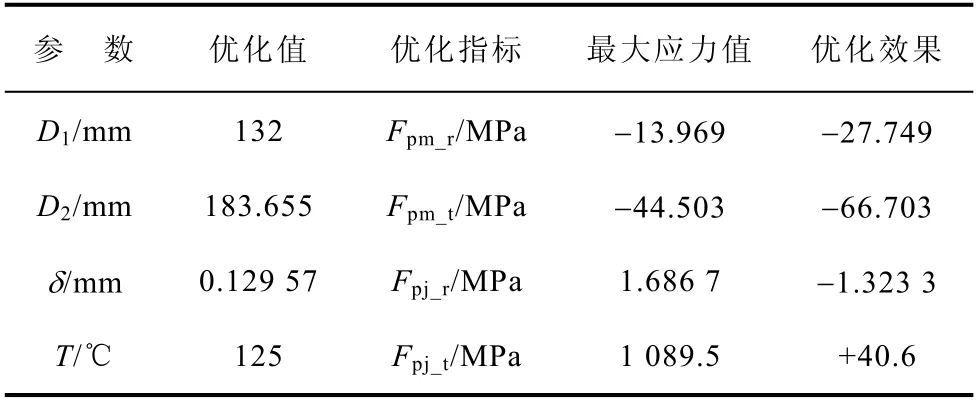
表6 基于近似模型优化参数和优化指标Tab.6 Design results were optimized based on approximate model

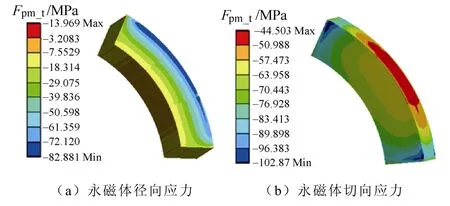
根据基于Kriging 模型优化后得到的最优设计结果的应力分布可以发现：永磁体径向应力及护套径向应力分布较为均匀，分别呈现由内至外应力逐渐减小和逐渐增大的趋势，最大值Fpm_r和Fpj_r出现在永磁体内表面和护套外表面；永磁体切向应力呈中心至两端逐渐减小分布，最大值Fpm_t出现在外表面中心；护套切向应力分布存在两个应力集中处，即最大值Fpj_t出现在隔磁件与其接触面中心处，而较小应力集中在永磁体与其接触面上。根据基于Kriging 模型优化后得到的最优设计结果可以发现：优化后铁心直径D1与初始结构相同，为132 mm，即永磁体厚度保持不变，护套外表面直径D2增大至183.655 mm，即护套厚度增大2.827 5 mm，永磁体和隔磁件与护套间装配过盈量δ增大至0.129 57 mm，工况温度如基于FEM 的优化结果，降低至所定范围的下限，即最低温度125 ℃，优化指标除Fpj_t外均得到降低，Fpm_r、Fpm_t、Fpj_r分别减小27.749 MPa、66.703 MPa、1.323 3 MPa，但降低值均小于基于FEM 优化取得的最优设计，Fpj_t增加后为1 089.5 MPa，也在碳钎维的强度极限范围内。

4 优化结果对比分析

经上述两种技术路线优化后的转子几何结构如图9 所示。基于FEM 优化后的永磁体厚度变薄，由初始的20 mm 变为17.695 mm，护套厚度达到最厚，由初始的 3 mm 变为 7 mm，过盈量δ由初始的0.01 mm 变为0.2 mm，工况温度降低至125 ℃；基于 Kriging 近似模型优化后的永磁体厚度保持20 mm 不变，护套厚度增大，达到5.827 5 mm，过盈量δ由初始的0.01 mm 提升至0.129 57 mm，工况温度变化与基于FEM 优化的变化相同，达到设定范围内最低温度125 ℃。

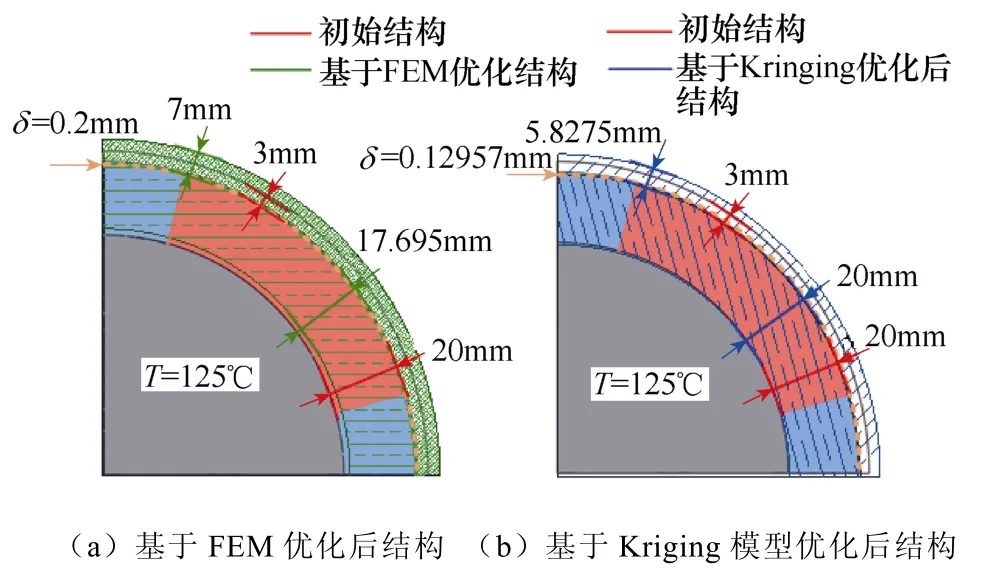
图9 两种技术路线所得最优设计结构Fig.9 The optimal design structure diagram of the two technical routes is obtained

两种优化设计路线的样本点分布如图10 所示，耗时对比见表7。

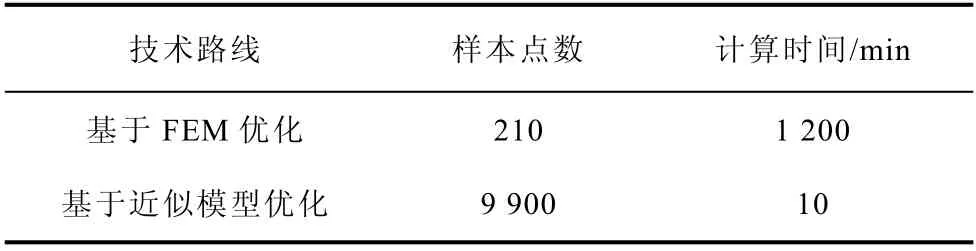
表7 基于FEM 与基于近似模型优化对比Tab.7 FEM based and approximate model based optimization comparison

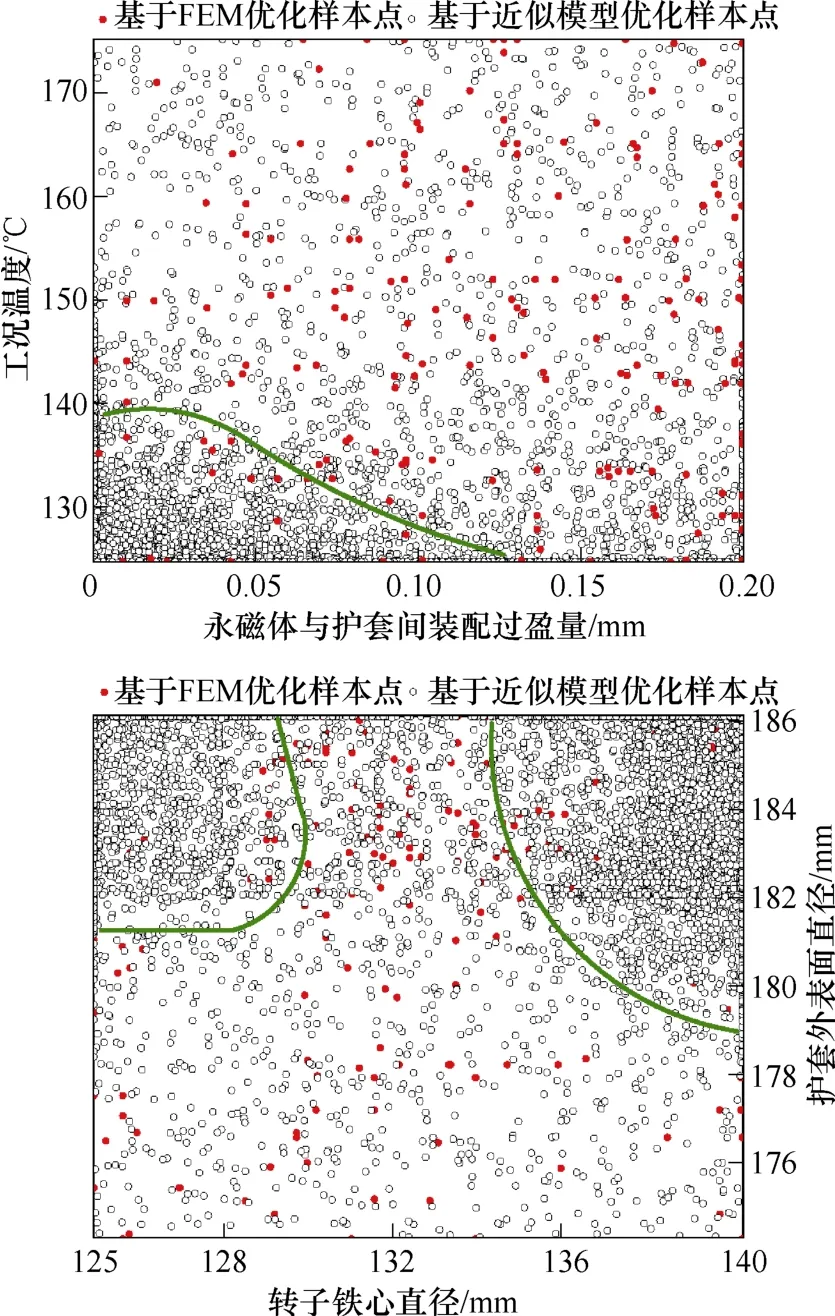
图10 优化设计样本点示意图Fig.10 Optimize design sample point schematic diagram

首先由图10 及表7 可以发现，基于近似模型优化的样本点分布更广泛，达到了近万次的优化，是基于FEM 优化次数的近50 倍，同时耗时是基于FEM 优化的近1/50，说明了基于近似模型优化的快捷性，而基于Kriging 模型优化稍差于基于FEM 优化取得的效果。通过图10 样本点对比可以发现，基于近似模型优化的样本点的聚集性，工况温度T和过盈量δ多集中分布于设定范围的下限，护套外表面直径D2集中在设定范围的上限，转子铁心直径D1集中在设定范围的两端，实则反映了工况温度T尽可能低、过盈量δ尽可能小、护套尽可能厚时有利于转子强度的提升。所以基于近似代理模型的优化方法更侧重于优化参数规律的找寻，判断样本点的集中分布情况，从而可以得出优化指标与优化参数间的基本关系，适用于初始寻优阶段。

5 结论

本文以1.12 MW、18 000 r/min 的表贴式高速永磁电机转子为优化对象，建立其参数化几何模型，应用有限元法分析了电机转子的应力场分布。分别采用基于FEM 和Kriging 近似模型结合EA 优化算法对表贴式永磁电机的转子强度进行了优化设计，并对两种优化方法进行了对比分析得到如下结论：

通过建立电机转子的参数化有限元模型，以不同结构参数及温度参数下的永磁体及护套径向、切向最大应力作为EA 算法中的优化目标量，经过多次迭代优化后，能够得出使得永磁体径向及切向应力最大值、护套径向应力最大值均减小的护套厚度、永磁体厚度、温度和过盈量的最优解。说明基于FEM 结合EA 算法的优化方法具有一定优化效果，但也存在优化尝试少且优化时间长的问题。

基于FEM 和Kriging 近似模型结合EA 优化算法的两种技术路线所得最优设计的优化参数：护套厚度、永磁体厚度、温度以及优化目标量：护套、永磁体应力最大值等计算结果接近，说明EA 算法可以比较准确地得出使转子强度取得提升的结构参数。相对基于FEM 的优化方法，基于Kriging 近似模型的优化方法不受限于样本数量，计算时间更短，计算效率更高，优化参数过多时可能存在拟合精度低导致优化设计准确性差等问题，但是基于样本空间中样本点的分布情况可以直观地反映优化参数与优化目标量间的关系，适用于初始寻优阶段，在实际工程优化问题中也具有一定的研究意义。

实际工程中的优化问题应结合两种优化技术路线，初步寻优阶段采用基于近似模型优化方法精确优化参数范围，进而采用基于FEM 优化方法展开优化并取得最优设计结果。