隧道爆破对临近特高压铁塔影响研究

王 炎，沈晓莉，陈金苗，曹成杰

(1.浙江理工大学建筑工程学院，浙江 杭州 310018；2.中国电建集团华东勘测设计研究院有限公司，浙江 杭州 310000；3.浙江存真土木工程技术有限公司，浙江 杭州 310018)

随着我国经济的快速发展，城际交通网日益发达，高速铁路建设快速发展，施工过程中通常伴随着山区复杂环境下的隧道工程。在隧道爆破掘进过程中，隧道往往会临近或下穿一些重要的地表敏感性建筑物，并在一定程度上引起地表建筑物的振动，当建筑物振速达到临界值，会形成不同程度的损坏[1- 5]。针对隧道爆破对周边建筑物的影响问题，许多学者进行了相关的研究。如王佳辉等[6]结合某隧道爆破工程，采用Midas/GTS建立有限元模型，对引水渠振速进行现场监测，并将结果与数值模拟结果进行对比，结果表明：引水渠竖直方向振动速度最大，水平垂向最小。武泽等[7]结合某隧道爆破工程，利用LS-DYNA建立有限元模型，研究爆破施工对周围埋地管道的影响，结果表明：相比于国外类似工程的经验数值，埋地管道的振动速度较低，且数值模拟得到的管道各项动态响应小于管道强度。樊浩博等[8]结合某隧道工程，采用数值模拟的方法对临近建筑物的振动进行了监测，结果表明：建筑物的竖直方向振动速度远大于水平方向，且随着时间和爆心距的增大，振动速度迅速衰减。茶增云等[9]结合某隧道工程，通过将现场实测数据与数值模拟结果相结合，研究连拱隧道中后行洞爆破施工过程中对先行洞的影响。结果表明：建立的离散元模型可以反映工程实际，且后行洞施工会对先行洞产生一定影响，需在施工中控制炸药量。

上述研究均是针对低层建筑结构进行研究，对于例如高压铁塔这种的高耸建筑研究较少。当隧道临近高压输电铁塔时，爆破会使地表的高压铁塔塔基产生振动，甚至导致铁塔结构失稳，所以研究隧道爆破对临近高压铁塔的影响有重大意义。肖欣欣等[10]结合某隧道工程，采用FLAC3D进行数值模拟，重点研究分析了铁塔塔基的沉降及振动速度；伍岳等[11]结合某高速公路隧道工程，对公路旁临近的高压铁塔塔基振动进行了现场监测，重点研究了高压铁塔的振动响应特征。上述研究对避免爆破诱发地表铁塔塔基震动失稳有重大贡献，但是目前国内外针对多座、近距离、特高压铁塔爆破控制的研究较少，本文结合杭温铁路郎家畈隧道工程项目，根据萨道夫斯基公式，以铁塔与爆源直线距离最近、单响炸药量最大为最不利工况，采用Midas/GTS有限元软件建立二维模型，并结合现场监测振速，研究隧道爆破对临近两座特高压铁塔和一座高压铁塔的影响，为今后类似研究提供一些理论依据。

1 工程概况

新建杭温铁路郎家畈隧道段位于金华市浦江县檀溪镇上河村，正线施工里程DK91+675.19～DK92+143.27，全长467.18m，隧道围岩Ⅲ、Ⅳ、Ⅴ级分布。进出口洞门分别长19.81、18m，隧道进口靠近壶源江大桥，出口连接上河中桥。从进口掘进施工，明洞段采用明挖法施工，暗挖段采用钻爆法开挖。各作业面分别配备大型机械作业。开挖采用钻爆法掘进，Ⅲ级围岩采用台阶法施工，Ⅳ级围岩采用三台阶法施工，Ⅴ级围岩采用三台阶临时仰拱法施工。

隧道线路东南侧有1000kV电力铁塔2座，500kV电力铁塔1座，1#—2#电力铁塔属于浙北-福州特高压交流输变电线路，塔型为酒杯塔，塔高91.6m。3#电力铁塔塔型为干字塔，塔高66m(为表示方便本文沿隧道施工方向将3座电力铁塔记为1#—3#)，隧道和铁塔具体相对位置关系如图1所示。1#铁塔与隧道顶垂直净距约为38.92m，开挖边线距塔基最小水平距离约为32.47m，与隧道的最小直线距离约为58.79m；2#铁塔与隧道顶垂直净距约为84.78m，开挖边线距塔基最小水平距离约为62.55m，与隧道的最小直线距离约为105.36m；3#铁塔与隧道顶垂直净距约为41.16m，开挖边线距塔基最小水平距离约为18.94m，与隧道的最小直线距离约为45.31m。隧道与铁塔相对位置关系剖面图如图2所示。

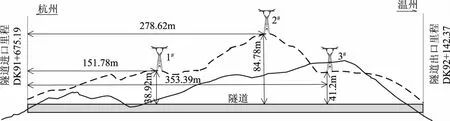
图1 隧道与铁塔位置示意图

图2 电力铁塔与隧道相对位置剖面图

2 爆破振动监测

2.1 监测方案

实际工程中在3座铁塔塔基上分别布置1个振动监测点，安装三轴振动传感器。监测使用的是L20-N数据采集设备及配套软件，采集精度高，可满足本工程监测需求。为了保证采集到的振动信号的有效性和振动波形的完整性，设置的触发电平为0.5mm/s，采样频率2000Hz，监测周期2s。监测点布置如图3所示，R为铁塔塔基测点和隧道爆心的直线距离，即爆心距。

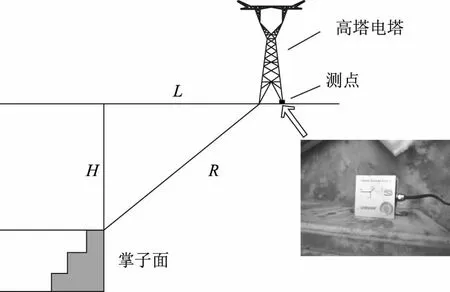
图3 监测点布置图

2.2 监测结果分析

由于1#铁塔剖面围岩等级为Ⅴ级，在施工设计中，下台阶爆破单响药量设计值最大，故考虑1#铁塔正下方、下台阶爆破时为最不利工况。2#铁塔和3#铁塔剖面围岩等级为Ⅲ级，在施工设计中，上台阶爆破单响药量设计值最大，故考虑2#铁塔和3#铁塔正下方、上台阶爆破时为最不利工况。因此提取1#铁塔下台、2#铁塔和3#铁塔上台爆破时，3座铁塔水平爆心距为50、40、30、20、10、0m处塔基的监测数据，结果见表1。

表1 铁塔最大振速结果统计表

由表1可看出在爆心距为50m时，1#铁塔塔基振动速度为0.0625cm/s，在爆心距为0m时，1#铁塔塔基振动速度最为0.1929cm/s；2#铁塔塔基振动速度为0.1381cm/s，在爆心距为0m时，2#铁塔塔基振动速度最为0.4721cm/s；3#铁塔塔基振动速度为0.4033cm/s，在爆心距为0m时，3#铁塔塔基振动速度最为1.2657cm/s；3座铁塔的塔基振速均远小于GB 6722—2014《爆破安全规程》规定的安全允许振速2.5cm/s，可知爆破振动对高压铁塔的影响较小，3座铁塔处于安全状态证明爆破方案合理可行。

爆破振动速度隧爆心距的变化规律如图4所示。由图可知随着爆心距的增大，各塔塔基最大振动速度均呈减小趋势，说明各塔塔基振动速度随水平爆心距的减小而增大。水平爆心距越近，振动速度衰减越快，水平爆心距越远，振动速度衰减越慢。相比1#铁塔、2#铁塔，3#塔最大振速随爆心距变化趋势较为明显;同时，在相同炸药量的情况下，距离隧道爆破掌子面直线距离更近的3#铁塔塔基振速明显大于2#铁塔塔基，表明在现场应重点关注3#电力铁塔的结构安全。

图4 监测点布置图

3 数值模型及荷载

3.1 数值模型与参数

为进一步分析郎家畈隧道爆破振动对高压铁塔的影响，采用Midas/GTS对隧道爆破开挖进行二维模拟。计算剖面选取各电力铁塔与郎家畈隧道对应横断面，模型尺寸根据隧道及输电铁塔的断面尺寸确定，边界超出计算构筑物或隧道的距离不小于30m。在保证计算精度的情况下，采用混合网格法划分模型，对隧道周围进行尺寸控制，网格进行加密处理。二维有限元模型如图5所示。

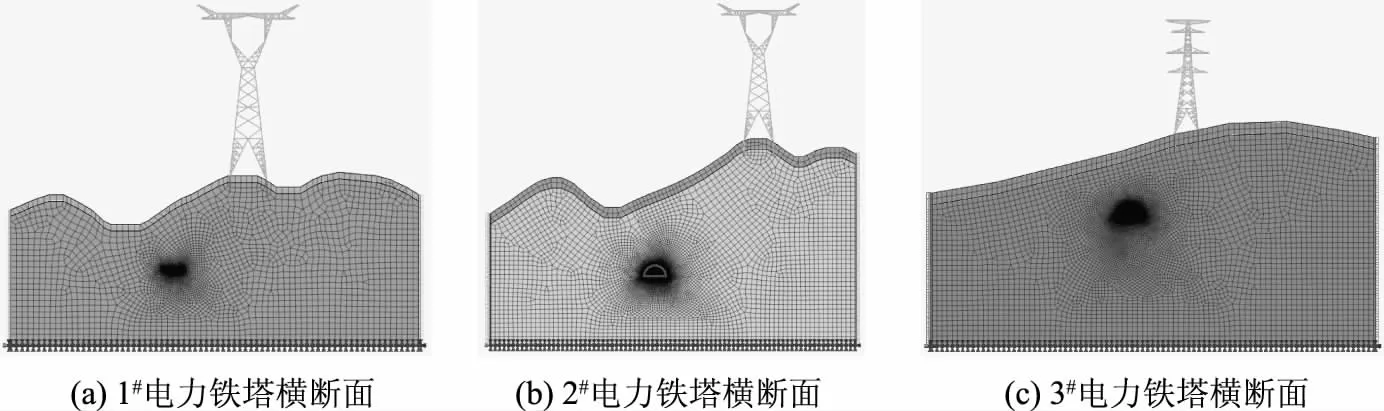
图5 二维有限元模型图

1#铁塔横断面隧道周围围岩主要以Ⅴ级围岩为主，2#铁塔和3#铁塔横断面隧道周围围岩主要以Ⅲ级围岩为主，因此二维模型岩土采取Ⅲ、Ⅴ级围岩，围岩采用基于莫尔-库仑屈服准则的弹塑性本构模型模拟。铁塔为Q235钢材，模型采用桁架单元进行模拟，桩基为C25混凝土，模型采用梁单元进行模拟。模型具体参数取值见表2。

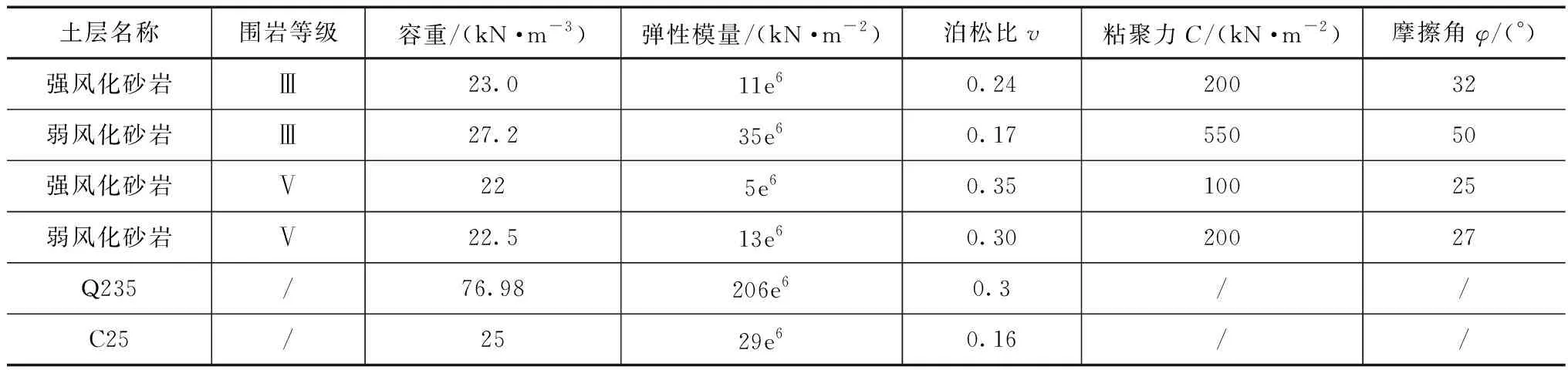
表2 有限元模型参数表

3.2 边界约束

对于动力分析，建立一般的边界条件会由于波的反射作用而产生很大的误差；因此时程分析时采用黏性边界条件。模型底部的约束条件为水平、竖直方向都固定；模型两侧约束条件对于爆破动力计算采用1972年Lysmer和Wass提议的粘性边界(viscous Boundary)。为了定义粘性边界需要计算相应的土体x，y，z方向的阻尼比。计算阻尼的公式如下。

(1)

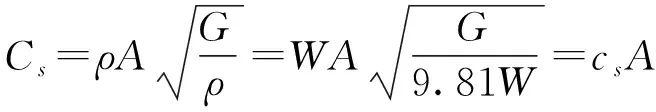
(2)

式中，λ—体积弹性系数，kN/m2；G—剪切弹性系数，kN/m2；E—弹性模量；v—泊松比；A—截面积，m2。

3.3 爆破荷载

二维计算采用张玉成[12]提出的爆破数值模拟方法，即在炮孔壁之上直接施加半理论半经验的指数衰减型荷载爆破荷载压力曲线，结合爆轰理论和爆腔膨胀理论，依据工程经验和试爆破时实测结果来确定衰减函数的部分参数。基于圣维南原理[12- 15]，在建模时不考虑等效荷载炮孔形状，爆破荷载时程曲线以压力的形式施加在炮孔或者隧道周边，荷载作用方向为炮孔或者隧道周边的垂直方向。此时的荷载峰值用International Society of Explosive Engineers(2000)里提及的公式。计算中各参数取值见表3。

PD=2.5×10-6×S×V

(3)

(4)

式中，PD—爆破压力，kbar；PB=孔壁面上的压，kbar；V—爆破速度，m/sec；dc—火药直径，mm；dh—孔眼直径，mm；S—炸药密度，g/cm3。

表3 不同围岩的爆破冲击荷载

根据是否考虑爆破孔周长的影响，最大爆破压力可按P′=PB×W计算，W为最大装药量，单位为kg。上式决定了爆破时发生的空气动力压力的大小，及实际上作用在孔壁的动压力随时间的变化状态。时程动压力PD可按照Statfiled和Pugliese(1968)经验公式计算，具体如下:

(5)

式中，B=1000—荷载常数，控制荷载随时间衰减的快慢程度。

与现场实际一致，1#铁塔二维模型取下台阶进行验算分析，下台阶底板孔总计14个，单孔最大装药量为0.7kg，最大等效爆破荷载为0.88MPa，数值模型中荷载作用于下部台阶底板孔孔壁上。2#铁塔和3#铁塔二维模型取上台阶进行验算分析。上台阶周边孔总计40个，单孔最大装药量为0.70kg，最大等效爆破荷载为2.20MPa，数值模型中作用于上部台阶周边孔孔壁上。最终得到如图6—7所示的爆破时程荷载函数曲线。

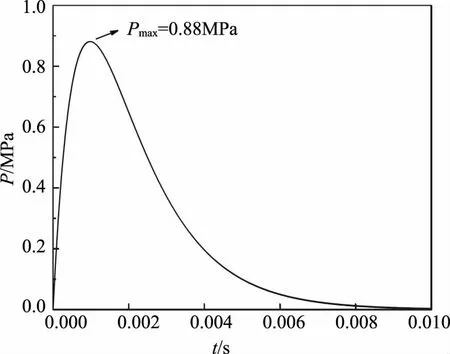
图6 1#铁塔剖面脉冲荷载时程曲线

图7 2#和3#铁塔剖面脉冲荷载时程曲线

3.4 计算结果分析

在最不利工况下，分别提取3座铁塔的振速、位移、应力，分析隧道爆破对电力铁塔的影响。

3.4.1铁塔振速分析

在数值模型中，分别对1#铁塔下台、2#铁塔和3#铁塔施加上台施加爆破荷载，通过有限元时程分析，得出3座铁塔的振速，结果如图8所示，见表4。分析结果可知，1#铁塔塔基最大振速为0.13cm/s；2#铁塔塔基最大振速为0.41cm/s；3#铁塔塔基最大振速为1.12cm/s；3座铁塔振速均小于GB 6722—2014规定的安全允许振速2.5cm/s；其中，3#铁塔振速最大，在实际爆破过程中，要着重保护与监测3#铁塔的结构安全。

图8 铁塔振速结果云图

表4 铁塔振速结果统计表

将模拟后的最大振速与现场实测数据进行对比，结果如图9所示。分析可知，数值模拟结果与现场监测结果较为接近；在相同炸药量的情况下，爆心距更小的3#铁塔振速明显大于2#铁塔，这与萨道夫斯基公式相符。故二维数值模型可靠，具有较高的模拟精度，可用于隧道爆破振动影响分析。

图9 实测与模拟振速对比

3.4.2铁塔位移分析

通过有限元时程分析，得出3座铁塔在最不利工况下的位移和倾斜率，结果如图10所示，见表5。分析可知，①1#铁塔塔基竖直方向上最大位移为-0.0015mm，塔基倾斜率为9.1×10-9；2#铁塔塔基竖直方向上最大位移为0.0077mm，塔基倾斜率为4.9×10-7；3#铁塔塔基竖直方向上最大位移为0.0035mm，塔基倾斜率为6×10-8；根据DLT 5219—2014《架空输电线路基础设计技术规程》，3座铁塔的塔基倾斜率均远小于不均匀沉降的允许值0.005，可知铁塔在隧道爆破过程中处于安全状态。②3座铁塔中，2#铁塔倾斜率最大。数值模型中，2#铁塔和3#铁塔所用炸药量相同，但爆心距更小的3#铁塔倾斜率小于2#铁塔，说明铁塔高度对铁塔塔基的倾斜率影响较大，在实际施工过程中应关注2#铁塔的倾斜位移情况。

图10 铁塔位移结果云图

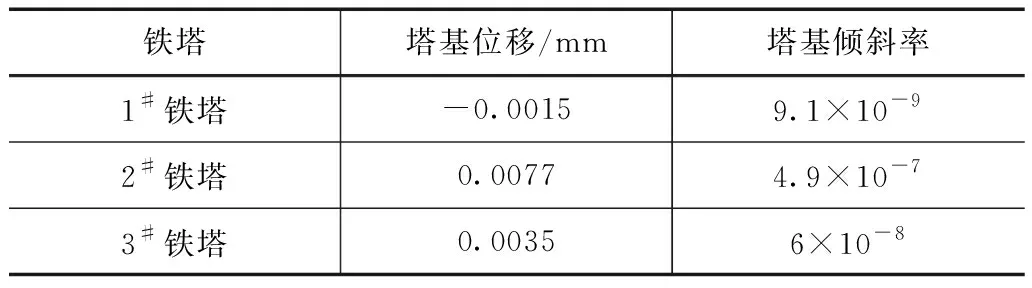
表5 铁塔位移结果统计表

3.4.3铁塔应力分析

通过有限元时程分析，得出3座铁塔的在爆破荷载作用下产生的最大应力，结果如图11所示，见表6。分析可知，1#铁塔塔基最大拉应力大小为0.07MPa，最大压应力大小为0.07MPa；2#铁塔塔基最大拉应力大小为0.23MPa，最大压应力大小为0.20MPa；3#铁塔塔基最大拉应力大小为0.57MPa，最大压应力大小为0.59MPa；3座铁塔最大应力均出现在塔基处，且均小于钢材的许用应力，因此可知实际爆破施工过程中控制炸药量合理，能够保证铁塔的结构安全。

表6 铁塔最大应力结果统计表

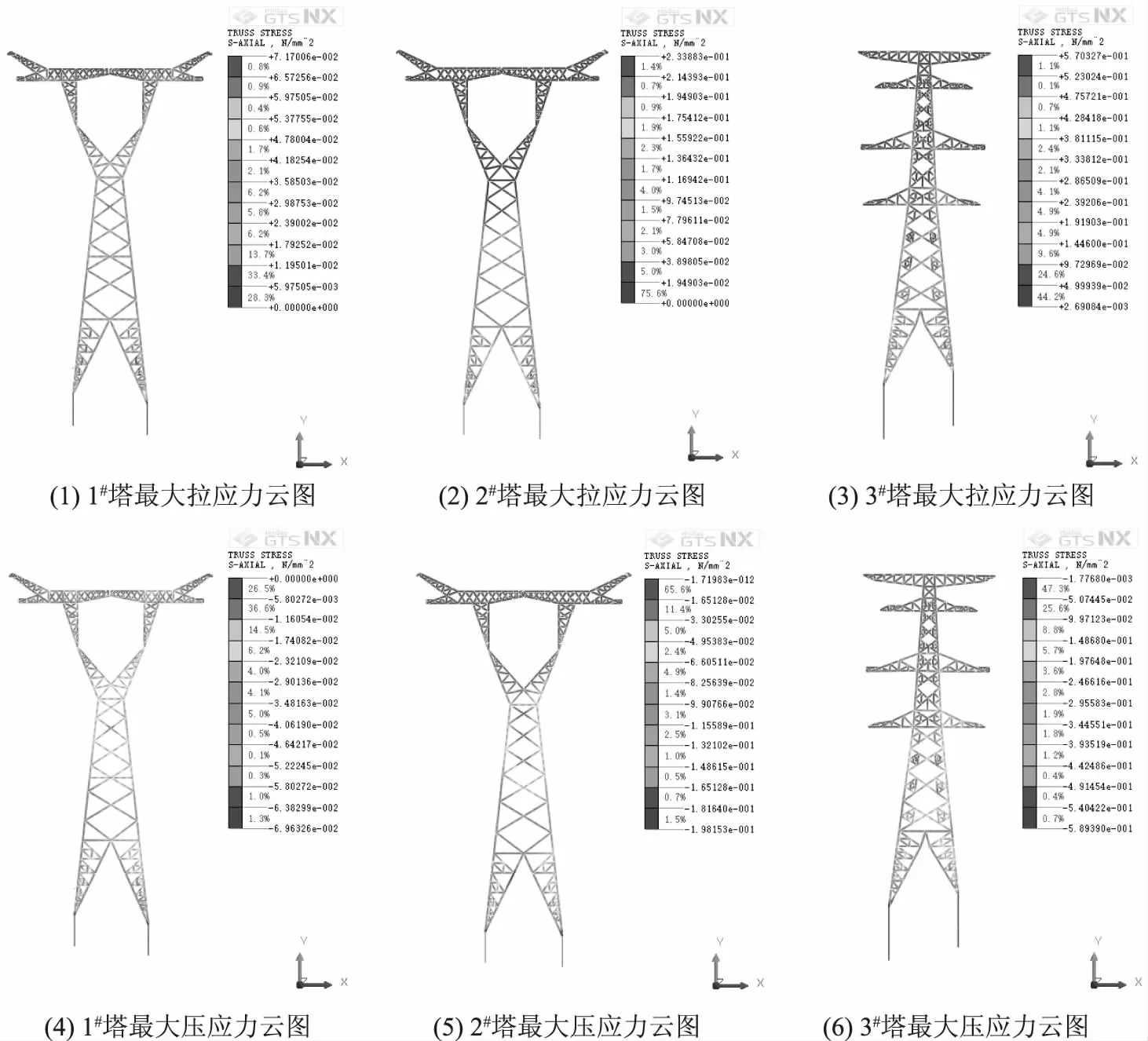
图11 铁塔振速结果云图

4 结语

通过现场实测和数值分析，研究在铁塔和爆源直线距离最近、单响最大炸药量的最不利工况下隧道爆破对临近3座特高压电力铁塔的影响，得到如下结论：

(1)现场监测结果表明，3座塔塔基振动速度均随水平爆心距的减小而增大，3座铁塔振速均未超过GB 6722—2014规定的安全允许振速2.5cm/s，铁塔处于安全状态。其中，3#塔最大振速随爆心距变化趋势较为明显；且在相同炸药量的情况下，爆心距更小的3#铁塔振速明显大于2#铁塔，说明在实际爆破过程中，要着重保护与监测3#铁塔的结构安全。

(2)数值模拟结果表明，3座铁塔塔基的最大倾斜率均小于0.005，满足DLT 5219—2014规范要求，3座铁塔处于安全范围。其中，爆心距相对较大2#铁塔塔基倾斜率最大，说明塔高对铁塔塔基倾斜率影响较大，在实际施工过程中应着重关注2#铁塔的倾斜位移情况。

(3)数值模拟结果表明，3座铁塔的最大应力均为未超过钢材的许用应力，表明实际爆破施工中控制炸药量合理，可保证铁塔的结构安全。

(4)数值模拟结果与现场监测结果误差较小，可知本文建立的有限元模型合理，说明采用数值软件模拟隧道爆破对临近特高压铁塔的影响是可行的。