基于有限元的电力电缆缆芯温度预测方法

谭静，吴叶弘，田鹏

（1.国网湖北省电力有限公司直流公司，宜昌 443000； 2. 上海乐研电气有限公司，上海 201802）

引言

电力作为人们生产、生活不可缺少的一部分，电力安全受到社会各界的广泛关注与重视。电力传输过程中主要设备是电缆，其可靠性对电网运行效果产生重要的影响。调查电力系统发生火灾的原因发现，大多是因电力电缆长时期处于高压供电状态下导致电缆发热引起的火灾[1]。如果电缆局部温度上升，会在一定程度上破坏自身的绝缘介质，进而影响电力系统安全的运行。而已有电缆检测系统旨在实时采集电缆表面的温度，并未对缆芯温度实施预测。电缆缆芯温度可以更好地反映出电缆运行情况，做好缆芯温度的预测工作，能够提前预判电缆运行状况，从而保障输电线路安全、可靠的运行。如今，电缆缆芯温度监测系统主要借助在电缆内部设置的光纤传感器对缆芯温度进行测量，这种方法比较直观，但会对电缆内部结构产生破坏，所用成本比较高。蒲路,段玮等学者研究指出，采用有限元软件创建电缆中间接头模型，进而分析环境温度及负荷电流对于电缆接头线及表皮温度带来的影响，能够为电缆中间接头温度监测及状态评估提供一定的依据[2]。文中提出基于有限元对电缆缆芯温度进行预测，结合环境参数、时间序列等指标建立相应的预测模型，进一步检验该模型的有效性。

1 有限元及BP神经网络概述

1.1 有限元分析

如今，通常使用有限差分法、有限元分析法及边界元法对电力电缆温度场进行计算，其中，有限差分法旨在将求解阈分成差分网络，通过大量网络把计算区域取代的方法。通过这种方法能够求出各敷设模式下电缆的温度值，但其不适合用于不规则复杂区域下，难以确保数值解的守恒性。边界元法根据计算域边界采用积分方程替代微分方程，这种方式只需进行少量的计算，花费时间短。但边界元法难以解决比较复杂的边界问题，实际应用中受到一定的限制。有限元分析法依据变分原理任意进行网格划分，满足复杂边界的计算要求。利用有限元分析法对不同物理场耦合进行计算，完成敷设电缆的模拟工作，也是求解电缆温度场分布最佳的方法[3]。有限元分析法的优势在于能够对敷设电缆情况进行精准模拟，从而满足比较复杂、无规则区域的要求，具有较强的适应性[3]。依据电缆结构参数、模型边界等对电缆建立相应的有限元模型，借助环境及负荷参数计算电缆温度场获得缆芯温度，求解过程见图1。

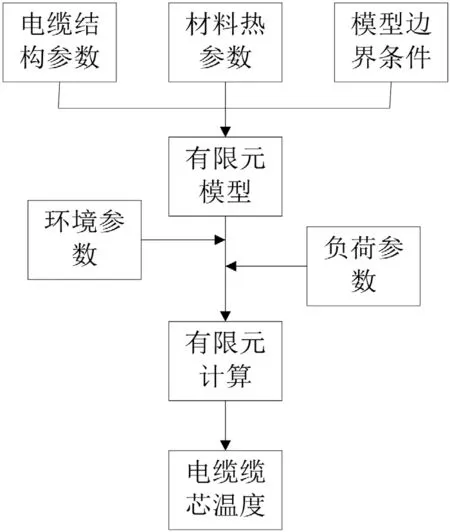
图1 缆芯温度计算过程

在未考虑外热源的前提下，电缆自身引起的线芯损耗、绝缘介质损耗等均会转化成热量，导致电缆本体的温度上升。因热传递的问题，电缆与周边媒介的温度均有所上升。根据IEC-60287标准[5]对内热源进行计算，电缆线芯损耗如下：

式中：

YS、YP—集肤、临近效应系数；

R0—处于20oC条件下导体单位长度的直流电阻；

αc—导体电阻的温度系数；

R′—导体单位长度的直流电阻。

必须注意，受到交变电压的影响，绝缘介质产生的损耗也不能忽视。绝缘介质损耗计算公式如下：

式中：

Di—电缆绝缘层的直径；

ε、tanδ—绝缘介质的节点常数、损耗系数；

c—单位长度电缆的电容值；

dc—电缆线芯的外径。

金属护套损耗主要由环流及涡流损耗组成，其损耗情况与护套接地方法存在密切的关联[6]。金属护套一端与地面相连或交叉互联接地，这种情况下，环流损耗能够忽略不计。如果电缆金属套处于双端接地的情况，涡流损耗则能忽略不计。当金属护套处于两端接地的状态下，求解其环流损耗为：

式中：

RS—电缆护套或者屏蔽层处于最高温度条件下产生的交流电阻，其单位为Ω/m；

X—相邻两根单芯电缆在单位长度下金属护套的电抗值；

Xm—外侧某一条电缆金属护套与另外的单芯电缆线芯导体产生互感。

进行有限元计算过程中，负荷参数会通过体积生成热的形式加载到有限元模型内，依据电缆各热源损耗情况求出体积生成热。求解公式如下：

式中：

i={1，2,3}—表电缆导体、绝缘体以及金属屏蔽层；

ρi、ri—电缆各层电阻率、有效半径；

l—导体长度；

Si—各层面积；

I—流经电缆线芯相应的有效电阻；

Qi—不同层损耗所对应的体积生成热；

Wi—电缆不同层单位长度的损耗。

1.2 BP神经网络

BP网络作为一种使用最广泛的神经网络模型，其能学习、存储大量的输入-输出模式映射关系，无需事前对这种关系进行描述，如图2所示。人工神经网络是开展人工智能研究中常用的一种方法，其非线性映射能力较强。人工神经网络是多层感知器结构，包含输入、输出及多个隐层。BP算法又称作反向误差传递法，主要包含向前、向后传播阶段，其中，在向前阶段，信息自输入层通过逐级变换传输至输入层[7]。这一过程当网络完成训练后执行，计算公式如下：

图2 BP网络示意图

式中：

Op—网络输出值；

F1、F2、…、Fn—不同层的权值函数；

Xp—第p个输入的样本；

W（1）、W(2)、…、W（n）—第1、2…、n层相应的权值向量。

后向阶段就是依据绩效化误差对权矩阵进行调整，这两个阶段的操作均要受到精度的控制，此处，取网络关于第p个样本误差值。

式中：

m—输出层相应神经元的数量；

ypj—第p样本理想状态下输出向量包含第j个元素。

网络对于整个样本集误差测定如下：

实际工作中，输入信息先由输入层节点传送至隐层节点，通过对节点激活函数进行计算后，及时输出不同计算节点的信息，最终获得相应的输出结果。电缆缆芯温度计算中，先依据已有数据，电缆加载流量、表皮温度等信息初始化网络结构及其权值，根据输入的样本求解BP网络每一层神经元输入及输出信号，依据期望输出计算对权值予以修正处理[8]。

2 有限元分析下缆芯温度预测分析

近些年，随着我国国民经济的发展，工业用电量处于不断上升的状态。与此同时，人们的生活质量及水平也有明显的改变，各种家用电器逐渐进入普通家庭，使得社会对于电量的需求明显增加。基于此，安全、稳定运行的电力系统成为确保人民日常生活及工业发展的关键，这种情况下，对于电力系统输电设备、设备检修等提出更高的要求。电力电缆作为比较常用的输电设备，依托收集、汇总电力系统所监测的温度值，用于评估相关设备是否存在故障。对电缆温度进行测量时，采用监测电缆表面温度的方法，虽然能够直观展现部分电缆运行情况，但缆芯温度难以进行测量，而缆芯温度才是评估电缆运行情况的关键。相关数据表明电缆事故频繁发生，引起事故的主要因素在于电缆本体，因电缆自身结构比较复杂，要采用多种材料复合方可制作成为绝缘材料[9,10]。在对电缆故障进行监测时，关注的重点在于电缆主体部分，人工检查旨在对其外部是否出现异常进行检查。而对电缆缆芯温度进行实时监测，能确保电缆不会处于超负荷运行状态下，保证电力系统的运行安全。但实时监测缆芯温度作为世界性的难题，为有效解决因电缆缆芯不断发热升温，导致电缆绝缘体老化失效，提出依托有限元对电缆缆芯温度进行预测的方法，这种方法能够准确预测出电缆缆芯温度，确保电力电网安全、可靠的运行。电缆缆芯温度预测实现流程见图3。电缆缆芯温度预测步骤：

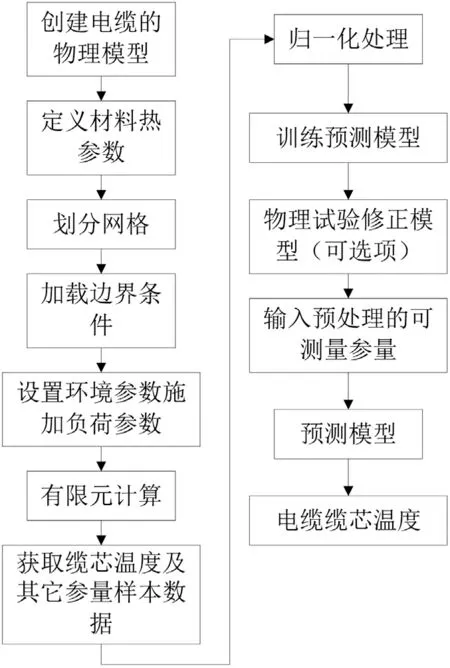
图3 预测算法实现流程

1）根据电缆结构参数、敷设条件等指标信息建立相应的有限元模型；

2）增设环境温度、载荷开展有限元计算，获得电缆相应的温度场分布图。以电缆缆芯相对应节点，查询相关的温度数据，得到所需的样本数据。

3）对缆芯温度及其它能够检测的原始样本数据实施归一化处理。

以X={X1(1)，…X1(n) ，…Xk(1)，…，Xk(n) }、Y={y(n)，y(n+1)，…，y (n+m) }分别当做预测模型的输入、输出变量。

式中：

k—可测量参量的种类数量，例如：环境温度等；

m—预测未来m状态下缆芯的温度；

n—可测量参数相应的时间序列。

4）明确相应的输入变量后，采用BP神经网络对数据实施训练，创建电缆缆芯的温度预测模型。根据实验要求对该模型实施修正，有利于提升所用模型的预测精度。对可测参量进行归一化处理后输入至预测模型内，获得电缆缆芯的温度预测数值。

3 实验结果分析

3.1 建模及样本数据

因受到安装环境、内部结构的影响，使得电力电缆缆芯温度难以直接进行测量。本次研究采用有限元分析获得相应的缆芯温度样本，操作步骤为：温度场建模：挑选二维4节点实体PLANNE55创建相应的二维热传递温度场模型，电缆结构及敷设参数见表1。

表1 电缆结构及敷设参数

模型实施网格划分，文中使用三角形智能划分法。加载温度场模型其边界条件如下：深层土壤温度并未受到电缆的影响，满足第1类边界条件要求，取值如下：tw=25 ℃；由于左侧、右侧土壤与电缆之间的距离较远，达到第2类边界条件，可看成绝热边界进行处理，取值：qw=0；地表土壤与空气之间的接触面，满足第3类边界条件要求，对流换热系数、流体温度恒定值分别为h=8 W/（m2·K）、tf=25 ℃。通过上述操作，得到电缆缆芯温度样本数据，求出并加载相应的运行条件，电缆体积生成热。挑选各单元开展求解计算，获得相应的结果并绘制温度场分布图，获得单回路平面排列及地下直埋敷设方法下，模型温度场见图4。下图中，红色、深蓝色分别代表温度最高、最低的地区。由此可知，模型区的温度以电缆作为中心慢慢向外降低，中间温度最高，达到80.457 ℃。而深层土壤最低的温度值为25 ℃，说明电缆模型温度并未对深层土壤产生较大的影响。基于此，根据电缆缆芯相对应节点，查出这一节点的温度数据，得到电缆缆芯的温度信息。

图4 大型交变盐雾试验室监控软件界面

图4 温度场分布示意图

3.2 预测模型与结果

文中使用BP神经网络创建缆芯温度预测模型，设定其隐层激励函数是tansigmoid、输出层是Linear函数。下文选取某地区发电厂夏季的报表信息，自2021年8月1日至31日的数据，对电缆开展有限元分析，获得相应的缆芯温度数据。预测模型的输入、输出信息见表2，时间间隔控制为1h，共得到700多组原始数据。根据文中的预测方法，借助mapminmax函数对数据实施归一化处理，从原始数据中得到741组样本，前693组是训练集，用于建立预测模型；剩下的样本当作测试集，用来对模型准确性进行检验。

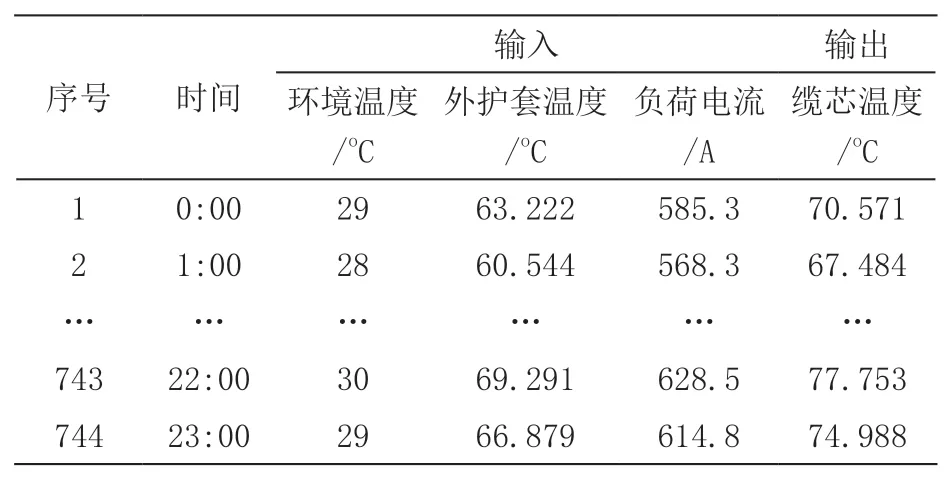
表2 输入及输出数据

通过BP神经网络对缆芯温度进行预测，其真实值和预测值存在较高的拟合度，误差处于[-0.0,0.6]之间来回波动，表明利用这个模型能获得准确地预测温度数值。本次研究挑选均方误差（MSE）、平均绝对误差（MAE）及百分比误差（MAPE）这三个指标，其结果见表3。通过分析，MSE、MAE、MAPE这三个数值均比较小，表明所用温度预测模型具有较高的精度，能够准确预测电力电缆缆芯温度，从而为合理设定缆芯温度预测阀值提供重要的参考。

表3 模型性能评价结果

4 结论

综上所述，电缆是电力传输过程中一种重要的设备，电缆可靠性对电力系统安全、稳定性产生重要的影响。文中利用有限元分析法计算电力电缆温度场，得到相应的电缆缆芯温度样本，在此基础上，建立相应的预测模型。本次研究结果证实，采用有限元与神经网络相结合对电力缆芯温度进行预测，能有效解决缆芯难以直接测量温度的问题，对于预判电缆运行状态、保证电力线路安全运行具有重要的意义。