深埋高地应力隧道不同支护时机求解方法对比研究

蒋长伟， 陈子全, *， 汪 波， 李天胜, ， 周子寒， 包烨明

(1. 西南交通大学 交通隧道工程教育部重点实验室， 四川 成都 610031； 2. 中铁十二局集团有限公司， 山西 太原 030024)

0 引言

在隧道建设过程中，最重视的是初期支护以及二次衬砌对围岩支护的作用。但是实践证明，在应对高地应力环境时，单纯依靠加强支护参数来控制围岩变形的效果并不理想。目前，支护设计理论中最广泛使用的是收敛-约束法，其强调充分发挥围岩的自承载力。选择合理的支护时机是充分发挥围岩自承载力的关键。若支护过早会使围岩应力未最大程度释放，可能会造成支护结构破坏；而支护过晚会造成围岩不稳定，也可能导致支护结构破坏。

已有许多学者对于隧道支护时机进行了大量研究。苏凯等[1]、朱泽奇等[2]对不同支护时机的地下洞室围岩稳定性进行了分析计算。张光伟等[3]对高地应力隧道的初期支护时机进行了研究。白琦等[4]通过建立开挖荷载释放率与监测断面至掌子面距离的关系，确定了以施加支护时监测断面与掌子面的距离为参数的锚固支护时机。陈特等[5]利用位移增量法对支护时机进行研究，认为在测点变形增量显著增加时是最佳支护时机。苏凯等[6]利用塑性区法对支护时机进行研究，认为在开挖边界上出现塑性区时，围岩可能会发生破坏，这时为最晚的支护时机。肖明清等[7]提出对于深埋隧道采用围岩压力代表值作为设计支护力的理念，并对其计算方法与合理性展开研究。Liu等[8]研究了支护强度、支护时间和初始地应力对塑性损伤半径和衬砌受力的影响。Li等[9]为了选择合适的动态加固时机，分析了围岩应力场演化的时间效应，研究了围岩流变影响应力场的演化规律，给出了应力场演化的计算方法，并开发了相应的程序。Yu等[10]推导了基于修正西原模型的非线性流变本构模型，确定了金川矿区实际监测数据及围岩体流变参数，并利用这些数据通过反分析得到最佳二次支护时间。

由此可见，以往的研究大多针对某一特定工况下支护时机的选取方法与原则，对于各种方法在不同地质条件下的适用性还未见探讨。基于此，本文针对硬岩初期支护的合理支护时机进行研究，采用位移增量法、塑性区法和安全系数法分别对某高原深埋高地应力隧道的支护时机进行求解，并对比分析3种求解方法的优劣，选出最合适的求解方法。

1 支护时机求解方法

在实际工程中，围岩变形以及围岩应力重分布并不是短时间内完成的。在不同时机为洞壁施作支护，会影响到围岩的变形和应力重分布，从而也会影响到支护结构的变形和应力大小。支护时机的求解原理均是按照优化围岩变形与受力状态这一思想提出的。为了方便对安全系数法、位移增量法、塑性区法的求解结果进行对比分析，模型统一采用弹塑性模型，假定围岩为均质、各向同性的连续介质，选用统一的围岩参数。

1.1 安全系数法

采用安全系数法求解支护时机的力学模型如图1所示。安全系数法的求解思路是： 在建立隧道开挖模型的过程中，应该在目标断面之前建立支护结构； 建立好模型后(如图1(a)所示)，计算掌子面持续推进过程中的安全系数，进而由安全系数决定支护时机。该方法的求解步骤如下：

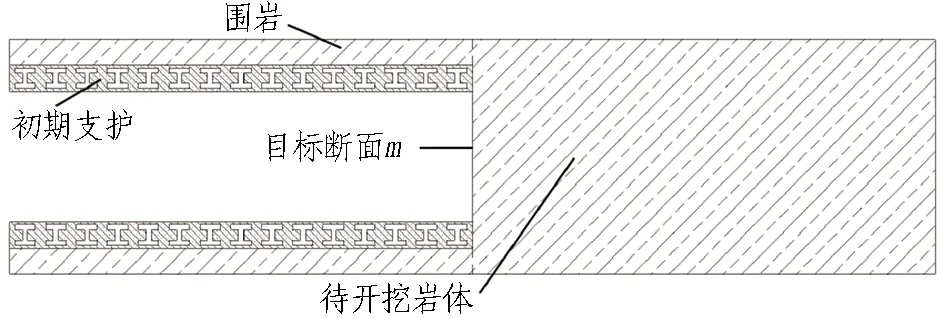
(a) 隧道开挖示意图

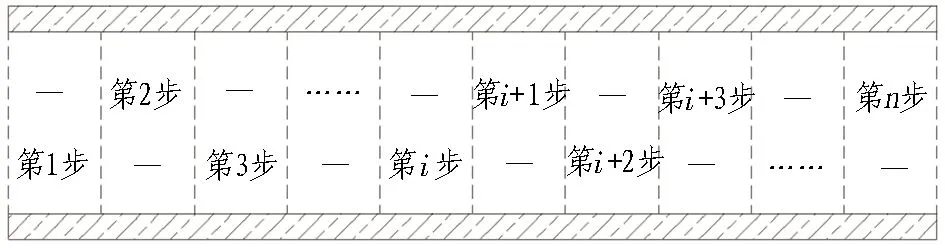
(b) 开挖步骤

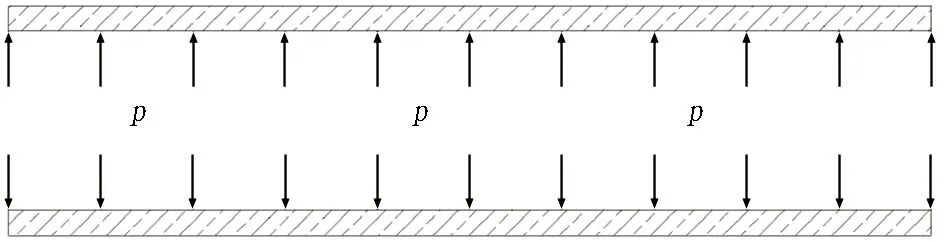
(c) 围岩应力释放

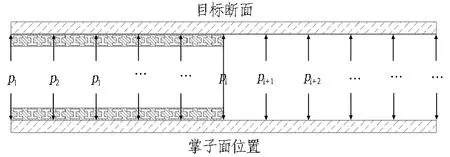
(d) 第1步的虚拟开挖

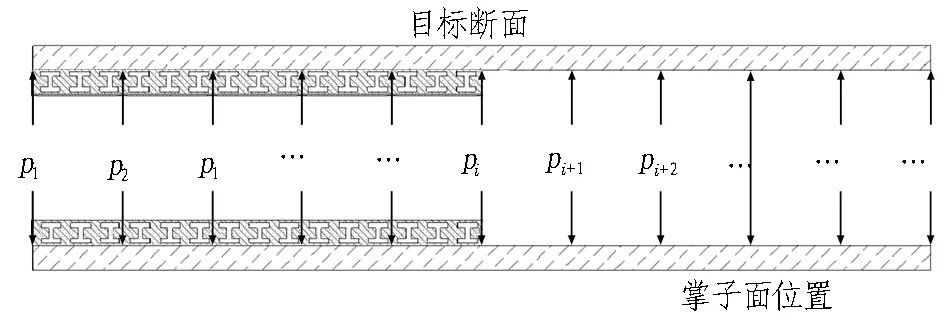
(e) 第n步的虚拟开挖pi为对围岩施加的反力。图1 采用安全系数法求解支护时机的力学模型Fig. 1 Mechanical model of support timing calculated by safety factor method

1)建立好模型后，将实际工况的开挖步距作为每次开挖的距离(如图1(b)所示)，对模型进行开挖求解。选取模型的中间断面为目标断面m，得到掌子面距目标断面的距离x与变形完成率λ的关系曲线，即LDP曲线。

2)通过应力释放法，可以得到围压释放率r与变形完成率λ的关系曲线，即r-λ曲线。

3)创建不含待开挖围岩且在目标断面后方有支护结构的力学模型(如图1(d)所示)，同时不考虑后方支护结构支护时机对目标断面的影响，即后方支护结构为立即施作。通过x-λ曲线找到对应的λ，将对应的λ代入r-λ曲线，即可找到各断面的围压释放率r。这时找到对应的围岩反力p，作用于对应点处，即可复原下一循环的力学状态。其中，p=pg×(1-r)，pg为初始地应力。

4)根据实际开挖顺序向前推进掌子面，掌子面推进一次，就重复一次步骤3)，这样可以模拟掌子面在目标断面m之后任意位置的力学状态(如图1(e)所示)，这时可以得到各断面的变形完成率，再通过r-λ曲线，可以得到各断面对应的围压释放率r，此时再施加对应反力来求解。

通过上述步骤，已经可以将模型中围岩的围压释放率、变形完成率等力学状态复原到与实际状态一致。具体的支护体系支护时机选择过程如图2所示。

基于Mohr-Coulomb屈服准则，工程研究人员提出了岩体单元安全系数F[11]，其计算公式为

(1)

式中：c为黏聚力；φ为内摩擦角；σ1、σ3分别为第一、三主应力。

当F>1时，表明单元体处于弹性状态； 当F<1时，表明单元体处于塑性屈服状态； 当F=1时，表明单元体处于临界失稳状态。

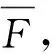
整体安全系数计算完成后，可以得到掌子面距目标断面的距离与整体安全系数的关系曲线(如图2所示)。根据实际工况，将安全系数为l时作为最晚支护时机的指标。此时，将掌子面距目标断面的距离除以每日开挖进度即可得到支护时间t。

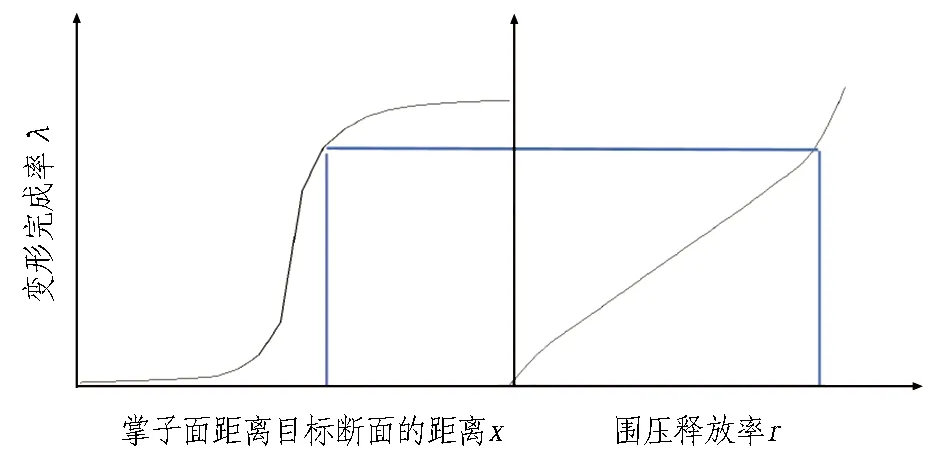
(a) x-λ曲线与r-λ曲线

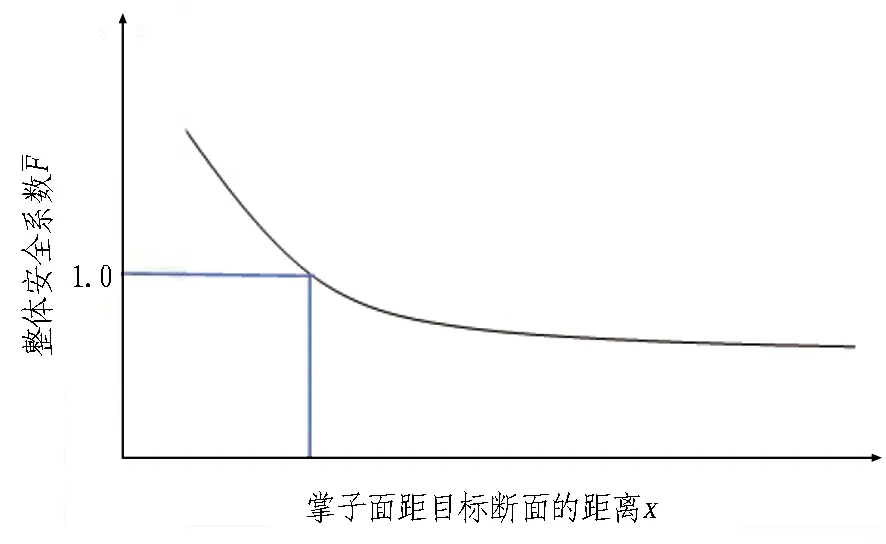
(b) 曲线图2 支护体系支护时机选择过程图Fig. 2 Selection process of support timing of support system

(2)

式中：x为掌子面距目标断面的距离；v为掘进速度。

1.2 位移增量法

在隧道开挖过程中，监测围岩位移，当围岩位移变化速率过快时，围岩很有可能出现失稳。为了防止围岩失稳，应及时施作支护结构。

采用位移增量法求解的具体步骤如下：

1)建立好模型后，通过应力释放法可以得到围岩应力的释放率与位移增量的关系曲线。首先，将待开挖部分的围岩去除，根据释放系数将得到的开挖荷载等效节点力按比例分为10份(每份10%)，依次施加，分别统计各开挖荷载释放率下各个测点的位移； 然后，将相邻的位移量做差值，得到围岩应力的释放率与位移增量的关系曲线。通过该关系曲线可以知道应力释放10%时位移增量的变化。此时，位移增量反映的是位移随着应力释放率增长的速率，假设位移增量在每一份10%应力释放率之间是均匀变化的，那么当位移增量显著增加时，应施作支护，防止围岩失稳。

2)考虑到在实际工程中无法直接参考围压释放率进行分析，需要将围压释放率转换成供实际工程参考的参数。通过掌子面效应可以得到掌子面距目标断面的距离与变形完成率的关系曲线，然后将采用应力释放法得到的围压释放率与变形完成率的关系曲线与之对应，即可得到相应的围压释放率下掌子面距目标断面的距离，该参数可以直接运用在实际工程中。

1.3 塑性区法

在隧道开挖过程中，由于开挖时会卸载，会导致开挖的周边围岩局部进入塑性区。随着塑性区的发展，围岩会越来越容易失稳。所以当围岩出现塑性区时，应该及时施作支护结构。

采用塑性区法求解的步骤如下：

1)建立好模型后，将实际工况的开挖步距作为每次开挖推进的距离，对模型进行一步一步地开挖求解，保存每一步的求解模型，选取模型的中间断面为目标断面。

2)提取每一次目标断面的塑性区云图进行分析，观察目标断面塑性区的发展规律。假设出现塑性区时围岩可能会发生破坏，即目标断面塑性区开始发展时，就应在目标断面上施加支护结构，以此时掌子面距目标断面的距离作为支护时机选择的参考。

2 工程背景与计算工况

2.1 工程背景

依托的高原深埋高地应力隧道位于四川盆地与青藏高原过渡的西南边缘。受多水系的强烈切割，隧址区地形高差大，沟壑密布，山岭纵横，且林木茂密、气候温润，带有典型的亚热带温湿谷地特征。地表高程3 460～4 730 m，外营力以冰水侵蚀作用、冻融作用为主，同时伴有生物风化等作用，为典型高原地貌。隧道横洞的最大埋深约1 215 m，长度为1 854 m，区段为深切峡谷地貌，地形起伏较大，主要岩性为花岗岩，岩石节理弱发育，完整性较好。

2.2 计算工况

选取先期开工的横洞埋深600 m处作为目标断面，同时考虑高地应力条件下不同埋深对支护时机的影响，设计了另外2种埋深的计算工况。每种计算工况的围岩物理力学参数如表1所示。根据薛玺成等[12]提出的当围岩第一主应力大于20 MPa时可定义为高地应力，3种工况下围岩的第一主应力均大于20 MPa，符合高地应力条件。

表1 各计算工况围岩物理力学参数Table 1 Physico-mechanical parameters of surrounding rock under each calculation condition

利用Flac3D软件建立某高原深埋高地应力隧道三维数值模型(如图3(a)所示)，模型尺寸为100 m×92.5 m×82.5 m(长×宽×高)，隧道跨度约9.26 m，高约8.26 m。三维模型共计138 363个节点、131 200个单元，在模型纵向中间位置(即50 m处)设置了目标监测断面。在模型底面及侧面施加法向位移约束，在顶面施加与埋深对应的自重荷载，在4个侧面施加对应的侧压力系数，恢复初始地应力状态后得到初始地应力模型。监测断面上临空面的围岩单元共计52个，编号如图3(b)所示。

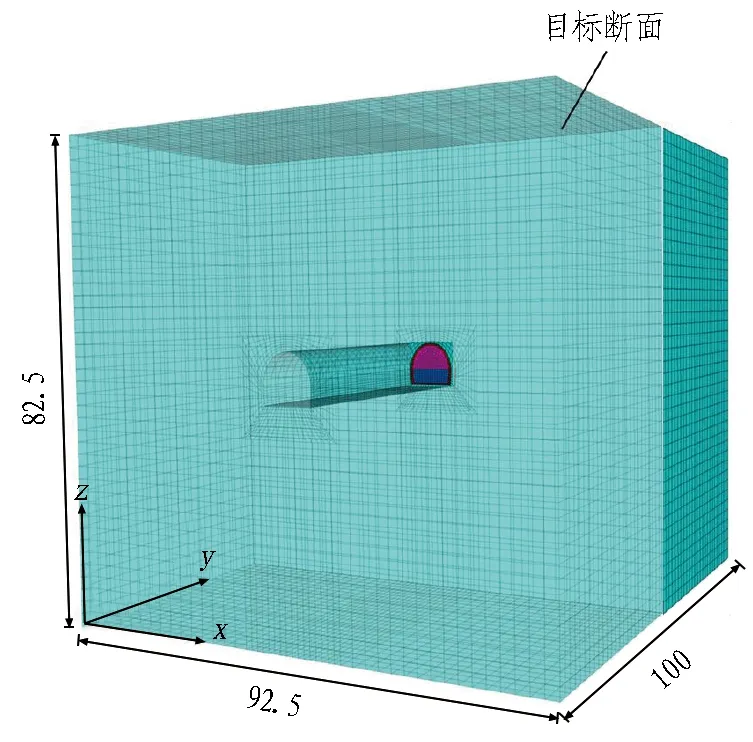
(a) 三维计算模型

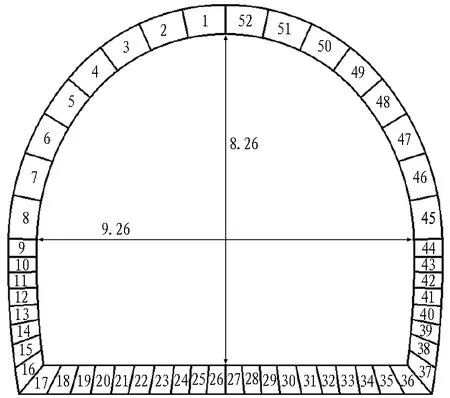
(b) 监测断面单元编号图3 深埋高地应力隧道三维计算模型(单位： m)Fig. 3 Three-dimensional calculation model of a deep-buried plateau tunnel(unit： m)

3 支护时机求解

3.1 安全系数法求解

3.1.1 LDP曲线分析

某高原深埋高地应力隧道每天平均掘进2 m，则模型每次开挖距离为2 m。记录每次开挖后目标断面距掌子面的距离及对应的变形完成率，最后得到LDP曲线，如图4所示。

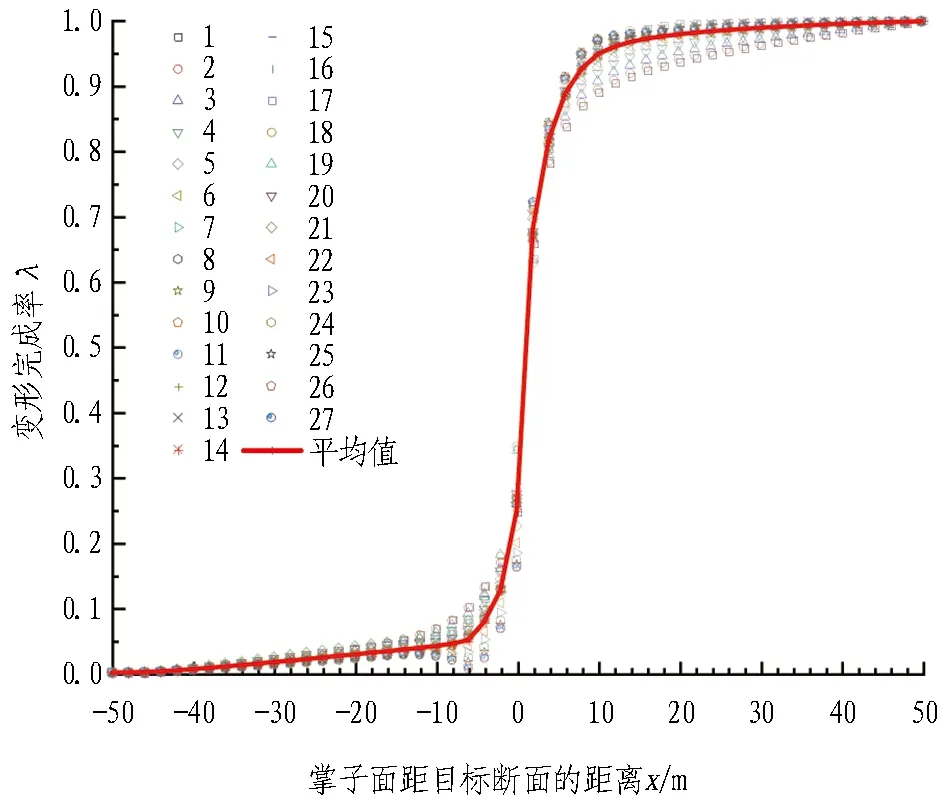
(a) 工况1

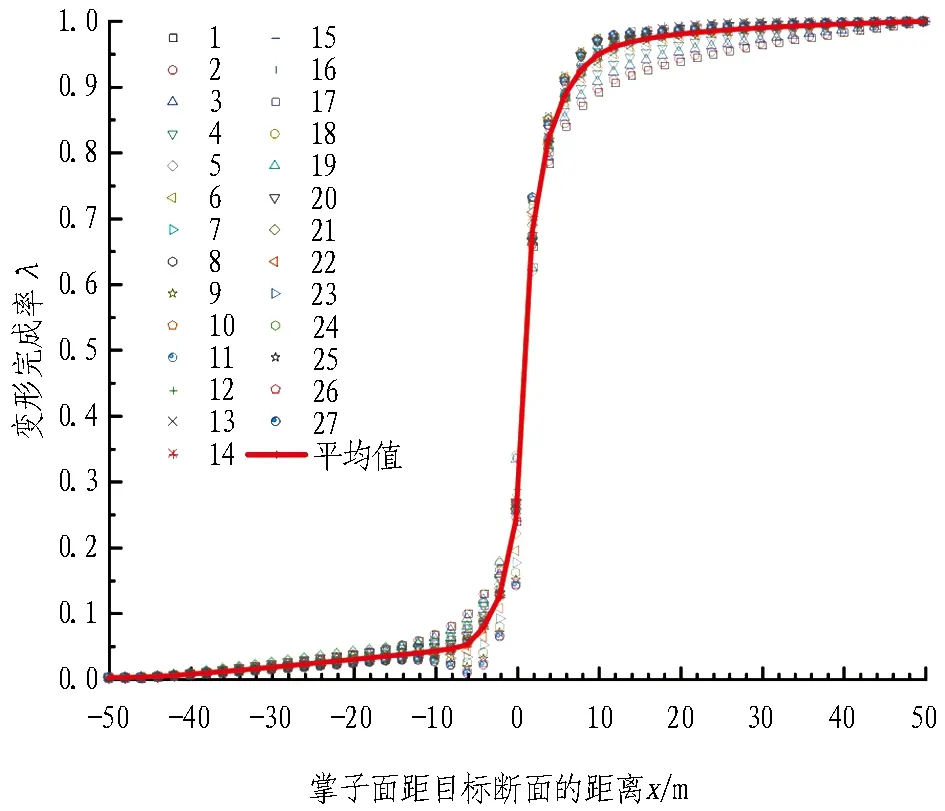
(b) 工况2

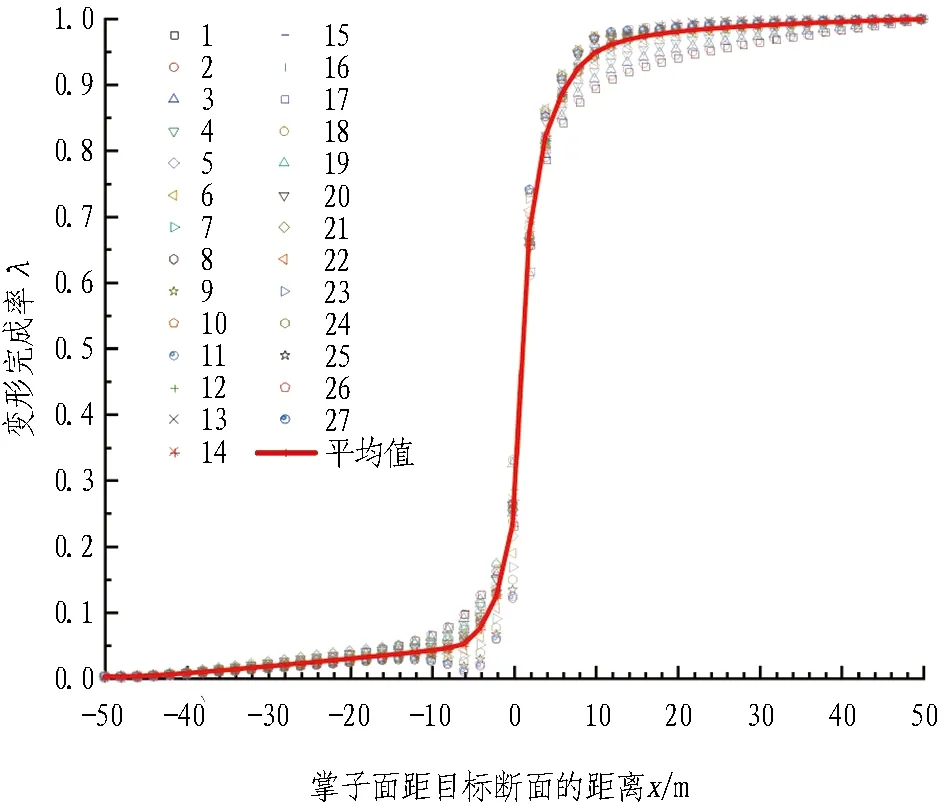
(c) 工况3图4 各工况下的LDP曲线Fig. 4 LDP curves of longitudinal distribution of surrounding rock displacement in various conditions

工况1的LDP曲线如图4(a)所示。当掌子面位于目标断面(x=0 m)之前时，目标断面的平均位移约占最终平均位移的24.8%； 掌子面推进至目标断面后4～6 m，变形完成率近乎线性增长，由0.26增长至约0.89； 之后LDP曲线出现反弯，变形完成率增长速率减小。

工况2的LDP曲线如图4(b)所示。当掌子面位于目标断面(x=0 m)之前时，目标断面的平均位移约占最终平均位移的24.1%； 掌子面推进至目标断面后4～6 m，变形完成率近乎线性增长，由0.24增长至约0.89； 之后LDP曲线出现反弯，变形完成率增长速率减小。

工况3的LDP曲线如图4(c)所示。当掌子面位于目标断面(x=0 m)之前时，目标断面的平均位移约占最终平均位移的23.1%； 掌子面推进至目标断面后4～6 m，变形完成率近乎线性增长，由0.23增长至约0.88； 之后LDP曲线出现反弯，变形完成率增长速率减小。

由上述可知，3种工况下的变形完成率变化规律较为相似，随着埋深的增加，各点的变形完成率分布也较为集中。

3.1.2 整体变形完成率分析

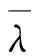
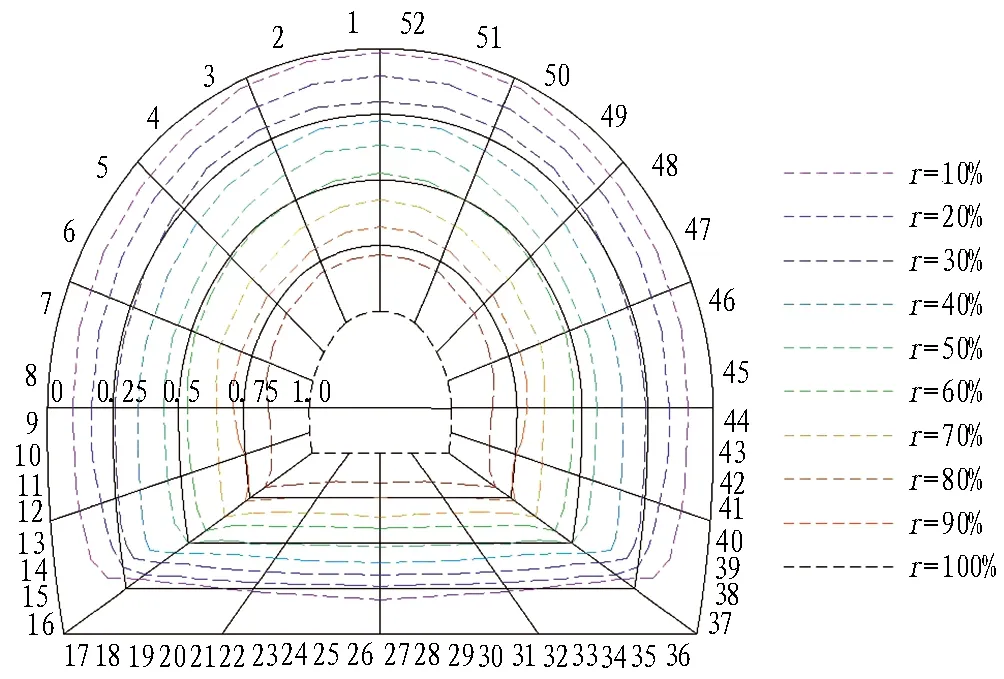
图5 临空面上各节点变形完成率随围压释放率的变化规律Fig. 5 Displacement completion coefficient of each point on free surface with stress release rate

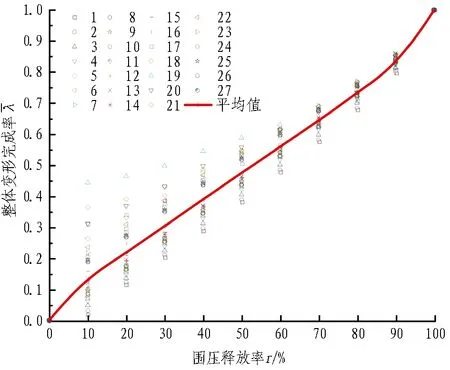
(a) 工况1

(b) 工况2

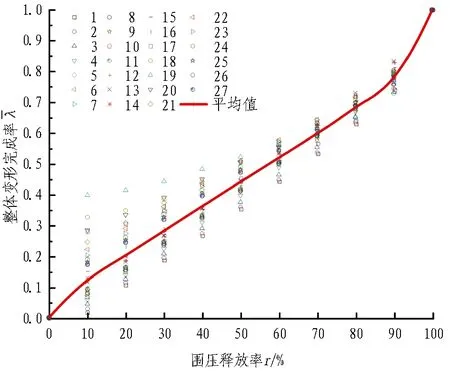
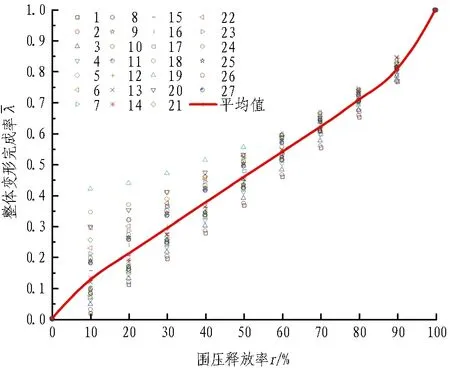
(c) 工况3图6 整体变形完成率随围压释放率的变化规律Fig. 6 Overall displacement completion coefficient with stress release rate

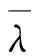
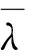
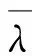
由上述分析可知，3种工况下围压释放率与整体变形完成率的关系曲线变化规律基本相同，且在整体变形完成率与围压释放率呈线性关系快结束时围压释放率均为70%。不同的是，此时整体变形完成率随着埋深的增加而减小，并且随着埋深的增加，各点的整体变形完成率也相对收敛。

3.1.3 安全系数分析

依据1.1节中支护时机的确定方法，分析围岩安全系数的演变过程，找到合理的支护时机。工况1围岩安全系数随掌子面推进的变化规律如图7所示。工况1侧压力系数为1.4和1.0，所以原围岩应力以构造应力场为主导，掌子面从目标断面开始开挖后，目标断面的临空面上呈现拱腰和拱脚的安全系数较大、拱顶和仰拱的安全系数相对较小的现象。随着掌子面持续推进，临空面上各点的安全系数逐渐减小，而拱脚处的安全系数一直大于1，则可以认为，随着掌子面的推进拱脚处一直处于安全范围。因此，在计算整体安全系数时，不考虑拱脚处的安全系数对整体安全系数的影响，这时的整体安全系数可以更准确地描述围岩临空面的危险程度，进而更准确地确定支护时机。

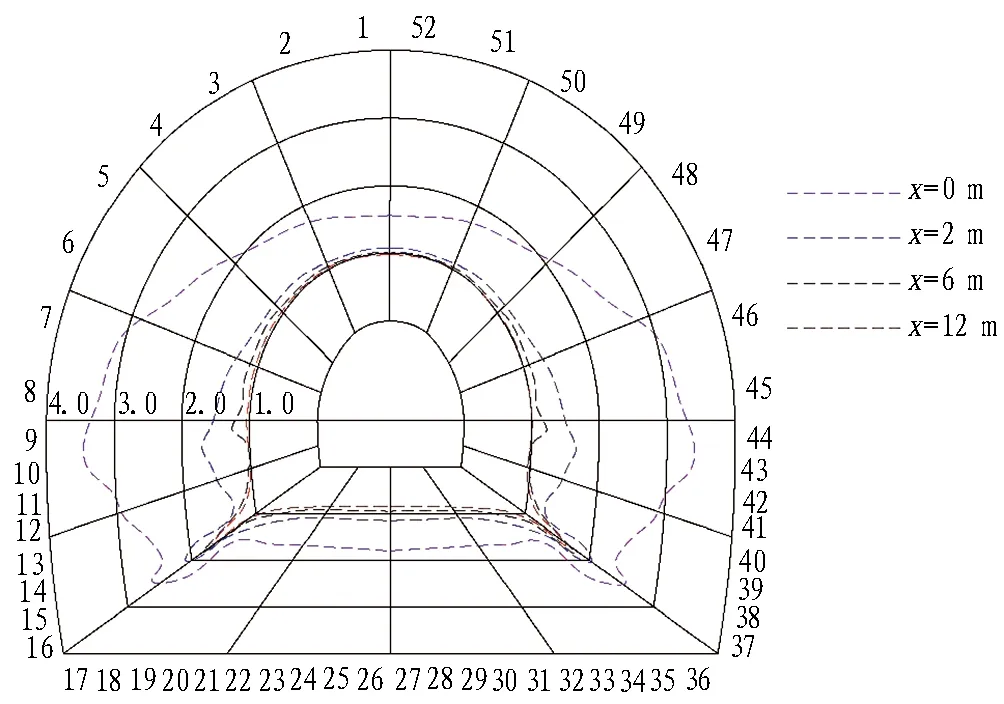
图7 工况1围岩安全系数随掌子面推进的变化规律Fig. 7 Safety coefficient of surrounding rock with advancement of tunneling face in condition 1

工况1支护时机参数确定对照图如图8(a)所示。由图8(a)可以确定安全系数F=1时对应的最晚支护时机是掌子面距目标断面后6.0 m。考虑到开挖速率为2 m/d，即最晚应在3 d后施作初期支护。同时，由图8(a)可确定最晚支护时机目标断面对应的围压释放率r与变形完成率λ。

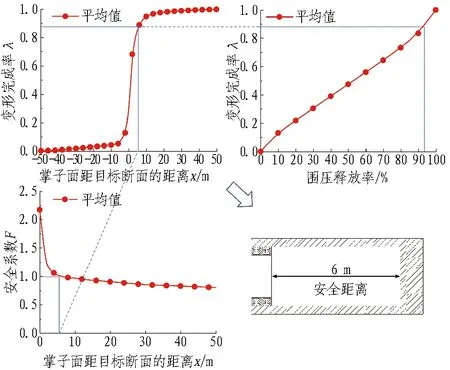
(a) 工况1

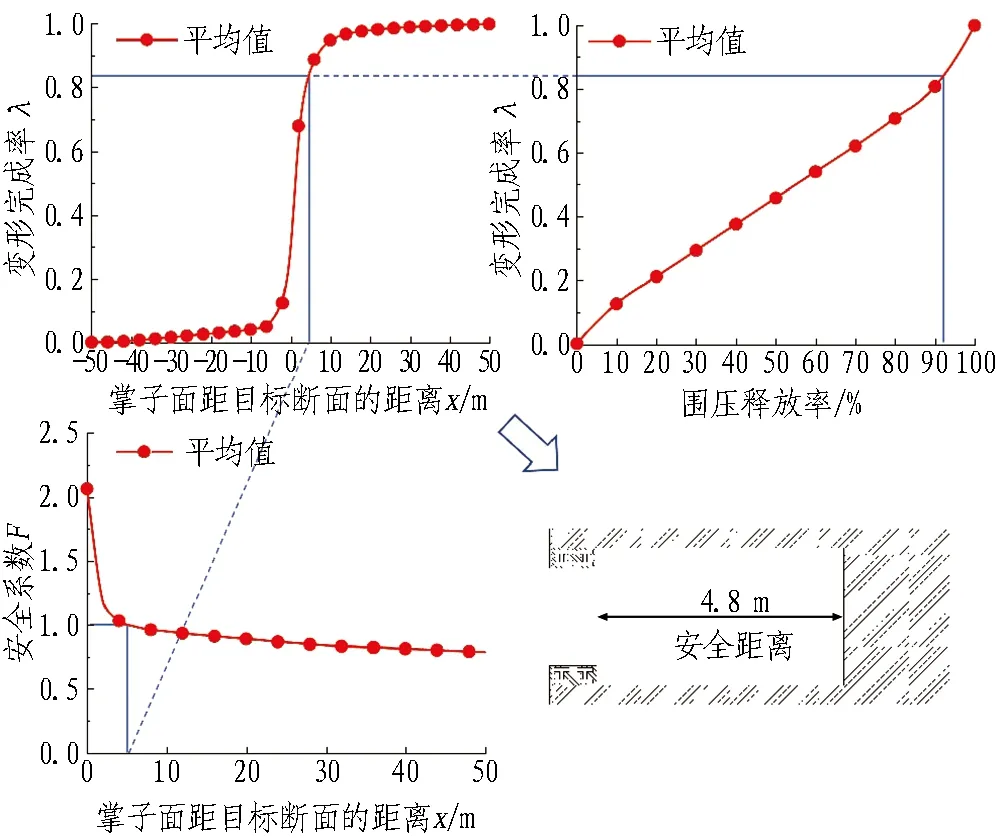
(b) 工况2

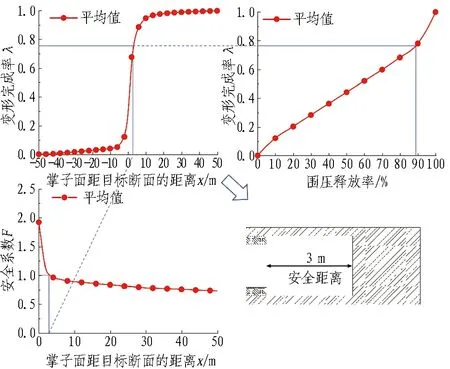
(c) 工况3图8 支护时机参数确定对照图(安全系数法)Fig. 8 Parameters control of support timing determination (safety factor method)

用同样的方法可以确定工况2和工况3的安全系数变化规律。工况2和工况3中临空面上各点的安全系数变化规律与工况1相似，拱脚处的安全系数也始终大于1，所以计算整体安全系数时，同样不考虑拱脚处的安全系数对整体安全系数的影响。工况2和工况3支护时机参数确定对照图分别如图8(b)和图8(c)所示。对于工况2，由图8(b)可以确定安全系数F=1时对应的最晚支护时机是掌子面距目标断面后4.8 m。考虑到开挖速率为2 m/d，即最晚应在2.4 d后施作初期支护。同时，从图8(b)中可确定最晚支护时机目标断面对应的围压释放率r与变形完成率λ。对于工况3，由图8(c)可以确定安全系数F=1时对应的最晚支护时机是掌子面距目标断面后3.0 m。考虑到开挖速率为2 m/d，即最晚应在1.5 d后施作初期支护。同时，从图8(c)中可确定最晚支护时机目标断面对应的围压释放率r与变形完成率λ。

3.2 位移增量法求解

同样，将初始围岩应力平均分成10份，每次按10%进行释放，记录目标断面各节点的位移增量。位移增量随围压释放率的变化规律如图9所示。

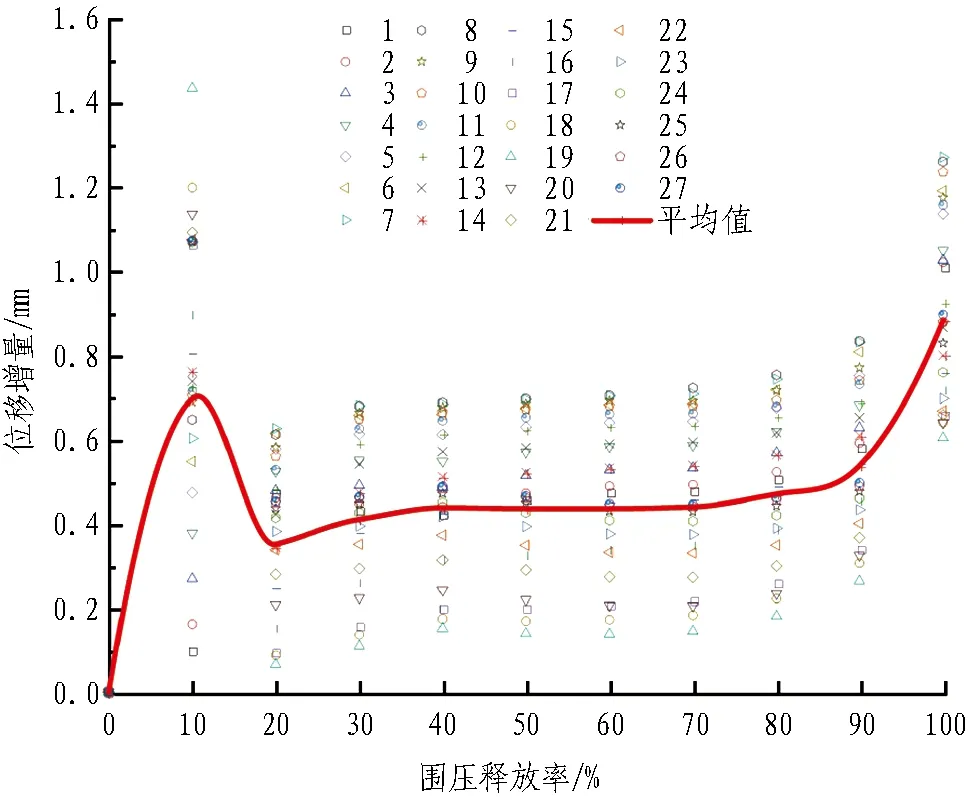
(a) 工况1

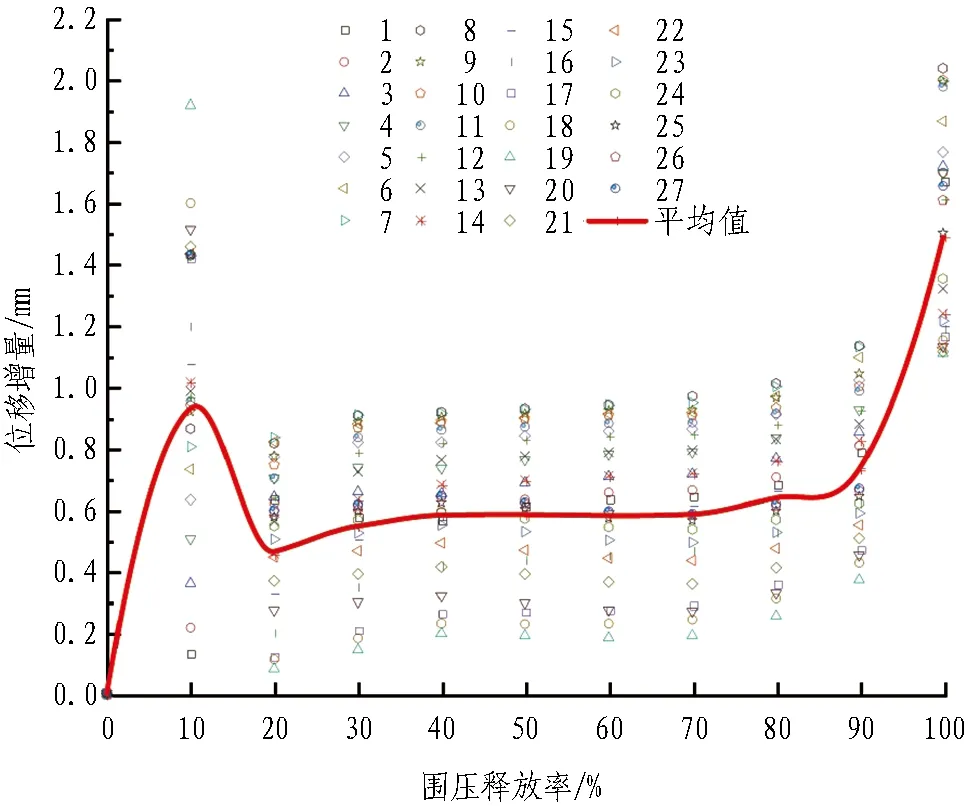
(b) 工况2

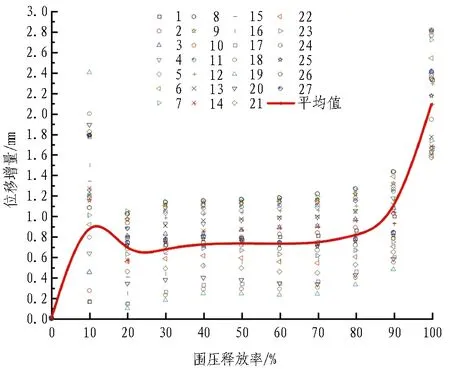
(c) 工况3图9 位移增量随围压释放率的变化规律Fig. 9 Displacement increment with stress release rate

对于工况1，由图9(a)可知，除了最开始释放的20%的应力，在围压释放率达到70%之前，位移增量几乎是固定不变的，在r=70%时位移增量约为0.44 mm，此后位移增量开始随着围压释放率的增加而增大。所以，在r=70%之前应该施作支护。

对于工况2，由图9(b)可知，除了最开始释放的20%的应力，在围压释放率达到70%之前，位移增量几乎是固定不变的，在r=70%时位移增量约为0.59 mm，此后位移增量开始随着围压释放率的增加而增大。所以，在r=70%之前应该施作支护。

对于工况3，由图9(c)可知，除了最开始释放的20%的应力，在围压释放率达到70%之前，位移增量几乎是固定不变的，在r=70%时位移增量约为0.73 mm，此后位移增量开始随着围压释放率的增加而增大。所以，在r=70%之前应该施作支护。

根据上述分析可知，3种工况下围压释放率与位移增量的关系曲线变化规律大致相同，且位移增量保持基本不变的最大围压释放率均为70%。不同的是，在相同围压释放率的情况下，位移增量随着埋深的增加而增大。

各工况支护时机参数确定对照图如图10所示。

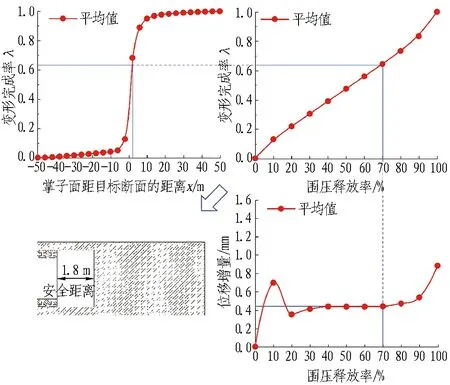
(a) 工况1

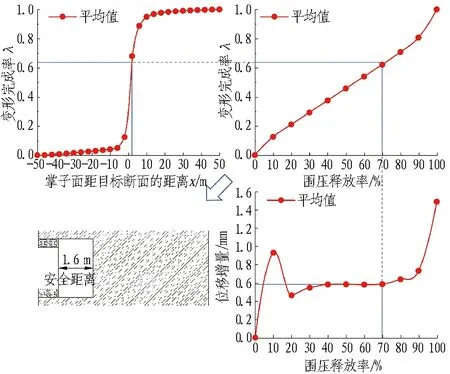
(b) 工况2

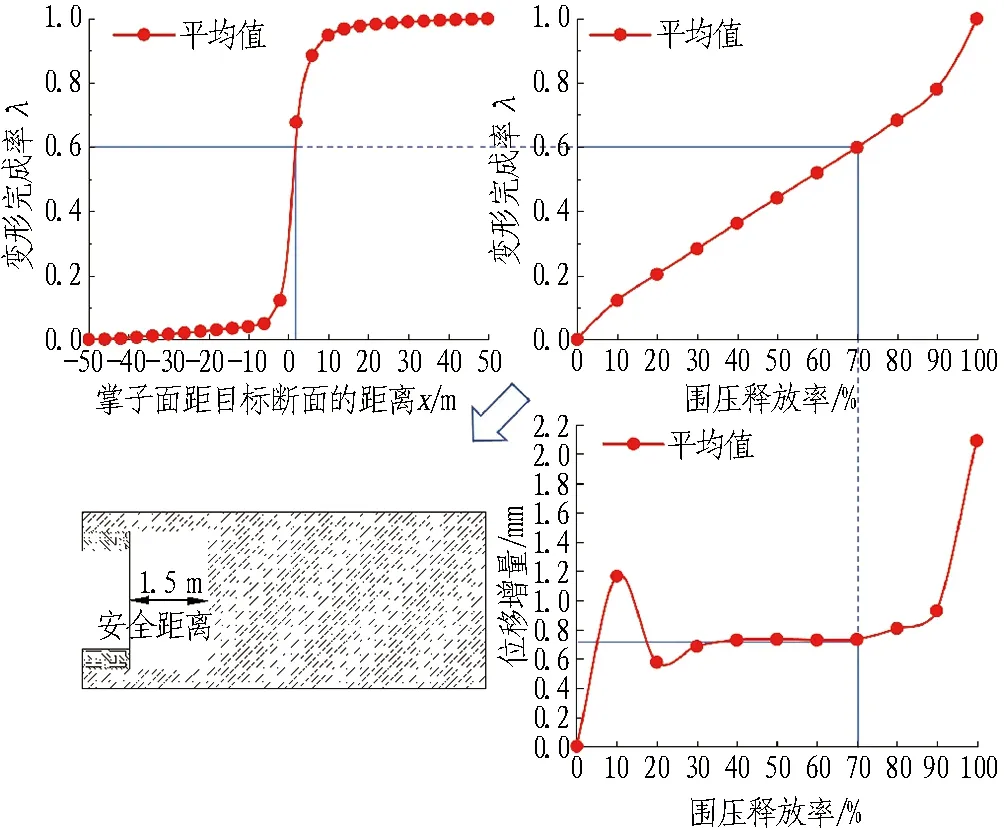
(c) 工况3图10 各工况支护时机参数确定对照图(位移增量法)Fig. 10 Parameters control of support timing determination in each condition (displacement increment method)

对于工况1，图10(a)确定了围压释放率为70%时对应的最晚支护时机是掌子面距目标断面后1.8 m。考虑到开挖速率为2 m/d，即最晚应在0.9 d后施作初期支护。同时，从图10(a)中可确定最晚支护时机目标断面对应的围压释放率与变形完成率。

对于工况2，图10(b)确定了围压释放率为70%时对应的最晚支护时机是掌子面距目标断面后1.6 m。考虑到开挖速率为2 m/d，即最晚应在0.8 d后施作初期支护。同时，从图10(b)中可确定最晚支护时机目标断面对应的围压释放率与变形完成率。

对于工况3，由图10(c)确定围压释放率为70%时对应的最晚支护时机是掌子面距目标断面后1.5 m。考虑到开挖速率为2 m/d，即最晚应在0.75 d后施作初期支护。同时，从图10(c)中可确定最晚支护时机目标断面对应的围压释放率与变形完成率。

3.3 塑性区法求解

同样，将初始围岩应力平均分成10份，每次按10%进行释放，对每次释放完应力的模型进行求解保存。提取每个求解模型在目标断面的塑性区云图，通过对比分析云图，找到最开始发展塑性区的位置。各工况下围压释放率为80%时的围岩塑性区云图如图11所示。

(a) 工况1

(b) 工况2

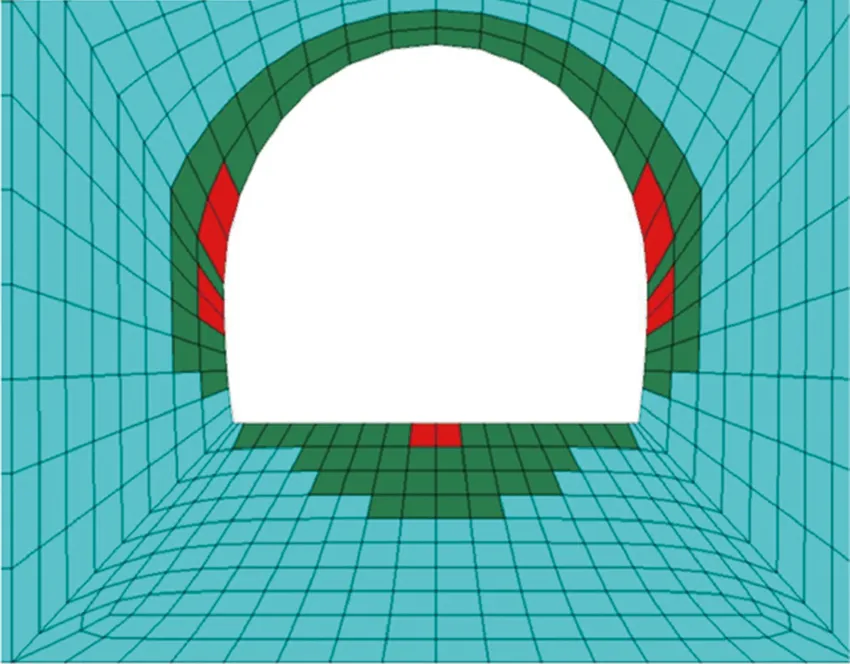
(c) 工况3图11 各工况下围压释放率为80%时的围岩塑性区云图Fig. 11 Plastic zone with a stress release rate of 80% in each condition

对于工况1，当围压释放率为80%时，洞壁开始出现塑性区，拱顶、拱肩以及仰拱最早进入塑性阶段。

对于工况2，在围压释放率为80%时，洞壁开始出现塑性区，最早出现塑性区的地方是拱顶、拱肩以及仰拱，仰拱塑性区深度较大。

对于工况3，在围压释放率为80%时，洞壁开始出现塑性区，最早出现塑性区的地方是拱顶、拱肩以及仰拱，拱腰和仰拱均有拉伸产生的塑性区。

由分析可知，3种工况下均是在围压释放率为80%时，洞壁开始出现塑性区，并且出现塑性区的位置均是拱顶、拱肩以及仰拱。不同的是，从工况1到工况3，随着埋深的增加，在围压释放率相同的情况下，各处的塑性区范围在逐渐扩大。

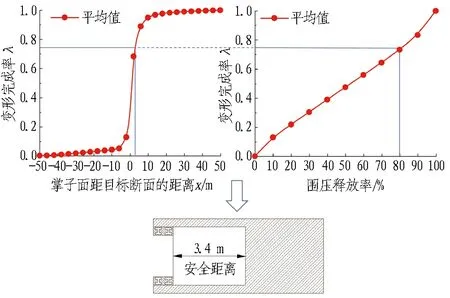
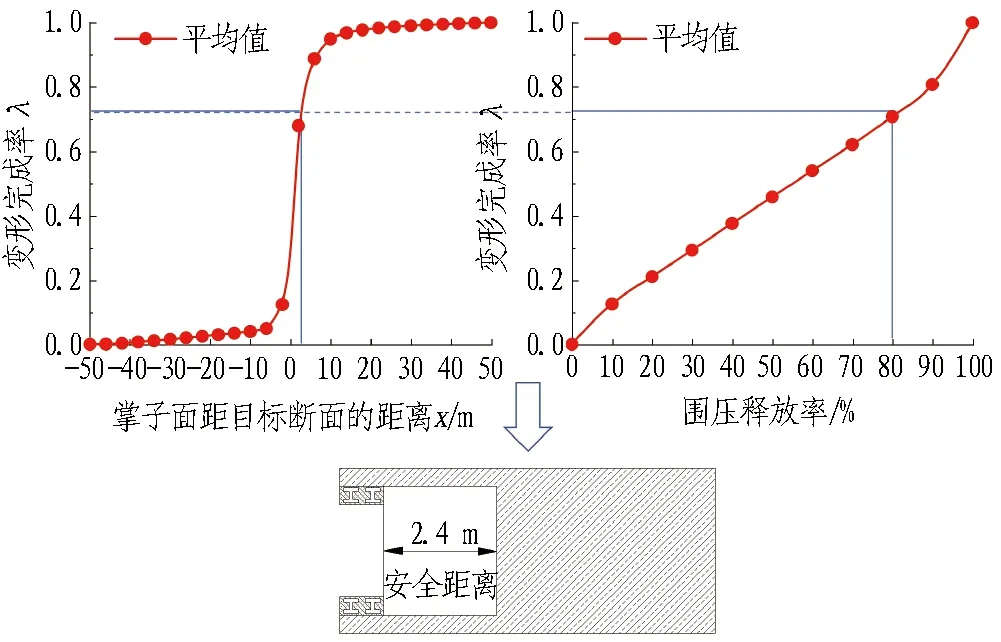
各工况支护时机参数确定对照图如图12所示。

(a) 工况1

(b) 工况2

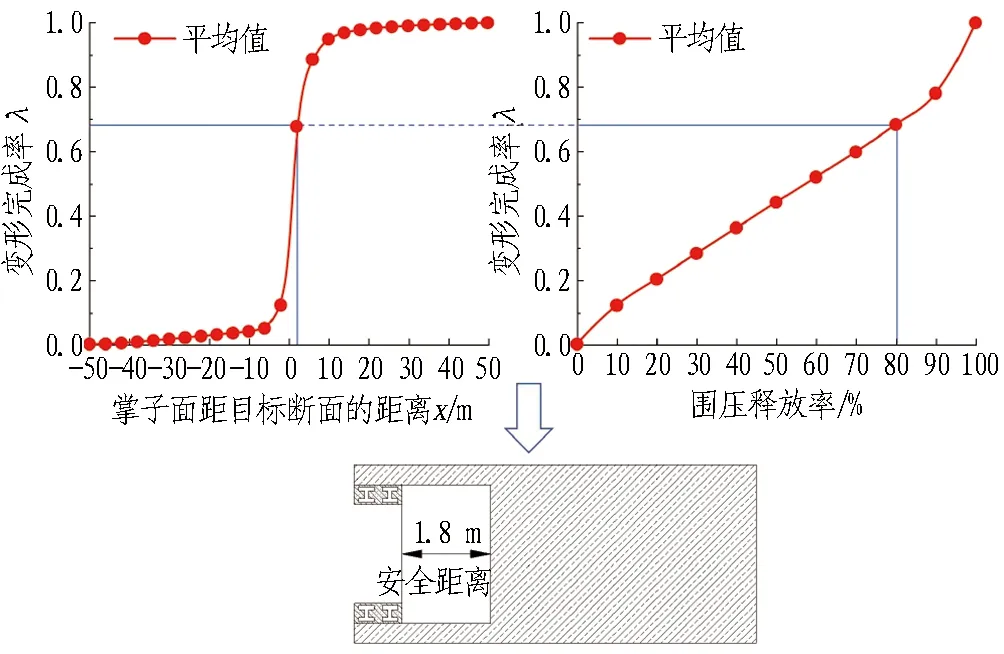
(c) 工况3图12 各工况支护时机参数确定对照图(塑性区法)Fig. 12 Parameters control of support timing determination in each condition (plastic zone method)

由图12(a)可知，对于工况1，在围压释放率为80%时对应的最晚支护时机是掌子面距离目标断面3.4 m。考虑到开挖速率为2 m/d，即最晚应在1.7 d后施作初期支护。同时，从图12(a)中可确定最晚支护时机目标断面对应的围压释放率与变形完成率。

由图12(b)可知，对于工况2，在围压释放率为80%时对应的最晚支护时机是掌子面距离目标断面2.4 m。考虑到开挖速率为2 m/d，即最晚应在1.2 d后施作初期支护。同时，从图12(b)中可确定最晚支护时机目标断面对应的围压释放率与变形完成率。

由图12(c)可知，对于工况3，在围压释放率为80%时对应的最晚支护时机是掌子面距离目标断面1.8 m。考虑到开挖速率为2 m/d，即最晚应在0.9 d后施作初期支护。同时，从图12(c)中可确定最晚支护时机目标断面对应的围压释放率与变形完成率。

4 不同方法求解结果对比

通过对3种支护时机求解方法进行对比，可以得到同样条件下，采用安全系数法求解得到的支护时机晚于塑性区法，而采用塑性区法求解得到的支护时机晚于位移增量法。

4.1 求解原理分析

由于本文所选用的模型为弹塑性模型，而弹塑性模型的基本概念是： 岩石在屈服极限之前只有可恢复的弹性变形，达到屈服极限以后，变形将分成可恢复的弹性变形和不可恢复的塑性变形[13]。位移增量法是根据位移的变化速率来决定支护时机，塑性区法是洞壁出现塑性区时进行支护，安全系数法是屈服面上发生剪切破坏时进行支护。而当围岩从弹性阶段进入到屈服阶段时，同等的应力变化将会导致更大的位移，同时也会开始出现塑性区。所以这3种方法是基于岩石开始发生屈服所确定的支护时机。

4.2 不同点对比分析

3种方法的假设都包括了模型采用弹塑性模型，围岩为均质、各向同性的连续介质，对应工况的围岩参数相同。3种方法的应用条件均为高地应力硬岩条件。不同的是，安全系数法包括了创建不含待开挖围岩且在目标断面后方有支护结构的力学模型，同时不考虑后方支护结构支护时机对目标断面的影响，以及安全系数1为失稳的界限； 位移增量法包括了位移增量反映的是位移随着应力释放率变化的增长速率，假设位移增量在每份10%应力释放率之间是均匀变化的； 塑性区法是假设出现塑性区时，围岩可能会发生破坏，即目标断面塑性区开始发展时应施加支护结构。

4.3 工程类比

对埋深2 000 m的硬岩隧道，文献[14]选取的隧道支护时机是围压释放率为90%时。对于埋深700 m的页岩、粉质砂岩和泥岩隧道，文献[15]选取的支护时机是安全距离为4 m时。对于埋深1 000 m的软岩隧道，文献[16]选取的最晚支护时机是安全距离为5 m时。对于埋深570 m的木寨岭隧道2#斜井，文献[3]给出的内层初期支护时机为外层钢拱架施作7.2～14.4 m时。对于高地应力引水隧洞，文献[17]给出的支护滞后距离为3～6 m。根据上述文献对支护时机的选择，可见采用安全系数法求得的支护时机更加符合工程实际，而位移增量法和塑性区法相对于安全系数法来说过于保守，使用安全系数法来计算支护时机可以将支护时机适当延后。这样在保证施工安全的同时，也可减小施作支护后支护结构的受力。

5 结论与展望

本文依托某高原深埋高地应力隧道，对安全系数法、位移增量法和塑性区法3种方法求解得到的支护时机进行了分析，得出的主要结论如下。

1)3种工况下某高原深埋高地应力隧道横洞Ⅲ级围岩拱腰和拱脚的安全系数相对于拱顶和仰拱大，这是由于高地应力造成的，同时说明拱腰和拱脚较为安全，拱顶和仰拱容易发生破坏。对于塑性区法，3种工况的塑性区分布规律是相同的，均是拱顶和仰拱处最早产生塑性区，所以拱顶和仰拱处容易发生破坏。对于位移增量法，3种工况的位移增量分布规律是相同的，其中，拱顶和仰拱处的位移增量较大，而拱腰和拱脚处的位移增量较小。这说明采用3种方法都能得到仰拱和拱顶容易发生破坏而拱腰和拱脚相对不容易破坏的结果。

2)采用安全系数法求解得到3种工况的最晚支护时机(按照安全距离进行对比)分别是掌子面距离目标断面6.0、4.8、3.0 m； 采用位移增量法求解得到3种工况的最晚支护时机分别是掌子面距离目标断面1.8、1.6、1.5 m； 采用塑性区法求解得到3种工况的最晚支护时机分别是掌子面距离目标断面3.4、2.4、1.8 m。采用3种方法得到的规律均是隧道埋深越大，安全距离越短，需要更早施作支护。

3)对比同一工况下3种方法的支护时机求解结果发现，采用安全系数求解得到的安全距离大于采用塑性区法求解得到的安全距离，采用塑性区法求解得到的安全距离大于采用位移增量求解得到的安全距离。在支护时机的求解上，塑性区法和位移增量法相对于安全系数法较为保守。因此，实际工程中可以采用安全系数法进行支护时机求解，以得到更为合理的支护时机。

支护时机的确定对隧道工程的工期、质量和成本控制都有非常重要的影响。本文所使用的本构模型仅适用于硬岩地层，而不适用于软岩地层。但若找到匹配实际工况的本构模型，3种求解支护时机的方法也同样适用于软岩地层。