特长引水隧洞洞内横向贯通精度仿真计算和分析

杨 惠， 高 兵， 谢先武， 刘成龙

(1. 西南交通大学地球科学与环境工程学院， 四川 成都 611756； 2. 中铁十一局集团第五工程有限公司， 重庆 400037)

0 引言

引水隧洞作为一种促进水资源合理配置的水工隧洞[1]，一般具有距离长、深埋大[2]等特点，因此，在隧道施工开挖时会面临测量误差累积所引起的横向摆动大、隧道难以准确贯通等问题。为了实现特长引水隧洞的顺利贯通，可以采取的一个主要技术措施是优化洞内平面控制网网形及其测量方法。

长大隧道洞内平面测量一般采用双导线环网或菱形交叉导线网[3]。其中，交叉导线网结构稳定性强[4]，在一定程度上可以控制带状控制网的横向摆动，为了进一步提升洞内整网的网形强度，考虑在交叉导线网的基础上，于进洞处和斜井与主洞交汇处的平面联系测量中加测若干个自由测站的边角观测值，组成一种混合固定测站和自由测站观测值的隧道洞内平面控制测量新网形。为探究采用新网形进行洞内平面控制测量的精度情况，需要估算洞内横向贯通误差。传统的贯通误差预计方法(图解法或解析法)需要人工量取设计图纸，效率低下[5]。张正禄等[6]、付宏平等[7]曾利用计算机模拟方法估算不同长度隧道的贯通精度，从而建设性地提出了20～50 km隧道横向贯通误差允许值； 马骥等[5]利用基于蒙特卡洛原理的模拟方法预计某沉管隧道贯通误差，取得了良好的应用效果。然而，目前多数学者在模拟观测值时添加的模拟误差为以平面测量等级规定的限差值作为标准差生成的伪随机数，并且模拟的多为相向开挖的直线型隧道，网形中控制点纵横向间距完全相等。显然，无论是观测误差还是洞内平面网形，都与实际测量情况存在一定差异。

本文根据新疆某特长引水隧洞实际走向，模拟混合固定测站和自由测站观测值的洞内平面控制测量网形，按照隧道二等要求和实测数据统计的边角观测精度生成模拟误差并进行仿真计算，从而预计横向贯通精度，再按该仿真模拟网形对该特长引水隧洞洞内平面控制网进行布网及施测，以验证该网形能否满足隧道二等的精度要求和能否顺利贯通，最后将仿真计算结果与实测结果进行对比分析，从而验证本文仿真计算方法的可行性和可靠性，并确保采用仿真计算网形施测的该特长引水隧洞洞内平面控制网的精度。

1 仿真计算方法及仿真计算试验

1.1 洞内平面控制网精度仿真计算原理

特长隧道洞内平面控制网精度仿真计算，实际上是一种估算洞内平面控制网精度及其横向贯通误差的新方法。与常用的解析法[5]不同，该方法是利用计算机生成洞内平面控制网的设计网形，计算设计网形中各个控制点的设计坐标，利用相邻控制点的设计坐标反算相邻控制点间的边角观测值的设计值[8]； 然后，对该设计值添加符合一定离散度(中误差)的伪随机数，通过数学变换使这些伪随机数的精度指标与实际观测误差基本相符，从而构造出一系列与洞内平面控制网实测值等效的模拟观测值； 最后，利用这些模拟观测值对洞内仿真的平面控制网进行平差处理及精度评定，从而达到预计洞内平面控制网精度和横向贯通误差的目的[9]，其实现步骤主要包括生成伪随机数和构造模拟观测值。

1.1.1 生成服从正态分布的伪随机数

为了模拟服从正态分布的观测误差，首先利用计算机随机数发生器[10-11]，生成一组相互独立且服从[0,1]均匀分布的伪随机数序列{Ui}，再进行均匀性和相关性检验； 通过检验后利用Box-Muller算法对其进行下列变换，生成一组服从标准正态分布的随机数序列{xi}，如式(1)所示。

(1)

式中：xi为生成的服从标准正态分布的随机数；Ui为服从均匀分布的随机数。

1.1.2 构造模拟观测值

隧道洞内平面控制网中包括了水平方向和水平距离2类观测值。为了得到水平方向与水平距离的设计值，首先要生成洞内所有平面控制点的设计坐标。生成设计坐标的方法有2种： 1)在洞内平面控制网完全未知的情况下，首先，自定义一个坐标系，一般以洞口一个控制点为坐标原点，以隧道(直线型)走向为X轴，垂直于隧道走向为Y轴； 然后，根据洞内控制点的纵向和横向间距生成各个控制点的设计坐标。2)在部分或全部的洞内控制网都已知的情况下，将实测数据处理后得到的各控制点原测坐标作为设计坐标； 然后，在设计坐标的基础上，通过坐标反算获取相邻控制点间水平距离与水平方向的设计值； 最后，按照式(2)添加服从正态分布且经过变换的伪随机数，即可得到水平距离与水平方向的模拟观测值。

(2)

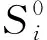
在洞内平面控制网未施测的情况下，可取测量用全站仪的标称精度； 若已经开始施测，则可取实测数据的验后精度。

1.2 仿真计算试验设计

基于1.1节的洞内平面控制网精度仿真计算原理，并结合新疆某特长引水隧洞洞内平面控制网的实际情况进行仿真计算试验设计。设计内容具体包括模拟洞内平面控制网的验前精度设计、测量网形设计和仿真计算试验方案的设计。

1.2.1 验前精度设计

本次仿真计算试验中，添加的随机观测误差包括测角中误差(可根据误差传播定律进一步转换为水平方向中误差)、测距中误差、洞口起算点的点位中误差。测角中误差取验前精度和验后精度2项，参照TB 10101—2018《铁路工程测量规范》[12]有关规定，验前精度取隧道二等测角精度(1.3″)，验后精度取该引水隧洞实测数据统计的测角精度(1.2″)； 水平距离测距中误差按照全站仪测距部分的标称精度1 mm+1 mm/km模拟； 洞口控制点(起算点)的点位中误差按照1 mm的精度模拟。

1.2.2 测量网形设计

为真实模拟洞内平面控制网的观测数据，仿真计算试验按照该引水隧洞洞内平面控制网的实际情况进行网形设计。模拟控制网中设置了3个洞口控制点，在长度为4 km左右的斜井段和长约18 km的正洞段均采用交叉导线网的布网方式，控制点间横向间距约为5 m，纵向间距约为300 m； 为了提升网形强度，在平面进洞联系测量位置加测1个自由测站的观测值，在斜井段加测3个自由测站的观测值，在斜井与正洞交叉口的平面联系测量位置加测5个自由测站的边角观测值，如图1所示。

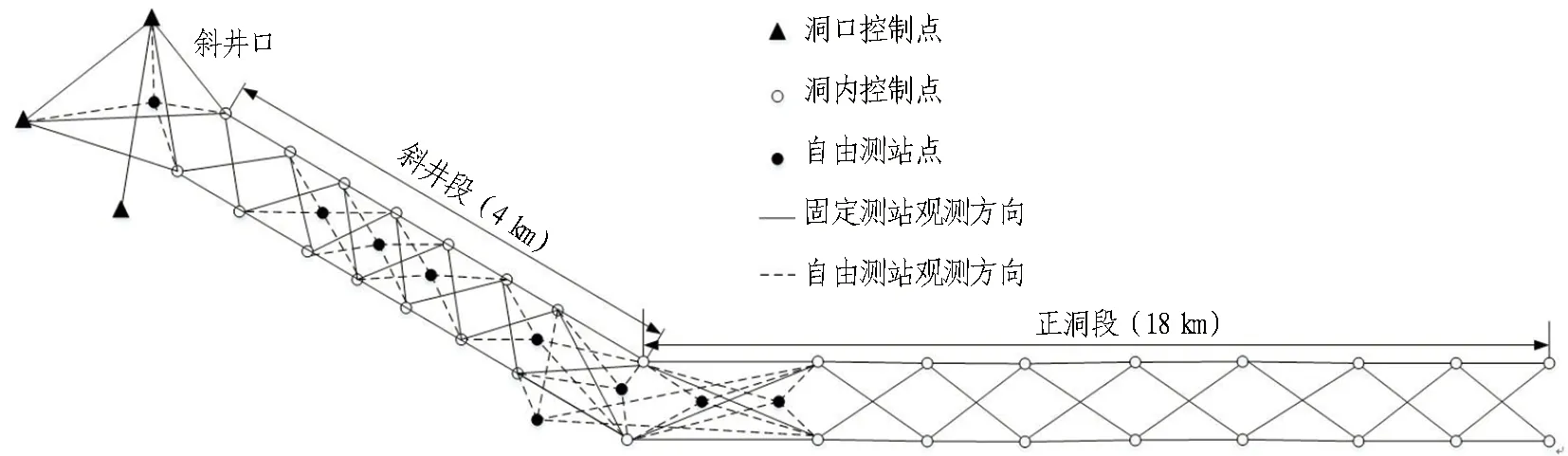
图1 仿真计算试验模拟的某引水隧洞洞内平面控制网网形Fig. 1 Plane control network of a water-diversion tunnel in simulation experiment

1.2.3 仿真计算试验方案设计

本次特长隧道洞内平面控制网精度仿真计算试验的实施步骤如下：

1)收集某引水隧洞洞内平面控制点及洞口控制点的往期坐标，将其作为隧道洞内平面控制网精度仿真计算的设计坐标，自由测站点坐标则根据其与平面控制点间的相对位置关系进行计算，如图1所示。

2)根据洞内平面控制点的往期坐标，反算出平面控制网中各个测站的水平方向及水平距离观测值的设计值[13]。

3)基于Box-Muller算法为各类观测值添加随机误差。添加的观测误差主要包括洞外进洞平面联系测量测站点的点位中误差、水平方向和水平距离观测误差。

4)将生成的点位中误差添加到平面联系测量测站点的设计坐标中，将模拟的水平方向和水平距离观测误差分别添加到洞内平面控制网中各个测站的水平方向与水平距离观测值的设计值中，从而得到洞内平面控制网中各个测站上的水平方向及水平距离仿真观测值。

5)根据上面得到的洞内平面控制网中的仿真观测值，按照常规定权方法，对该引水隧洞洞内平面控制网进行仿真平差计算，然后统计最弱点(即最靠近贯通面的一对控制点)的横向精度信息，并进一步计算该隧道的横向贯通中误差，计算方法如下。

假设贯通面处的一个控制点i在进洞方向的控制网中测量的坐标为(Xij,Yij)，出洞方向控制网中测量的坐标为(Xic,Yic)，则该隧道的横向贯通误差

ΔYi=Yij-Yic。

(3)

进洞方向的洞内平面控制网和出洞方向的洞内平面控制网在贯通时是各自独立施测的，因此Yij和Yic误差相互独立。根据式(3)和误差传播定律[14-15]可得到该隧道贯通时的横向贯通中误差

(4)

式中mΔYij和mΔYic分别为进洞方向和出洞方向的控制网中位于贯通面处的控制点的横向坐标中误差。

6)按照上述步骤重复进行50次独立仿真计算试验，然后统计50次仿真计算试验结果的横向贯通中误差的平均值、最大值及最小值。

1.3 仿真计算试验结果分析

按照上述仿真计算试验方案和模拟的某引水隧洞斜井及正洞段的洞内平面控制网观测数据，利用平差软件对50次独立仿真的洞内平面控制网进行平差处理。平差处理前对洞内控制点坐标进行旋转，使正洞段贯通面附近的洞内控制点的X坐标轴与隧道走向平行、Y坐标轴与贯通面平行，这样便可将平差后最弱点(即最靠近贯通面的一对控制点)Y坐标中误差按照式(4)计算，得到贯通面处的横向贯通中误差。

为研究仿真计算结果的离散性，统计50次独立仿真计算的横向贯通中误差的平均值、最大值、最小值和极差，结果见表1。

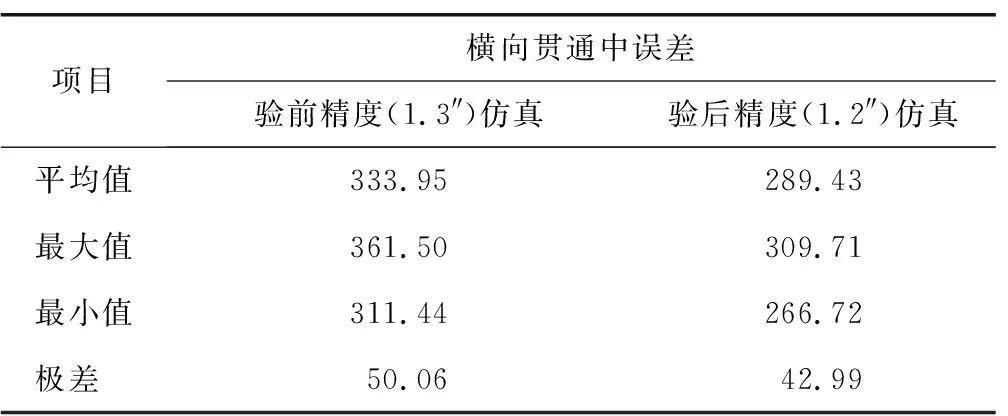
表1 50次仿真计算横向贯通中误差统计情况Table 1 Statistics of root mean square error of transverse penetration by 50 simulation calculations mm

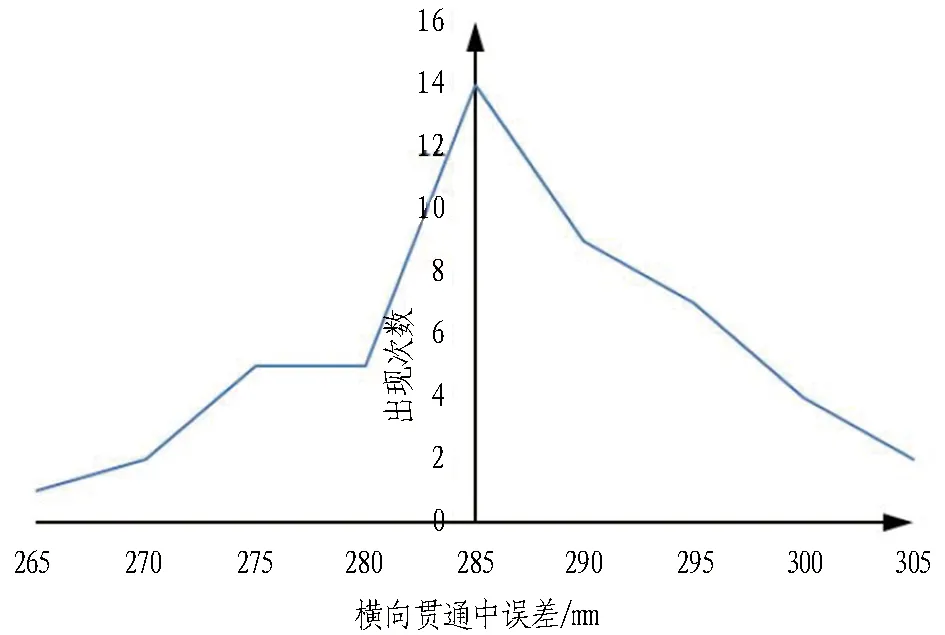
由表1可知，2种仿真精度条件下进行的50次独立仿真计算，得到的横向贯通中误差的极差均在5 cm左右，即波动范围约为5 cm，占平均值的14%～15%，说明多次仿真计算的结果较为稳定。根据中误差的特性，仿真计算的横向贯通中误差应符合正态分布规律[9]，为了验证50次仿真计算的次数是足够的，以每5 mm为1个区间，分别统计2种精度条件下仿真计算的横向贯通中误差在各个区间内的出现次数，统计结果如图2所示。

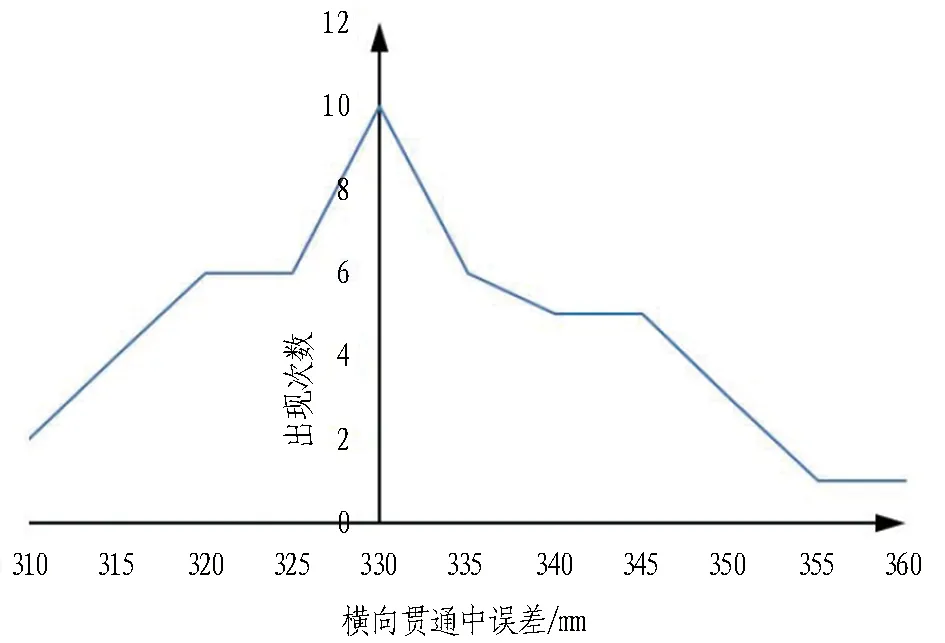
(a) 验前精度(1.3″)

(b) 验后精度(1.2″)图2 2种精度仿真计算的横向贯通中误差的区间分布Fig. 2 Interval distribution of root mean square error of transverse penetration calculated by two kinds of precision simulation

由图2可知： 2条曲线的高峰大致在中央位置，即均值所在的位置； 曲线以均值为中心，左右侧近似对称； 曲线由均值所在处开始分别向左右两侧逐渐下降。曲线的以上特征均与正态分布的概率密度函数曲线类似，说明50次仿真计算的横向贯通中误差趋于服从正态分布。

本次仿真计算试验最后取50次仿真结果的平均值作为最终横向贯通中误差预计值。由表1可知，该引水隧洞相向开挖长度(含支洞长度)约45 km的隧道横向贯通中误差预计值分别为333.95 mm(验前精度1.3″)和289.43 mm(验后精度1.2″)，均满足SL 52—2015《水利水电工程施工测量规范》[16]中规定的贯通距离为40～45 km洞内控制网测量误差引起的横向贯通中误差440 mm的限差要求。

2 模拟网形的工程应用及其实测结果分析

2.1 工程概况及施测方法

某特长引水隧洞地处新疆准噶尔盆地东北部，工程穿越阿尔泰山南坡和东天山北坡之间的低山区、丘陵区，全长约为283.39 km，是目前在建的世界最长输水隧洞[6]。其中，某标段工程主要包括长约19.87 km的正洞及一段长约4 km的斜井，斜井与正洞的交叉口向小里程方向为钻爆法开挖洞段，向大里程方向则为TBM开挖洞段，如图3所示。

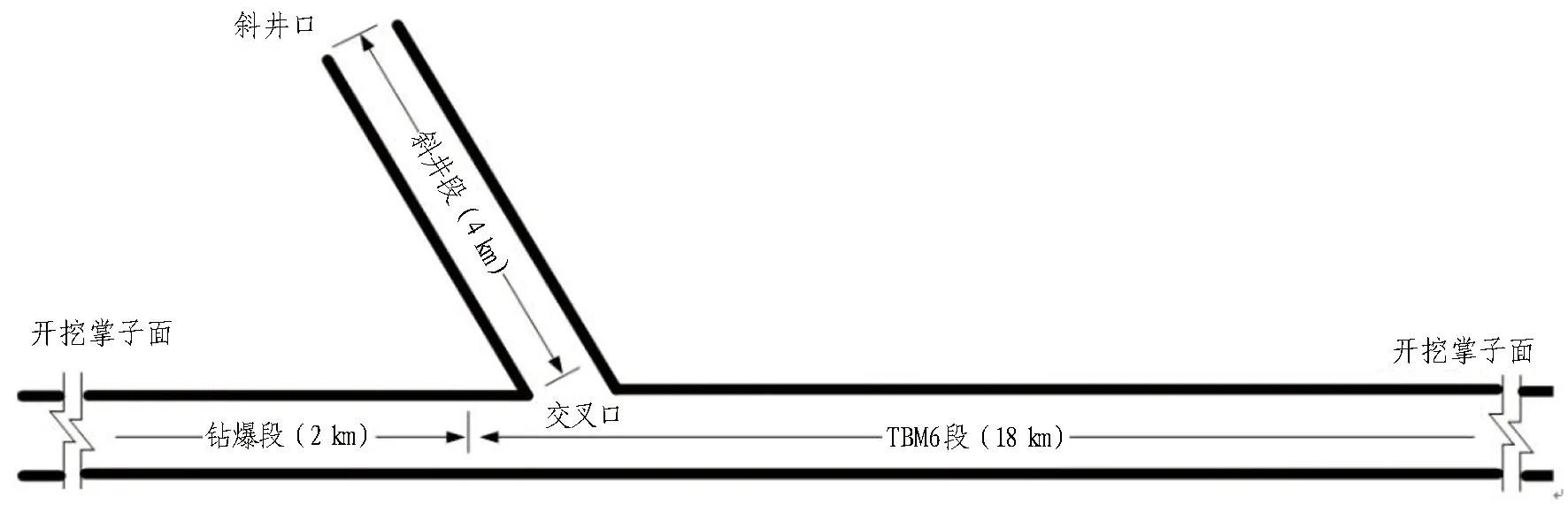
图3 某特长引水隧洞某标段洞内工程示意图Fig. 3 Sketch of in-hole project in a section of a super-long water-diversion tunnel

本次布网施测的隧道段落主要为一段4 km左右的斜井和18 km左右TBM开挖的正洞段落。在原洞内交叉导线网的基础上，按照如图1所示的仿真模拟网形进行布网及施测。根据现场实际情况，在斜井的第3至第6对控制点之间和横洞与正洞交叉口处分别加测3个及5个自由测站的边角观测值。

2.2 实测数据分析

根据上述测量网形及测量方法，参照TB 10101—2018《铁路工程测量规范》有关规定，按照导线测量中隧道二等的外业观测要求进行洞内平面控制测量，得到该引水隧洞洞内21 km左右的平面控制网实测数据。在网平差处理前，对观测的水平距离与水平角的验前精度指标进行统计和分析。

首先，对平面网测量的水平距离验前精度进行计算和分析，结果见表2。由表2中的信息可知，每km测距中误差仅为0.70 mm，导线边最大测距中误差不超过2 mm，均满足隧道二等的精度要求； 另外，各导线边往返测距离较差。达到隧道二等要求的占比为99.3%，总体而言本次观测的水平距离测距精度较高。然后，对实测水平角的验前精度进行统计分析，结果见表3。

表2 实测水平距离验前精度统计表Table 2 Statistics of precision of measured horizontal distance before adjustment

表3 实测水平角验前精度统计表Table 3 Statistics of accuracy of measured horizontal angle before adjustment

由表3可知，该引水隧洞洞内平面控制测量共形成142个四边形闭合环，角度闭合差最大值为5.3″，合格率达96%以上。水平角测角中误差为1.20″，达到了隧道二等平面控制网的测角精度要求。

2.3 隧道横向贯通中误差预计

由于该引水隧洞采用独头掘进的方式进行开挖，独头掘进距离已超过20 km，为预测隧道能否顺利贯通，需要对隧道横向贯通误差进行预计。为此，还需要先将隧道工程独立坐标系的起算点坐标进行转换，使得旋转后的坐标系以贯通面附近隧道中线为X轴、以隧道中线垂直方向为Y轴，以转换后的起算点坐标为起算数据进行约束平差，从而得到最靠近贯通面的洞内控制点在纵横向坐标系中的坐标及其中误差，见表4。

表4 贯通点坐标及其点位精度Table 4 Coordinates of penetration point and its precision

表4中的平差结果显示，该段平面控制网在最靠近贯通面处控制点的点位横向坐标中误差为223.73 mm，假设与该段隧道相向施工并进行贯通的另一段隧道洞内平面控制网的精度与表4中的精度基本相当，则按照式(4)可估算出该45 km左右特长引水隧洞的横向贯通中误差值约为316.35 mm，能够满足SL 52—2015《水力水电工程施工测量规范》[16]中规定的贯通距离为40～45 km洞内控制网测量误差引起的横向贯通中误差440 mm的限差要求。

3 仿真计算结果与实测结果的对比分析

2.3节已根据该引水隧洞洞内平面控制网实测数据估算出隧道横向贯通中误差，1.3节也分别在2种不同精度条件下通过50次独立仿真计算得到横向贯通中误差预计值，据此可以绘制出实测数据与仿真数据估算的横向贯通中误差分布图，如图4所示。由图4可知，由实测数据估算的横向贯通中误差介于验后精度(1.2″)仿真计算的横向贯通中误差与验前精度(1.3″)仿真计算的横向贯通中误差之间，并且与验前精度更为接近。

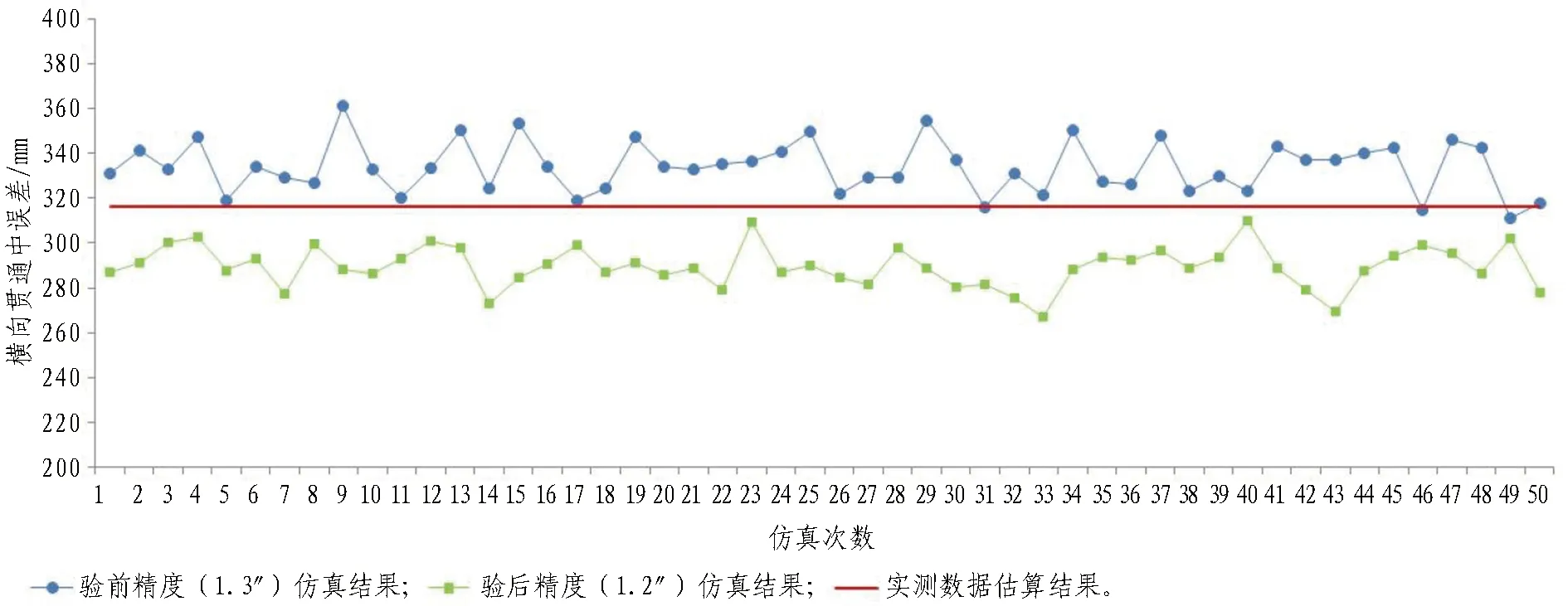
图4 仿真计算与实测数据估算的横向贯通中误差分布图Fig. 4 Distribution of root mean square error of transverse penetration by simulation and measured data

对50次仿真结果取均值后与实测数据估算结果进行对比，结果见表5。由表5可知，按照验前精度仿真计算得到的横向贯通中误差比实测数据估算的横向贯通中误差要大17.55 mm，该偏差仅为实测结果的5.5%； 按照验后精度仿真计算得到的横向贯通中误差比实测数据估算的横向贯通中误差要小26.97 mm，该偏差约为实测结果的8.5%。由此可以说明，在给定合适的仿真精度及模拟实际洞内平面控制测量网形的基础上，采用本文的方法进行隧道洞内平面控制网的精度仿真计算，能够较为准确地模拟出与实测数据相当接近的平面控制网观测数据及其横向贯通中误差。

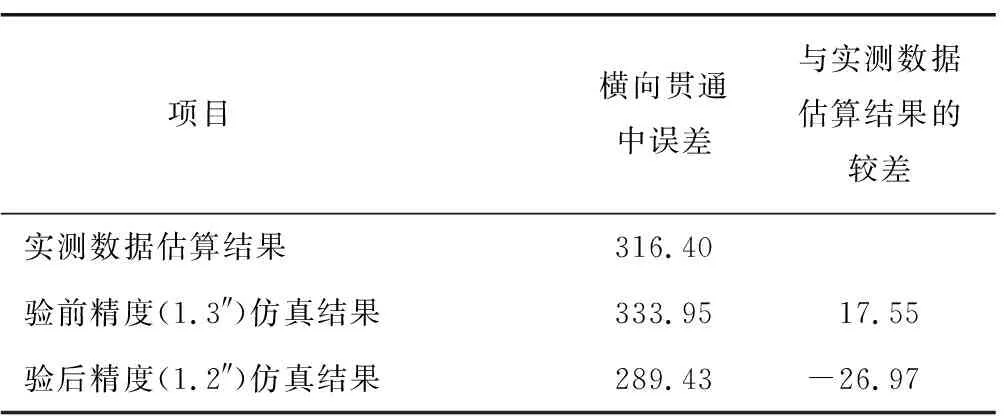
表5 仿真计算结果(均值)与实测数据估算结果的较差Table 5 Difference between simulation results(mean value) and estimation results from measured data mm

4 结论与讨论

通过本文的特长隧道洞内平面控制网精度的仿真计算试验及与某特长引水隧洞洞内平面控制测量实测数据的对比分析，可以得到以下主要结论：

1)特长引水隧洞在采用固定测站和自由测站相结合的构网方式进行进洞处和斜井与主洞交汇处的平面联系测量，能够有效地提升洞内关键地段平面控制网的图形强度，并提高最终的横向贯通精度。

2)通过将特长隧道洞内平面控制网横向贯通精度的仿真计算结果与实测数据估算结果进行对比分析，表明了在给定合适的验前精度及模拟洞内平面控制网实际测量网形的基础上，本文的仿真计算方法用于估算特长引水隧洞横向贯通精度具有一定的准确性和可靠性。

3)特长隧道洞内平面控制网施测前，应先在施测方案设计时采用本文的方法进行精度的仿真计算分析，必要时对施测方案进行调整，仿真计算结果通过后再按照仿真计算的网形和精度等级进行施测，这样就可确保洞内平面控制网施测结果满足特长隧道横向贯通精度的要求。

采用本文基于实测精度和实际隧道洞内网形的仿真计算方法估算隧道洞内横向贯通中误差时，考虑到的观测误差包括测角、测距及洞外点位误差，但在实际测量中，还存在隧道洞内双侧壁水平旁折光对水平角测量产生的误差影响，且不可忽略。因此，旁折光对于水平角观测值的影响规律及如何在仿真计算中加入此项误差将是未来的研究方向之一。