坝面钢筋网内混凝土振捣机器人轨迹规划

李 檬，李成刚，钱鸿巍，储亚东

(南京航空航天大学机电学院，江苏 南京 210016)

0 引言

随着工业4.0的到来，越来越多的领域用到机器人。特殊用途的机器人发展也很迅猛，包括军事、航天、水下搜救以及医疗等[1]。近年来，我国大坝建设已步入加速发展阶段，大坝工程的建设理念由传统人为主导模式向数字化、智能化模式转变。“智能振捣”成为新一代混凝土平仓振捣机的发展目标，也是应对未来水利水电行业特高拱坝建设的需要[2]。本文设计了一款五自由度串联智能振捣机器人，体积小，工作灵活，能代替人工手持振捣棒方式，高效、高质量地完成钢筋网内混凝土的振捣施工作业。

1 振捣机器人运动学建模

1.1 振捣机器人模型

振捣机器人模型如图1所示。该机器人具有5个旋转自由度，平面内为三连杆串联，分为大臂、小臂和末端臂，固定座底部装有摆动缸带动整体旋转，末端臂上装有旋转马达带动振捣棒旋转，整体构成五自由度串联机器人。

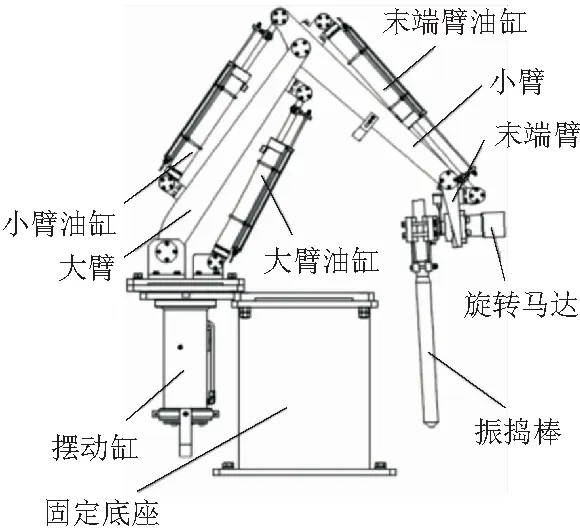
图1 振捣机器人模型

1.2 运动学空间的划分

按照变量选取的不同，将运动学模型划分为4个工作空间，分别为位姿空间、关节空间、驱动空间和反馈空间。位姿空间主要由机器人末端执行器的位置(x,y,z)与姿态角(β,α)组成；关节空间主要由大臂、小臂和末端臂的关节角度θ2、θ3、θ4和摆动缸、振捣棒的转角θ1、θ5组成；驱动空间主要由机器人各关节液压油缸长度变量q1、q2、q3组成；反馈空间主要由位移传感器的反馈信号决定，与驱动空间存在一定的差值，是实现闭环位置控制的基础。振捣机器人工作空间转化关系如图2所示。

图2 振捣机器人各工作空间映射关系

1.3 振捣机器人正运动学

对振捣机器人建立连杆坐标系如图3所示，图中所示方向为各角度正方向。

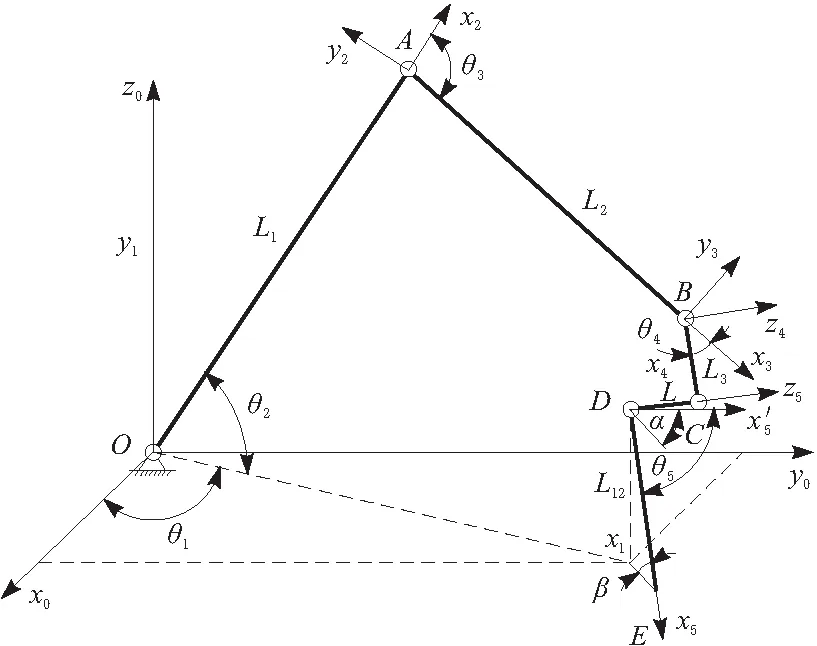
图3 机器人连杆坐标系

基于机器人D-H方法[3]，计算各连杆坐标系的齐次变换矩阵，可得到执行器末端的位姿[4]，即

(1)

[nxnynz]T、[oxoyoz]T、[axayaz]T为机器人末端坐标系相对于基座坐标系的旋转向量，即：

(2)

(3)

(4)

[pxpypz]T为机器人执行器末端坐标系相对于机器人基座坐标系的位置，即

(5)

1.4 振捣机器人逆运动学

机器人逆运动学是指已知机器人执行器末端位姿，即已知齐次变换矩阵0T5，求解各转动关节角度θi[5]。为了更直观对机器人关节变量进行求解,采用几何法[6-8]，机器人关节角几何约束如图3所示。

设振捣棒末端点D的坐标为(xD,yD,zD)，β为振捣棒与xoy正方向的夹角，α为振捣棒与yoz正方向的夹角。由此可得振捣棒末端点E的坐标为

(6)

根据振捣棒末端点D的坐标，可得

θ1=arctan(xD/yD)

(7)

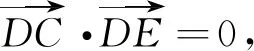
(8)

其中，XCD=xC-xD,XED=xE-xD,YED=yE-yD，ZED=zE-zD,k=yD/zD。

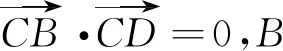
(9)

其中，XBC=xB-xC,XDC=xD-xC,YDC=yD-yC,ZDC=zD-zC,k1=yC/zC。

根据机械臂几何关系可得

(10)

面ODC与面CDE的夹角为θ5,设面ODC的平面方程为A1x+B1y+C1z=0,面CDE的平面方程为A2x+B2y+C2z+D=0，则

(11)

其中

(12)

鉴于振捣机器人的大臂、小臂和末端臂驱动部件是液压油缸如图4所示，因此，逆运动学求解的最终目的是得到执行器末端位姿与驱动空间的直线位移之间的映射关系[9]。

图4 机器人驱动空间几何关系

根据机器人的几何参数，如表1所示，结合油缸和连杆之间的几何关系，利用余弦定理可求解出各连杆所对应的关节角度变量θ2、θ3、θ4与油缸驱动变量q1、q2、q3之间的映射方程，即

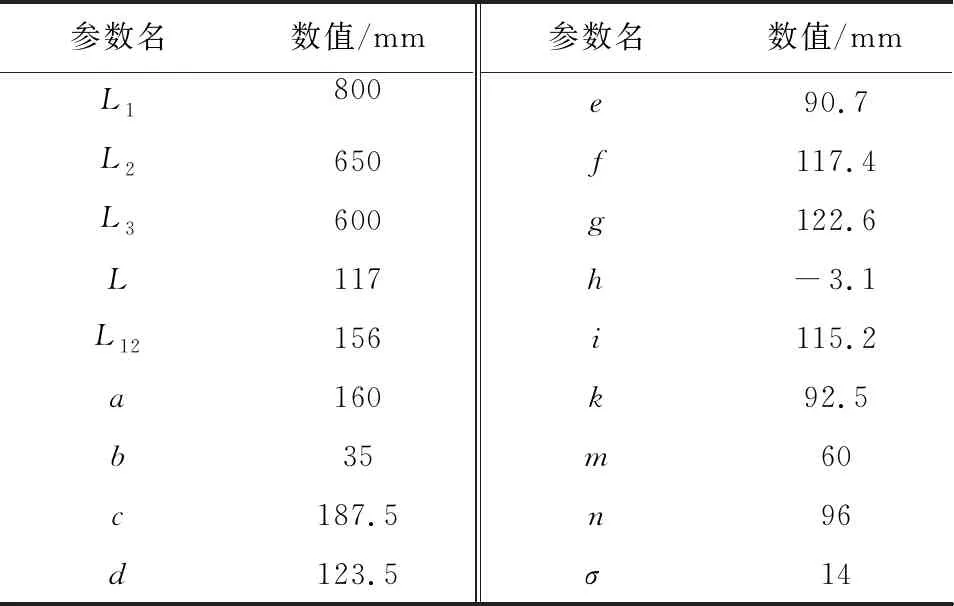
表1 机器人几何参数

(13)

1.5 逆运动学解的分析

机器人执行器末端到达某一位置时，机器人的姿态并不是唯一的，逆运动学存在多解的情况。在同时考虑关节范围和工况要求的情况下，存在的逆解和可用的逆解需要根据实际的机器人进行进一步分析。几何关系以及计算过程如表2所示。

表2 逆解情况分析

最终求得2组可用逆解。通过对其分析，为后面轨迹规划和运动控制策略做了铺垫，在该机器人的轨迹规划中，轨迹上相邻的2个插值点，对应的逆解应该选择变化较小的解作为最优解[10-12]。

2 基于正弦加减速的机器人轨迹规划

传统的梯形加减速等轨迹规划算法存在启停过程加速度不平稳等问题，容易造成机器人的冲击与振动[13]。本文引入改进的正弦加减速算法，对机器人执行器的位置(x,y,z)和倾角(β,α)进行轨迹规划，保证执行器启停阶段能平稳运行。

设机器人末端执行器从Mo点沿直线运动到Mm点，起始点Mo位姿为(xo,yo,zo,βo,αo)，终点Mm位姿为(xm,ym,zm,βm,αm)，采用插补的方法[14]，插补周期为t，从起点到第i个插补点的直线位移为sL(t)，角位移是sθ(t)。将直线MoMm表示为关于时间t的方程形式，第i个插补点的位姿分别为

(14)

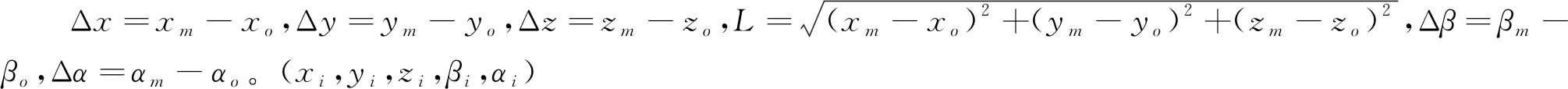
本文设计的正弦加减速轨迹规划将直线阶段分为3段，如图5所示。

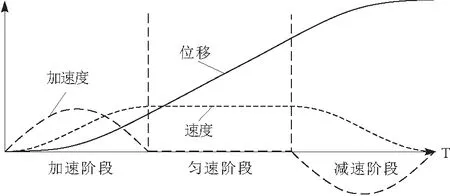
图5 正弦加减速轨迹规划

a.加速阶段：加速度a随时间按正弦规律变化，从0变化到最大值，再变化为0。速度在此阶段也会从0达到最大值，即匀速阶段速度Vm。

b.匀速阶段：以恒定速度Vm运行至减速阶段。

c.减速阶段：加速度随时间按正弦规律变化，从0变化到最小值，再变化为0。速度在此阶段也会从匀速阶段速度Vm减小到0，此时机器人末端执行器走完预设轨迹，到达目标振捣点，运行结束。

给定若干个插补点，设匀速段速度Vm、角速度wm、最大加速度amax、最大角加速度εmax，整个过程的加速度表达式为

(15)

速度表达式为

(16)

位移表达式为

si(t)=

(17)

当规划直线段位移si(t)时，A=amax；当规划执行器末端倾角sθ(t)时，A=εmax。

各参数确定好之后，需校验是否存在匀速段速度，即在给定加速度的情况下，末端执行器可以经历加速、匀速和减速3段完整运动的过程。设末端执行器加速到最大速度后直接进入减速阶段，则t1=T-t1=t2，加速段位移为

(18)

综上，振捣机器人总位姿变量(xi,yi,zi,βi,αi)已求出，下文进行实验验证。

3 实物调试验证

振捣机器人实物样机如图6所示。平面为三自由度机械臂串联结构，机械臂上方布置了油缸，油缸上方安装了位移传感器，传感器的测量端子与活塞杆同步运动。固定座底部装有摆动缸，带动机器人整体旋转，摆动缸转角由角位移传感器可得。末端臂上装有旋转马达，带动振捣棒旋转，振捣棒旋转角度由安装在法兰盘上的拉线位移传感器可得。

图6 振捣机器人实物样机

在振捣机器人上对设计的正弦加减速算法进行验证，给定末端执行器初始位置和终点位置，经插补运动，最终得到3个油缸实际的跟踪轨迹，如图7所示。

图7 油缸跟踪轨迹

由图7可知，机械臂油缸的实际位移与期望位移基本一致。在运动过程中大臂和小臂的液压油缸是逐渐缩回状态，而末端臂是逐渐伸长状态，走同一个正弦加减速轨迹，根据设定的最大加速度值不同，曲线的峰值略有不同，但总体运动趋势与图5规划的位移轨迹相符，有完整的加速、匀速和减速3段运动，运动平稳，没有突变。大臂和小臂存在较小延迟，符合预期情况。改进的正弦加减速算法能从起点平稳的运行到终点，在一定程度上延长了机器人的使用寿命[15]。

4 结束语

本文通过D-H法建立了五自由度振捣机器人的坐标系，采用几何法推导了机器人的运动学模型，将关节空间变量映射到驱动空间，采用改进的正弦加减速方法规划了末端执行器在笛卡尔空间的轨迹，使其在运动阶段平滑过渡，无冲击，并进行了实验验证。通过实验反映出机器人运动的实际情况，验证了轨迹规划的正确性以及合理性。