OSPF协议中Dijkstra算法的仿真实现

2023-02-28 12:24:53谢光艺

现代信息科技 2023年20期

摘要：OSPF协议是计算机网络常用的路由协议，它采用了Dijkstra算法。Dijkstra算法在各领域都有广泛的应用，掌握其原理很有必要，因此提出在MATLAB中利用三重循环实现算法的仿真。首先确定代价矩阵，明确起始路由器，并把该路由器放入到S集中。其次采用最外层循环判断是否遍历全部路由器，中间循环遍历S集中的路由器，里层循环遍历U集中的路由器，寻找到每一次外层循环时距起始路由器的代价最小的路由器，并把这个路由器移出U集，并放入到S集中。最后通过回溯方法得到最短路径树。通过仿真实验，不仅能帮助掌握OSPF协议中路由的选择方法，更能加深对Dijkstra算法的理解。

关键词：OSPF协议；Dijkstra算法；三重循环仿真

中图分类号：TP393.0；TP301 文献标识码：A 文章编号：2096-4706（2023）20-0096-04

Simulation Implementation of Dijkstra's Algorithm in OSPF Protocol

XIE Guangyi

（Intelligent Science and Information Engineering College， Xi'an Peihua University， Xi'an 710125， China）

Abstract： OSPF protocol is a commonly used routing protocol in computer network， and it adopts Dijkstra's Algorithm. The Dijkstra's Algorithm has a wide range of applications in various fields， and it is necessary to master its principle. Therefore， using the triple-loop to realize algorithm simulation is proposed in MATLAB. Firstly， this paper determines the cost matrix， identifies the starting router， and puts the router into the S set. Secondly， the outermost loop is used to determine whether to traverse all the routers， the middle loop traverses the routers in the S set， and the inner loop traverses the routers in the U set to find the router with the smallest cost from the starting router in each outer loop. It moves this router out of the U set and puts it into the S set. Finally， the shortest path tree can be obtained by the backtracking method. The simulation experiments can not only help master the route selection method in OSPF protocol， but also deepen the understanding of Dijkstra's Algorithm.

Keywords： OSPF protocol; Dijkstra's Algorithm; triple-loop simulation

0 引言

路由协议作为TCP/IP协议族中重要的组成部分，其决定信息交换双方网络路径的选择，从而会对Internet网络的整体效率产生影响[1-4]。内部网关路由协议主要有：RIP，IS-IS和OSPF。RIP路由协议是基于距离向量（DV）算法，它通过和相邻路由器交换信息更新路由表。RIP路由协议适用于小的网络，它具有方便配置和管理的优点，但它的最大跳数为15跳，当有多个网络时会出现环路，并且存在“好消息传得快，坏消息传得慢”等问题。因此大型网络通常采用基于链路状态（LS）的IS-IS和OSPF算法。

OSPF协议属于链路状态路由協议，它为“开放式最短路径优先（Open Shortest Path First）”的缩写形式。每台OSPF路由器都会生成相关的LSA（Link-State Advertisement），并将这些LSA广播出去。路由器收到LSA后，会将它们存放在链路状态数据库，再利用最短路径优先SPF（Short Path First）算法得到网络路由表。由于OSPF路由协议具有开放、收敛速度较快和良好的扩展性，所以OSPF协议在各种计算机网络中得到广泛应用。当然与其他的最短路径优先协议一样，OSPF协议也基于Dijkstra算法，这个算法与基于距离向量的最短路径算法不同，它会考虑到网络的链路状态以及负载。

Dijkstra经典和改进算法在配电网络、雷达目标识别、航摄影像拼接和道路航规划等领域有广泛的应用。文献[6]针对飞行器在航行途中遇到突发情况需要临时更改路径时，提出了一种加入预搜索的Dijkstra算法改进方案。文献[7]提出了利用Dijkstra算法改进遗传算法进行定向越野赛道设计的方法，实现军事定向越野多目标多路径规划从而自动获取最优路线。文献[8]提出一种基于Dijkstra算法的分簇路由，利用Dijkstra算法构建簇头间的最短路径，进而减少簇头消耗的能量，有利于无线传感网络寿命的延长。文献[9]提出基于改进的Dijkstra算法结合时频域滤波实现雷达目标识别算法。该方法利用改进的Dijkstra算法提取雷达回波信息中最大分量的瞬时多普勒特征，从而提高雷达识别弹道中段目标的准确率。文献[10]利用优化的Dijkstra算法在航空图重叠区域找出错位差异最小的路径作为航摄影像镶嵌线，最终拼接多幅航摄影像形成实用的可视化产品和决策工具。

MATLAB软件是常用的科学计算和仿真软件，通过使用它来模拟Dijkstra算法，不仅能帮学生掌握OSPF协议[11-13]中路由的选择方法，更能加深学生对Dijkstra算法的理解，达到举一反三的效果。

1 Dijkstra算法原理

1.1 Dijkstra算法

Dijkstra算法采用贪心算法思想，即不断贪心的选取当前最优策略的计算方法。首先计算出当前节点到所有可达节点间的代價，并找出最小代价，然后松弛一次继续循环。所谓松弛一次，就是在已访问过的节点中遍历一次，看看有没有代价更小的，如果有更小的就更新代价值。这样每次找出代价最小的可达节点，并结合松弛遍历历史节点的操作，能存下起始节点到其他所有节点的最小代价，最终找到代价最小的最优路径。

1.2 Dijkstra程序步骤

1）起始时，S集只包含起始节点s；U集中包含除s外的其他所有节点，且U中节点的代价为“起始节点s到该节点的代价”（例如U中节点v的代价表示为（s，v），如果s和v不相邻，则v的代价为∞）。

2）从U中选出“代价最短的节点w”，并将节点w加入S中；同时从U中移除节点w。

3）更新U中各个节点到起始节点s的代价。之所以更新U中节点的代价，是由于上一步中确定了w是求出小代价的节点，从而可以利用w来更新其他节点的代价；例如已有（s，v）的代价可能大于（s，w）+（k，w）的代价。

4）重复步骤2）、3），直到U集为空。

2 Dijkstra算法实现

以图1所示的一个局部网络为例，其中有7台路由器，分别为路由器R1、R2、…、R7，线上所标注为相邻路由器之间的代价，即权值，求R1到其他各路由器的最短距离（即最小代价）。

2.1 定义变量

路由器个数n；

矩阵S （1×n）对应S集中的路由器，若第i个路由器已找到最短路径，则S（i） = 1，否则等于0，对于初始路由器，S = 1；

矩阵d （1×n）存储最小代价，假如第i个路由器已找到最短路径，则d （i） = 最小代价，否则为0，初始路由器d = 0；

矩阵PreviousRouter表示找到最短路径时的上一路由器，记为PR （1×n）。若第i个路由器找到了最短路径，则PR存放这一条最短路径的前一个路由器，通过对每一个路由器的回溯，可以找到最短路径。

2.2 初始代价矩阵

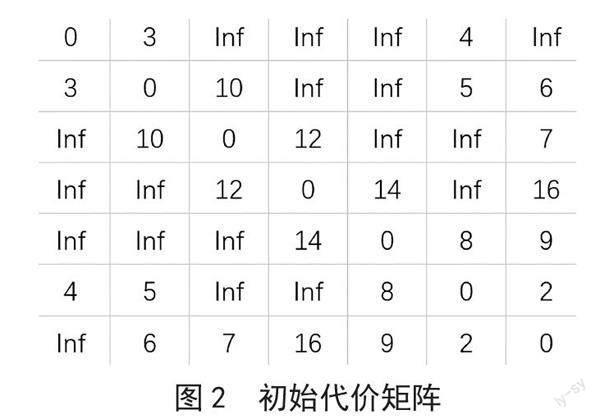
二维矩阵M （n×n）存放路由器间的初始代价。相邻的路由器间代价为有限值，不直接相连的路由器间代价为正无穷，路由器自身的代价为0，按照这个标准得到图1中各路由器间的代价，如图2所示。

2.3 算法过程

确定初始路由器为R1，则Rf （1） = 1。在与R1连通的路由器中（在矩阵M的第1行）寻找最小值，最小值所在列即是最小代价的路由器。如M中所示第二列即R2值最小，d（2） = 3，S（2） = 1，对于已找到最小代价的路由器R2的上一路由器为R1，PR（2） = 1。下一步，计算与R1连通且未找到最小代价的路由器的代价，并与通过R2连通R1的代价进行比较，通过以上两种路径寻找最小代价，如图M中最小为R6，即得到d（6） = 4，S（6） = 1，PR（6） = 1。

重复以上步骤可以发现，每次所要寻找的最小代价路由器x （x ∈ U），要通过已找到最小代价的路由器w （w ∈ S）与它相邻的未找到最小代价的路由器v （v ∈ U）间的运算来得到。要将两个路由器之间代价与路由器w到初始路由器的代价值相加，比路由器v到初始路由器的代价值小则更新，否则不变。遍历一次并找到其中代价值最小的路由器，即为所需路由器x，并从U集中移除、加入S集中，然后开始新的循环。

2.4 算法伪代码

算法伪代码如下所示：

函数 Dijkstra（Graph， source）：

create vertex set U

for each vertex v in Graph： // 初始化

d [v] ← INFINITY // Unknown distance from source to v

PR [v] ← UNDEFINED // Previous node in optimal path from source

add v to U // All nodes initially in U （unvisited nodes）

d[source] ← 0 // Distance from source to source

add source to S

remove source from U

while U is not empty：

for each v of U：

for each vertex u of S

alt ← d[u] + length（u， v）

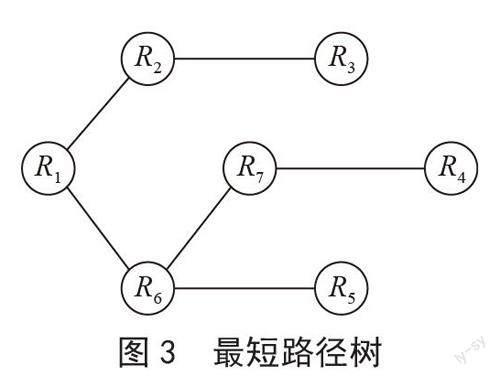
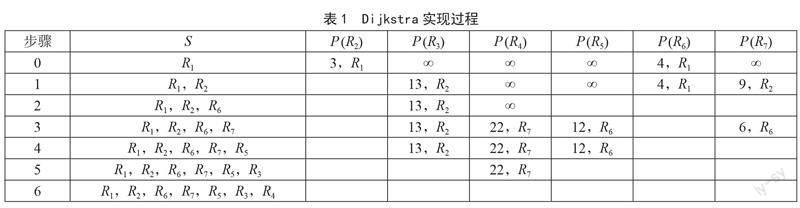
if alt

d[v] ← alt

PR[v] ←u

d（w）=min（d（v）） //v in U

add w to S

remove w from U

return d []， PR []

特別说明，在MATLAB软件中利用find（S==0）命令即可找到U集中的路由器，而利用find（S==1）命令即可找到S集中的路由器。找到最小代价的路由器时只要把S集中的相应位置置1，即可表示把该路由器从U集中移到S集中，这样更能体现MATLAB编程中利用find命令的优越性。

3 实验结果

表1列出了理论分析图，其中P（Ri） = （di，PR（i）），表示路由器Ri至路由器R1的代价为和di，上一级连接的路由器为PR（i）。指定路由器R1为初始路由器，和R1直接相连的有R2和R6路由器，它们到R1的代价分别为3和4，3小于4，所以下一步把R2路由器选中并放入到S集中，通过R2分别计算相邻路由器R3、R6、R7到R1的代价，如果小于原先的代价就更新，并找出最小代价的路由器，此时是R6。然后重复此步骤，最终得到算法的实现过程如表1所示。

从实验结果来看，从R1出发，依次找到最小代价路由器R2、R6、R7、R5、R3，最后为R4，和理论分析是一致的。通过跟踪前继路由器构建最短路径树，如图3所示。

算法的复杂度分析如下：具有n+1个路由器的计算机网络，对于指定起始路由器的Dijkstra算法而言，执行三个嵌套的循环最耗费时间，外层循环需要n次，复杂度为O（n）；后两层循环共计执行n次，每次复杂度为O（n），因此总的时间复杂度为O（n2）。对于从任意路由器出发的情况，也就是以每个路由器作为起始路由器，需要执行n次Dijkstra算法，所以总的时间复杂度为O（n3）。

4 结论

OSPF协议是计算机网络常用的路由协议，采用Packet Tracer等软件仿真OSPF协议的实际应用较多，探索内部原理的较少，我们要做到“知其然”，更要“知其所以然”。为了实现OSPF协议所采用的Dijkstra算法的仿真，要首先确定初始代价矩阵，明确起始路由器，不断地把U集中到起始路由器最小代价的路由器移到S集中，再依据这个新加入的路由器以一定规则更新U集中和它相邻路由器的代价和，找到最小的代价，并把此路由器再移到S集中，这样循环直到U集中为空，最后利用回溯方法得到最短路径树。理论分析和实验结果表明所提方法能够在MATLAB软件中动态显示Dijkstra算法的过程，从而帮助学习者更好的理解掌握Dijkstra算法原理，为设计更优的计算机网络打下厚实的基础。

参考文献：

[1] 易典，刘渊，王晓锋.基于虚拟化的OSPF协议安全性仿真评估方法 [J].小型微型计算机系统，2023，44（5）：1052-1060.

[2] 郭文普，陈天豪，杨百龙.基于eNSP的中小型企业组网实验设计 [J].实验室研究与探索，2022，41（2）：125-129+296.

[3] 邱鹏，霍瑛，蒋悦.基于H3C Cloud Lab的企业网络设计与仿真 [J].实验室研究与探索，2020，39（10）：118-125.

[4] 李永芳.一种跨域铁路数据网综合组网设计与仿真 [J].实验室研究与探索，2021，40（2）：102-108+126.

[5] 李彦刚，邓文平，王宏，等.域内路由协议OSPF与IS-IS差异性的研究与分析 [J].计算机科学，2015，42（S1）：256-259.

[6] 郑弈，谢亚琴.基于Dijkstra算法改进的飞行器航迹快速规划算法 [J].电子测量技术，2022，45（12）：73-79.

[7] 欧丽珍，杨旭，李新梦，等.基于Dijkstra改进遗传算法的定向越野赛道设计 [J].火力与指挥控制，2022，47（4）：29-33.

[8] 张慧娟.无线传感网络中基于Dijkstra算法的分簇路由 [J].火力与指挥控制，2022，47（2）：134-139+145.

[9] 王彩云，姚晨，吴钇达，等.基于改进Dijkstra算法与时频域滤波的雷达目标识别 [J].系统工程与电子技术，2022，44（10）：3090-3095.

[10] 刘瀚阳，王博帅，王凤艳，等.一种基于重叠区指数化互相关和优化Dijkstra算法的航摄影像镶嵌线选取方法 [J].吉林大学学报：地球科学版，2022，52（2）：662-668.

[11] 赵婧如.基于Packet Tracer的多区域OSPF仿真实验设计 [J].现代信息科技，2021，5（14）：113-115+120.