一种改进惯性权重的粒子群优化算法

摘  要：针对粒子群算法易陷入局部最优解的问题，提出一种改进惯性权重的粒子群优化算法（CWPSO）。首先引入Sigmoid函数构造自适应的惯性权重策略；然后引入线性递减的惯性权重策略；最后通过群体适应度方差将自适应惯性权重策略和线性递减惯性权重策略动态结合，构造综合惯性权重策略，以提高算法全局搜索和局部搜索的能力。实验结果表明，CWPSO算法的寻优性能相较于对比算法有明显提升。

关键词：粒子群算法；惯性权重；适应值；群体适应度方差

中图分类号：TP18  文献标识码：A  文章编号：2096-4706（2023）20-0088-04

Particle Swarm Optimization Algorithm with Improved Inertia Weight

XUE Wen

（School of Electrical Engineering， Jilin Railway Technology College， Jilin  132299， China）

Abstract： Aiming at the problem that Particle Swarm Optimization is easy to fall into the local optimal solution， a CWPSO algorithm with improved inertia weight is proposed. Firstly， Sigmoid function is introduced to construct adaptive inertia weight strategy. Then the inertia weight strategy of linear decreasing is introduced. Finally， the adaptive inertia weight strategy and linear decreasing inertia weight strategy are dynamically combined by the variance of group fitness to construct a comprehensive inertia weight strategy， so as to improve the global search and local search ability of the algorithm. The experimental results show that the optimization performance of CWPSO algorithm is obviously improved compared with the comparison algorithm.

Keywords： Particle Swarm Optimization; inertia weight; adaptive value; variance of group fitness

0  引  言

粒子群算法（particle swarm optimization， PSO）是一种基于群体智能的随机全局优化算法，其具有实现简单、控制参数少等优点[1]，被广泛应用于工业工程领域[2-4]。但是，标准粒子群算法存在种群多样性损失过快导致算法早熟问题。

为了解决上述问题，近年来学者们对PSO算法提出了许多改进思路，改进思路主要分为以下三种：一是算法本身寻优公式的优化设计[5]；二是在算法寻优过程中加入辅助操作改进算法性能[6]；三是与其他算法相融合[7]。

受前人研究的启发，为了提升PSO算法的寻优能力，本文提出一种改进惯性权重的粒子群优化算法（CWPSO）。算法主要对标准PSO算法的惯性权重做作了3方面改进策略：一是利用S型函数非线性递增特性，构造基于适应值的自适应惯性权重更新公式，动态调整搜索位置；二是利用线性递减惯性权重策略，提升粒子寻优效率；三是引入群体适应度方差策略，判断粒子聚集程度，将两种惯性权重策略动态结合，动态提升全局和局部搜索的能力。

1  粒子群优化算法

PSO算法是一种群体智能搜索算法。该算法首先在n维解空间中，初始化由m个粒子构成的种群，m表示群体规模，每一个粒子的位置代表一个可能的解，同时也决定着由目标函数计算的适应值，通过适应值大小即可判断解的优劣。在每次迭代中，粒子通过适应值大小找到自身最优解（个体极值pbest）和整个种群的最优解（全局极值gbest）来更新速度和位置。PSO算法数学描述如下：

第i个粒子的位置表示为n维的向量Xi = （xi1， xi2， …， xin）T，速度表示為n维的向量Vi = （vi1， vi2， …， vin）T。第i个粒子搜索到最优位置为Pi = （ pi1， pi2， …， pin）T，整个群体搜索到最优位置为Gi = （ gi1，gi2， …， gin）T。粒子按照式（1）和式（2）对自身的速度和位置变量进行更新：

式中，i = 1，2，3，…，n表示粒子数量；k = 1，2，…，n表示当前迭代次数；d表示搜索空间的维分量；ω表示惯性权重系数；c1，c2表示加速常数；r1，r2表示随机数，其值是在（0，1）之间； 表示粒子i在第d维的个体极值位置； 表示群体在第d维的全局极值位置。

2  改进惯性权重的粒子群优化算法

2.1  Sigmoid函数

Sigmoid的表达式为：

Sigmoid函数的定义域为（-∞，+∞），值域为（-1，1），在定义域内为连续光滑，且在0.5处为中心对称，并且越靠近x = 0的取值斜率越大。函数图形如图1所示。

2.2  群体适应度方差策略

设粒子数为N，群体适应度方差σ2的计算方式如下：

其中，fi表示第i个粒子的当前适应度值，favg表示当前种群的平均适应度值，f表示归一化因子。

群体适应度方差反映了种群的收敛程度，σ2越小，种群中粒子的收敛程度越高。本文为σ2设定一个阈值γ，当σ2小于该阈值时，判定粒子高度收敛，此时对粒子进行扰动，驱动粒子继续搜索。为了避免扰动处于全局最优状态的粒子，对粒子按适应值排序匹配扰动强度，适应值越好的粒子对应的扰动强度就越小，适应值越差的粒子对应的扰动强度越大。

2.3  自适应惯性权重策略

为了提高粒子的收敛性能和避免粒子陷入局部最优，Shi等[8]首次提出了惯性权重的概念，将惯性权重引入速度更新公式中，并提出典型的线性递减策略，其计算式为：

其中，T表示粒子当前迭代次数，Tmax表示粒子最大迭代次数。

算法在搜索初期惯性權重较大，有利于全局探索，但不易得到精确解，而在搜索后期惯性权重较小，有利于局部挖掘，但容易陷入局部最优。

因此，为了提升算法搜索性能，增强算法跳出局部最优的能力，本文在线性递减策略的基础上，利用Sigmoid函数非线性递增且无限趋近于定值的特点，构造一种新的惯性权重组合更新公式，如式（6）、式（7）所示：

其中，Rmax表示Sigmoid函数的x轴的界限值，此处取Rmax = 10；δ2表示群体适应度方差；γ表示方差阈值，此处取0.1；ωmax和ωmin表示惯性权重上下限值；T表示当前迭代次数，Tmax表示最大迭代次数。

具体转换过程为：当δ2≤γ（γ表示群体适应度方差阈值）时，则执行惯性权重更新公式转换操作。

从公式可以看出，在种群进入高度收敛阶段之前，粒子初期会大范围的在解空间搜寻最优解，增加找到全局最优的可能性。通过δ2判断种群开始进入高度收敛阶段时，此时粒子群已搜寻到较优解。惯性权重将按照粒子适应值大小自适应调节，对于适应值较差的粒子，惯性权重匹配为较大值，能驱使粒子飞向更远的解空间搜索最优解，提升了跳出局部最优的能力；而对于适应值较优的粒子，惯性权重匹配较小值，驱使粒子在局部范围挖掘最优解，提升了粒子局部搜索能力。

Sigmoid函数变化如图1所示，惯性权重变化如图2所示。

从图中可以看出，粒子惯性权重先线性递减更新，在解空间寻优；当粒子收敛程度达到设定的阈值时，粒子惯性权重采用非线性递减策略更新，在解空间搜索和局部精细搜索，增强跳出局部最优能力。

2.4  算法步骤

CWPSO算法的执行步骤如下：

1）算法参数初始化。包括种群规模N，学习因子c，迭代次数T，最大最小惯性权重ωmax和ωmin，收敛阈值γ。

2）随机产生N个粒子的速度和位置作为初始种群。

3）确定初始种群的个体最优和全局最优。

4）判断δ2是否达到收敛阈值γ。若δ2＞γ，则根据式（7）调节惯性权重大小；若δ2≤γ，则根据式（6）调节惯性权重大小。

5）根据式（1）更新粒子的速度、式（2）更新粒子的位置。

6）计算粒子适应值，并进行记录。

7）更新个体最优和全局最优。

8）判断算法是否达到终止条件，达到条件则导出最优解；否则，返回继续执行步骤4。

3  数值仿真分析

3.1  测试函数

为了验证本文的算法的有效性，选取常用的2个标准测试函数进行数值仿真，其中f1为单峰值函数，f2为多峰值函数。函数相关属性如表1所示。

3.2 群体适应度方差δ2选取试验

在本文的改进粒子群算法中引入群体适应度方差公式，需要给群体适应度方差δ2赋予一个参数值，算法需要根据给定的群体适应度方差δ2的参数值进行自适应地搜索调整，因为当群体适应度方差δ2取不同参数值时，本文改进的优化算法会得到不同的寻优结果。为了确定群体适应度方差δ2的最优取值，本文选取表1中单峰函数Sphere和多峰函数Rastigrin两个标准测试函数进行测试。为了使测试更为准确，测试方式选择本文改进算法重复运行50次，测试实验软件为Matlab 2016a，最终取所有测试结果中的最优值作为比较结果。群体适应度方差δ2参数最优取值的具体测试结果如表2所示。

由表2的实验结果可知，在单峰函数Sphere的数值实验中，群体适应度方差δ2分别取0.1、0.2、0.3时，本文算法搜索的到最优解不同，且随着参数取值变大而变大，此时δ2最优参数取值为0.1；在多峰函数Rastigrin的数值实验中，群体适应度方差δ2分别取0.1、0.2、0.3时，本文算法搜索的到最优解也不同，虽然最优解差别没有太大，但依然随着参数取值变大而变大，此时δ2最优参数取值仍然为0.1。通过以上两组测试函数的实验表明，无论在单峰函数Sphere还是在多峰函数Rastigrin中，本文改进算法由于群体适应度方差δ2取值不同，在单峰函数Sphere和多峰函数Rastigrin上搜索到的最优值结果就会不同，且当本文改进算法的群体适应度方差δ2 = 0.1时，本文改进算法的整体搜索性能最优。

3.3  对比算法

为了进一步验证改进算法的有效性，选取基本的粒子群算法（PSO）、线性递减惯性权重粒子群算法（LWPSO）与本文算法（CWPSO）作比较。单峰测试函数Sphere和多峰测试函数Rastigrin的维数D = 10，粒子数N = 40，迭代次数1 000次，独立运行50次，仿真实验软件为Matlab 2016a。算法参数的选取如表3所示。

3.4  算法性能对比分析

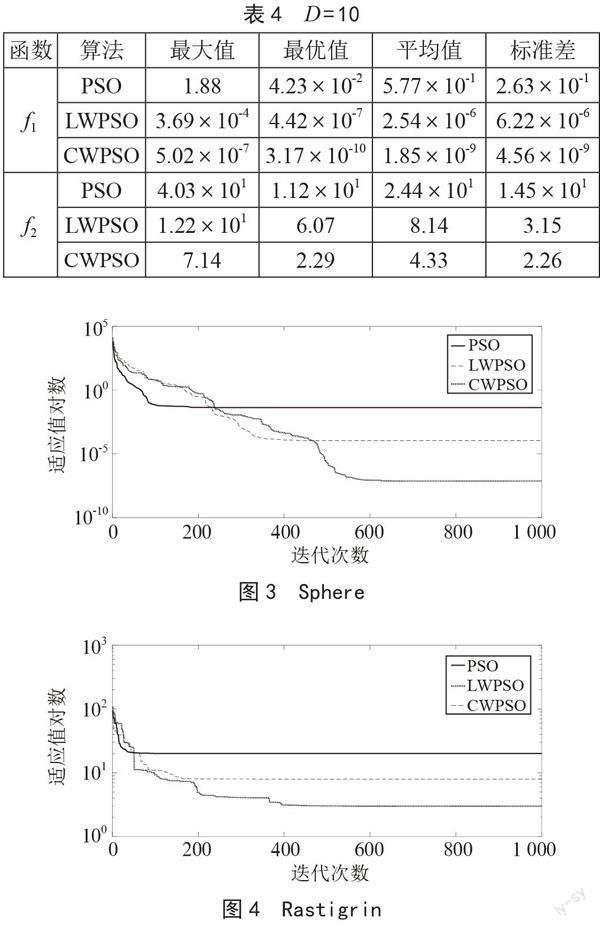
由表4可知，在维数D = 10的情况下，在单峰函数f1和多峰函数f2寻优中，本文算法（CWPSO）搜索到的最优解均优于PSO和LWPSO算法，说明CWPSO算法性能得到改善，寻优能力增强，证明了本文改进策略的有效性。

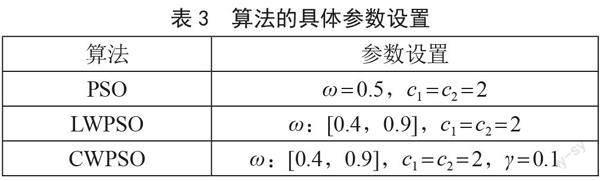
由图3可知，在迭代中期，CWPSO算法通过群体适应度方差策略判断粒子陷入早熟，开始自适应调整惯性权重，帮助粒子跳出局部最优，搜寻更优解。由图4可知，多峰函数下粒子搜索范围缩小速度要快于图3，PSO最先陷入局部最优，LWPSO次之，而CWPSO依然反复在解空间搜索最优解，寻优性能提高，尋优结果优于PSO和LWPSO。

4  结  论

本文提出了一种改进惯性权重策略的PSO算法，即CWPSO算法。所提算法采用群体适应度方差策略来判断粒子群体收敛程度，使得粒子能够自适应地调整搜索方向，同时结合Sigmoid函数，利用Sigmoid函数的无限趋近特性进一步来提升粒子自适应性能。通过群体适应度方差与Sigmoid函数结合策略，算法增强了粒子种群的多样性，提高了粒子群搜索解空间的解搜索能力。通过单峰测试函数与多峰测试函数分别进行的数值实验表明，本文提出的CWPSO算法提升寻优性能有效，提高了算法的求解能力。

参考文献：

[1] KENNEDY J，EBERHART R C. Particle swarm optimization [C]//Proceedings of IEEE International Conference on Neural Networks.Piscataway：IEEE，1995：1492-1498.

[2] 方春恩，唐小雨，李伟，等.基于多策略粒子群算法的500 kV直流断路器用快速机械开关优化设计 [J].高压电器，2022，58（1）：79-88.

[3] 帅茂杭，熊国江，胡晓，等.基于改进多目标骨干粒子群算法的电力系统环境经济调度 [J].控制与决策，2022，37（4）：997-1004.

[4] 林安，张磊，陈国兵，等.基于改进粒子群算法的船用汽轮机DEH智能控制优化 [J].舰船科学技术，2022，44（13）：126-131.

[5] 李二超，高振磊.改进粒子速度和位置更新公式的粒子群优化算法 [J].南京师大学报：自然科学版，2022，45（1）：118-126.

[6] 周利军，彭卫，邹芳，等.自适应变异粒子群算法 [J].计算机工程与应用，2016，52（7）：50-55+149.

[7] 闫群民，马瑞卿，马永翔，等.一种自适应模拟退火粒子群优化算法 [J].西安电子科技大学学报，2021，48（4）：120-127.

[8] SHI Y，EBERHART R. A modified particle swarm optimizer [C]//1998 IEEE international conference on evolutionary computation proceedings.IEEE world congress on computational intelligence （Cat. No. 98TH8360）.IEEE，1998：69-73.

[9] 薛文，苏宏升.基于分群策略的混沌粒子群优化算法 [J].计算机工程与设计，2019，40（2）：443-448.

作者简介：薛文（1989—），男，汉族，黑龙江哈尔滨人，助教，硕士，研究方向：电力系统稳定与控制。

收稿日期：2022-11-23